应急物资配送网络弹性设计模型研究*
2018-11-01杨家其王海燕呼格吉勒
葛 雪 杨家其 王海燕 呼格吉勒
(武汉理工大学交通学院1) 武汉 430063) (宁波工程学院经济与管理学院2) 宁波 315211)
0 引 言
应急物流具有复杂性、多变性、突发性、破坏性、持续性和连锁性等特点,其运行过程存在极高的风险和脆弱性,极容易发生供应延迟甚至断链事件.
目前将经典的资源选址与资源配置方法运用到应急物流领域的研究已经比较成熟,但针对应急物流运输网络本身运行风险的相关研究还比较少.彭春等[1]在考虑供需不确定的基础上对应急物资供应网络进行鲁棒优化.王海军等[2]采用模糊数的方法来描述应急物资供需的不确定性,构建了多商品、多式联运、多阶段及多目标的应急物流选址-分配模型.Tofighi等[3-4]综合考虑了灾后供需的不确定性和交通可得性的不确定性,对应急运输网络进行构建.陈春霞[5]构建了单一起点和单一终点的应急物流网络,并基于复杂网络理论对应急物流网络的抗毁性进行了研究.李健等[6]采用路网节点可靠度来对网络可靠性进行评估.以上文献分别从柔性、鲁棒性、抗毁性及可靠性等角度对应急物资运输网络的风险问题进行研究.事实上,构建弹性被认为是克服脆弱性的一种有效途径[7-8].Katherine Pasteur[9]认为社会弹性是指一种系统(社区或社会)面对灾难的抵抗、吸收和应付的能力.刘希龙[10]采用供应网络在发生失效且恢复后的供应量损失来量化供应网络的弹性,并构建线性规划模型对供应链的弹性进行优化.Falasca等[11]将弹性的理念预嵌到供应链的设计阶段,并基于此开发了一套采用供应链网络的密度,复杂性和节点临界这三项表征值来评估供应链抗灾能力的方法.Torabi 等[12]提出系统的弹性包含了“适应性”、“稳定性”和“可靠性”,并对运输网络弹性进行量化分析.但这些文献的研究对象是常规供应网络.应急物资配送网络具有高时效性、弱经济性、高风险性,并往往呈现三级网络结构,与常规网络在模型的构建上有很大的区别.目前从弹性角度研究应急物流运输网络风险的文献很少.吴依伟等[13]对应急物流网络弹性进行探索,但他并未对网络弹性测度进行深入探讨.
基于此,构建弹性是克服应急物流网络脆弱性、减小应急物流运性风险的有效手段.本文结合弹性的内涵,提炼出应急网络的弹性提升策略,在物资储备点、集配点到受灾地的三级应急配送网络的基础上,考虑交通阻断的概率,构建多种运输方式、多目标、基于混合整数规划的应急物资配送网络弹性设计模型.
1 应急物资配送网络基本模型
1.1 问题描述
突发事件尤其是大规模突发事件影响范围广、影响强度大、所需物资种类多,就近的应急物资储备点难以满足灾区对应急物资的巨大需求,因而通常高需要进行跨区域调度物资.现行做法往往是在离受灾区较近的地点建立若干个应急物资集配点,实现应急物资的汇集再分配,形成三级配送网络结构,见图1.同时,为了快速响应物资需求,现实中往往综合使用多种运输方式.

图1 应急物资配送网络结构图
基本模型的构建将基于以上情况,考虑灾区附近路段被破坏的可能性,以及存储量约束、道路容量约束、运输方式约束,以应急物资配送运输时间最小、应急物资供应率最大为优化目标.
1.2 模型假设
建立本模型需要考虑以下几个假设条件.
假设1灾害发生初期是救灾黄金时期,因此本模型仅考虑首次运输(单次运输);同时应急指令一旦下达,所有应急单位在第一时间开展救援行动,因此假设所有物资从应急物资储备点同时出发.
假设2外援、捐赠的供应是不确定的,且在灾害发生初期也不可能迅速送达,因此假设应急物资全部来自应急物资储备点.
假设3大型应急储备中心分布分散,出于对运输大批量和长距离的考虑,应急储备点到应急集配点可考虑铁路和公路两种运输方式,且不考虑此项运输路段受阻;通往灾区的道路被损坏可能性大,应急物资集配点到灾区考虑公路和航空两种运输方式,同时考虑路段受阻情况.
假设4为了问题的简化,仅考虑一种物资,且不计换装时间.
1.3 符号说明
已知参数I为应急储备点集合,I={1,2,…,i,…};J为应急集配点集合,J={1,2,…,j,…};Si为应急储备点i的存储量;dis1ij为从i地到j地的运输距离;dis2j为从j地到受灾地的运输距离;q为灾区对应急物资的需求量;vt为铁路运输速度;vh为航空运输速度;vg为公路运输速度;cap1tij,cap1gij为i到j地的铁路公路容量;cap2gj,cap2hj为j地到灾区的公路、航空容量;p2gj为救援点j运往受灾区的公路完好的概率;p2hj救援点j运往受灾区的航空完好的概率.
决策变量xij为从应急储备点i运往应急集配点j的货量;yj为从应急集配点j运往受灾区的货量aij:应急储备点i运往应急集配点j的线路是否被选中.若选中,则aij=1;反之,则aij=0;cj为应急集配点j是否被选中.mod1gij为0-1变量,从i运往j采用铁路运输还是公路运输.采用公路运输方式,取1;否则取0;mod1tij为0-1变量,从i运往j采用铁路运输还是公路运输.采用铁路运输方式,取1;否则取0.
1.4 模型构建
应急调运具有弱经济性,其根本目标是在尽可能短的时间内,尽可能多地满足受灾点的应急物资需求.在这里,由于所有物资同时出发,网络运输时间即最慢线路的运输时间;由于路段可能发生中断,这里供应率采用期望值来计算,因此,目标函数表示为
minTimemax
(1)
(2)
式中:


且有Eyj=yj·(p2gj·mod2gj+p2hj·mod2hj)
每个物资集配点的物资进入量等于流出量,即有
·aij=yj,∀j∈J
(3)
未被选中的救援点,没有物资流进或流出,即有
·aij≤α·bj
∀j∈J,α为一无穷大正整数.
(4)
对受灾区的供给量不大于其需求,即有
·cj≤q
(5)
应急储备库发出的物资应不大于其存储量,即有
·aij≤si,∀i∈I
(6)
运输量会受到路线容量的限制,即有
每条路线仅选择一种运输方式,即有
mod1gij+mod1tij=aij,∀i∈I,j∈J
(8)
mod2gj+mod2hj=cj,∀j∈J
(9)
综上所述,基本模型的目标函数为式(1)~(2);约束条件为式(3)~(9).
2 弹性设计模型与求解
2.1 弹性设计模型
本文构建弹性设计模型的方法是在基本模型中引入弹性提升策略.弹性网络的物理特点包括:“设计与需求相匹配”“并行(平行)路径”“更短的供应链”“供应链的形状(并联优于串联)”“高库存”“富余的容量”“高度的敏捷性”.应急物资配送网络本身即具备灵活性强、短链、敏捷性强等特点,因此,本节在基本模型的基础上,主要采用“增加并联线路”“高库存”以及“富余的容量”三项策略,来构建应急网络弹性设计模型.
策略1通过增加备选的物资配送中心来增加并联线路 应急物资配送呈现“应急储备点→应急集配点→受灾地”的三级网络结构.因应急集配点往往就近设立,受到灾害影响的可能性较大,容易发生失效而产生链路中断.提前设立备选的应急集配点,能及时恢复网络运行.
增加决策变量 令可供增加的应急集配点集合为N,应急集配点的备选集合则为J+N.
在这种情况下,式(4)、式(8)~(9)分别变为
·aij≤α·bj,∀j∈J+N,
α为一无穷大正整数.
(10)
mod1gij+mod1tij=aij,∀i∈I,j∈J+N
(11)
mod2gj+mod2hj=cj,∀j∈J+N
(12)

在这种情况下,式(6)变为

(13)
策略3建立线路容量的冗余 路线容量的冗余,使得巨大的物资需求突发产生以后,能迅速地对应急物资、交通工具进行疏散,从而提高应急网络的弹性.增加决策变量:令道路、航路容量分别增加cap′2gj、cap′2hj.
在这种情况下,式(7)变为:
(14)
在实践中,弹性设计需要对成本与风险进行综合权衡,因此,考虑各项成本约束和资源限制,综合各项弹性提升策略对应急物资配送网络进行设计十分有必要.增加以下参数:弹性设计经费预算fund;物资储备点i每增加一个单位的存储量,成本增加ei;道路、航路容量每增加一个单位,成本分别增加f2gj、f2hj;物资集配点每增加一个,建设成本增加gn.
弹性设计方案的实施受经费预算的限制,即有

(15)
综上所述,弹性设计模型的目标函数即为基本模型的式(1)、(2);约束条件为式(3)、式(5)、式(10)~(15).
2.2 求解算法
针对上述双目标规划模型,设计以下求解算法.
步骤1去掉原模型中目标函数(1)并求解,获得针对目标函数(2)的最优解,设该值为opt2.
步骤2去掉原模型中目标函数(2),加入约束条件(16)并求解,即获得原目标函数的最优决策方案.
≥α·opt2 , 0≤α≤1
(16)
这里需要对以下命题进行证明.
命题依据以上算法求解得到的解为原模型的弱有效解.
证明采用反证法.

所以,该命题成立.
3 算例分析
3.1 算例描述
A县是自然灾害频发地区.假设在某次大型灾害后,A县对某种物资的需求量为625份.应急指挥中心紧急选定从6个城市的应急物资储备点调配物资,选定靠近灾区的3个县城作为应急物资集配点.该物资在6个物资储备点的储存量见表1.

表1 应急物资储备情况 份
通过Google地图软件获取了应急物资集配点与应急集配点之间、应急集配点与灾区之间的里程,见表2~3.
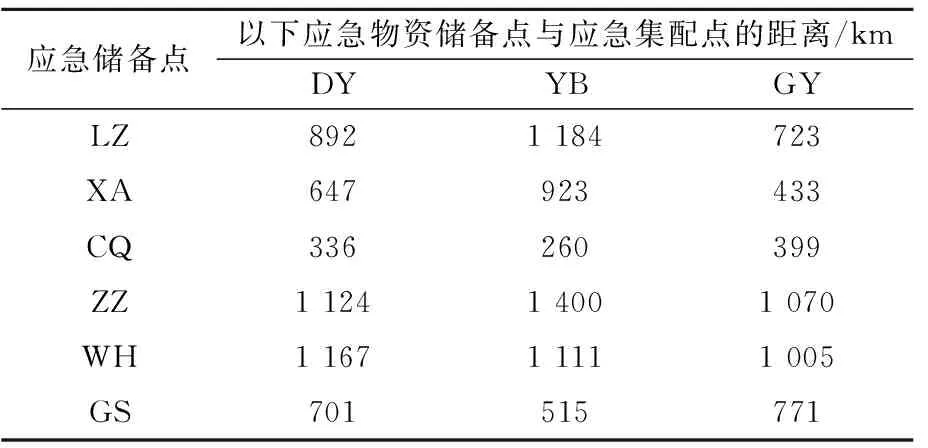
表2 应急储备点与应急集配点距离矩阵

表3 应急集配点与灾区距离矩阵
公路运输的道路容量统一设为200个单位;航空运输的道路容量统一设为80个单位;铁路运输的道路容量500个单位.航空运输的速度为600 km/h;公路运输的速度为80 km/h;铁路运输的速度为100 km/h.三个应急配送中心通往灾区的道路能正常运行的概率分别为0.7,0.6,0.6.
弹性构建的总经费为95个单位;ei统一设为0.2个单位;f2gj统一设为0.4个单位,本案例假设不具备航路扩容的能力,f2hj设为无穷大;可供增加的应急配送中心为城市LS,其建设成本gn为50个单位,LS距离6个应急储备中心的距离分别为1 100,870 ,310 ,1 360,1 230 和830 km;距离灾区的距离为270 km;LS到灾区的道路能正常运行的概率为0.7.
3.2 算例分析
1) α=1时实验结果 此时求得的供应率为最大值.求解得出供应率为60.8%,运输时间为19.8 h.对应的应急物资配送网络的运输组织情况见图2.两个阶段的运输尽可能采用铁路和公路这类容量较大但速度较慢的方式,此时最长运输线路为“ZZ→YB→受灾地”.

图2 α=1时基本模型运输组织图
弹性设计模型中,令α=1,求解得出此时供应率为77.7%,运输时间为18.8 h.对应的应急物流运输网络的运输组织情况见图3.

图3 α=1时弹性设计模型运输组织图
相比基本模型,由于多出一个配送中心,且瓶颈路线的道路容量有了一定程度增加,部分路段的运输采用了航空运输,从而有效地减小运输时间.此时最长运输线路为“ZZ→YB→受灾地”.
对比图2~3可知,经过弹性设计以后的供应率得到了一定程度的提升,且运输时间得以减小.
2) 多次试验结果 分别对α取不同值,使基本模型中的供应率分别大于等于30.0%,50.0%,60.0%,最大值,使弹性设计模型的供应率分别大于等于30.0%,50.0%,60.0%,70.0%、最大值,将实验结果绘制成散点图,见图4.从“供应率”和“运输时间”两个维度来看,采用弹性设计的应急物资配送网络优化结果明显优于不使用弹性策略时的情况.
分别记录各项优化结果下弹性设计模型的决策变量取值,见表4.结果显示在不同的最优结果组合中,三项弹性策略发挥了不同程度的作用.其中,第1组仅使用策略2;第2组综合使用策略1、策略2和策略3;第3组综合使用策略1和策略2;第4组综合使用策略1、策略2和策略3;第5组综合使用策略1和策略3.

图4 应急物资配送网络弹性设计效果散点图
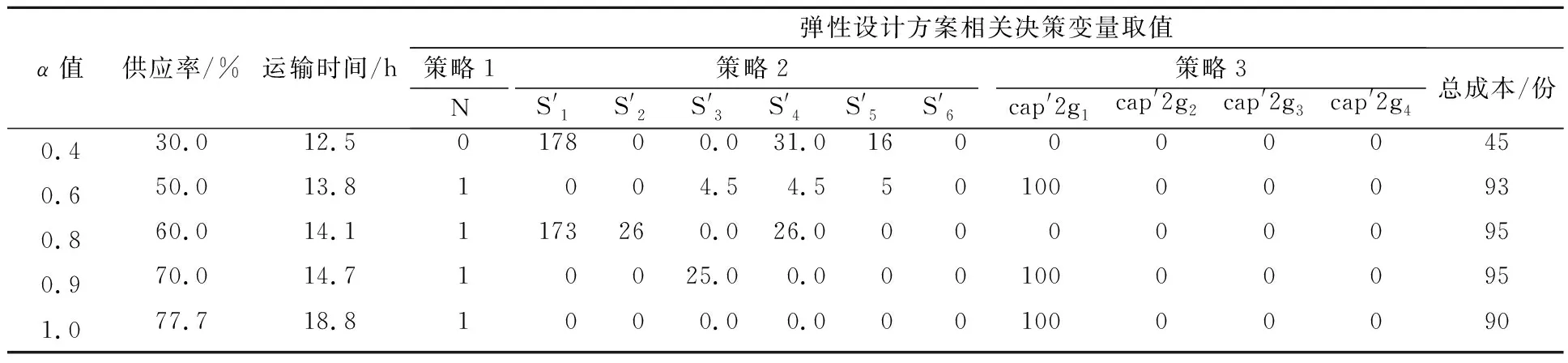
表4 不同α值下的应急物资配送网络弹性设计方案α值供应率运输时间
4 结 束 语
本文提炼了应急网络的弹性提升策略,并考虑交通阻断的概率,以运输时间最短、物资供应率最大为目标,构建了多种运输方式、多目标、基于混合整数规划的应急物资配送网络弹性设计模型.并采用赋权法将双目标转化为单目标,以此来增加决策的柔性.算例通过改变赋权值的大小进行了多次实验,充分验证了本模型有效性.研究表明,该模型能提升应急物资配送网络的物资供应期望值,同时减小运输时间,从而大大提升了网络的弹性.在今后的研究中,将进一步研究灾区应急需求不确定情形下的网络弹性问题,并采用大规模的算例进行验证,进一步提高模型的有效性,从而为应急物资配送网络风险防范决策提供更充分更科学依据.
