考虑原子纵向位移单原子链横向振动压电控制
2018-11-01刘灿昌巩庆梅马驰骋周继磊姜瑞瑞周长城
刘灿昌, 巩庆梅, 马驰骋, 周继磊, 姜瑞瑞, 周长城
(山东理工大学 交通与车辆工程学院,山东 淄博 255049)
近年来,随着电子材料制造由二维降至一维,单原子链作为一种理想的一维导体,具有亚纳米尺寸、量子化电导、高长宽比和弹性模量、特殊的光学和电磁响应等特点,广泛应用于光学和电子学等纳米器件的制造。单原子链还具有终极大的比表面积、电导开关和负微分电阻等特性[1-2],是纳米电子器件的重要组成部分[3]。
高频纳电子机械系统(Nano-Electromechanical System,NEMS)振荡器的制备是十余年来极为活跃的研究课题。Rouke课题组[4]制备出超过十亿赫兹的NEMS振荡器。Chaste等[5]制成的碳纳米管谐振器基频达到了千兆赫兹。随着碳纳米管等新结构出现,碳纳米管振荡器的基频得到较大提高,由于碳纳米管在生长上无法控制,难以批量制备,阻碍了在实际电路中的应用[6]。目前,高频振荡器的核心部件纳米结构因存在尺寸效应、量子效应[7]和材料缺陷等原因限制了振荡器性能的提高,制约电子技术的发展,因而,迫切需要一种新结构以满足高基频、高品质因数的需要。
近几年来,科学工作者提出了许多单原子链制造方法并展开单原子链相关特性的研究。Ohnishi等[8]首先制造了金单原子链。通过移除石墨烯纳米带中的碳原子可以得到线性原子链[9-10]。直接利用电弧或用含有氢气、液氮和氦气的电弧可以在多层碳纳米管内合成碳链[11-12]。第一性原理已经广泛应用于单原子链的电导特性、电子输运性能、吸附性能的研究[13-15]。Yu[16]利用递归关系方法研究了含有杂质双原子链动量自相关函数。解忧等研究了扶手椅型石墨烯纳米带吸附金属磁性Ni和非磁性Cu 单原子链的结构、电子性质和磁性[17]。华军等[18]利用分子动力学方法建立了硅离子辐照石墨烯和辐照后拉伸的数值模型。
单原子链的振动研究引起了科技界的普遍重视。Hizhnyakov等[19]利用解析和数值方法研究垂直于单原子链方向和垂直石墨烯表面的非谐横向振动。Glushko等[20]运用矩阵转置法研究了单原子链色散与电子密度分布状态的关系。Kosevich等[21]对含有四阶空间导数的微分方程的适用条件进行了分析,描述了原子链的长波振动。科学家们在具有螺旋结构的单原子锰链中发现了法诺共振现象[22]。Hoogeboom等[23]研究了单原子颗粒链离散呼吸子的存在、稳定性与动态力学性能,并研制出了一整套系统性的检测方法。然而,以上研究基于第一性原理的分子动力学模拟,计算复杂,计算量大,难以应用于多原子结构的计算。因此,在单原子链制作技术不断提高的今天,亟须加强对单原子链横向振动的理论研究。
本文研究了考虑原子纵向位移时单原子链的横向振动,假设其横向振动模态为弦的振动模态,运用牛顿第二定律建立单原子链横向振动的动力学方程,研究了固有角频率与纳米线的压电控制电压、长度之间的关系。通过数值迭代法,结合单原子链的边界条件与对称性计算得到原子的纵向振动位置坐标,并给出单原子链纳米线的固有角频率的计算公式和压电控制电压的量子极限值。
1 单原子链的自由振动
单原子链纳米线横向振动压电控制装置包括单原子链纳米线和压电控制电路。如图1所示,压电控制电路由上压电块和下压电块串联组成,压电块上表面和下表面镀有一层金薄膜,通过导线与控制电压源连接,组成闭合控制电路。调节控制电压源的控制电压,可以改变压电块轴向位移,单原子链沿着轴向位移变化改变轴向力的大小,实现轴向力的控制。

图1 单原子链示意图Fig.1 Monatomic chains diagram
单原子链中的原子由化学键连接,化学键的长度,即相邻原子间的间距为非固定值,原子链横向振动时其所有原子整体振动,因而可将单原子链的振动模态视为弦的横向振动模态。纳米线的热振动振幅远远小于其横向振动振幅,因此可忽略不计。
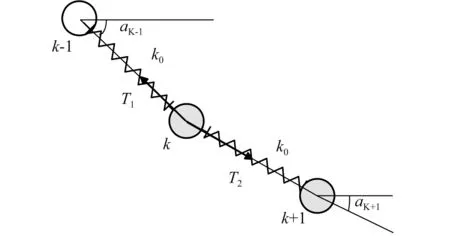
图2 原子的受力分析Fig.2 Forces analysis of the atoms
单原子链结构具有连续性和离散性的特征,动力学建模较为复杂。为简化单原子链振动模型,提出如下假设:
(1) 当单原子链平衡时所有原子处于一条直线上。
(2) 单原子链振动为纳米线的振动,其横向振动模型可视为弦振动模态。本文还假设单原子链的横向振动为简谐振动,单原子链原子具有相同的振动特征,即具有相同的固有角频率。
(3) 单原子链纳米线相邻原子间的弹性刚度为固定常数,忽略原子间的弯曲刚度。
单原子链由N+1个原子组成,单个原子的质量为mk(k为原子的编号),单原子链纳米线的横向振动挠度可表示为
(1)
式中:wk表示单原子链纳米线中第k个原子的振动挠度;qki为第k个原子横向振动时的时域函数;i是纳米线振动模态的模态数;xk为第k个原子的位置坐标。t为时间函数;l则是单原子链纳米线的长度。不失一般性,先研究单原子链纳米线第i阶模态振动特性,其它模态振动特性采取类似的研究方法。原子受力如图2所示。
由牛顿第二定律可以得出
T2cosαk+1-T1cosαk-1=0
(2)
(3)

T2-T1=0
(4)
(5)
单原子链横向振动时,不同原子所在位置的转角不同,导致受力不同,原子间距离因力的大小改变出现变化,因而研究单原子链横向振动时,需要考虑原子位置坐标的变化。两个相邻原子间的挠度差值可写为
(6)
(7)
第k-1与第k+1个原子的时域函数可写为
(8)
(9)
将等式(8)、(9)与(1)代入式(5)中,得到单原子链纳米线的振动方程
(10)

由于单原子链横向振动原子的固有角频率为正值,其平方根表达式为
(11)
压电控制器轴向力可以表示为
(12)
压电控制单原子链纳米线横向振动固有角频率可以表示为
(13)
式中:L为压电片的长度;K为原子间力常数;d为压电片的厚度;d31为压电片的压电常数;n为单原子链原子间隔数;U为压电块控制电压。
2 单原子链纵向位移计算
根据离散体的变形协调原则可知单原子链做横向振动时所有原子具有相同的固有角频率,因而可以令相邻原子的固有角频率相等,得到
ωk=ωk+1,k=1,2,…,N-2
(14)

考虑单原子链的边界条件和对称条件,未知变量数等于方程组方程的个数,非线性方程组是可解的。
由于方程组是非线性方程组,因此难以得到方程组的解析解。通过牛顿迭代法可以计算出方程组的数值解。振动频率非线性方程组可写为
(15)
式中:Z=[z1…z(N-1)/2z(N+1)/2zN-1]T(N为奇数),Z=[z1…zN/2zN/2+dzN-1]T(N为偶数)。 振动频率非线性方程组迭代计算公式为
Z(j+1)=Z(j)-(F′(Z(j)))-1F(Z(j))
(16)
式中: (F′(Z(j)))-1是导数矩阵F(Z)中的逆矩阵。
3 振动量子极限分析
近年来量子电子机械系统(Quantum-Electro Mechanical Systems, QEMS)成为研究的热点问题,NEMS和QEMS一般按照无量纲“热占有数”划分
(17)

(18)
若应力小于或等于ULimit, 单原子链振动则属于NEMS范畴;否则,则应考虑单原子链振动的量子效应。将振动模型量子化,其量子化能量可以表示
(19)
式中:M为单原子链振动固有角频率占有因数。
4 算例分析与讨论
本文以单原子链纳米线横向振动为研究实例进行分析。单原子链两相邻碳原子的间距r0为1.282×10-10m,两原子间键力刚度K为642 N/m,单原子链长度l=(N-1)(r0+T/K),碳原子质量为1.993×10-26kg[24]。算例中,奇数单原子链的原子个数分别为7,9和11,偶数单原子链的原子个数分别为8,10和12,研究第3个原子振动频率。以下算例仅以单原子链一阶模态振动为例展开分析。
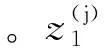
碳单原子链纳米线谐振动轴向力控制电压量子极限随温度的变化图像如图4所示。压电块长度为10 nm,厚度为2 nm,压电常数为d31=123×10-12C/N。
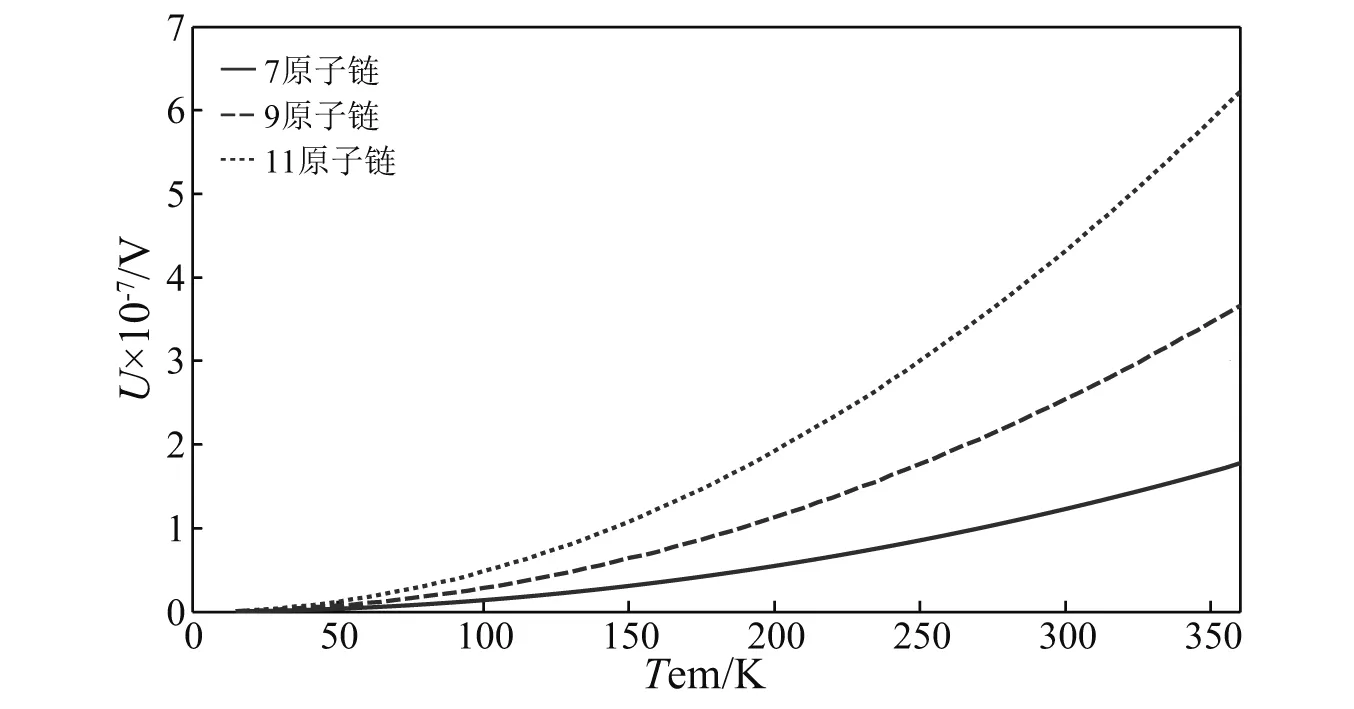
图4 碳单原子链控制电压量子极限值随温度变化图Fig.4 Axial force control quantum limitation voltage changing with temperature
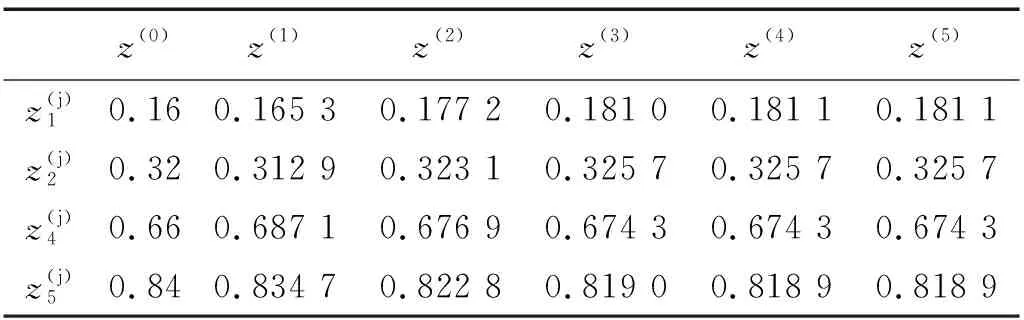
表1 原子个数为7时的非线性方程组的迭代解Tab.1 Iterative solutions to the nonlinear equation groupfor a seven-atom chain
由图4可知,当单原子链纳米线长度一定时,其谐振动的轴向力控制电压量子极限随着温度的升高而增大,温度越高,轴向力控制电压量子极限值越大。当温度一定时,单原子链纳米线谐振动的轴向力控制电压量子极限随着单原子链长度的变小而变小,长度越小,轴向力控制电压量子极限值越小。
图5表示碳单原子链固有角频率与轴向力控制电压的变化关系图,图中单原子链原子个数分别为7,9,11。由图5可知,原子的轴向力控制电压对固有角频率的变化作用明显。当单原子链原子个数一定时,固有角频率随轴向力控制电压的增大而增大。当轴向力控制电压不变时,固有角频率的固有值则随原子链长度的缩短而增加。因此,通过改变单原子链纳米线原子个数和轴向力控制电压可以实现固有角频率控制。当单原子链谐振器受到的激励频率等于纳米梁固有角频率时,谐振器会发生共振,此时激励频率是共振频率。图6表示单原子链一阶振动模态共振频率与轴向力控制电压变化关系图,图中原子个数分别为7、9、11。共振频率随轴向力控制电压的增大而增大。当轴向力控制电压为常数时,共振频率的数值随原子链长度的缩短而增加。
图7与图8为碳单原子链固有角频率与共振频率与轴向力控制电压的变化关系示意图,单原子链原子个数分别为8,10与12。由图可知,固有角频率与共振频率的数值则随原子链长度的缩短而增加。当单原子链长度为常数时,其固有角频率与共振频率随纳米线轴向力控制电压的增加而增加。因此,通过改变单原子链纳米线长度和轴向力控制电压可以改变系统固有角频率与共振频率。
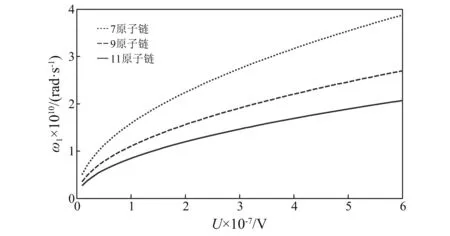
图5 碳单原子链固有角频率与轴向力控制电压的关系图Fig.5 Variation of the natural angular frequency of the carbon monatomic chain changing with control voltage
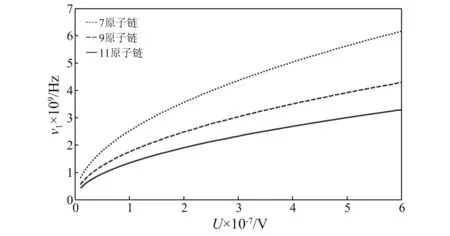
图6 碳单原子链共振频率与轴向力控制电压变化关系图Fig.6 Variation of the resonant frequency of the carbon mo-natomic chain changing with control voltage

图7 碳单原子链固有角频率随轴向力控制电压变化图Fig.7 Variation of the natural angular frequency of the carbon monatomic chain changing with control voltage

图8 碳单原子链共振频率随轴向力控制电压的变化图Fig.8 Variation of the resonant frequency of the carbon monatomic chain changing with control voltage
碳原子链的键破断强度为2.6~13.4 nN[25],压电对单原子链轴向控制力的可控范围较大,可通过选定适当的压电控制电压来调谐固有角频率值。利用单原子链纳米线固有角频率随轴向张力改变的特性制造高频谐振器,满足纳机电系统时钟电路、调谐器等对高频信号的需求,将极大推动谐振器技术的发展。
5 结 论
本文基于弦振动理论建立单原子链纳米线的运动方程。通过设定恰当的轴向力控制电压与链长可设计出超高频单原子链谐振器。
运用迭代算法可以求出纳米线原子纵向位移非线性方程组的迭代解,得到纳米线横向振动原子的纵向位置坐标值,迭代算法数值解收敛快。两端固支单原子链纳米线的振动具有对称性。
通过热占有数可以区分NEMS和QEMS,得到量子极限时的压电控制临界电压。单原子链纳米线谐振动的轴向力控制电压量子极限值随着温度的升高而增大,随着单原子链长度的变小而变小。改变环境温度和单原子链的长度可以改变轴向力控制电压量子极限值。
作用于单原子链的轴向力控制电压能改变系统的固有角频率。固有角频率和共振频率随轴向力控制电压的增大而增大,随原子链长度的缩短而增加。通过改变单原子链纳米线原子的轴向力控制电压可以改变结构的振动参数。
