冷弯薄壁型钢-石膏基自流平砂浆组合楼盖基频研究

2018-11-01管宇，石宇，高立

振动与冲击 2018年20期

管宇，石宇，高立

(1．长安大学建筑工程学院，西安 710061； 2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

在正常使用阶段，冷弯薄壁型钢组合楼盖在人行荷载或冲击荷载激励下容易产生振动现象，虽然危及不到结构的安全性能，但涉及人体感受的舒适程度。随着住宅体系对楼盖安全和舒适度要求的提高，组合楼盖的振动性能也对人的日常活动产生重大影响。

冷弯薄壁型钢-石膏基自流平砂浆组合楼盖是采用自攻螺钉将压型钢板与冷弯薄壁型钢楼盖梁、边梁进行连接，并在压型钢板上浇筑石膏基自流平砂浆组成的一种共同受力、协调变形的新型组合楼盖。与舒适度相对较低的OSB板组合楼盖[1-2]和自重较大、施工效率较低的混凝土组合楼盖[3]相比，石膏基自流平砂浆组合楼盖轻质、施工操作简便、成型后表面光洁平整，而且楼面板不会因热胀冷缩而产生开裂、起鼓等现象。为考察冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的振动性能，研究组合楼盖的自振频率，避免该类楼盖发生共振，是首要解决的问题之一。

美国钢结构设计指南[4]规定轻质楼盖自振频率不得小于8 Hz，欧洲抗震规范[5]规定楼板自振频率不得小于9 Hz。我国的《钢结构住宅设计规范》(CECS 261—2009)[6]中规定住宅楼板的自振频率不宜小于8 Hz；《高层民用建筑钢结构技术规程》(JGJ 99—2015)[7]要求组合楼板在永久荷载作用下的自振频率不得小于15 Hz。魏健[8]建议以冷弯薄壁型钢-意杨胶合板组合楼盖的自振频率不小于15 Hz作为舒适度评价标准。周绪红等[9-10]提出对振动性能要求较高的冷弯薄壁型钢-OSB板组合楼盖的自振频率限值取为15 Hz，在正常使用阶段荷载标准组合下，冷弯薄壁型钢-混凝土组合楼盖的自振频率不应小于10 Hz。目前，国内规范对楼盖自振频率的限值并不统一，且自振频率的计算方法也不相同，尚无明确的设计方法和评价标准。

本文对冷弯薄壁型钢-石膏基自流平砂浆组合楼盖足尺模型进行了振动试验，研究钢丝网布置对组合楼盖基频的影响。采用有限元分析方法对组合楼盖基频影响因素进行了模拟分析。在试验研究和有限元分析的基础上，提出预测冷弯薄壁型钢-石膏基自流平砂浆组合楼盖基频的计算方法及设计建议，为编制冷弯薄壁型钢结构体系国家或行业标准提供可靠依据。

1 试验概况

1.1 试件设计

为了研究冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频，试验设计了2个3.6 m×3.6 m的组合楼盖试件，试件编号及加载方式见表1，其中试件CF1的楼面板形式为在压型钢板上浇筑40 mm厚C30石膏基自流平砂浆；试件CF2的楼面板形式为在压型钢板上浇筑40 mm厚C30石膏基自流平砂浆，并设置单层钢丝网，其直径为1.9 mm，网格尺寸为：60 mm×60 mm。试件构造尺寸见图1，图中冷弯薄壁型钢构件具体尺寸见表2，压型钢板截面几何尺寸见图2。

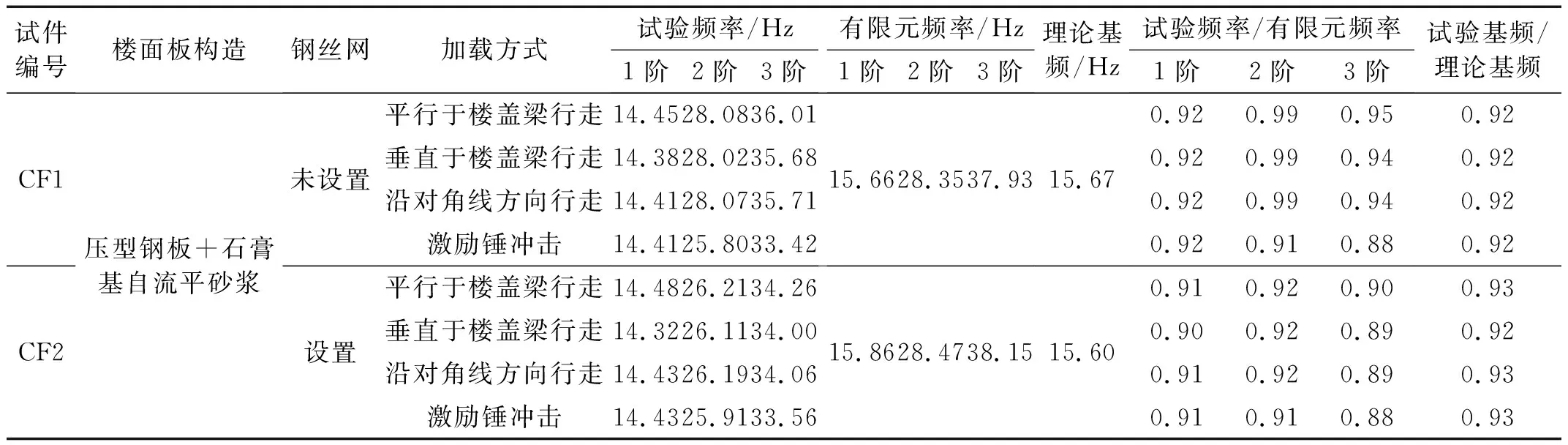
表1 试件参数及频率结果对比Tab.1 Specimen parameters and the comparison of frequency results

(a)试件平面图

(b)1—1剖面图

表2 构件尺寸表Tab.2 Dimension of components

图2 压型钢板截面几何尺寸Fig.2 Dimension of profiled steel sheet

组合楼盖中C形楼盖梁间距为400 mm，在与U形边梁相交部位上下翼缘处采用ST4.8自攻螺钉进行连接。在C形楼盖梁端部设置支座加劲件，长度为240 mm，与楼盖梁、边梁连接构造见图3。为了防止楼盖梁发生侧向扭转，在楼盖梁跨中位置的下翼缘，垂直于梁的方向设置通长的扁钢带拉条，宽度为50 mm，厚度为1 mm，并在边部和中部楼盖梁之间设置3个刚性支撑件，见图3。在楼盖梁上翼缘铺设规格为YX-14-63-820 mm的热镀锌压型钢板(见图2)，厚度为0.75 mm，压型钢板板肋垂直于楼盖梁跨度方向布置。采用ST5.5自攻螺钉连接楼盖梁与压型钢板，周边螺钉间距为125 mm，中间螺钉间距为250 mm。在压型钢板上浇筑设计厚度为40 mm、强度等级为C30的石膏基自流平砂浆，见图3。

图3 构件连接Fig.3 Components connection

1.2 试验材性

冷弯薄壁型钢构件材性试验根据《金属材料拉伸试验第1部分：室温试验方法》(GB/T 228.1—2010)[11]中拉伸试验的规定，测得1.5 mm厚C形楼盖梁的屈服强度为318.4 MPa，抗拉强度为369.6 MPa，弹性模量为2.09×105MPa；0.75 mm厚压型钢板屈服强度为356.3 MPa，抗拉强度为438.6 MPa，弹性模量为2.00×105MPa；1.9 mm直径钢丝屈服强度为376.5 MPa，抗拉强度为470.6 MPa，弹性模量为2.06×105MPa。在浇筑石膏基自流平砂浆时，留置边长为100 mm的立方体和100 mm×100 mm×300 mm棱柱体试块进行同条件养护，测得28 d后石膏基自流平砂浆材性指标,见表3。

表3 石膏基自流平砂浆材性Tab.3 Material property of gypsum based self-leveling mortar

1.3 试验装置及加载方案

试验加载装置见图4。采用钢框架柱和工字形梁作为试验支撑装置，钢框架柱脚与地面导槽通过M28(10.9 s)地脚螺栓进行固定，工字形梁与钢框架柱顶面通过M12(8.8 s)高强螺栓进行连接。试验时将组合楼盖沿U形边梁方向的两个端部分别搁置在工字形梁翼缘上，采用连接件将U形边梁与工字形梁翼缘进行固定。U形边梁腹板与连接件通过ST5.5自攻螺钉进行连接，工字形梁翼缘与连接件进行焊接，以模拟两边支撑，梁端刚接的边界条件，见图4。

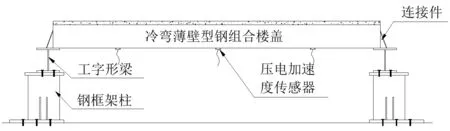
图4 试验装置Fig.4 Test device

为了测试冷弯薄壁型钢—石膏基自流平砂浆组合楼盖的基频，试验采用4种动荷载的加载方式：①体重为75 kg的男子以2 Hz步率分别沿着平行于C形楼盖梁方向、垂直于C形楼盖梁方向以及沿着组合楼盖对角线方向行走，见图5(a)～(c)，行走时间持续1 min。②体重为75 kg的男子采用激励锤沿着楼盖跨度及宽度方向用力竖向锤击组合楼盖面板，见图5(d)，每次锤击位置间隔300 mm，共锤击50次，每次采样持续试件为5 s，锤击位置,见图6。

(a)平行于C形梁方向行走 (b)垂直于C形梁方向行走

(c)沿着楼盖对角线方向行走 (d)激励锤敲击图5 试验加载方案Fig.5 Test loading program

1.4 试验测点布置

测试冷弯薄壁型钢-石膏基自流平砂浆组合楼盖在正常行走和激励锤激励下的动力特性时，采用压电加速度传感器测量楼盖的自振频率，测点布置见图7所示，图中D1～D20表示压电加速度传感器的编号，共20个，分别粘贴在C形楼盖梁的下翼缘位置处，另一端通过ICP转换头连接到LMS动态数据采集分析系统，采用时域法进行测定采集，采样频带宽为0～256 Hz。

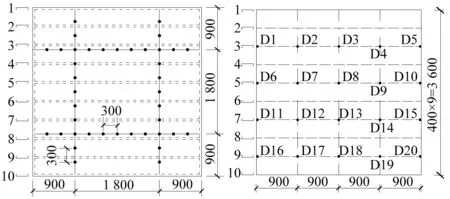
图6 激励锤锤击位置 Fig.6 Hammer position 图7 加速度传感器测点布置Fig.7 Layout of the measuring points

1.5 试验结果及分析

组合楼盖试件在4种荷载工况下的自振频率结果见表1，前3阶振型见图8和图9。试验结果表明:

(a)1阶振型 (b)2阶振型 (c)3阶振型图8 试件CF1振型图Fig.8 Vibration mode of specimen CF1

(a)1阶振型 (b)2阶振型 (c)3阶振型图9 试件CF2振型图Fig.9 Vibration mode of specimen CF2

(1)2个组合楼盖试件在正常行走和激励锤激励下的前3阶自振频率结果较为相近，表明楼盖的自振频率是结构本身固有的动力性能，并不会随着外部激励的改变而发生较大变化。

(2)试件CF2和试件CF1的前3阶自振频率较为接近，表明在石膏基自流平砂浆面板中增设钢丝网并不会显著增加楼盖的动力特性，楼盖的自振频率与抗弯刚度成正比，而设置钢丝网对组合楼盖的抗弯刚度影响较小。

(3)组合楼盖的振动形式以竖向振动为主，1阶振型表现为1个正弦半波沿楼盖梁方向的对称振动，2阶振型表现为2个正弦半波沿楼盖梁方向的反对称振动，3阶振型表现为3个正弦半波沿楼盖梁方向的反对称振动，符合楼盖的振动规律，表明采用压电加速度传感器获取的自振频率和振型结果较为准确。

(4)组合楼盖的动力响应与外部冲击荷载作用下的能量密切相关。图10为激励锤锤击作用下CF1试件沿C形楼盖梁长度方向和垂直于C形楼盖梁长度方向各测点的功率谱密度(PSD)分布图，曲线峰值点对应的频率即为楼盖的基频。由图可知：各测点测得组合楼盖的自振频率相近，表明组合楼盖的自振频率和频域分布与测点布置的位置无关，而各测点测得组合楼盖自振频率存在差异的原因为在动荷载作用下各楼盖梁的变形不能完全协调统一。

(a)沿梁方向PSD分布 (b)垂直于梁方向PSD分布图10 激励锤激励下CF1试件各测点的功率谱密度分布图Fig.10 Power spectral density distribution graph of CF1 specimen measuring points under hammer impact

(5)文献[9]建议冷弯薄壁型钢-OSB板组合楼盖的自振频率限值设为15 Hz，文献[10]提出采用10 Hz作为冷弯薄壁型钢-混凝土组合楼盖自振频率的控制指标，对比可知：在相同边界条件和构造设置情况下，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的自振频率介于上述两类组合楼盖的自振频率之间，原因为自振频率与质量成反比。综合国内外规范对楼盖自振频率限值的要求以及本文试验结果，建议冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的自振频率取不小于10 Hz作为控制指标，避免组合楼盖在外部激励作用下发生共振。

2 组合楼盖基频有限元模拟

采用ABAQUS有限元软件对冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频进行模拟分析，有限元模型示意图,见图11。

图11 组合楼盖有限元模型Fig.11 Finite element model of composite floor

在单元选取时，楼盖梁、边梁、压型钢板、支座加劲件、扁钢带以及刚性支撑件均采用壳单元S4R，石膏基自流平砂浆面板采用实体单元C3D8R，钢筋网采用桁架单元T3D2。模型中自攻螺钉连接均采用耦合螺钉连接位置处两个结点x,y,z三个方向平动自由度的方法进行模拟。在相互接触的构件间建立摩擦接触，法向作用采用硬接触，切向作用的抗滑移系数取为0.3[12]。采用tie约束来模拟石膏基自流平砂浆面板与压型钢板之间粘结性能，采用Embedded region命令将钢丝网嵌入石膏基自流平砂浆面板中。模型中冷弯薄壁型钢构件的本构关系采用双折线，按照材性试验结果进行选取，泊松比为0.3，钢材采用各向同性弹塑性材料模型及von Mises屈服准则。石膏基自流平砂浆采用各向同性弹性材料模型，弹性模量为2.34×104MPa，泊松比为0.2。在全局坐标系的Y方向定义重力加速度g=9.8 m/s2来考虑楼盖自重。约束U形边梁腹板x,y,z三个方向的全部自由度来模拟楼盖试件两边支撑、梁端刚接的边界条件，见图11。

对组合楼盖有限元模型进行振动模态分析，前3阶自振频率计算结果见表1，2个有限元模型的前3阶振型图相近，其中CF1模型的振型见图12。由图表可知，有限元模型能够较好地模拟组合楼盖在激励作用下的自振频率，有限元分析结果与试验结果误差小于12%，模型前3阶振型与试验测得前3阶振型相近，表明有限元模型正确，建模方法可靠。

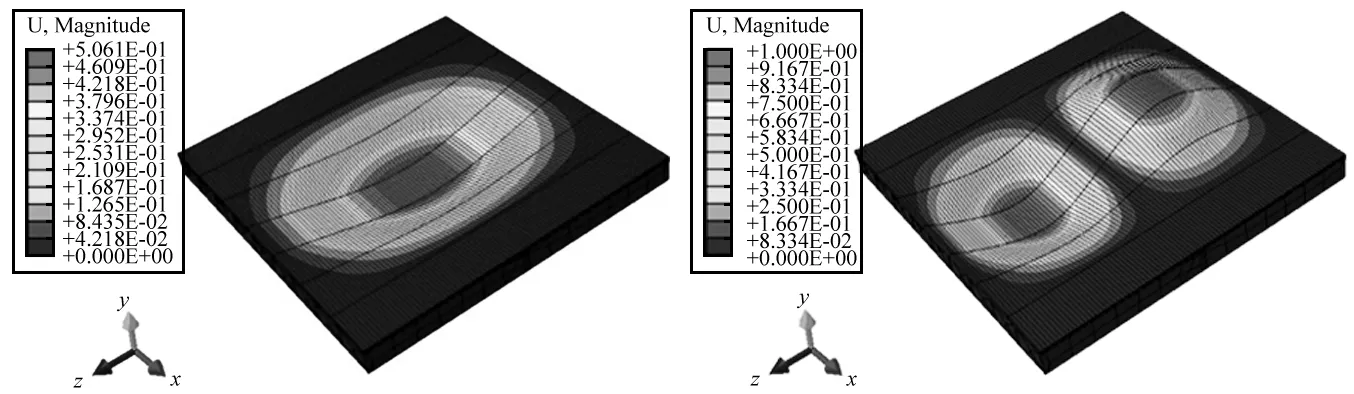
(a)1阶振型 (b)2阶振型

3 组合楼盖基频影响因素分析

基于验证后的有限元模型，研究楼盖梁板厚、楼面板厚度、楼盖跨度和宽度、构造措施等因素对冷弯薄壁型钢-石膏基自流平砂浆组合楼盖基频的影响。

除特别说明外，有限元模型尺寸为3.6 m×3.6 m，楼盖梁规格为C255×40×14×1.45 mm，间距为400 mm，边梁规格为U255×40×1.45 mm；压型钢板规格为YX-14-63-820 mm，厚度为0.75 mm；压型钢板与楼盖梁连接的自攻螺钉间距取周边间距为125 mm，中间间距为250 mm；石膏基自流平砂浆采用C30级，厚度为40 mm；楼盖跨中位置处扁钢带宽50 mm，厚1 mm，并在扁钢带中间及两端设置3个刚性支撑件，规格为C200×40×14×1.45 mm；楼盖模型的边界条件为两边支撑、梁端铰接以及两边支撑、梁端刚接。

3.1 楼盖梁板厚的影响

为研究楼盖梁板厚对组合楼盖基频的影响，建立楼盖梁规格为C255×40×14×tmm，板厚t分别为0.85 mm、1.15 mm、1.45 mm、1.75 mm、2.05 mm、2.35 mm和2.65 mm，共7个有限元模型，有限元基频结果见表4，组合楼盖的基频随楼盖梁板厚增大的变化曲线见图13。

由表4和图13可知，增大楼盖梁的板厚会提高组合楼盖的基频，而加强组合楼盖端部约束对基频的影响随着楼盖梁板厚的增大近似保持不变。当楼盖梁板厚由0.85 mm依次增大至2.65 mm时，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频依次增加约11.8%、3.1%、4.4%、0.2%、1.1%和2.4%，表明组合楼盖的基频与楼盖的抗弯刚度成正比。

表4 楼盖梁板厚的影响Tab.4 Influence of plate thickness of floor joists

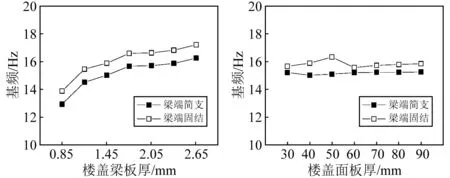
图13 楼盖梁板厚的影响Fig.13 Influence of plate图14 砂浆面板厚度的影响 Fig.14 Influence of mortar thickness of floor joistsslab thickness

《低层冷弯薄壁型钢房屋建筑技术规程》[13]JGJ 227—2011中规定冷弯薄壁型钢结构主要承重构件的壁厚不应小于0.75 mm，但对于多层住宅体系，建议冷弯薄壁型钢结构主要承重构件的壁厚不应小于0.85 mm，这与《冷弯薄壁型钢多层住宅技术规程》中规定相同。当组合楼盖采用厚度不小于0.85 mm的冷弯薄壁型钢承重构件时，楼盖的基频均大于10 Hz。

3.2 石膏基自流平砂浆面板厚度的影响

为研究石膏基自流平砂浆面板厚度对组合楼盖基频的影响，建立楼盖面板厚度分别为0 mm(无压型钢板)、30 mm、40 mm、50 mm、60 mm、70 mm、80 mm以及90 mm，共8个有限元模型，有限元分析结果见表5，组合楼盖的基频随楼盖面板厚度增大的变化曲线见图14。

由表5和图14可知：

(1)未设置组合板模型CF-0的基频比设置组合板模型CF-30的基频高出51.7%，原因为冷弯薄壁型钢梁骨架自重较轻，自振频率与质量成反比。模型CF-0因缺少压型钢板-石膏基自流平砂浆组合板对楼盖梁的组合效应，其面内外刚度远小于组合楼盖，致使模型CF-0前3阶振型和组合楼盖前3阶振型存在较大差别，如图15所示。模型CF-0的X向水平刚度较竖向刚度小，其振动形式以水平振动为主，而组合楼盖模型因存在组合板对楼盖刚度的贡献，楼盖的水平刚度大于竖向刚度，其振动形式以竖向振动为主。

(a)1阶振型 (b)2阶振型

(2)增大石膏基自流平砂浆面板厚度对组合楼盖的基频影响较小；除楼盖模型CF-50外，加强组合楼盖端部约束对基频的影响随着楼盖面板厚度的增加基本保持不变。当楼盖面板厚度由30 mm依次增大至90 mm时，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频依次增加约0.1%、1.7%、-2.0%、0.6%、0.2%和0.3%，原因为增大楼盖面板厚度一方面增加了组合楼盖的抗弯刚度，而另一方面也增大了组合楼盖的自重，可知组合楼盖的基频与楼盖的抗弯刚度成正比，而与楼盖的质量成反比。

为保证压型钢板与石膏基自流平砂浆能够协同工作，具备较好的黏结性能，要求在剪力分布最大区域内的石膏基自流平砂浆与压型钢板之间设置必要的抗剪件，同时考虑《建筑设计防火规范》[14]GB 50016—2014中对楼板防火保护层厚度的规定，建议组合楼盖的砂浆面板厚度不应小于40 mm，但砂浆面板过厚会增加楼盖的自重，故建议砂浆面板的厚度不应大于100 mm，同时压型钢板板肋宜垂直于楼盖梁布置，压型钢板板厚不宜小于0.75 mm。当组合楼盖采用厚度不小于40 mm的石膏基自流平砂浆面板时，楼盖的基频均大于10 Hz。

3.3 楼盖跨度的影响

为研究楼盖跨度对组合楼盖基频的影响，建立楼盖跨度分别为2 000 mm、2 800 mm、3 600 mm、4 400 mm、5 200 mm以及6 000 mm，共6个有限元模型，有限元分析结果见表6，组合楼盖的基频随楼盖跨度增大的变化曲线见图16。

由表6和图16可知，增大组合楼盖的跨度会显著降低楼盖的基频，加强组合楼盖端部约束对基频的影响随着楼盖跨度的增加近似保持不变。当楼盖跨度由2 000 mm依次增大至6 000 mm时，冷弯薄壁型钢—石膏基自流平砂浆组合楼盖的基频依次降低约45.0%、33.6%、26.1%、22.2%和20.0%，原因为增大楼盖跨度会增加楼盖的跨中挠度，降低楼盖的基频。

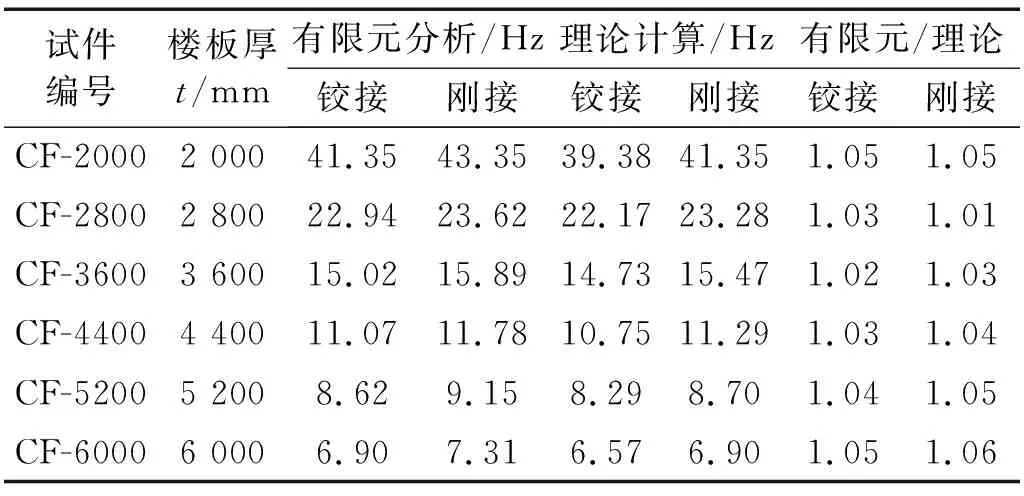
表6 楼盖跨度的影响Tab.6 Influence of floor span

以自振频率不小于10 Hz作为控制冷弯薄壁型钢—石膏基自流平砂浆组合楼盖振动的限值，建议组合楼盖的跨度不应大于4 400 mm，楼盖梁的挠度容许值，取l/300，以防止楼盖在使用过程中发生较大的振动，保证楼盖具有较高的基频。

3.4 楼盖宽度的影响

为研究楼盖宽度对组合楼盖基频的影响，建立楼盖宽度分别为2 400 mm、3 600 mm、4 800 mm、6 000 mm、7 200 mm以及8 400 mm，共6个有限元模型，有限元分析结果见表7，组合楼盖的基频随楼盖宽度增大的变化曲线见图17。

图16 楼盖跨度的影响Fig.16 Influence of floor span图17 楼盖宽度的影响 Fig.17 Influence of floor width

表7 楼盖宽度的影响Tab.7 Influence of floor width

由表7和图17可知，增大楼盖的宽度对组合楼盖的基频影响较小，加强组合楼盖端部约束对基频的影响随着楼盖宽度的增加近似保持不变。当楼盖宽度由2 400 mm依次增大至8 400 mm时，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频依次增加约1.8%、0.9%、0.6%、0.5%和0.6%。可知对于沿U形边梁支撑的组合楼盖，其基频基本不受楼盖宽度变化的影响，从而可满足建筑使用上大空间的功能要求。

当组合楼盖跨度满足要求时，改变楼盖的宽度对楼盖的基频影响较小，楼盖的基频均大于10 Hz。从而为组合楼盖整体模型简化为T形截面组合梁模型来计算组合楼盖的基频提供了依据。

3.5 楼盖构造措施的影响

为研究扁钢带和刚性支撑件布置间距对组合楼盖基频的影响，有限元模型中扁钢带分别采用在楼盖梁跨中布置1道和在楼盖梁1/3跨各布置1道两种方式，刚性支撑件分别采用不设置、沿扁钢带方向间隔1.6 m 设置1个以及沿扁钢带方向间隔0.8 m设置1个三种方式，共6个有限元模型，有限元分析结果见表8，组合楼盖的基频随楼盖构造措施加强的变化曲线见图18。

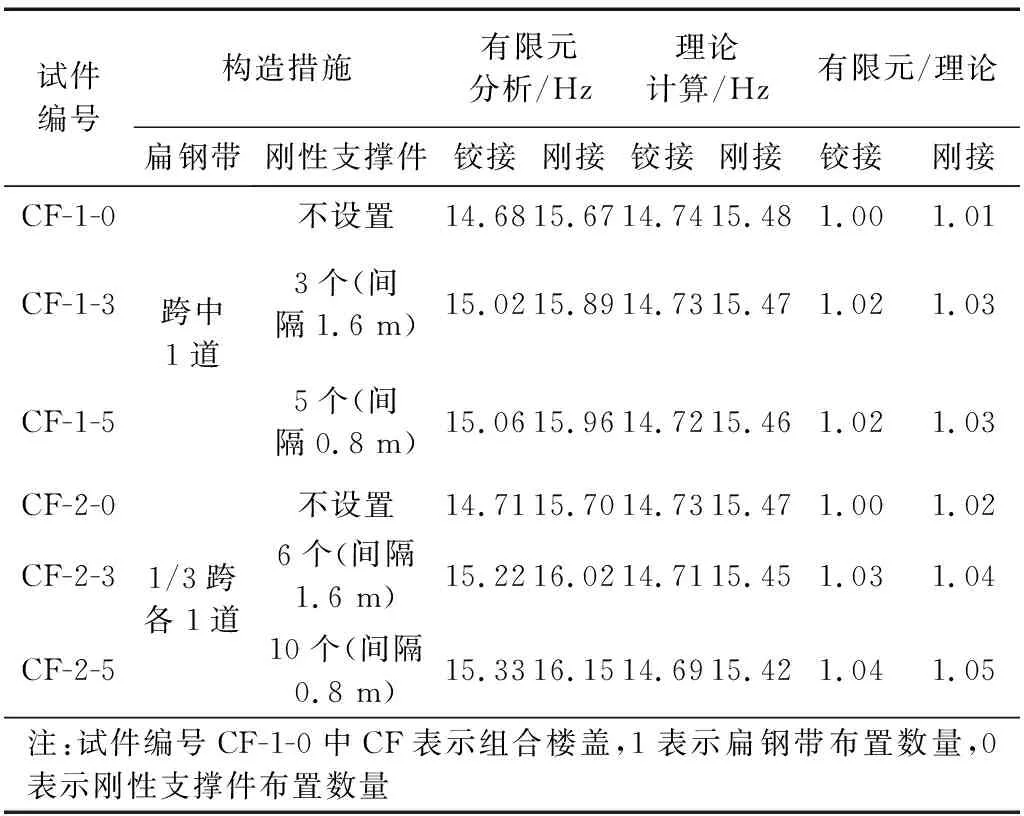
表8 楼盖构造措施的影响Tab.8 Influence of construction measurement

(a)扁钢带跨中布置 (b)扁钢带三分点布置图18 楼盖构造措施的影响Fig.18 Influence of construction measurement

由表8和图18可知，加强组合楼盖的构造措施对楼盖的基频影响较小，加强组合楼盖端部约束对基频的影响随着楼盖构造措施的加强近似保持不变。当楼盖设置1道扁钢带，刚性支撑件的数量由0增加至5时，组合楼盖的基频依次增加约1.9%和0.4%；当楼盖设置2道扁钢带，刚性支撑件的数量由0增加至10时，组合楼盖的基频依次增加约2.8%和0.8%；模型CF-2相比于模型CF-1，随着刚性支撑件数量的增加，组合楼盖的基频依次增加约0.2%、1.1%和1.5%。由此可知，仅在组合楼盖跨中位置设置扁钢带，并在扁钢带两端和中间设置刚性支撑件就能获得较好的振动性能，同时加强了楼盖梁的侧向稳定性，故建议当楼盖跨度超过3.6 m时，在楼盖梁下翼缘跨中处应设置通长钢带支撑和刚性支撑件，其中钢带宽度不应小于50 mm，厚度不应小于1.0 mm；刚性支撑件截面形式应与楼盖梁相同，厚度不应小于1.0 mm，并沿钢带方向均匀布置，且应在钢带两端设置，这与《低层冷弯薄壁型钢房屋建筑技术规程》[13]JGJ 227—2011中规定相同。

在组合楼盖跨度满足要求的前提下，采取扁钢带和刚性支撑件等构造措施，可保证组合楼盖的基频大于10 Hz。

4 组合楼盖基频理论计算

4.1 T形组合梁的换算截面惯性矩

由楼盖宽度影响因素分析结果可知，对于沿U形边梁支撑的组合楼盖，其基频基本不受楼盖宽度变化的影响。在冷弯薄壁型钢结构体系中，组合墙体对楼盖的端部约束并不能达到刚接的边界条件，可将楼盖的端部边界条件简化为铰接约束。综上，可将冷弯薄壁型钢组合楼盖等效为具有均匀质量和刚度的简支T形截面组合梁模型来计算其自振频率，见图19。

(a)形心轴位于C形梁上 (b)形心轴位于砂浆面板内图19 T形截面组合梁模型Fig.9 T-shaped model of composite joist

组合梁在正弯矩作用下按弹性理论进行截面分析时，根据截面应变相同且总内力不变的原则，将受压石膏基自流平砂浆面板的有效宽度be折算成与钢材等效的换算宽度beq，构成单一材质的换算截面。组合梁砂浆面板的计算厚度应取压型钢板波峰以上石膏基自流平砂浆的厚度hc1。计算T形组合梁的换算截面惯性矩时，应按组合梁形心轴的位置，分两种情况分别考虑：

(1)形心轴0-0位于C形梁上，见图19(a)

(1)

(2)形心轴0-0位于砂浆面板内，见图19(b)

(2)

式中：be为石膏基自流平砂浆面板的有效宽度；b0为C形梁的翼缘宽度；b1和b2分别为C形梁外侧和内侧的面板计算宽度；h为组合梁截面的高度；hc2为压型钢板的波高；αE为钢材弹性模量与石膏基自流平砂浆弹性模量的比值；A0为组合截面的面积；As为C形梁的截面面积；Ac为石膏基自流平砂浆面板的截面面积；Is为C形梁的截面惯性矩；Ic为石膏基自流平砂浆面板的截面惯性矩；I0为T形组合梁的换算截面惯性矩；y为C形梁形心位置至组合截面顶面的距离；x为组合截面形心轴至组合截面顶面的距离。