基于新型材料的吸振器设计及电流控制方法*

宋伟志， 姚永玉， 赵海军,2， 赵红霞， 岳遂录， 陈智勇

(1.洛阳理工学院机械工程学院 洛阳，471023) (2.天津职业技术师范大学汽车与交通学院 天津，300222)

引 言

吸振器发明于1902年，因为性能稳定，设计简单而应用广泛[1]。被动式吸振器对于单频激励减振效果明显，但不适应宽频减振[2]。近些年自适应吸振器[3-7]得到了快速发展。其结构参数(刚度、阻尼、质量等)可调，故兼具结构简单、有效减振频带宽、无需大量能源供应等优点。但现有自适应吸振器多少存在一些缺点。如文献[3]所提吸振器，通过调节液体质量改变吸振器固有频率，实现宽频减振，但响应速度慢，同时在改变液体质量过程中可能引起振动能量发散。文献[6]所提吸振器响应速度快，但添加吸振器引起受控系统新的共振峰。文献[7]利用形状记忆合金可以拓宽减振频带，但响应速度慢。磁流变弹性体(magnetorheological elastomers，简称MRE)不易产生沉降[8]、剪切模量可控且响应速度极快，是理想的吸振器刚度元件。文中以MRE作为刚度元件设计吸振器，减振频带可拓宽，且响应速度快；对变质量减振系统涉及质量控制策略[9-11]进行改进，提出适用于刚度调节的电流控制方法，以消除增加吸振器而引起的受控系统新的共振峰；同时文中还分析了MRE的材料组成及磁流变(magnetorheological,简称MR)效应的机理。

1 MRE磁流变效应及系统仿真分析

在原材料不同配比下，分别给励磁线圈供以0～1 A的电流，对制备的MRE进行移频实验，见图1。结果表明当成分组成为羟基铁粉60%、硅橡胶20%、硅油20%时，MRE的移频特性最为明显，即采用上述质量比例时，制备的MRE磁流变效应最好。

图1 移频实验系统Fig.1 Frequency shift experiment system

MRE的MR效应机理为磁偶极子理论[12]。MRE在预屈服阶段工作[13]，其力学性能常采用剪切模量G，具体包括储能模量及损耗模量，其值受工作频率及环境温度影响[14]，可表示为

(1)

其中：Gc为储能模量；Gs为损耗模量；η为损耗因子；j为虚数单位。

实验研究证明η在不同磁场下没有明显变化[14]，磁流变效应主要表现为Gc的变化，故可将式(1)写成

G=G0+ΔG

(2)

其中：G0为初始模量；ΔG为加入磁场后模量的增量。

考虑励磁性颗粒的空间结构，当剪切受力方向与链状结构垂直时，励磁性颗粒磁总能可表示为

(3)

其中：m为磁场下产生的磁偶极矩；μ0为绝对导磁率；μf为基体相对导磁率；x，y，z为某一研究励磁性颗粒的空间坐标；γ为应变。

设x=kD0，y=mD0，z=nd0(k,m,n取整数)。求解中心颗粒的所有作用能同时对γ求导，易得ΔG

(4)

其中：R为励磁性颗粒球半径；λ=D0/d0,D0为链间距，d0为颗粒间距，理想情况下励磁颗粒间距相等;φ为体积比浓度。

考虑励磁颗粒场间相互效应，近似求得单链模型ΔG的简化结果

(5)

当d0≫R时，式(5)可写为

(6)

即为磁偶极子模型。

通过上述分析，在MRE未达到磁饱和前，其模量随外加磁场的增加而增加。

以MRE为弹性元件设计吸振器，见图2，吸振器刚度[14]为

(7)

其中：A为MRE端面面积；h为MRE厚度。

图2 基于MRE自适应吸振器Fig.2 ADVA based on MRE

由实验系统结构建立运动方程[11]为

(8)

其中：m1,c1,k1分别为受控系统质量、阻尼及刚度；m2,c2,k2分别为吸振器质量、阻尼及刚度。

求解上述方程易知当吸振器固有频率ω0为

(9)

与外界激频ω相等时，减振效果最好[2]，理想情况下可使受控系统振幅为零。根据式(8)建立系统仿真模型，仿真中参数选择如表1，各参数采取国际标准单位制。

表1 系统结构参数

仿真中对受控系统有无吸振器进行了幅频分析，结果见图3。 图中，P点为引入吸振器后，受控系统新增的共振点，V点为吸振器有效工作点。

图3 受控系统幅频特性Fig.3 Controlled system amplitude-frequency

根据上述分析可知，当ω0=ω时，受控系统幅频值为-39 dB(V点)，吸振效果显著，然而有效减振区域仅为一点。同时与无吸振器时的受控系统比较易发现，受控系统新增一个共振峰(P点)。调节吸振器刚度以改变其固频，可实现拓宽频带的目的，具体实施结果见图4，图5。

由图4，图5可知，在刚度由18 N/m连续变化至27 N/m时，吸振器工作频带被有效拓宽。

图4 吸振器拓频效果Fig.4 absorber widen frequency effect

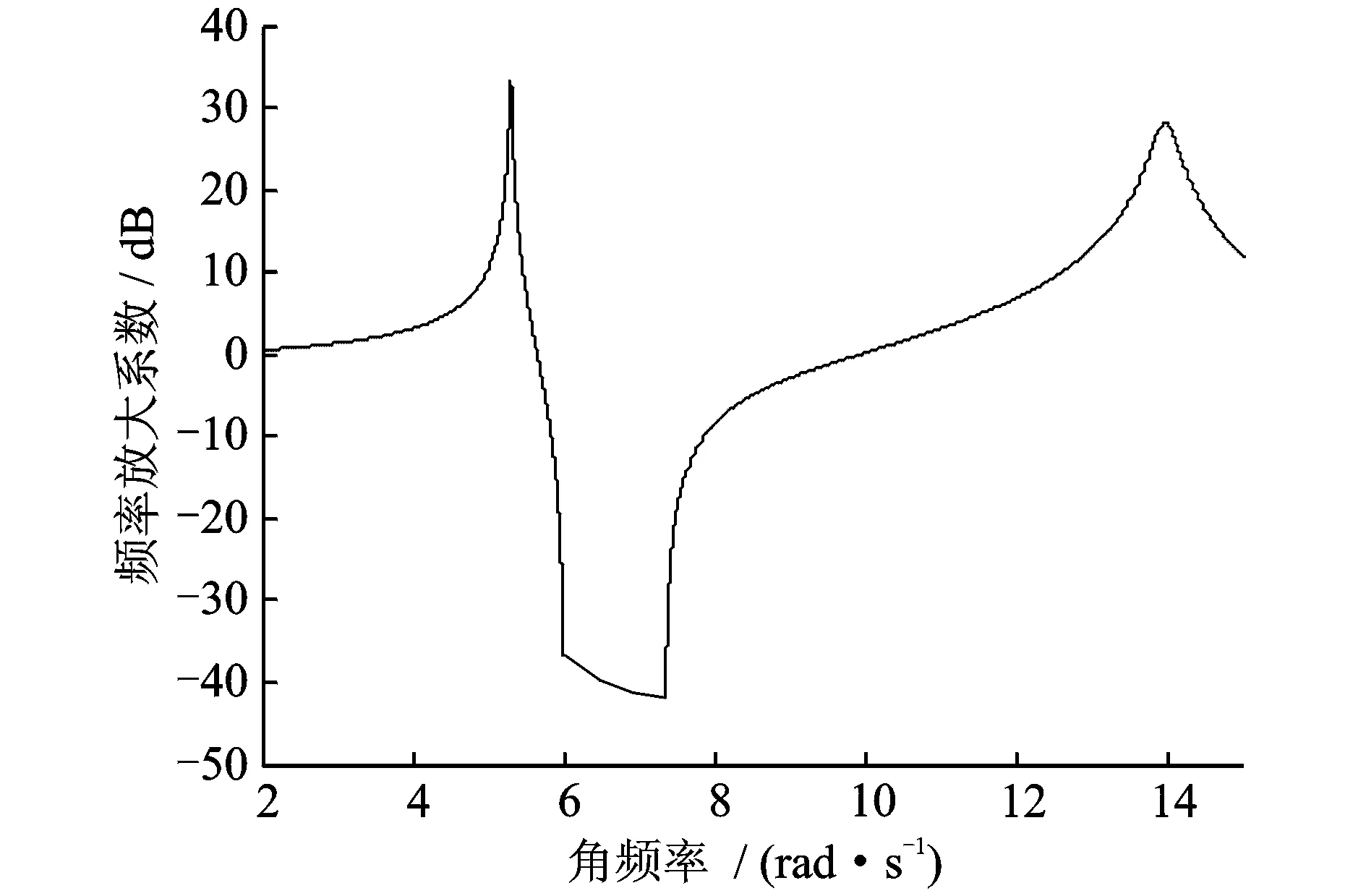
图5 形成有效频带Fig.5 Form an effective band

基于Simulink仿真，对受控系统进行时域分析。根据ω调节k2，使得ω0=ω，以保证吸振器高效的工作性能。图中在第100 s和300 s调节刚度，实现对外界激振频率的追踪(即ω0=ω)。图中外界激振频率ω在第200 s时发生改变。

图6 时域响应Fig.6 Time domain response

由图6吸振器减振效果可知，通过调节吸振器刚度，使得吸振器固有频率等于外界激振频率，可显著提高吸振器的工作性能，同时拓宽了吸振器减振频带。

2 基于MRE的动力吸振器实验分析

建立图7所示实验台，实验中采用正弦扫频，激振信号由激振器3产生，加速度传感器4采集受控系统振动信号，经电荷放大器8给数据采集仪2，再经数据处理单元1进行处理分析。过程中，通过可控电源7调节励磁电流实现MRE外加磁场的控制，电流调节范围为0～1.50 A。分析受控系统在不同电流作用下的幅频特性曲线，结果如图8所示。

图7 MRE的自适应吸振器实验台Fig.7 Adaptive vibration absorber test bench based on MRE

图8 吸振器拓频效果Fig.8 absorber widen frequency effect

由图8可知，当电流从0增加到1.50 A的过程中，曲线波谷(吸振器固频)由20.89 Hz平移到了32.26 Hz，频带达到11.37 Hz。

根据图8拟合频率f及电流I间的关系，如表2所示。

表2固有频率与电流关系

Tab.2Relationshipbetweennaturalfrequencyandcurrent

电流/A0.000.501.001.50固有频率/Hz20.8925.6330.0832.26

根据表2，对实验中吸振器电流进行控制，与被动吸振器减振性能进行对比，对比结果如图9所示。

图9 被动及自适应吸振器减振性能对比Fig.9 Vibration performance comparison of PDVA and ADVA

通过图9对比表明，自适应吸振器可以明显拓宽减振频带。同时发现，受控系统新增的共振峰仍然存在，如P点所示。

根据表2与图8，采集受控系统所受激振频率，提出实验中电流的控制方法，以消除新增的共振峰。电流控制具体流程如图10所示。

图10 电流控制流程Fig.10 Current control flow

对吸振器施加电流控制方法后，受控系统幅频特性曲线如图11所示。

图11 电流作用下受控系统幅频特性Fig.11 Amplitude-frequency of the controlled system under current action

由图11可知，利用上述提出的电流控制方法可以消除由于增加吸振器而引起受控系统新的共振峰。同时，实验对受控系统的时域进行了分析，具体结果如图12所示。

开始阶段通过幅频分析得到激振频率24.9 Hz，电流采用0.5 A，随着激振频率变为19.19 Hz，系统振动加剧，由上述电流方法调节电流为0 A，调节后结果见图12。

图12 消除共振效果Fig.12 eliminates resonance effects

图12同样表明，利用上述提出的电流控制方法调节电流，可有效消除由于添加吸振器而引起的受控系统新的共振峰，其振动幅值由原来的1.96 mm降低至1.23 mm，降幅达37.2%。

3 结束语

由磁偶极子理论可知,在磁饱和前MRE剪切模量与穿过磁场平方成正比；实验中受控系统幅频特性说明设计的吸振器有效拓宽了减振频带，约为11.37 Hz；通过频域及时域分析说明了提出的电流控制方法可有效消除共振峰，使受控系统振幅降低达37.2%，此方法易于实施且适用于其他自适应吸振器，具有较好的工程应用价值。