论证视角下的“三角形内角和”教材理解与教学设计（四）——如何基于论证过程开展教学

◇宋煜阳

（上接第4期第66页）

一、解读课题，认识内角，梳理研究思路

1.理解题意，指认内角。

揭题板书：三角形内角和。

师：你明白课题的意思吗？说说什么是三角形的内角。

出示锐角三角形、直角三角形、钝角三角形（如图 1），介绍：“像图中∠1、∠2、∠3 都是三角形相邻的两条边的夹角，称为三角形的内角。”“我们常说的三角形有3个角指的就是三角形的内角。”

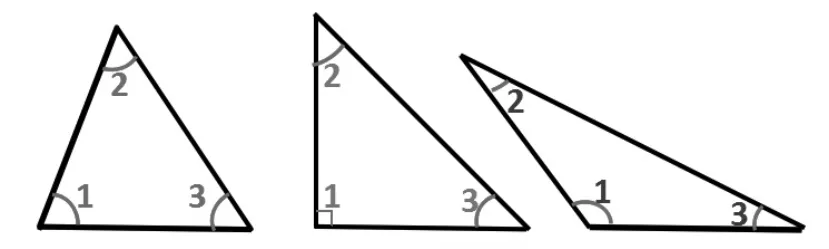
图1

出示△ABC，在边BC上取一点D，连接AD得到△ABD、△ACD （如图2），组织学生指认△ABD、△ACD、△ABC的内角。

图2

讨论：∠3、∠6是△ABC的内角吗？你是怎么想的？

2.摸底了解，明确研究对象。

交流讨论：关于三角形内角和，你已经知道了哪些知识？哪些三角形的内角和是180°？

结合学生回答，教师板书：所有三角形的内角和都是180°。

师：所有三角形你们都研究过吗？看来，还得在“所有三角形的内角和都是180°”后面打上问号。

板书：所有三角形的内角和都是180°？

组织学生讨论：该怎么研究这个结论？

结合学生想法指出：要研究三角形内角和是不是180°，就需要研究所有三角形内角和是不是180°，也就是要研究所有直角三角形、所有锐角三角形、所有钝角三角形内角和是不是180°。

二、运用不完全归纳法论证“直角三角形内角和是 180°”

1.研究特殊直角三角形的内角和。

出示一副三角尺，组织学生讨论：这两个直角三角形的内角和是180°吗？你是怎么知道的？

针对两个特殊直角三角形的已知内角度数，口算得出“90°+30°+60°=180°”“90°+45°+45°=180°”，结论正确。

讨论：凭这两个直角三角形内角和是180°这个结论，可以说明所有直角三角形的内角和都是180°吗？

学生通过讨论得出，直角三角形有许多个，不能凭这两个直角三角形内角和是180°而得出“所有直角三角形内角和都是180°”的结论。还需要验证其他直角三角形内角和是不是180°。

2.研究其他直角三角形内角和。

教师提供多组直角三角形（90°，15°，75°；90°，20°，70°；90°，40°，50°；90°，35°，55°）供学生研究。

组织学生反馈：你研究的直角三角形内角和是180°吗？你是怎样得出这个结论的？

对学生的测量结果进行汇总，并补充几何画板数据，观察讨论：有没有哪个直角三角形的内角和不是180°的？

得出结论：所有直角三角形的内角和都是180°。

结合学生作品，引导学生发现用撕拼法也可以验证直角三角形内角和是180°。

3.梳理小结研究方法与结论。

通过以上探究，教师指出，刚才我们通过测量求和、撕拼等方法发现，所有直角三角形内角和确实是180°。

三、运用推理分析方法论证锐（钝）角三角形内角和是180°

梳理锐角三角形、钝角三角形内角和的研究思路。

讨论：你用哪些方法来研究说明锐角三角形、钝角三角形的内角和也是180°？

师：除了测量求和、撕拼等方法来研究说明锐角三角形、钝角三角形内角和，你还有其他研究方法吗？你能利用直角三角形内角和是180°这个结论来说明吗？

通过小组讨论，得出将锐角三角形作高，分割为两个直角三角形进行推算（如图3）。反馈讨论：“180°×2-90°-90°”是什么意思？为什么要减去两个90°？结合图示辨析，明确∠4、∠5并非△ABC的内角，所以减去两个90°。

图3

让学生独立思考：如何利用直角三角形内角和结论来说明钝角三角形内角和是180°？

学生通过画图、推理分析并交流，重点辨析“为什么减去 180°”。

回顾反思：刚才我们是怎样研究说明锐角三角形、钝角三角形内角和是180°的？需不需要研究其他锐角三角形、钝角三角形内角和？

通过讨论得出，锐（钝）角三角形内角和可以通过作高转化为直角三角形进行研究，因为每个锐（钝）角三角形通过作高都可以得到直角三角形，所以不需要研究很多个。

四、梳理研究过程与方法，确认研究结论

引导学生研究发现，通过测量求和、撕拼、推理分析等研究方法得出所有直角三角形、锐角三角形、钝角三角形的内角和都是180°，因此可以得出结论：所有三角形的内角和都是180°。

五、全课总结，鼓励质疑

师：这节课你有哪些收获？还有什么问题？

结合学生提出的 “为什么三角形内角和是180°”“有没有三角形的内角和不是 180°”的问题，鼓励学生通过查阅资料寻求答案。