《勾股定理》说课设计
2018-11-01安徽省阜阳市第十五中学陈景涛
安徽省阜阳市第十五中学 陈景涛
一、教材分析
1.教材的地位与作用
《勾股定理》是人教版八年级数学下册第18章的起始课,它是在学生已经掌握了直角三角形的有关性质的基础上进行学习的,它揭示了直角三角形三边之间的数量关系。
本节对后续学习九(下)解直角三角形有着重要的思维润滑作用。勾股定理被喻为数形结合的第一定理,在数学的发展中有着非常重要的作用(如它导致了无理数被发现)。本节是对直角三角形的进一步认识和理解,它在整个第三学段乃至整个知识体系中起着非常重要的作用。
2.教学目标
知识技能:能说出勾股定理的内容,并能用勾股定理解决简单实际问题。
数学思考:在勾股定理的探索过程中,发展学生合情推理能力,体会数形结合的思想。
解决问题:①通过拼图活动,体验数学思维的严谨性,发展形象思维。②在活动中,学会与人合作并能与他人交流思维的过程和探索的结果。
情感态度:①通过对勾股定理历史的了解,感受数学文化,激发学习热情。②培养学生倾听、感悟的欣赏意识,体验解决问题方法的多样性,培养探索的自信及数学的应用意识。
3教学重难点
重点:勾股定理的证明和初步应用。
难点:利用数形结合的方法验证勾股定理。
二、学情分析
一方面,之前学生学习直角三角形的有关性质及正方形面积算法,已有了相当丰富的生活经验和知识储备,具备了一定的独立思考能力和探究能力,而且他们思维活跃,乐于展示,勇于创新。这将是我成功探究新课的优势。另一方面,八年级学生还是以感性认识为主,并向理性认识过渡,所以我对本节课设计了观察、实验、操作(画、量、算)等多种数学活动,引导学生采用自主探索和合作交流相结合的学习方式。此外,学生缺乏严谨的逻辑推理能力及知识的综合应用能力,教学中要引起足够重视。
三、教法、学法
1.教学方法
教育家皮亚杰说过教师的工作不是教给学生什么,而是着力构建知识结构,并用种种方法刺激学生的求知欲。结合学情,我主要采用了引导探究式教学方法,先由浅入深,由特殊到一般地提出问题,接着引导学生通过实验操作,验证,在学生的自主探究、合作交流中解决问题,这样既遵循了学生的认识规律,又充分体现了“学生是学习的主人,教师是数学学习的组织者、引领者和合作者”的教学理念。
2.学法指导
“操作+思考”的方式符合八年级学生的认知水平,适应其思维发展规律及心理特征,本节充分发挥教师学生的“双主”作用,通过教师引导学生动手动脑,主动探索获得新知,进一步理解运用归纳猜想,由特殊到一般,数形结合等数学思想方法解决问题。同时让学生感悟到学习任何知识的最好方法是自己去探究。
四、教学过程
(一)教学热身运动
1.三角形三边关系:两边之和第三边,两边之差第三边。直角三角形三边满足这个关系吗?
2.你知道哪些有关直角三角形的知识?
3.你能给同伴提出一个有关直角三角形的问题,并让其作答吗?
“兴趣是最好的老师”,可见兴趣是影响教学效果的重要因素。如何在课的一开始就深深地吸引学生呢?我的体会是:让学生“在玩中做,在做中玩”。这里的“抽签”不仅拉近了师生之间情感交流距离,也为探究新知铺平了道路。特别是第三个开放性问题,这是我有意架设的“桥梁”,我会根据情形,将学生的关注点引入新课。
(二)问题情境导入
这一环节我是这样的预设的:利用多媒体资源制作了声音、图像,动画三位一体的幻灯片。(今天,人类为了寻求与“外星人”接触的可能性,已向太空发射了一批物件,其中包括地球人男女形象,各种物质和元素符号,而数学家华罗庚提出了一种新颖的独特设想:用数形关系向宇宙发出邀请……)顺势问学生:你见过这个图案吗?你听说过勾股定理吗?让我们沿着一位哲学家的足迹来探索。
教师是教学情景的设计者,好的情景往往可收到事半功倍的效果。这样设计,学生的胃口显然已被调起来了,接下来便可进行新课探究。
(三)享受探究乐趣
此环节是教学过程的重心,目标的落实、重难点突破、课堂的和谐度都将在此展现。为此,我设计了一些探究活动,让学生经历“探究—猜想—归纳—验证”的数学发现过程。
1.观察:等腰直角三角形三边关系
这里通过把毕达哥拉斯的地砖问题抽象为数学问题,让学生感受到生活处处有数学,同时引导学生将生活图形数学化。利用图形,学生通过直接数等腰直角三角形的个数或者用割补的方法将正方形A、B中小等腰直角三角形补成一个大正方形。学生易发现正方形A、B、C的面积之间的数量关系:。然后启发学生用三角形的边表示面积,进而发现:等腰直角三角形的三边满足“两直角边的平方和等于斜边的平方”。从低起点的问题入手,这样做有利于学生参与探索,感受数学学习过程,有利于激发学生学习学习兴趣,体验成功的快感。
2.探究:一般的直角三角形三边关系
等腰直角三角形有上述关系,一般的呢?(这样设疑突破了等腰直角三角形的狭小圈子,让问题趋于一般化,增强学生对以上关系的认同感,为后面的勾股定理的现身提供了探索导向)
我把学生分成两大组,让学生利用网格纸计算以直角边为2、3和3、4的直角三角形向形外作的三个正方形的面积。
此时以斜边为边的正方形面积求法是本节课的难点所在,难点处正是学生互相学习,充分交流思维的好时机。(探索中学生可能出现以下困难:①确定斜面边上正方形的另外两个顶点;②以斜边为边长的正方形面积计算。针对①,建议学生用圆规、直尺作图寻求;对于②,则引导学生类比等腰直角三角形的探究方法去解决。)
在此要给学生充分自主探索的时间与空间,学生思维的闪光点也正是在这种讨论的过程中被发现的。对于学生的计算方法,教师在参与学生活动中适时鼓励、肯定、纠正。学生充分交流后,两组同学推荐代表汇报计算结果。预设:学生将展示割(图1)、补(图2)、
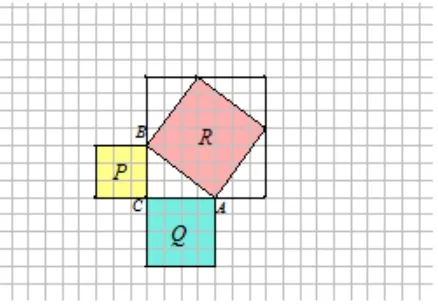
图2
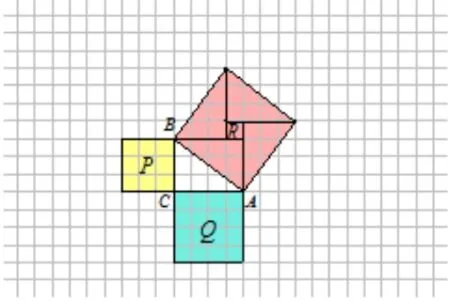
图1
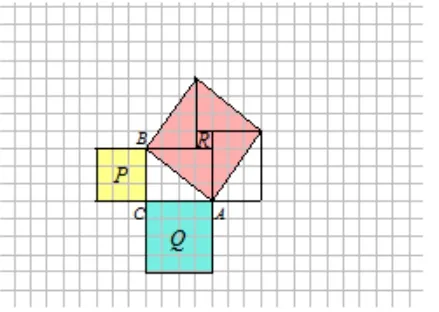
图3
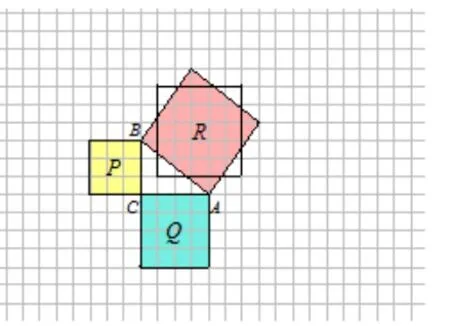
图4
平移(图3)、旋转(图4)四种方法。旋转这种方法只适用于斜边为整数的情况,况且学生还不会计算斜边长,没有一般性,若有学生提出,应给学生以解释。
肯定学生的研究成果,进而引导学生总结:把图形进行“割”和“补”,即把不能利用网格线直接计算面积的图形转化成可以利用网格线直接计算面积的图形,让学生体会化归的思想。
3.猜想:命题1
经历以上数学活动,我们利用面积关系揭示出直角三角形三边之间关系,这个关系用命题形式怎样表述?
命题1:如果直角三角形两直角边长分别为a、b,斜边长为c,那么。(这一问题的结论是点睛之笔,应充分让学生交流、表达)
4.利用拼图验证猜想
猜想是逼近结论的关键一步。是否所有的直角三角形都有这样的特点呢?我们如何验证任意三角形三边也满足这个关系呢?
在探索定理的过程中,按从网格到脱离网络的序列进行,对学生而言是思维的完善和飞跃,利用弦图证明勾股定理,不但拓展了学生的视野,激发了学生的探究热情,而且使学生感受到勾股定理证明的博大精深。
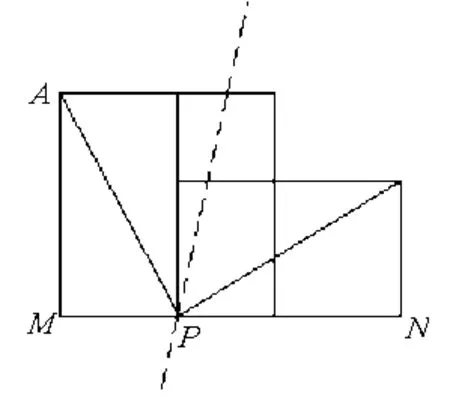
组织学生利用手中的学具(边长分别为a、b的两个连体正方形纸片),进行拼图活动。这里需要说明的是:我们引导学生拼图的关键是“构造以a、b为直角边的直角三角形”。若有学生盲目动手,如沿正方形对角线分割等,要及时引导学生自我反思、校正,在不断摸索中找到解决问题的办法。对于“剪切点”的确定是学生操作的难点,根据情况可建议学生:通过折叠,让大正方形的左上角顶点(A)和连体图形中的小正方形的右下角顶点(N)重合,折痕与MN的交点,即为“剪切点”(如右图所示)。剪拼操作后,学生容易想到:未剪之前,图形面积是a2+ b2,在拼图过程中,构造了以a、b为直角边的直角三角形,得到斜边为c。拼接之后新的正方形边长是c ,面积为c2。从而得到直角三角形三边的关系:a2+b2=c2。
通过拼图活动,调动学生思维的积极性,建立初步的空间观念,发展形象思维。让学生模拟数学家思维方式和思维过程,再通过动手操作和演示确信结论的正确性,然后利用“弦图”借助面积关系、代数公式给出证明,体会数形结合思想,发展创造性思维能力。
5.得出结论:勾股定理
这一环节是本节从感性到理性的具体体现。它是前面数学活动的深化和提升。对于定理的概念教学和“勾股”的释义,我采取适时点拨的做法:
(1)定理:经过证明被确定为正确的命题称为定理。
(2)引导学生对定理用“文字”和“符号”两种语言表示,并熟悉定理数学表达式的变形。
6.“勾股世界”和“身边的勾股”
结合我校学生实际,我预设了“勾股世界”和“身边的勾股”。
(1)播放音频资料“勾股世界”。
(2)引导学生举例“身边的勾股”(如课本封面、十五中标志图、章前图等)。
(这样设计意在激发学生学习热情和爱国主义情感,同时感受到数学就在身边,体现“数学生活化”思想)
至此,在学生动手操作,自主探究、合作交流的活动中,验证了勾股定理,本节重难点自然就得以突破了。
(四)乘坐智慧快车
学以致用,下面我邀请大家“乘坐智慧快车”尝试解决问题。这一环节,我设计的问题是呈阶梯状的练习:先是较基础的理解性练习,再是拓广型的应用性练习。俗话说:“授之以鱼,不如授之以渔。”两类练习之间我设计了一个“温馨提示”,既是对理解性练习的小结以及应用勾股定理注意事项的提醒,也为“拓广应用”作出了思路点拨,可谓承上启下,一箭双雕。
学生的个人知识、直接经验、生活世界都是重要的课程资源。因此,我这里选取的多是贴近学生生活的实例,让学生在解决问题中体会成功的喜悦,进一步体会勾股定理的广泛应用,增强了用数学的意识。
(五)分享你我收获
通过学习你有什么收获呢?
1.这节课你学习了哪些知识?
2.你还有什么疑惑?
(学生一般临近下课,大脑处于疲劳状态,注意力开始有所分散,此举可将学生兴奋心理再度点燃)
通过谈收获:①可培养学生归纳和语言表达能力。②让学生谈收获教师回收到的不仅有知识技能达成情况,还有过程体验、数学思考,解决问题、情感态度的形成情况。
(六)开拓数学天地
作业第一题面向全体学生要求,第二题根据弹性时间的盈余决定安排在课内或课外。
新课程强调发展学生数学交流的能力,用课堂纪实给学生提供了一种表达思想和情感的方式,以体现评价体系的多元化、人文化。
课外探索的设计有利于激发学生的探索欲、求知欲。同时让数学课堂因探究而继续延伸和精彩下去。
五、教学设计反思
我结合实际,从学生喜闻乐见的“外星问题”导入,以学生熟悉的事物(如校园内的草坪、十五中标志图、课本封面)为“佐料”,整合利用教学资源,有序组织数学活动,力求本节数学课成为动态的知识生成过程,成为学生主动探索求知的过程。自始至终,做到关注学生个性发展,贯彻“以人为本”的科学教育观。回顾整节课,我从“活动”和“评价”两个方面再作如下说明。
关于活动安排:通过“问题情境”和“媒体演示”激发学生的兴趣,吸引学生参与活动;通过探究活动、说说心里话,鼓励学生主动参与活动,通过“乘坐智慧快车”促进学生参与活动。
关于评价:在教学活动中,注重对学生进行即兴评价;在“课堂纪实”中,安排多维评价,用以发展学生数学交流的能力。用“课堂纪实”给学生提供了一种表达思想和情感的方式,以体现评价体系的多元化、人文化。
