具有垂直传染和脉冲接种的甲肝传染病模型

李录苹，孔丽丽

（山西大同大学数学与统计学院，山西大同037009）

传染病大量存在于现实生活中,人们运用数学工具对疾病的传播控制进行研究是数学中的一个重要研究方向[1-3]。甲型肝炎病毒主要通过粪-口途径传播,传染源多为病人。甲型肝炎的潜伏期为15～45天,病毒常在患者转氨酸升高前的5～6天就存在于患者的血液和粪便中。发病2～3周后,随着血清中特异性抗体的产生,血液和粪便的传染性也逐渐消失。而且甲肝病毒能通过破裂的胎盘由母亲血循环进入胎儿血循环,导致新生儿获病[4]。甲肝患者病愈后,可获得终身免疫力[5]。因此,在甲肝传染病研究过程中考虑垂直传染和预防接种问题是非常有必要的。

1 模型的建立

考虑具有垂直传染和脉冲接种的甲肝传染病模型,建立的模型如下:

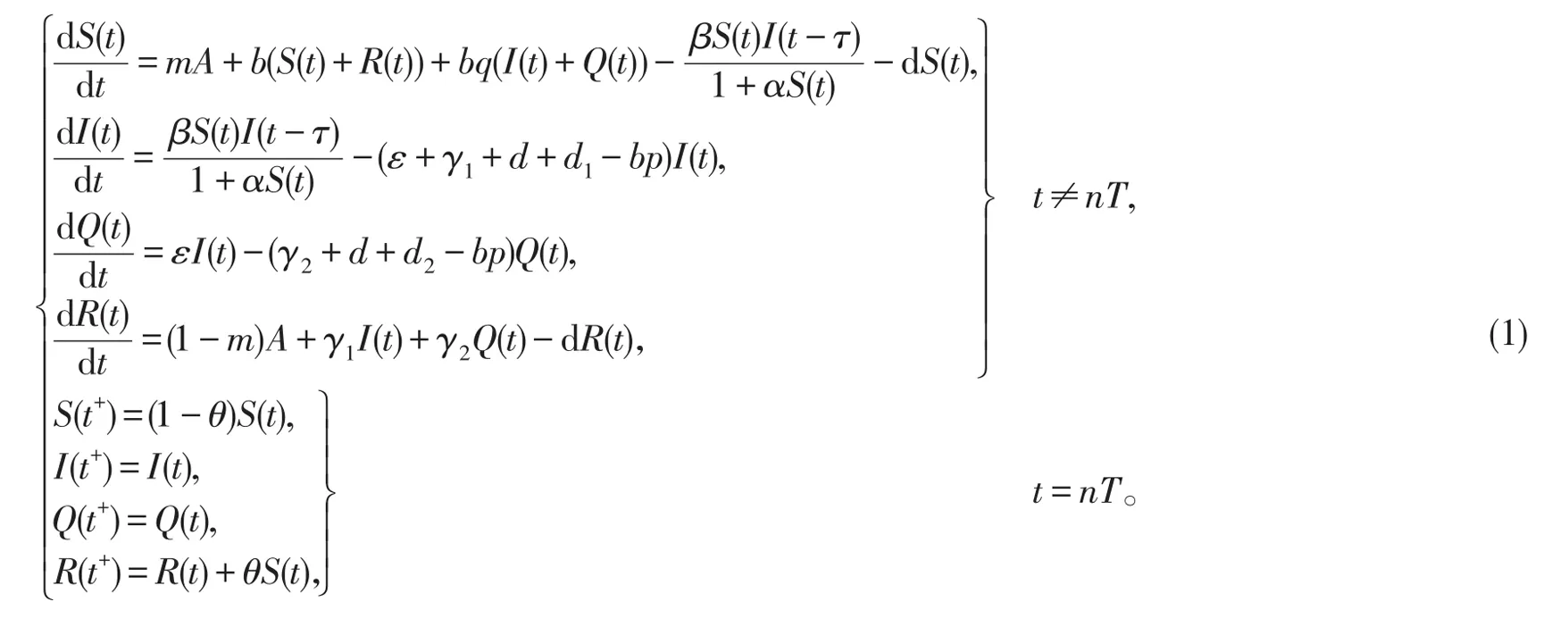
设S(t),I(t),Q(t),R(t)分别为t时刻易感者的数量,染病者的数量,隔离者的数量,恢复者的数量。A为外来人口的输入率,mA和(1-m)A分别为t时刻输入易感者和已获得免疫的移出者的数量(且0＜m≤1)。p为垂直传染率( )p+q=1,b,d分别为t时刻出生率与死亡率(且d＞b),ε为隔离率,γ1,γ2分别为未隔离病人的移出率和隔离病人的移出率,d1,d2分别为染病者因病死亡率和隔离者因病死亡率。τ为染病者能感染易感染者的滞后时间,θ(0≤θ≤1)为预防接种率,而N(t)=S(t)+I(t)+Q(t)+R(t),T为脉冲周期,这里p,b,d,ε,γ1,γ2,d1,d2,τ均为正常数。

总人口的微分方程为

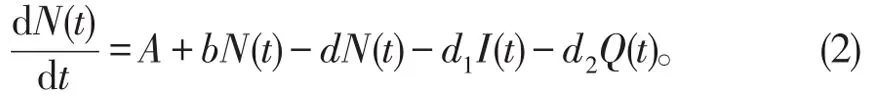
t≠nT, 由(2)得

由常微分方程的比较定理有:

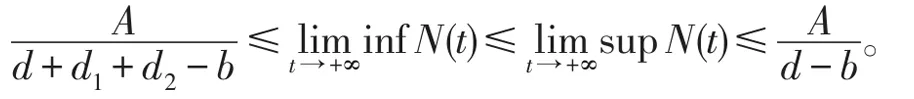
考虑生态意义,初始函数满足以下条件:

在文中,我们采用以下记号:

2 无病周期解的全局吸引性

引理1脉冲微分方程组

存在唯一的全局渐近稳定周期解，

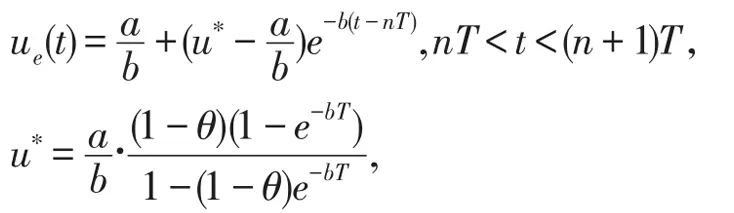
其中a＞0,b＞0,0＜θ＜1。

引理2时滞微分方程

当a＞0,b＞0,τ＞0,且对于t∈[-τ,0],有(i)当a＜b时,则当a＞b时,则

在文中,讨论系统(1)的无病周期解的存在性,此时系统(1)不存在染病者,即I(t)=0,t≥0。由系统(1)的第三个方程知当I(t)=0时,有

由以上条件知,系统(1)必须满足

从而由引理1和(5)式有

易知系统(4)有唯一周期解(Se(t),0,0,其中

因此,系统(1)的无病周期解为

定义基本再生数

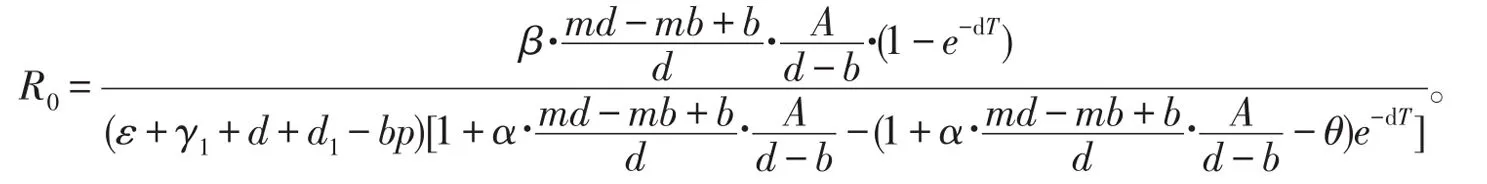
引理3当d＞b时,系统(1)的所有正解一致有界。

证明设(S(t),I(t),Q(t),R(t))是系统(1)的任一正解,则N(t)=S(t)+I(t)+Q(t)+R(t)满足:

由脉冲微分不等式,得:

因此,存在一个常数M＞0,当t充分大时,N(t)≤M,从而S(t)≤M,I(t)≤M,Q(t)≤M,R(t)≤M,所以系统(1)的所有正解一致有界。

定理1 若d＞b且R0＜1,系统(1)的无病周期解是全局吸引的。

证明当d＞b且R0＜1时,取一个充分小的ε0＞0,使得

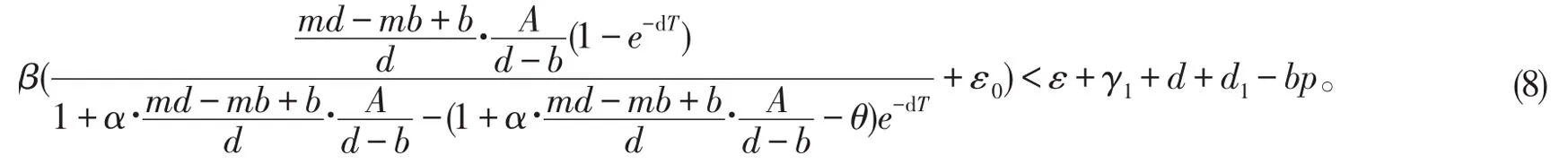
由系统(4)的第一个方程可得

考虑下面的比较系统

由引理1可知(10)的周期解

是全局渐近稳定的,其中

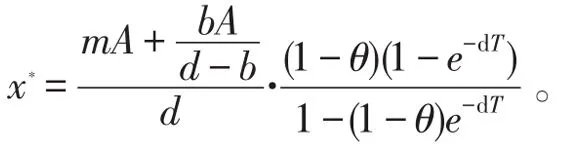
令(S(t),I(t),Q(t),R(t))是系统(1)满足初始条件S(0+)=S0＞0的解,x(t)是系统(10)满足初始条件x(0+)=S0的解。由脉冲比较定理知,存在n1＞0,使得S(t)＜x(t)＜xe(t)+ε0,nT＜t≤(n+1)T,n＞n1。即

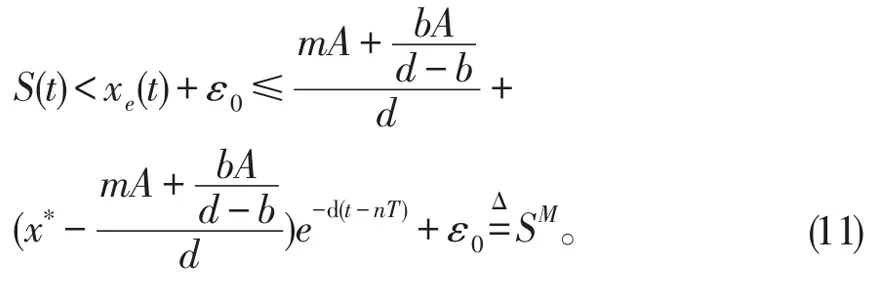
由系统(1)的第二个方程,可知

考虑下面的比较方程

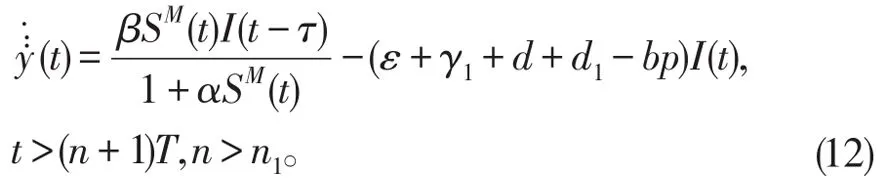
令(S(t),I(t),Q(t),R(t))是系统(1)满足初始条件(3),I(θ)=ϕ(θ)(θ∈[0,τ])的解。y(t)是(12)满足初始条件y(θ)=ϕ(θ)(θ∈[0,τ])的解。由比较定理和I(t)的非负性知

所以对于充分小的ε1＞0,存在n2＞n1,(n2T＞(n1+1)T)使得对所有的t＞n2T有

由系统(1)的第三个方程,可知n3＞n2,使得

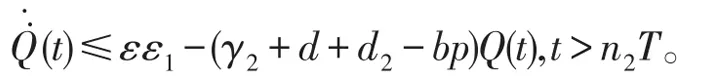
由(2)知,

当t＞n3T且n＞n3时,考虑下面的比较系统

由引理1可知(16)的周期解

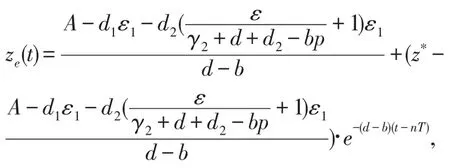
nT＜t≤(n+1)T,是全局渐近稳定的,其中

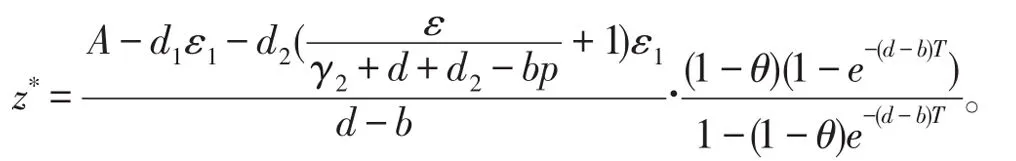
易知

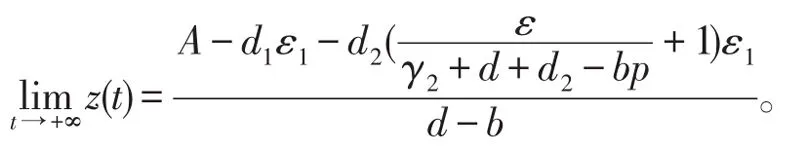
由比较定理存在一个整数n4＞n3,当t＞n4T时,使得

又知ε1是任意小的且和(17)可知

由 (13),(18),存在n5＞n4,使得对

由系统(1)的第一个方程和式(14),(15),(18)可得:

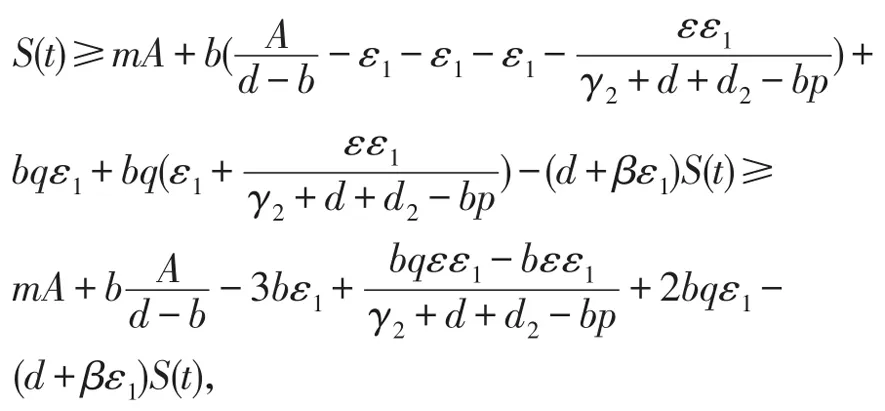
当t＞n5T时,考虑下面的比较系统，

由引理1可知(20)的周期解

是全局渐近稳定的,其中

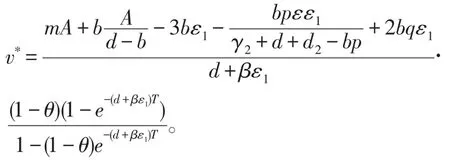
易知

由脉冲比较定理知存在一个整数n6＞n5,使得

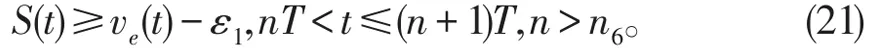
因为ε1充分小,由(9),(21)可得:

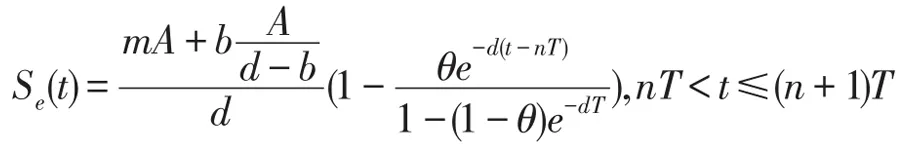
是全局吸引的,即

由(13),(18),(22)和

推论 (I)如果βc＞(ε+γ1+d+d1-bp)(1+αc)时,假 如θ＞θ∗或 者T＜T∗,无病 周 期解 (Se(t),0,0,是全局吸引的;(其中

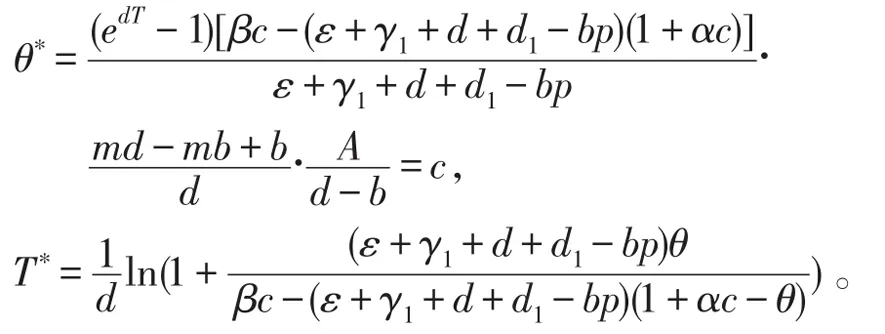
(II)如果βc≤(ε+γ1+d+d1-bp)(1+αc)时,无病周期解是全局吸引的。

注:定理1说明了当R0＜1,系统(1)的无病周期解是全局吸引的,推论说明了脉冲接种率足够大或脉冲接种间隔时间足够短时甲肝传染病将会消失。