液态镓在石墨烯表面的润湿性及形貌特征∗

王俊珺 李涛 李雄鹰 李辉†

1)(山东大学,材料液固结构演变与加工教育部重点实验室,济南 250061)2)(昌吉学院物理系,昌吉 831100)

(2017年12月22日收到;2018年5月3日收到修改稿)

液态Ga及其合金的熔点低、毒副作用小、导电率高,使得这类液态金属能像石墨烯一样被广泛应用于微流器件、柔性电子器件中,制备这些器件的关键在于有效控制各生产环节中液态金属在固体界面上的润湿性及形貌特征.基于Lennard-Jones(L-J)势函数,利用分子动力学模拟方法研究了金属Ga在石墨烯表面的润湿性,根据模拟结果拟合的L-J势参数能正确描述Ga原子与衬底之间的相互作用并得到了与实验值极为接近的润湿角,发现衬底与液膜间相互作用的微小改变都会对最终润湿形态产生极大影响,平衡态的润湿角和脱离衬底速度随着Ga-C间势能的减小而增大,并成功获得了不同厚度的Ga液膜在石墨烯表面的形态演变规律,极为符合液态Ga的基本特性.利用所得L-J势函数参数模拟了液态Ga在粗糙度相同但纳米柱尖端形貌不同的C材料表面的润湿演变,发现纳米柱尖端形貌对液态Ga的润湿过程及状态影响极大.

1 引 言

润湿性是材料的基本性质,迄今为止人类研究固液表面的润湿性已有上百年的历史[1,2].材料的润湿性是由持续接触的固液材料之间的相互作用所引起的,这是一种长程的弱相互作用,微小的改变都会展现出不同的润湿状态.有效控制液体的铺展和固体表面的润湿状态是一个很重要的研究领域,其结果不仅影响着人类对自然界的认知,也关乎着人类生产生活的方方面面.研究固体表面的润湿性不仅对于自清洁材料、防水材料、防污染材料的制备,热能系统效率的提高,以及流体摩擦力的减少等都具有重要的理论价值和实际意义,而且与3D打印、焊接、铸造、冶金、薄膜及封装技术等密切相关[3−7].

随着器件精密化、微型化的发展趋势,形状可变但属性变化不大的液体填充柔性器件备受关注.石墨烯的发现使获得一种具有原子级别厚度的、透明且灵活的电子器件成为可能[8].碳纳米管和石墨烯基于本身出色的高导电性,良好的热稳定性.强大的机械弯曲性能、化学惰性以及越来越低的造价,为制备柔性电子器件提供了独一无二的机会.但碳纳米材料缺点很多,如石墨烯易起褶皱、开裂、卷曲,使得表面电阻不够稳定,而液态金属和石墨烯等碳纳米材料组成的闭路连接能够很好地弥补这些缺点,并且在发生形变时保持原有的物理属性[9−11].常温金属镓的熔点低至29.76◦C,其毒副作用小、黏度低、蒸气压也较低,并具有极高的导电率(3.4×106S/m)[12],几乎高于铜一个数量级,并可通过与其他金属掺杂成合金来灵活调谐各种功能参数[13],比如一种镓铟锡合金(68.5%Ga,21.5%In及 10%Sn)液相的温度可低至−19◦C.镓及其合金优良的物理性能引起了科学家们的极大关注,可灵活操控其形状来制备微流器件和柔性电子器件[9−11,14,15]等,比如Ga-In合金嵌入弹性体薄膜中,可作为自由伸缩的电线或实时响应变形阻力变化的压力传感器[14,15].而在把液态金属制成合格电子产品的过程中,从液态金属的制备到液态金属的分封,有效控制液态金属与各种固态表面之间的润湿性极为关键.控制液态金属润湿性的方法很多,例如改变液态金属成分及形状、衬底材质及结构、系统状态(温度、压强、场强)等.清华大学刘静教授课题组[16]通过外加电场极大地改变了液态Ga合金的表面张力,发现液态Ga合金可在10 V左右的低电压作用下发生液滴之间的自动融合—断裂—再合并等行为,并将一面积很大的金属液膜在数秒内收缩为单一金属液球,从而使表面积改变高达上千倍,变形过程极为迅速.Fuentes-Cabrera等[17]成功利用Lennard-Jones(L-J)势研究了液态铜在石墨表面的润湿状态,发现L-J势的取值影响着铜液滴的润湿形态.

目前采用模拟方法研究液态Ga在石墨烯表面上的润湿性非常少,因此本文利用分子动力学模拟方法研究液态Ga在碳纳米材料表面的润湿性及形态演变,尝试利用L-J势来描述液态Ga在石墨烯表面润湿性,以及探讨通过修饰石墨烯表面来改变液态Ga的润湿性的可能性.

2 模型与计算方法

本文利用LAMMPS(largescale atomic/molecular massively parallel simulator)软件进行计算[18].在宏观正则系综(NVT)下利用分子动力学模拟方法,使用Nose-Hoover方法控制系统的温度,采取velocity-verlet算法求解动力学方程,时间步长设为 1.0 fs(1 fs=10−15s),总时长为200 ps(1 ps=10−12s),温度均为1000 K,利用修正型嵌入原子法(MEAM)势函数来模拟Ga原子间的相互作用[19,20],用AIREBO势函数计算C-C相互作用[21],使用 12-6 L-J势函数来描述金属Ga和C之间的相互作用.L-J势函数有一大优势,那就是可以通过改变势阱深度来描述不同的体系.如文献[22—24]就通过简单地改变势阱深度成功获得了从润湿到不润湿的模拟结果.受这些工作的启发,使用相似的方法,参考Li等[25]第一性原理的计算工作,得到黏附直径σ=0.318 nm,势阱深度ε分别取为0.5,0.1,0.01,0.007,0.005,0.004 eV,模拟了Ga液膜(半径为13.5 nm,层厚为2 nm)在25 nm×25 nm的石墨烯(a=0.2462 nm,c=0.67079 nm,双层,底层固定)上的润湿特性.其次,根据液态Ga在石墨表面上实验测出的润湿角(127◦)[26],拟合出最佳势阱深度,并据此分别模拟了厚度分别为1,2,3 nm的Ga液膜(半径为13.5 nm)的润湿性.最后,模拟了层厚为2 nm的Ga液膜在用三种等高等底的碳纳米柱修饰的石墨烯面上的润湿.三种碳纳米柱分别是(5,5)CNT(carbon nanotubes),(5,5)CCNT(caped carbon nanotubes),CNC(carbon nanocone,旋移角为240◦)(如图1所示),高度均为1 nm,底面直径为0.678 nm,两两柱底间距离均为0.34 nm.在所有的模拟条件下,初始Ga液膜与衬底的最短垂直距离均为0.2 nm.此外,Ga液膜是取自1000 K平衡态下的块体的Ga熔体.模拟图片由OVITO软件读取生成[27].

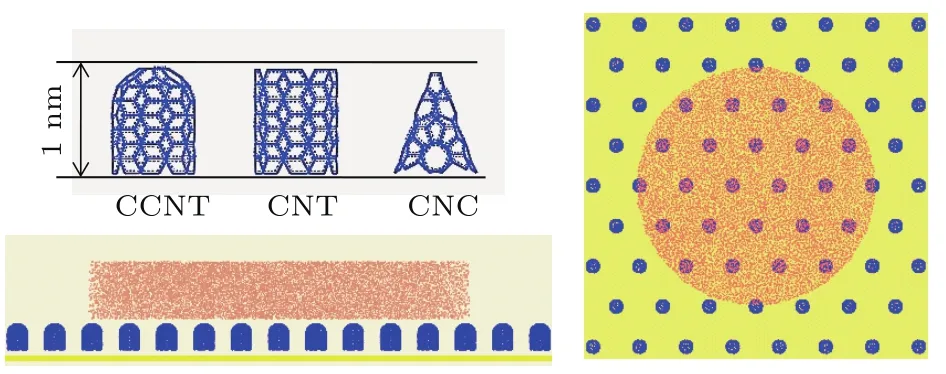
图1 纳米柱修饰的石墨烯衬底(其中,肉粉色的是镓,蓝色的是纳米柱,黄色的是石墨烯)Fig.1.Three types of graphene substrate modified with nanorads(gallium is pale dogwood,nanopillars is blue and grapheme is yellow).

3 结果与讨论

3.1 L-J势的势阱深度对液滴润湿状态的影响

分别取势阱深度ε为0.5,0.1,0.01,0.007,0.005及0.004 eV,通过分子动力学(MD)模拟,可测得Ga液膜在石墨烯表面上平衡态时的润湿状态(如表1所列).当ε=0.5 eV时,Ga液膜迅速变薄完全铺展在石墨烯上,并引得未完全固定的石墨烯边缘卷起并包覆Ga液膜,表明此时Ga-C间相互作用过大,不仅使得Ga液膜与石墨烯完全润湿,还使得上层石墨烯外围脱离了底层的束缚.当ε=0.1 eV时,Ga液膜8 ps左右在石墨烯表面铺展开(如图2(a)所示),未完全固定的石墨烯边缘有些许卷起,结果与实验相差极大.当ε=0.01 eV时,Ga液膜在石墨烯面上呈倒扣的碗状,润湿角为78.4◦,并且石墨烯边缘微微卷起(如图2(b)所示).继续降低势阱深度为0.007 eV时,Ga液膜呈现出不润湿的状态,润湿角为112.3◦,但与实验值相比仍偏小.继续减小势阱深度,令ε=0.004 eV时,平衡态时Ga液膜润湿角为136.9◦,对比实验测得的1050◦C时液膜Ga在石墨上的润湿角值(127◦),发现稍显偏大.进而小幅度增加势阱深度,取ε=0.005 eV,发现平衡态时其润湿角为129.6◦,最为接近实验测值(127◦).因此在之后的模拟中势阱深度ε均取固定值0.005 eV.

虽然每次长程L-J势能改变量只有10 meV,但这种微小变化对液态金属最终的润湿状态及液膜边缘的收缩速度及垂直表面的脱离速度都有显著影响,然而润湿过程却又是相似的.首先,由于初始状态的Ga液膜底端距衬底仅为0.2 nm,而Ga-C间的黏附直径为0.318 nm,在Ga液膜中受到衬底吸引力的原子远多于受到排斥力的原子,因此在衬底的影响下Ga液膜整体有向下运动的趋势.与此同时,Ga液膜内部原子在衬底外力的影响下重新排布,表面原子形成新的表面张力,从而使得Ga液膜边缘收缩,继而液膜层高变薄,如图2所示,在垂直于衬底方向可以观察到液膜局部会出现空洞.在液膜逐渐演化的过程中,Ga原子受原子间短程强相互作用影响,积聚在一起,克服向下的惯性力,液膜空洞逐渐消失,层高变厚,边缘继续收缩,逐渐变成倒扣的半实心球状液滴.随着Ga-C间的相互作用逐渐变为以排斥力为主导,当L-J势的排斥能达到极大值时将完全抵消向下的运动趋势,并使得Ga液滴开始反弹继而远离衬底,在上升过程中衬底对液滴的作用逐渐由排斥变为吸引.此后,Ga液滴在衬底上将处于反复回弹振荡状态,且振荡幅度越来越小.

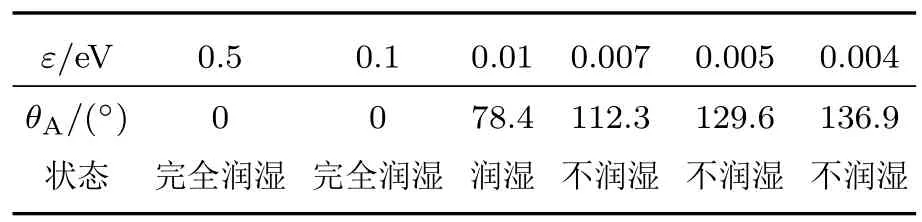
表1 Ga液膜在石墨烯表面润湿角及润湿状态随势阱深度变化Table1.Variation of contact angles and wettabilities with Different well depths.

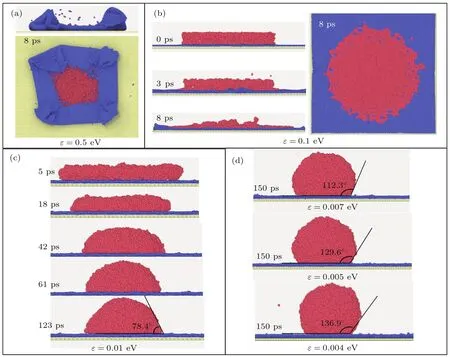
图2 势阱深度对Ga液膜在石墨烯上的形貌演变的影响 (a)ε=0.5 eV;(b)ε=0.1 eV;(c)ε=0.01 eV;(d)ε=0.007,0.005,0.004 eVFig.2.Effects of ε on the wetting morphology of Ga nano films on graphene surfaces:(a) ε =0.5 eV;(b)ε=0.1 eV;(c)ε=0.01 eV;(d)ε=0.007,0.005 and 0.004 eV.

3.2 液膜层厚对润湿状态的影响

本文选取半径均为13.5 nm,层厚分别为1,2,3 nm的圆盘状Ga液膜来研究厚度对液滴形态演变的影响.基底仍然选用石墨烯,其他模拟条件不变.图3给出了不同厚度的Ga液膜在石墨烯上随着时间的演化状态.当系统达到平衡状态时,初始厚度分别为1,2,3 nm的液膜所对应的最终润湿角依次为127.3◦,129.6◦,131.4◦.由图3(a),(b)可以看出液膜越薄,Ga液膜状态演化的越快,液膜边缘的收缩速度及反弹速度也更快.在8 ps时,1 nm的Ga液膜出现的孔洞远多于其他两种层高的液膜,并且在这时三种液膜平行于底面方向的直径相差不大.此后,随着时间的进程,由于受衬底影响的原子占总原子数比例最高,1 nm的Ga液膜的孔洞最晚消失,层高和平行于底面方向的直径都是最小.由图3(d)和图3(e)可以看出(其中EL-J为固液间相互作用能,vz为液滴在z方向上的质心速度),由于固液接触的初始面积相同,固液间的相互作用势相差不大,层厚为1 nm的Ga液膜与衬底间的相互作用势能略小,而2,3 nm的液膜与衬底间的相互作用势能基本相同.但各液膜的粒子数相差较大,因此由衬底所引起的向下运动的初始速度相差较大,厚度为1 nm的液膜的速度大小约是厚度为2 nm的液膜速度的2倍,是厚度为3 nm的液膜速度的近4倍.厚度为1 nm的Ga液膜与衬底的排斥作用达到极大值的时间最早,因此也以最快的速度向上反弹,而厚度为3 nm的Ga液膜出现反弹现象的时间最晚.如图3(c)所示,50 ps后,厚度为3 nm的Ga液膜与衬底间的相互作用明显大于厚度为1,2 nm的Ga液膜与各自衬底间的相互作用,并且100 ps后,如图3(c)所示,有

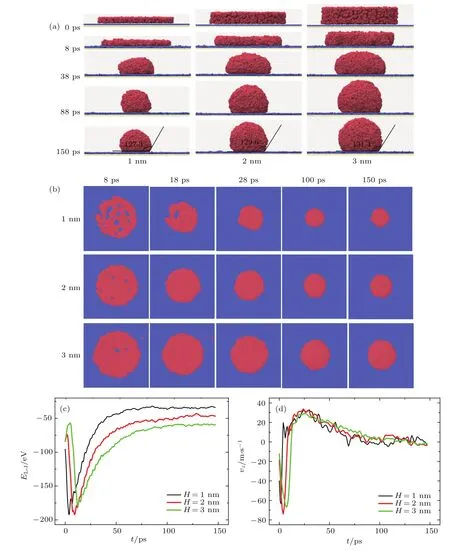
图3 不同层厚Ga液膜在石墨烯上的形态演变 (a)x-z面(侧面)的形态演变;(b)x-y面(俯视面)的形态演变;(c)Ga-C相互作用能演化;(d)Ga液膜在垂直方向上的速度演化Fig.3.Morphological evolution of Ga nano films with Different thickness on the graphene surfaces:(a)Evolution of x-z profile;(b)evolution of x-y profile;(c)Ga-C interaction versus wetting time;(d)retraction velocity of Ga nano film in vertical direction.

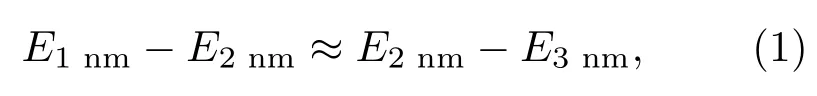
式中E1nm,E2nm,E3nm分别为厚度为1,2及3 nm的Ga液膜与各自衬底间的相互作用,这说明Ga液膜与衬底间势能变化量非常接近.由于在Ga原子间的强相互作用影响下,Ga液膜内部原子重排,衬底为液滴提供的动能一部分转换成表面能,另一部分被与衬底的摩擦耗散掉.已有研究表明,原子数越多形成新的表面张力所耗能量就越多,而厚度越大与衬底的摩擦耗散也就越多,这使得液膜厚度越大,其横向收缩速度及幅度越小,最终使得液膜与石墨烯的接触面积也就越大,并且从图3(c)可以看出这种影响与厚度是成比例的,因此其对液滴的最终影响相似,表现在液滴最后的速度均值(如图3(d)所示)及润湿角(如图3(a)所示)相差不大.这种规律与实验结果相似,这进一步证明本文所取的L-J势函数能够很好地描述液态Ga在石墨烯上的润湿特性.

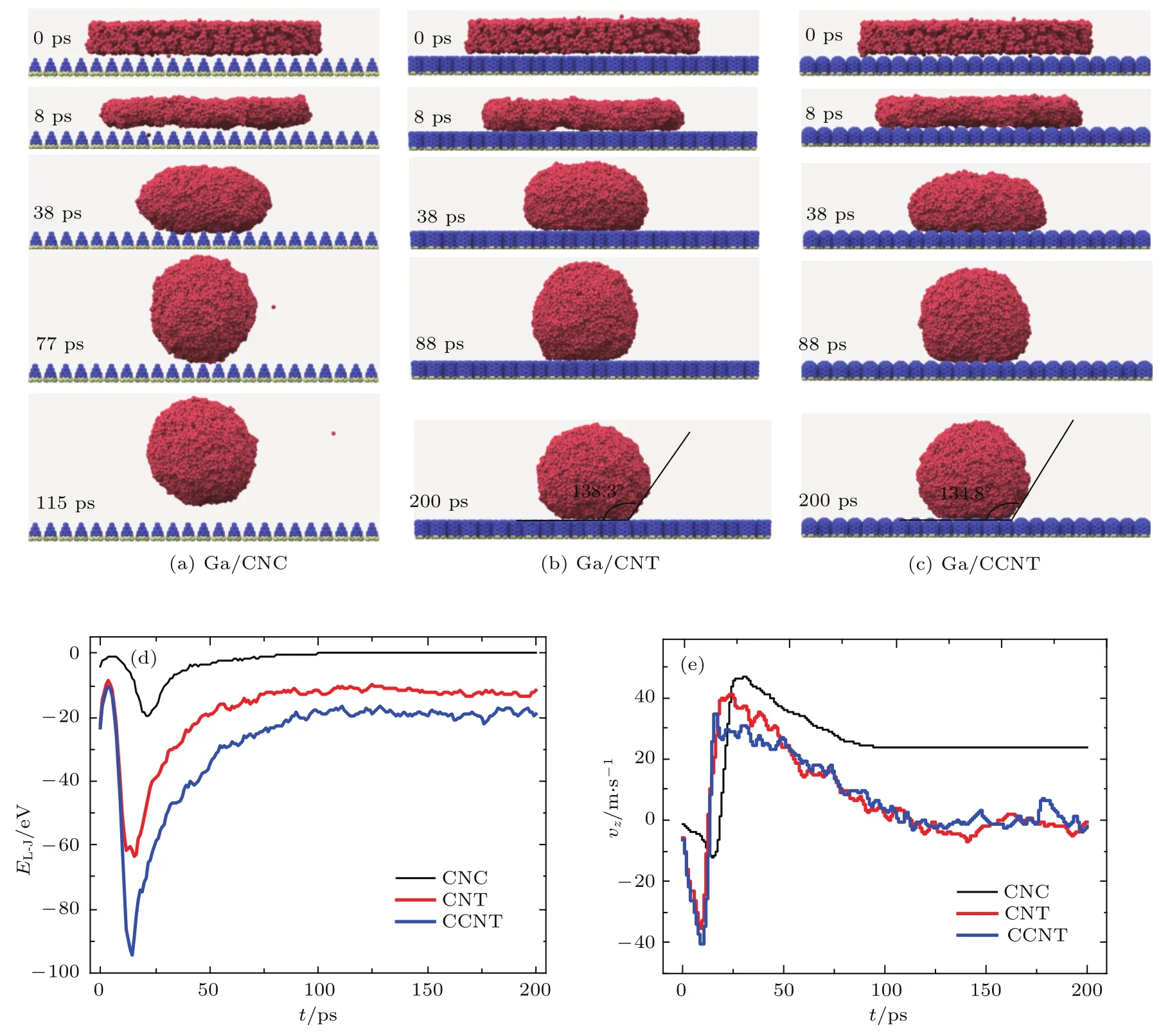
图4 Ga液膜在用不同碳纳米柱修饰的石墨烯上的润湿形态 (a)Ga/CNC;(b)Ga/CNT;(c)Ga/CCNT;(d)Ga-C相互作用;(e)Ga液膜在垂直方向上的速度变化Fig.4.Morphological evolution of Ga nano films on three types of graphene surfaces modified with nanorads:(a)Ga/CNC;(b)Ga/CNT;(c)Ga/CCNT;(d)Ga-C interaction versus wetting time;(e)retraction velocity of Ga nano film in vertical direction.

3.3 衬底粗糙形貌对润湿状态的影响

为了进一步理解粗糙表面对液滴润湿性的影响,本文研究了用不同尖端形貌碳纳米柱修饰的石墨烯衬底对液膜润湿演变的影响.选取厚度2 nm、半径13.5 nm的Ga液膜,分别将其放在粗糙度相同、但柱尖端形貌不同的三种石墨烯衬底上,衬底上任意最近邻两柱底间距离均为0.34 nm,为理论上所能取得的最小距离.由图4可知,液滴在这三种衬底上的润湿过程和最终的润湿状态差异很大.Ga液膜在碳纳米管CNT和带帽碳纳米管CCNT衬底上呈不润湿状态,稳定态的润湿角分别为138.3◦和134.8◦,均大于Ga液膜在石墨烯表面上的润湿角,而在碳纳米锥CNC衬底上,Ga液膜最终呈现的是反润湿状态,100 ps后完全脱离了衬底束缚,以球状匀速远离衬底.与Ga液膜在CCNT衬底上相比,Ga液膜在CNT衬底沿垂直方向的初始速度和边缘的收缩速度都更大一些.润湿状态取决于液体与固体表面之间相互作用的强弱,处于L-J势能影响范围的粒子数多少影响着固液相互作用的强弱.显然碳纳米锥CNC的尖端形状使其影响液态Ga的C原子数最少,而CCNT中影响液态Ga的C原子数最多.因此从图4(d)可以看出,初始状态下Ga液膜与CNC衬底间的相互作用能最小,Ga液膜与CCNT衬底的相互作用能最大,使得CCNT衬底对Ga液膜的束缚也最大.于是较其他两种衬底,Ga液膜在初始阶段的下沉速度最大,与CCNT衬底间的所能达到的垂直距离最小,进而使得Ga-C间的排斥极大值也最大,之后反弹阶段Ga液膜能获得反弹加速度越小,最终使得平衡状态下受到衬底束缚的原子数也更多,润湿角也更小.

4 结 论

本文利用分子动力学模拟方法探究了金属镓(Ga)在石墨烯表面的润湿性,获得了能准确描述原子间相互作用的Lennard-Jones(L-J)势函数参数,计算得到的润湿角与实验值极为接近.并运用合适的参数研究了液膜层厚、衬底的粗糙度及形貌对液膜润湿性及形态演变的影响,取得了如下结论.

1)L-J势函数的势阱深度对Ga液膜在石墨烯表面的润湿状态有显著影响.随着势阱深度的减小,液膜在衬底表面由完全润湿态逐渐变为不润湿态.

2)Ga液膜的厚度显著影响其润湿形貌的演变.随着液膜厚度的减小,初始状态液滴沿垂直于衬底方向的速度和衬底边缘的收缩速度都会变大,但最终的润湿角及速度值相差不大,这与实验相符.

3)在相同粗糙度时,修饰衬底的纳米柱尖端形貌对Ga液膜润湿行为有非常重要的影响.Ga液膜在CNC衬底上出现反润湿现象,而在CNT和CCNT衬底上没有出现反润湿特征,还表现出了略有差异的不润湿特性.表明通过纳米柱修饰石墨烯.是调谐液态Ga的润湿性的一种有效方法.但是纳米柱尖端形状造成液态Ga润湿性差异巨大的原因还需进一步探讨.