半导体激光器输出混沌光的延时特性和带宽∗

李增 冯玉玲 王晓茜 姚治海

(长春理工大学物理系,长春 130022)

(2018年1月5日收到;2018年3月23日收到修改稿)

提出一个新的方案用于抑制半导体激光器输出混沌光的延时特性并研究其带宽.在该方案中,将由伪随机信号驱动的相位调制器加到具有双路光反馈的半导体激光器的两个反馈腔中,从而构成具有双路相位调制光反馈的分布反馈半导体激光器系统.数值研究了延迟时间和反馈系数等参数对该系统输出混沌光的延时特性的影响,用自相关函数曲线中的延时特征峰的最大值表示延时特性.然后将该系统对延时特性的抑制效果和具有双路光反馈的分布反馈半导体激光器系统以及具有单路相位调制光反馈的分布反馈半导体激光器系统进行比较,结果表明本文所提出方案的抑制效果最好.进而基于能有效抑制延时特性的参数条件研究了具有双路相位调制光反馈的分布反馈半导体激光器输出混沌光的带宽,结果表明,抽运因子的增大和反馈系数的增加都能使系统输出混沌光的带宽变大.

1 引 言

分布反馈半导体激光器(distributed feedback semiconductor lasers,DFB-SL)在有光反馈或外光注入等扰动下能够输出混沌激光,可以广泛应用在高速保密通信[1]、高速真随机数的产生[2,3]、混沌激光雷达[4]和光时域反射仪[5]等方面.目前外腔反馈半导体激光器能输出高维度的混沌激光,因此被认为是最好的混沌熵源之一[6−9].但是激光在外腔的往返过程,在输出混沌光的自相关函数曲线中产生明显的外腔延时特征(time delay signature,TDS)峰,这对混沌激光的应用产生负面影响.例如基于混沌激光作为物理熵源的高速真随机数发生器,TDS的出现表示混沌激光中出现了弱周期性,从而降低了混沌激光的无序性,使生成的高速真随机数的统计性能变差[2].DFB-SL的中心波长是1550 nm,正处于光纤通信的最低损耗窗口,其输出混沌光的高带宽和低自相关特性(即低的延时特性)使其被广泛应用于保密通信和真随机数发生器等领域,因此抑制其输出混沌光的延时特性并提高其带宽成为研究热点.Rontani等[10]通过调节偏置电流数值研究了半导体激光器输出混沌光的TDS.Wu等[11,12]实验研究了相干和非相干单光反馈半导体激光器的TDS.Lee等[13]用两个反馈腔来增加系统的复杂度,从而抑制了TDS.Wang等[14]通过延时自干涉的方法提高半导体激光器输出混沌光带宽的同时抑制其TDS.Lu等[15]对于具有滤波光反馈的半导体激光器,数值研究了其输出混沌光的TDS.Xiang等[16]数值研究了相位调制光反馈对半导体激光器输出混沌光的TDS的抑制.Wu等[17]数值研究了双路光反馈对半导体激光器输出混沌光的TDS的抑制.Wang等[18]利用外光注入的方法提高光反馈半导体激光器输出混沌光的带宽.本文提出在具有双路光反馈的半导体激光器(semiconductor laser with double op-tical feedback,SL-DOF)的两个反馈腔中分别加入一个用伪随机信号驱动的相位调制器进而构成具有双路相位调制光反馈的半导体激光器(semiconductor laser with double phase modulated optical feedback,SL-DPMOF),研究其输出混沌光的TDS和带宽,进而证明该方案能有效地抑制半导体激光器输出混沌光的TDS,并在有效地抑制TDS的参数条件下给出了系统输出混沌光的带宽随其参数的变化规律.

2 理论模型

本文提出的具有双路相位调制光反馈的分布反馈半导体激光器的结构示意图如图1所示.

在图1中,DFB-SL发出的激光首先经过光纤耦合器FC1分成两束,之后一束通过光纤耦合器FC2又分成两束,分别通过可调光衰减器VOA1和VOA2、相位调制器PM1和PM2以及光纤反射镜FR1和FR2再反馈回DFB-SL中.这里分别利用两个任意波发生器AWG1和AWG2产生的伪随机信号驱动两个相位调制器,从而改变反馈光的相位并消除外腔延时特性;从耦合器FC1输出的另一束光经过光隔离器ISO后,利用光电探测器PD转换成电信号,输入到示波器OSC中.图1所示的半导体激光器系统的动力学方程如下[19]:

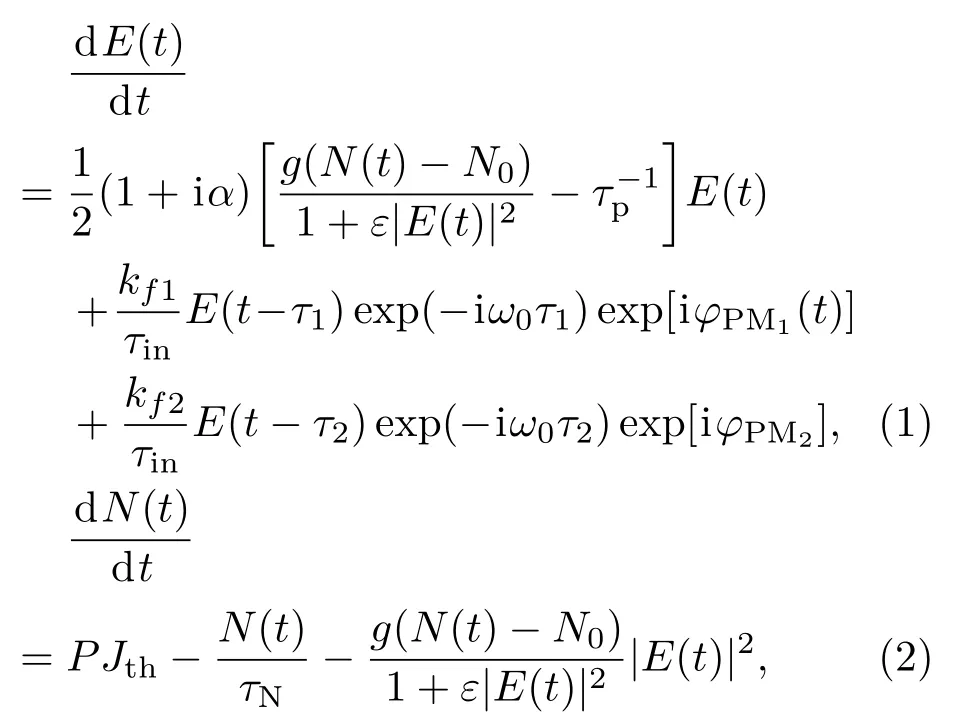
其中E(t)是激光器的慢变电场复振幅;N(t)是载流子数密度;α是线宽增强因子;ω0是激光器的中心场频率;g是微分增益系数;N0是透明载流子数密度;ε是饱和增益系数;τp是光子寿命;τN是载流子寿命;P是抽运因子;Jth为阈值电流密度,且Jth=Nth/τN,Nth=N0+1/(gτp); τin是激光在腔内的往返时间;脚标1和2分别代表反馈腔1和反馈腔2,τ1和τ2分别是两个反馈腔的延迟时间,kf1和kf2分别是两个反馈腔的反馈系数;φPMi(i=1,2)分别是两个相位调制器(PMi)产生的相移,并且φPMi= πVRFifmi(t)/Vπi(i=1,2),VRFifmi(t)是任意波信号发生器(AWGi)加在相位调制器(PMi)上的调制电压,Vπi是相位调制器(PMi)的半波电压.

图1 具有双路相位调制光反馈的分布反馈半导体激光器系统的结构示意图Fig.1.Schematic diagram of the distributed feedback semiconductor lasers with double phase modulated optical feedback.

本文利用的自相关函数(autocorrelation function,ACF)定义为[20]:

(3)式中I(t)为激光器输出光的强度,∆t为移动时间,表示对时间求平均.利用系统输出光的自相关函数曲线中延时特征峰的最大峰值β来定量描述输出混沌光的延时特性.一般认为β<0.2时,混沌激光就无弱周期性,即TDS被较好地抑制了[20].

3 TDS的数值研究和分析

3.1 延迟时间τ1对TDS的影响

参数取值如下[21]:α= 5.0,g=8.4×10−13m3·s−1,N0=1.4 × 1024m−3,τp=1.927 ×10−12s,τin=8.0× 10−12s,τN=2.04× 10−9s,ε=2.5 × 10−23,P =1.6,kf1=kf2=0.1,B1=B2=B=1.0,τ2=3.0 ns,以τ1作为控制参数,利用四阶-龙格库塔法对(1)式和(2)式进行数值求解,得到τ1=2.08,2.48,2.88 ns这3个值时系统输出激光强度的时间序列和对应的ACF曲线如图2所示.

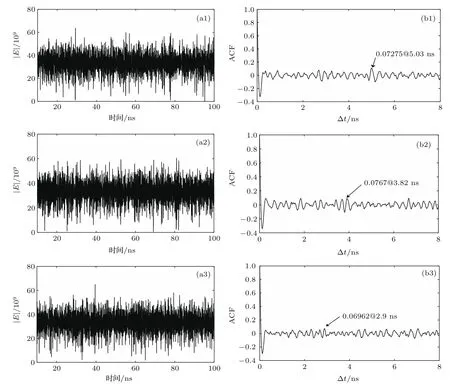
图2 DFB-SL-DPMOF在不同的延迟时间τ1下输出混沌激光的时间序列(a1)—(a3)以及对应的ACF曲线(b1)—(b3)(a1)—(b1) τ1=2.08 ns;(a2)—(b2) τ1=2.48 ns;(a3)—(b3) τ1=2.88 nsFig.2.Time series(a1)–(a3)and the corresponding ACF curves(b1)–(b3)of chaotic laser from DFB-SL-DPMOF with Different delay time τ1:(a1)–(b1) τ1=2.08 ns;(a2)–(b2) τ1=2.48 ns;(a3)–(b3) τ1=2.88 ns.

由图2(a1)—(a3)可见,光强的幅值随时间的变化呈无规则的起伏状态,这表明此时半导体激光器输出的是混沌激光;图2(b1)—(b3)中,左边第一个尖峰几乎和纵轴重合,这个尖峰是由弛豫振荡引起的[14],其余尖峰中的最高尖峰及其峰值(即延时特征值β)已经在图中标出,可见β值都小于0.2,即输出混沌光的TDS被有效地抑制了.为了进一步显示系统输出混沌光的β值随延迟时间τ1的变化,数值求解(1)式和(2)式,得到拟合平滑后的延时特征值β随τ1的变化趋势曲线,如图3所示.

图3 延时特征值β随延迟时间τ1的变化Fig.3.Variation of the time delay characteristic values β with the delay time τ1.

由图3可见,在所选的τ1的取值范围内,随着τ1的逐渐增大,β值有起伏地变化,当τ1=2.88时,β值为最小,所以图3所示的β值随τ1的变化情况和图2(b1)—(b3)是相符的,即图2(b3)(对应的τ1=2.88 ns)对TDS的抑制效果最好,这是由于此时两个反馈腔的延时差τ2−τ1=0.12 ns≈(1/2)τro, τro(=2π(gE2/τp)−1/2)为激光器的弛豫振荡周期[14,15,17].

利用对TDS有较好抑制效果(图2的(b3))的参数条件,下面进一步研究调制深度B对TDS的影响.

3.2 调制深度B和反馈系数kf1以及抽运因子P对TDS的影响

首先取抽运因子P=1.6,其他参数的取值与图2(b3)相同,数值求解(1)式和(2)式,得到图4(a)所示的延时特征值β随参数B和kf1变化的二维图.然后取反馈系数kf1=0.1,其他参数的取值与图2(b3)的相同,数值求解(1)式和(2)式,得到图4(b)所示的延时特征值β随参数B和P变化的二维图.

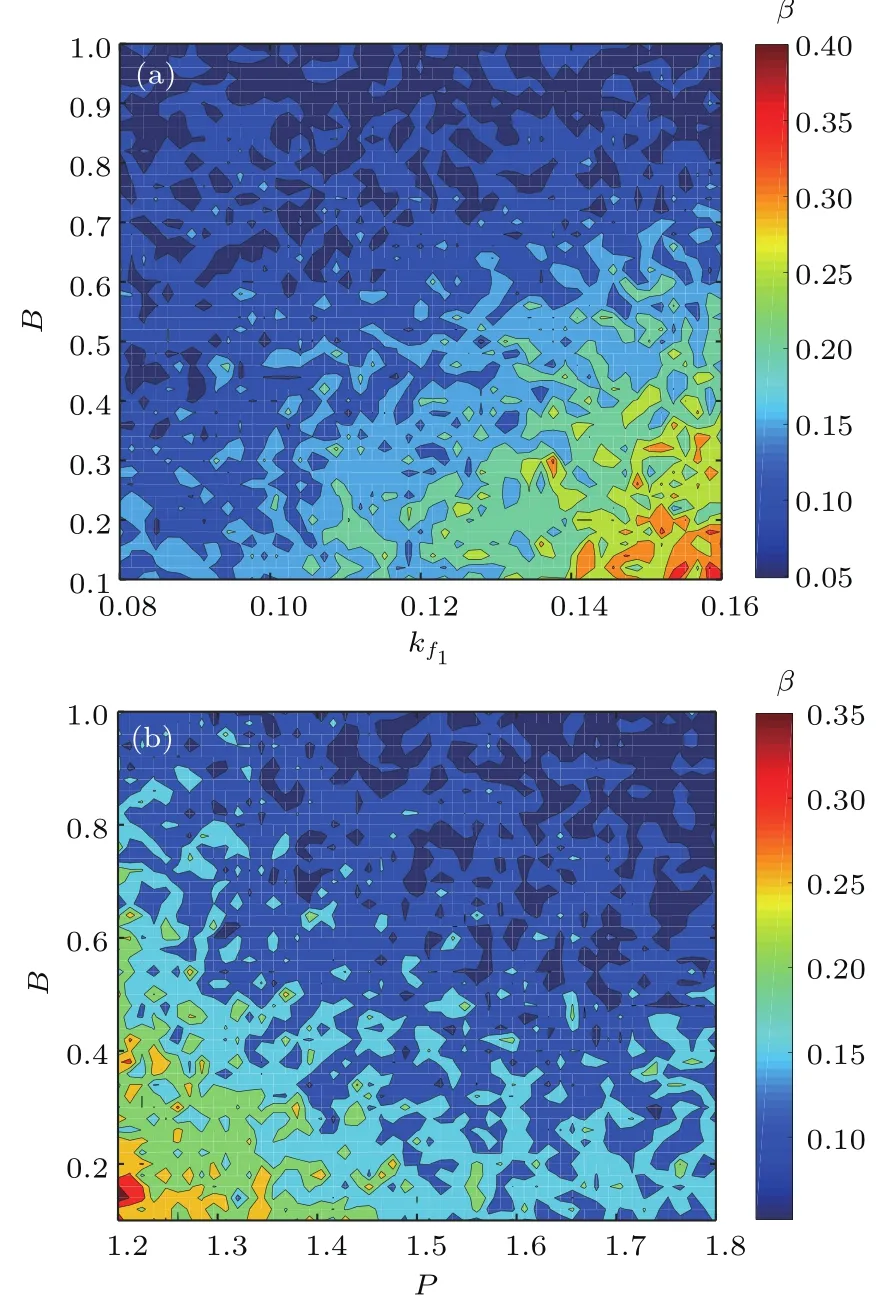
图4 (a)延时特征值β随参数B和kf1变化的二维图;(b)延时特征值β随参数B和P变化的二维图Fig.4.(a)Two dimensional maps of the time delay characteristic values β in the parameter space of B and kf1;(b)two dimensional maps of the time delay characteristic values β in the parameter space of B and P.

由图4(a)可见,对于确定的kf1,随着B的增大,整体趋势β是变小的,由图4(b)可见,对于确定的P,随着B的增大,整体趋势β也是变小的,即当B=1时,TDS被很好抑制,这是由于B=1时,相位调制器产生的相移φPMi(t)随着伪随机信号的变化灵敏,能较好地消除由于外腔反馈产生的弱周期性.对于图4(a),其左上角的大部分参数区间内,β值都小于0.2;但是当B<0.7时,随着kf1值的逐渐增大则反馈光增强,从而使由于反馈产生的弱周期性也随之增强,所以β值逐渐变大.对于图4(b),其右上角的大部分参数区间内,β值都小于0.2;但是当B<0.9时,随着P值在区间(1.2,1.6)内的增大,系统输出混沌激光的无序性增强[18],从而使外腔反馈产生的弱周期性减弱,所以β值逐渐变小;随着P值在区间(1.6,1.8)内的增大,系统输出混沌激光的无序性变化不明显[18],所以整体趋势是β值的减小趋于平缓.综上所述,在下面的数值计算中取B=1.

3.3 结果对比与分析

为了表明本文提出的方案(DFB-SL-DPMOF)能有效地抑制TDS,这里将DFB-SL-DPMOF和DFB-SL-DOF以及DFB-SL-SPMOF这3个系统对TDS的抑制效果进行对比和分析.首先对于DFB-SL-DOF(即双路光反馈),则(1)式中的φPM1=φPM2=0,这里取其他参数值和图2的对应相同,用这些参数值数值求解(1)—(2)式,得到τ1分别取2.08,2.48,2.88 ns时系统输出混沌激光的时间序列和对应的自相关函数曲线,如图5所示.

由图5(a1)—(a3)可见,激光强度的时间序列呈无规律的起伏状态,这说明此时系统输出的是混沌激光;由图5(b1)—(b3)都可以看到明显的尖峰,左边第一个尖峰几乎和纵轴重合,它是由弛豫振荡引起的[14],其右边的峰值依次出现在∆t为外腔延迟时间τ1和τ2整数(n)倍位置的尖峰是延时特征峰,并随着整数(n)的增加,延时特征峰的峰值逐渐下降,峰值最大的延时特征峰及其峰值(即延时特征值β)已经在图中标出.比较图5(b1)—(b3)可见:图5(b3)对TDS抑制的效果较好,但是在其中依然存在峰值约为0.1889的尖峰;比较图5(b3)和图2(b1)—(b3),前者对TDS的抑制程度不够理想,而后者(即DFB-SL-DPMOF)对TDS的抑制效果好.

然后对于DFB-SL-DOF,DFB-SL-SPMOF和DFB-SL-DPMOF这3个系统,分别以反馈系数kf1和抽运因子P作为控制参数.DFB-SL-DOF系统的参数取值和图5(b3)对应相同;对于DFB-SLSPMOF系统,则(1)式中的kf2=0,取B=1.0,其他参数取值和图2(b3)对应相同;DFB-SLDPMOF系统的参数取值:B=1.0,其他参数的取值和图4对应相同;数值求解(1)—(2)式,得到这3个系统输出混沌光的延时特征值β随kf1和P的变化趋势曲线,分别如图6(a)和图6(b)所示.

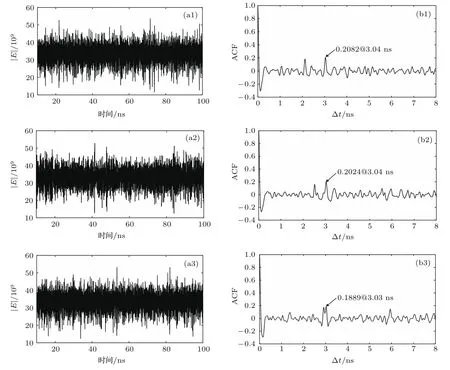
图5 DFB-SL-DOF在不同的延迟时间τ1下输出混沌光的时间序列(a1)—(a3)和对应的ACF曲线(b1)—(b3)(a1),(b1) τ1=2.08 ns;(a2),(b2) τ1=2.48 ns;(a3),(b3) τ1=2.88 nsFig.5.Time series(a1)–(a3)and the corresponding ACF curves(b1)–(b3)of chaotic laser from DFB-SL-DOF with Different delay time τ1:(a1),(b1) τ1=2.08 ns;(a2),(b2) τ1=2.48 ns;(a3),(b3) τ1=2.88 ns.

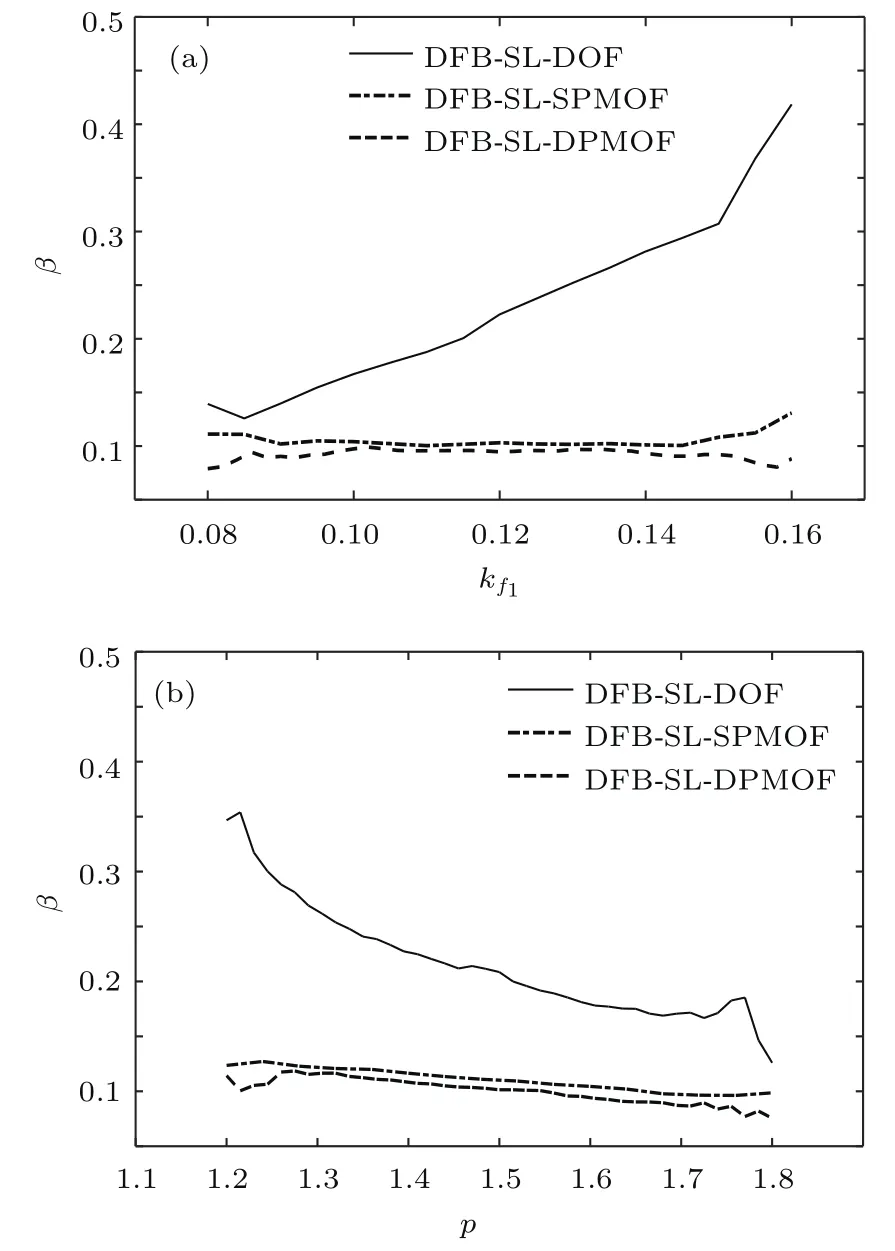
图6 对于DFB-SL-DOF,DFB-SL-SPMOF和DFB-SLDPMOF输出的混沌激光,延时特征值β随着kf1的变化(a)和延时特征值β随着P的变化(b)Fig.6.For chaotic laser from the DFB-SL-DOF,DFBSL-SPMOF,and DFB-SL-DPMOF,variation of the time delay characteristic values β with kf1(a)and variation of the time delay characteristic values β with P(b).

由图6(a)和图6(b)可见:在所选的控制参数值的区间内,DFB-SL-DPMOF系统输出混沌光的延时特征值β随着控制参数的变化整体较缓慢,曲线趋于平坦(这和图4相符),并且β值都在0.12以下,远小于DFB-SL-DOF系统输出混沌光的延时特征值β,同时也略小于DFB-SL-SPMOF系统输出混沌光的延时特征值β.其原因是:反馈腔中的相位调制器产生的相移能消除由于外腔反馈产生的TDS,所以图6(a)和图6(b)中DFB-SLSPMOF系统和DFB-SL-DPMOF系统输出混沌光的β值小于DFB-SL-DOF系统的β值;双路相位调制光反馈与单路相位调制光反馈比较,前者将使系统输出混沌光的混沌程度增强[22],所以图6(a)和图6(b)中DFB-SL–DPMOF系统输出混沌光的β值小于DFB-SL-SPMOF系统的β值.综上,比较而言DFB-SL-DPMOF系统对TDS的抑制效果最好.这证明本文提出的方案(即DFB-SL-DPMOF)对TDS抑制的有效性.

4 带宽的数值研究和分析

在DFB-SL-DPMOF中的TDS被较好地抑制的基础上,研究其输出混沌光的带宽.

4.1 抽运因子P对带宽的影响

分别取抽运因子P=1.2,1.4,其他参数值和图2(b3)相同,数值求解(1)式和(2)式,得到系统输出混沌光强度的时间序列和功率谱如图7所示.

对图7中的功率谱进行拟合,得到平滑后的功率谱曲线,见功率谱中白色曲线,经过分析得到图7(b1)和(b2)对应的3 dB带宽分别为2.8 GHz和3.7 GHz.由图7(a1)和(a2)可见激光器输出的是混沌激光,即在所选的参数条件下,改变抽运因子P则激光器输出混沌光的带宽随之变化.下面以抽运因子P作为控制参数,其他参数的取值和图7的对应相同,数值求解(1)式和(2)式,得到系统输出混沌光的3 dB带宽随抽运因子P的变化曲线如图8所示.

由图8可见,当抽运因子P在区间(1.1,1.6)内逐渐增大时,激光器输出混沌光的带宽整体呈线性增加趋势,带宽约增加2.0倍;当P大于1.6时,带宽的增长趋于平缓.其原因是,系统输出激光的混沌程度随着P在区间(1.1,1.6)内的增大而增强,从而使带宽随之增加;当P大于1.6时,继续增大P对系统输出激光的混沌程度影响不明显,则对带宽的影响不明显[18].

4.2 反馈系数kf1对带宽的影响

这里根据图8取抽运因子P=1.6,以反馈系数kf1作为控制参数,其他参数的取值和图7的相同,数值求解(1)式和(2)式,得到混沌光的3 dB带宽随kf1的变化曲线如图9所示.

由图9可见,当反馈系数kf1从0.08增加到0.16时,激光器输出混沌光的带宽整体呈递增的趋势,这里获得的混沌激光的带宽最大值约为7.2 GHz.这是因为在所选的参数范围内随着kf1的增加,一般来说会使系统输出混沌光的复杂度增加[22],从而拓宽了输出混沌光的带宽.可见在本文提出的方案中,通过适当选择参数的取值,可以使系统输出混沌光的带宽有所提高.

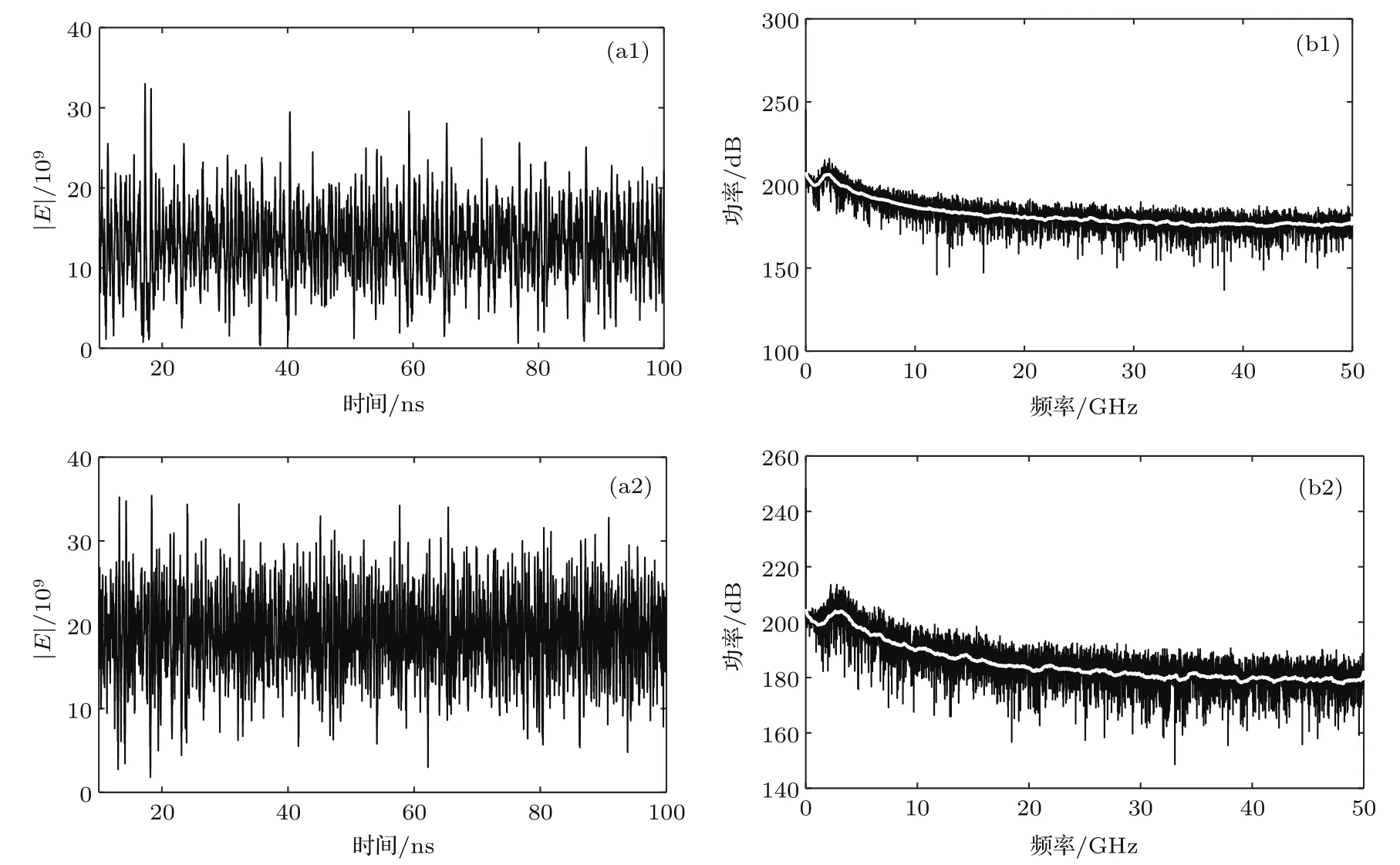
图7 不同抽运因子P下DFB-SL-DPMOF输出混沌光的时间序列(a1),(a2)及对应的功率谱(b1),(b2) (a1),(b1)P=1.2;(a2),(b2)P=1.4Fig.7.Time series(a1),(a2)and the corresponding power spectrums(b1),(b2)of chaotic laser from DFB-SL-DPMOF with Different pumping factors P:(a1),(b1)P=1.2;(a2),(b2)P=1.4.

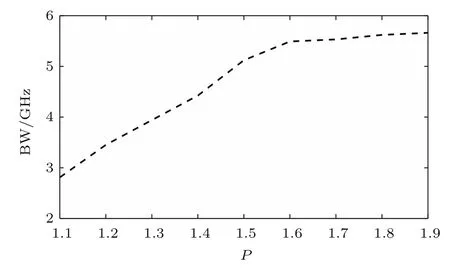
图8 DFB-SL-DPMOF输出混沌光的带宽随抽运因子P的变化Fig.8.Variation of the bandwidth with pumping factor P for chaotic laser from the DFB-SL-DPMOF.

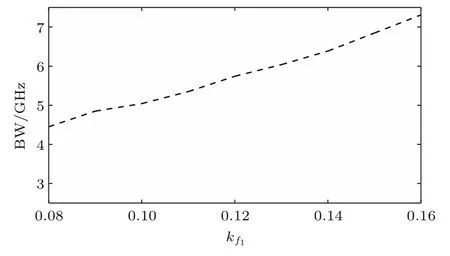
图9 DFB-SL-DPMOF输出混沌光的带宽随反馈系数kf1的变化Fig.9.Variation of the bandwidth with feedback coefficient kf1for chaotic laser from the DFB-SL-DPMOF.

5 结 论

采用双路相位调制光反馈的方案来抑制DFBSL输出混沌光的TDS并研究其带宽.首先数值研究了调制深度B、反馈系数kf1和抽运因子P对系统输出混沌光的TDS的影响,结果表明:在所选的参数条件下,DFB-SL-DPMOF系统(即本文所提方案对应的系统)输出混沌光的延时特征值β随着调制深度B的增加而变小,β随着反馈系数kf1的增加而变大,β随着抽运因子P的增加而变小.并且在所选参数范围的大部分区间内β<0.2,即实现了对TDS的较好抑制.进而通过对比发现,DFB-SL-DPMOF系统对TDS的抑制效果比DFB-SL-DOF系统和DFB-SL-SPMOF系统好.最后对于能较好地抑制输出混沌光TDS的DFB-SL-DPMOF系统和参数条件,数值研究了其输出混沌光的带宽随抽运因子P和反馈系数kf1的演化关系并进行了物理分析.数值结果表明:当抽运因子P从1.1增大到1.6时,激光器输出混沌光的带宽整体呈线性增长趋势,约增加2.0倍,当P大于1.6时,带宽的增长趋于平缓,这是由于抽运因子对系统输出激光的混沌程度的影响;随着反馈系数kf1的增加整体呈现递增的趋势,这是因为随着反馈系数的增加,一般来说会使系统输出混沌光的复杂度增加,从而拓宽了输出混沌光的带宽.这里获得的混沌激光的带宽最大值约为7.2 GHz.所以对于本文提出的方案,通过优化参数的取值,可以在较大的参数区间内抑制混沌光的TDS并使其带宽有所提高.从而证明了本文所提出方案的有效性.本文的结果对于混沌激光的应用是有意义的.