基于部分测量增强量子隐形传态过程的量子Fisher信息∗

武莹 李锦芳 刘金明

(华东师范大学,精密光谱科学与技术国家重点实验室,上海 200062)

(2018年2月13日收到;2018年4月3日收到修改稿)

量子Fisher信息(QFI)是量子度量学中的一个重要物理量,可给出预估参数精度的最优值.本文研究如何引入弱测量和测量反转操作,来提高有限温环境下以Greenberger-Horne-Zeilinger态作为量子通道的隐形传态过程中的QFI.依据隐形传态过程中量子比特的传输情形,考虑了三种不同方案相应的QFI.首先,通过构造每种量子隐形传态方案的量子线路图,分析了QFI与推广振幅衰减噪声参数的变化关系.随后对各种方案中的受噪声粒子施加弱测量和测量反转操作,并对相应的部分测量参数进行优化,着重探讨了施加最优部分测量操作后QFI的改进量.结果表明,经过优化后的部分测量操作能有效提高有限温环境下量子隐形传态过程输出态的QFI;而且量子系统所处的环境温度越低,QFI的提高效果可越显著.

1 引 言

量子通信作为量子力学和信息学相结合的新兴研究领域,是指基于量子纠缠特性进行信息传递的一种通讯方式.近年来,国内外关于量子通信的研究发展迅速,相关成果和新技术不断涌现.2016年,世界上首颗量子卫星“墨子号”成功发射,标志着我国的量子通信技术达到国际领先水平[1,2].量子隐形传态是量子通信领域的一个重要分支,其原创性思想由Bennett等[3]在1993年首次提出.此后,关于量子隐形传态的研究及其应用受到人们的极大关注[4,5],陆续拓展了多种推广的量子隐形传态方案,如连续变量隐形传态[6−9]、量子秘密分享[10−12]、可控隐形传态[13−17]、概率隐形传态[18−21]、双向隐形传态[22,23]等.1997年,奥地利的Zeilinger小组[24]首先在线性光学系统中实验实现了单光子态的隐形传送;2017年，国内潘建伟团队[25]首次实现了从地面到卫星千公里级的量子隐形传态.

量子隐形传态过程中,量子系统不可避免地将与周围环境发生相互作用,使系统的相干性遭受损失,导致被传递信息的失真.保真度是表征量子隐形传态的一个重要物理量,它描述输入态和输出态之间的偏差程度.在度量学中,量子Fisher信息(QFI)同样占据着不容忽视的地位[26,27],它是在经典Fisher信息基础上的推广,可量化预估计参数所携带的信息量[28].研究表明,QFI极易受到环境噪声的影响,导致测量精度的下降,因此提高QFI尤为重要.20世纪80年代,Aharonov等[29]提出了弱测量的概念,弱测量及其反转操作又被称为部分测量[30,31].相对于传统的von Neumann测量,弱测量对量子系统有较小的扰动,且施加弱测量之后加入适当反转操作可使量子态以一定的概率恢复至其初始态,起到保护量子态的作用.因此,弱测量方法被广泛应用于一些量子信息任务[32−34],如保护开放系统的退相干[35−39]、增强量子关联[40,41]和提高传输量子态的保真度[42]等.实验上,人们已在线性光学系统[43,44]和超导体系[45,46]中成功地实现了弱测量.

Pramanik和Majumdar[47]以及Qiu等[48]利用弱测量方法分别提出了改进零温振幅衰减噪声下量子隐形传态过程保真度的方案.Xiao等[49]研究了零温环境下弱测量对基于EPR态的量子隐形传态过程中QFI的影响,并分析了如何采用部分测量操作来提高量子隐形传态过程中的QFI.实际上,零温环境仅是一种理想情况,真实量子系统无法达到零温情形,因此温度的影响通常是不能忽略的[38].鉴于此,本文研究有限温环境下部分测量操作对以Greenberger-Horne-Zeilinger(GHZ)态作为纠缠通道隐形传送单比特态过程中的QFI的影响,并通过优化部分测量操作来改善推广振幅衰减噪声下输出态的QFI.结果表明,合适的部分测量操作可显著增加非零温环境下的QFI;且环境温度越低,增加效果越好.

2 基本概念

2.1 有限温环境下的振幅衰减通道

零温环境下,描述单量子比特S和二能级环境E的振幅衰减(AD)噪声具有如下的变换关系[50]:

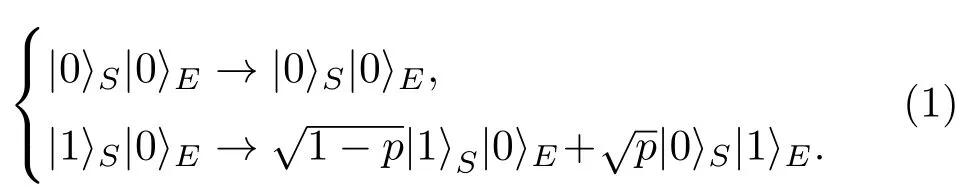
其中

然而,零温环境只是理想情况,真实物理系统不可能达到.有限温环境下,单量子比特不仅能通过自发辐射从激发态跃迁到基态,同时也可以从环境中吸收能量由基态跳变到激发态.有限温情形下,单量子比特态经历推广的振幅衰减(GAD)噪声[38]可表示为

其中

2.2 弱测量和弱测量反转操作

弱测量操作可使量子比特的初态以一定的概率跃迁到基态,而弱测量反转操作则可使量子比特的末态以某种概率恢复至初态.因此,某种程度上实施弱测量和测量反转操作可以起到抑制量子纠缠态的退相干和保护量子态的作用.本文采取以下作用于量子比特l(l=1,2,3)的弱测量算符[42,43]:

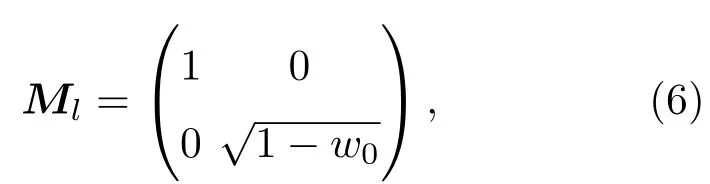
相应的作用于量子比特l的弱测量反转算符可表示为

其中参数w0,w1分别表示弱测量操作和弱测量反转操作的强度,w0,w1的取值范围均为[0,1].

2.3 量子Fisher信息

在物理学中,人们非常关心测量的精度问题.QFI提供了一种估计参数测量精度的有效方法.众所周知,基于布洛赫球表示,任意单量子比特态可写为

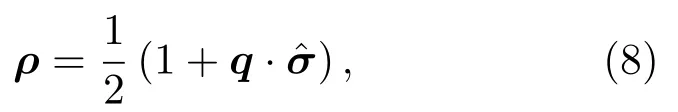
其中q=(qx,qy,qz)T表示布洛赫矢量,=表示Pauli矩阵.对于单量子比特态,编码在该态的参数ϕ的QFI可表示为[27,49]

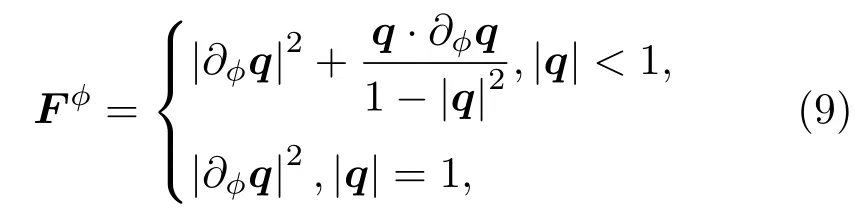
其中∂ϕ表示对矢量q中的参数ϕ求偏导.

3 GAD噪声环境下引入弱测量方法的量子隐形传态过程

本节描述噪声情形下基于GHZ态作为纠缠资源的量子隐形传态协议.假定初始GHZ纠缠态的形式为

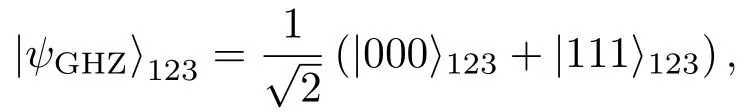
待传输的单量子比特态为

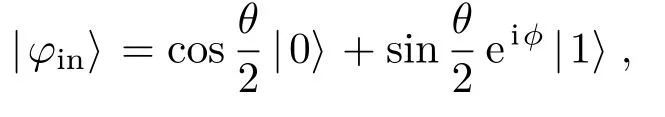
这里θ,ϕ是与输入态有关的参数.下面考虑三种GAD噪声情况下量子隐形传态过程中的QFI.

3.1 单粒子通过GAD噪声

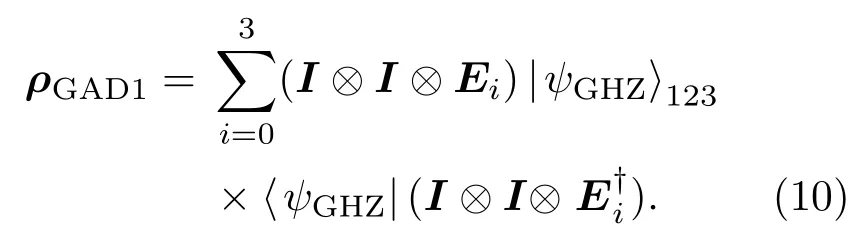
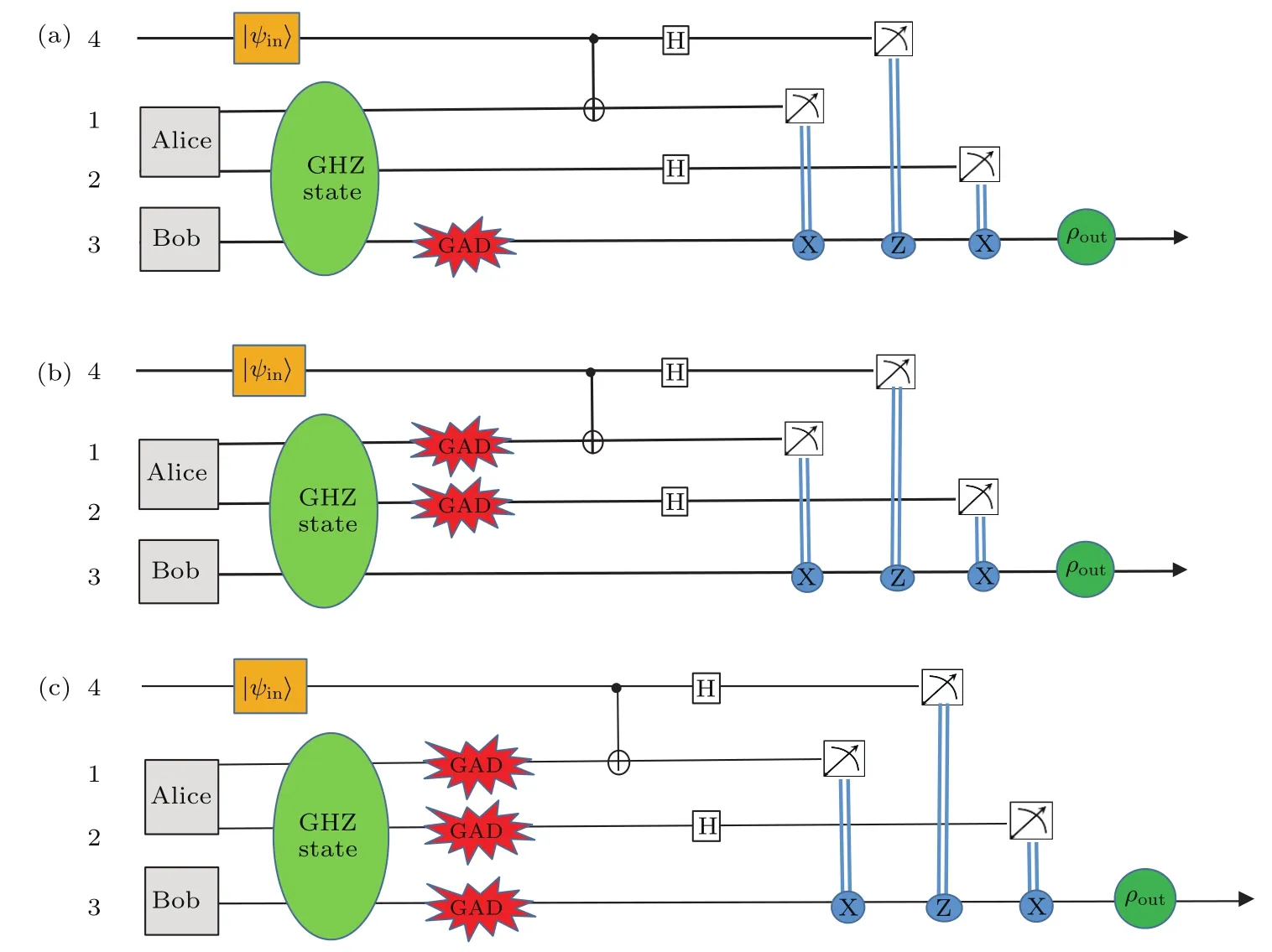
图1 基于GHZ态隐形传送单比特态的量子线路图 (a)粒子3遭受GAD噪声;(b)粒子1和2遭受GAD噪声;(c)粒子1,2和3同时遭受GAD噪声Fig.1.A quantum circuit for teleportation of a single-qubit state via a GHZ state:(a)Only qubit 3 undergoes decoherence;(b)qubits 1 and 2 undergo decoherence;(c)qubits 1,2 and 3 simultaneously undergo decoherence.

根据量子线路图1(a),量子隐形传态过程的输出态可写为

其中,幺正操作

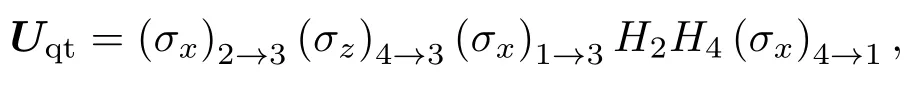
这里(σλ)n→m表示两比特控制旋转操作;n为控制比特;m为目标比特;λ=x,z;n=1,2,4;m=1,3;H2和H4分别表示对粒子2和4实施Hadamard操作.

经过解析计算,输出态的密度矩阵可表示为

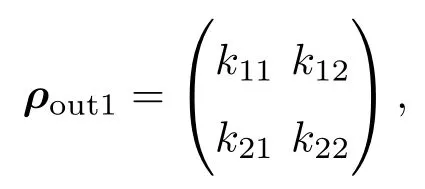
其中

由(9)式可导出输出态ρout1的QFI为

令θ=π/2,由(12)式可知,p一定的情况下,r增大,也增大.

为考虑部分测量操作对QFI的影响,在粒子3发送前和经过噪声通道后,分别由Alice和Bob对粒子3执行弱测量和弱测量反转操作,见图2.这样在粒子3经历GAD噪声,并被实施前置弱测量和后置测量反转操作后,量子隐形传送的输出态可表示为

其中

依据(9)式和(13)式,执行部分测量操作后输出态的QFI可写为

其中

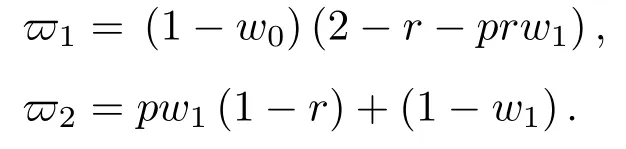
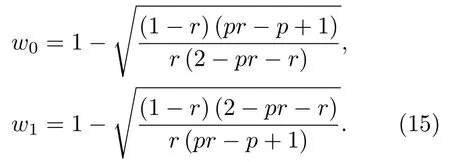
根据(15)式,因为w1的取值为[0,1],可知相应参数r的有效取值应为

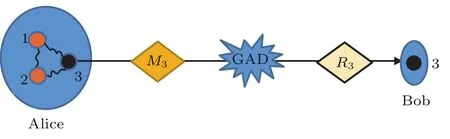
图2 对粒子3实施前置弱测量和后置测量反转操作Fig.2.Performing a weak measurement and a measurement reversal on particle 3.

将(15)式中的w0和w1代入(14)式,可得到输出态的QFI的最优值对于给定的参数p和r,现定义对粒子3引入部分测量操作后相应的QFI最优值与未引入部分测量操作的QFI值之差为

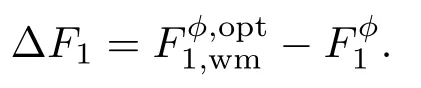
图3给出了QFI的改进量∆F1随参数r和θ以及参数r和p的变化.从图中可知,量子隐形传送输出态的QFI改进量∆F1总是非负的.图3(a)表明,对于给定的r值,∆F1随θ的增加而增大,当θ=π/2时,QFI的改进量最多.从图3(b)可看出,在r和p取不同的值时,最佳弱测量和测量反转操作对QFI的改善效果不尽相同;对于给定的较大p值,∆F1随着r的变大而增大,在r接近1时显著增加.

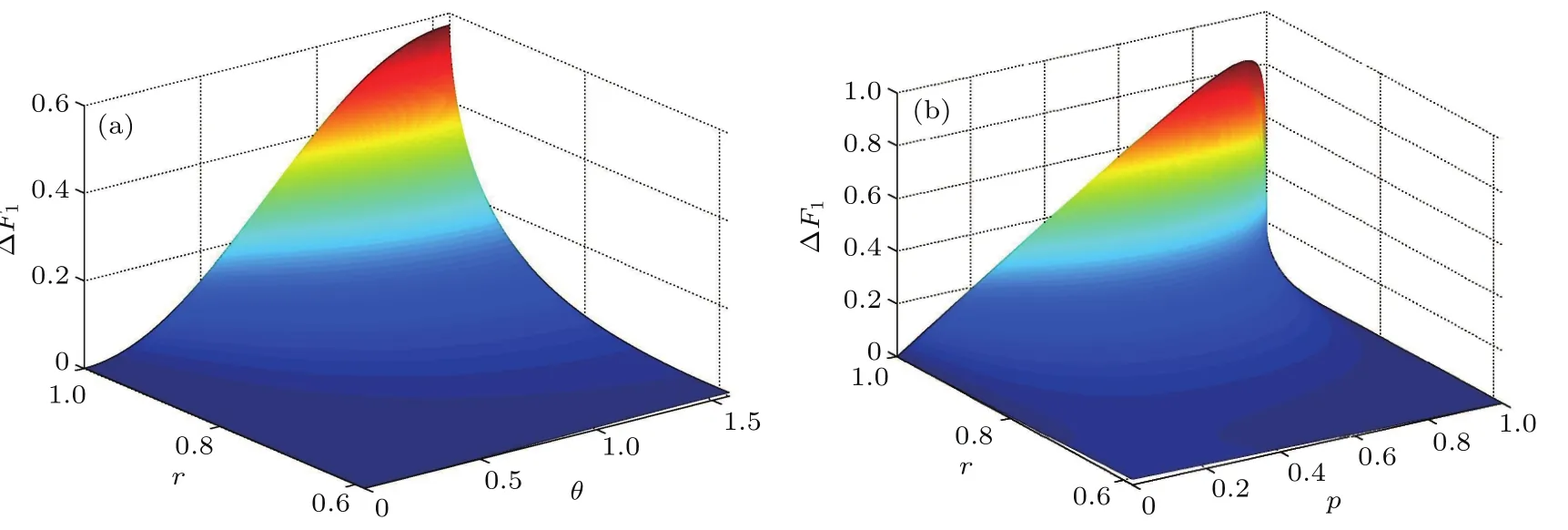
图3 (a)当p=0.6时,QFI的改进量∆F1随参数r和θ的变化;(b)当θ=π/2时,QFI的改进量∆F1随参数r和p的变化Fig.3.(a)The improved QFI ∆F1by optimal partial measurements is plotted as a function of r and θ for p=0.6;(b)the improved QFI∆F1by optimal partial measurements is plotted as a function of r and p for θ= π/2.

图4给出了∆F1随噪声参数p的变化情况.从图4可知,当r值给定时,∆F1随p的增大先增加而后减小;r越大,∆F1的峰值越高,峰值处对应的p值也越大.物理上可以理解为:对于给定的r值,p较小时,GAD噪声对QFI的影响较弱,输出态QFI的信息损失较小,部分测量操作的优化对提高QFI的效果微弱;随着噪声参数p的逐渐增大,输出态QFI的信息损失变大,此时部分测量凸显出对QFI的保护作用,且p值越大效果越明显;当p增大到一定值时,部分测量对QFI的改进作用达到极值;随着参数p的继续增大,作为量子通道的纠缠资源逐渐趋于经典态,则用于抑制量子态消相干的弱测量操作效果逐渐退化,因而导致QFI的改进幅度减小.在非零温环境下,输出态的QFI改进量依赖于参数p和r.注意到参数r是温度T的反关联函数,即在低温环境下,选取合适的p值,部分测量操作可显著提高输出态的QFI,这有助于实现量子计量和相关量子信息任务.

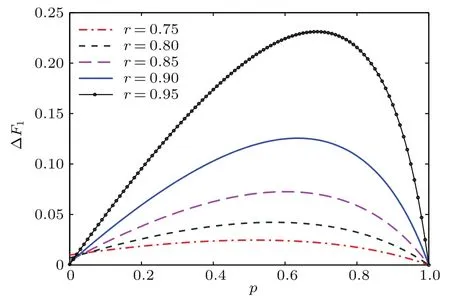
图4 当θ=π/2时,对于不同的r值,QFI的改进量∆F1随参数p的变化Fig.4.The improved QFI∆F1by optimal partial measurements is plotted as a function of p with Different values of parameters r for θ= π/2.

3.2 两个粒子通过GAD噪声

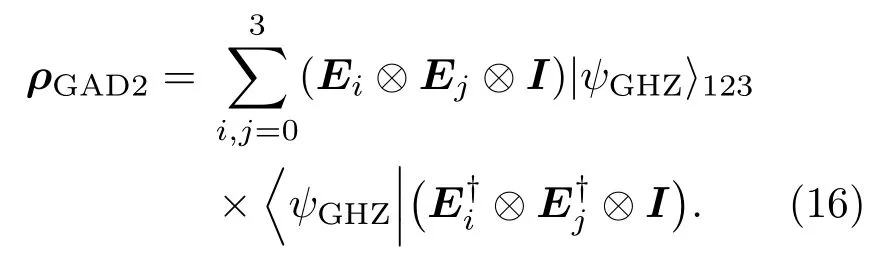
为简便起见,假设粒子1,2受到相同噪声的影响,即r1=r2=r,p1=p2=p.类似地,基于(11)式,最终输出态的密度矩阵可表示为

其中

由(9)式可导出输出态ρout2的QFI为

为考虑部分测量操作对QFI的影响,在粒子1和2发送前和各自经过噪声通道后,分别由Bob和Alice对两粒子执行弱测量和弱测量反转操作,见图5.在粒子1和2经历GAD噪声,并被实施前置弱测量和后置测量反转操作后,量子隐形传送的输出态可表示为

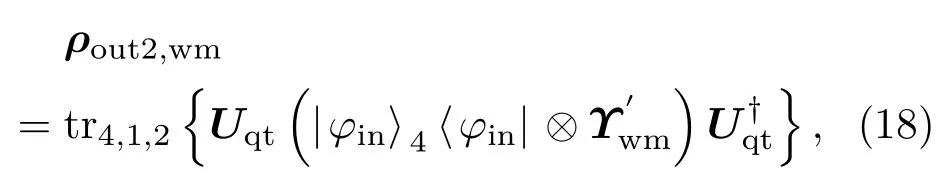
其中

依据(9)式和(18)式,此时输出态的QFI可导出为

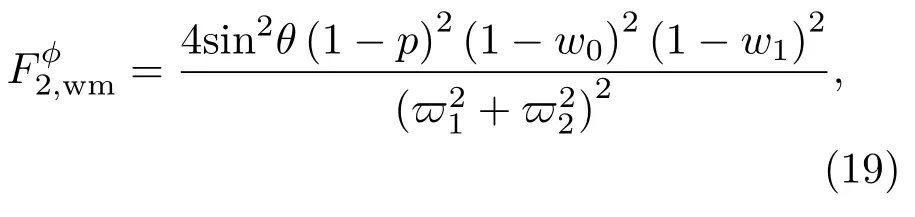
数学分析表明,当弱测量参数w0=和弱测量反转参数w=1−1可获得输出态的的最优值为

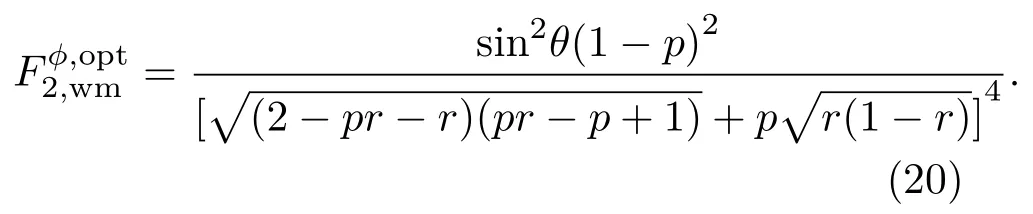
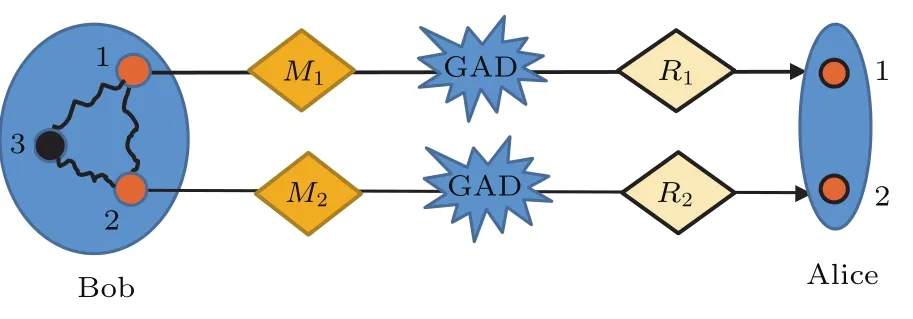
图5 粒子1,2传输过程中实施前置弱测量和后置测量反转操作Fig.5.Performing prior weak measurements and subsequent measurement reversals on particles 1 and 2 during the two qubit transmission processes.

因为w1的取值为[0,1],可知相应参数r的有效取值也应为

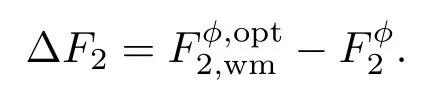
图6给出了当θ=π/2时,∆F2随GAD噪声参数r和p的变化.从图6(a)中可知,量子隐形传送输出态的QFI改进量∆F2总是非负的,即经实施最优弱测量和测量反转操作后输出态的QFI较之无部分测量情形下的QFI都有提高.从图6(b)可发现,当r值较大时,∆F2随p的增大先逐渐增加而后慢慢减小;r越大对应的∆F2的峰值也越高.因此,从图6所得到的结果与图3和图4所得的结果类似.换句话说,在量子系统所处的环境温度较低时,选取合适的p值,优化部分测量操作可显著地提高传送初始态的QFI,有效抑制输出态QFI的信息损失,这对于相关量子通信和量子计量研究非常重要.

图6 (a)当θ=π/2时,QFI的改进量∆F2随参数r和p的变化;(b)图(a)在给定参数r时的二维图Fig.6.(a)The improved QFI∆F2by optimal partial measurements is plotted as a function of r and p for θ= π/2;(b)the two-dimensional figure of panel(a)for the given r.

3.3 三个粒子通过GAD噪声

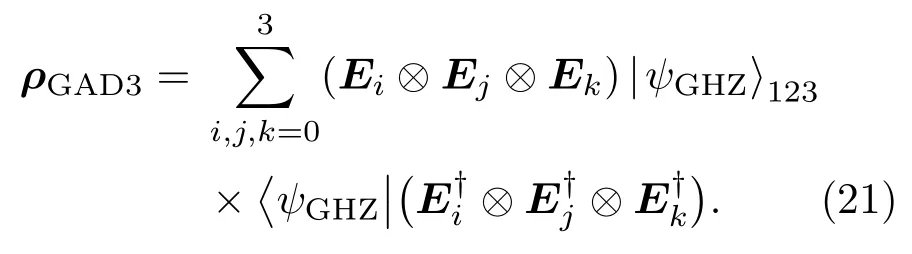
简单起见,假定三粒子受到相同的GAD噪声影响,即r1=r2=r3=r,p1=p2=p3=p.

根据(11)式，并采用前两个小节类似的方法,量子隐形传送输出态的QFI表达式可写为

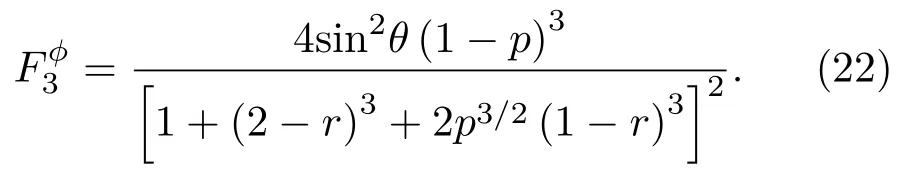
现考虑部分测量操作对QFI的影响,在三个粒子发送前假设由Charlie对它们分别实施前置的弱测量操作,各自经过独立的GAD噪声后,分别被实施后置的弱测量反转操作,如图7所示.不失一般性,假定M1=M2=M3且R1=R2=R3.类似于前两小节的方法,执行部分测量操作后隐形传送的输出态可表示为

其中

根据(23)式,在给定参数θ,r p的情形下,数值分析表明,通过选取合适的部分测量参数w0和w1可使得达到最优值定义QFI的改进值∆F3=−令θ=π/2,∆F3随参数r和p的变化见图8(b).从图中可知,量子隐形传送输出态的QFI改进量∆F3也总是非负的,换句话说,优化部分测量操作也可提高量子隐形传送过程中三个粒子同时经历GAD噪声后输出态的QFI,且改进效果显著.

图8 当θ=π/2时,QFI(a)和QFI的改进量∆F3(b)随参数r和p的变化Fig.8.QFI(a)and the improved QFI∆F3(b)is plotted versus p and r for θ=π/2.

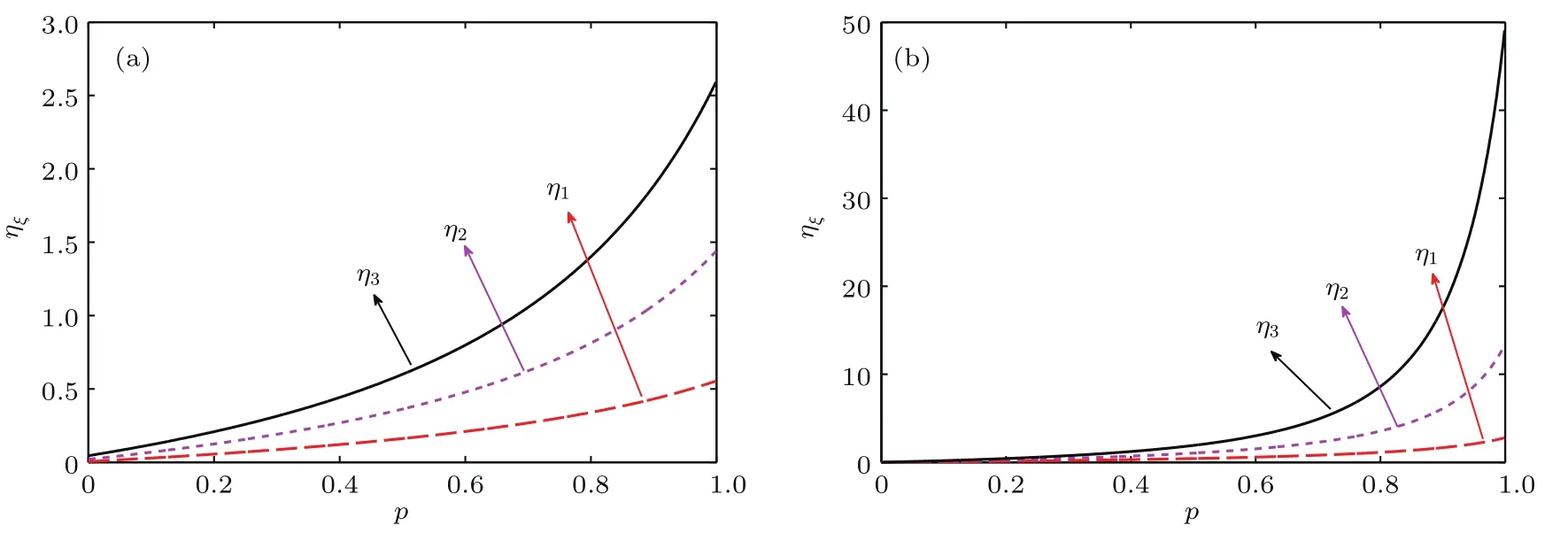
图9 优化部分测量操作对三种传输方案遭受GAD噪声影响下QFI的改进效率ηξ随参数p的变化 (a)r=0.85;(b)r=0.95Fig.9.The improvement efficiency ηξ of QFI is plotted versus the parameter p for three kinds of teleportation schemes suffering from GAD noises after the optimization of partial measurements:(a)r=0.85;(b)r=0.95.

通过以上分析量子隐形传态过程中粒子遭受GAD噪声以及实施部分测量操作的三种情况,可以发现:尽管三种传输方案不尽相同,但优化部分测量操作后的QFI的改进量总是非负的,也即弱测量操作可起到保护量子态,提高QFI的作用;而且量子系统的环境温度越低,部分测量操作对提高QFI越有效.为了对比三种传输方案受到噪声的影响,图9给出了优化部分测量操作对量子隐形传送输出态QFI的改进效率ηξ随参数p的变化,这里定义

从图9可知,在r值取定时,改进效率ηξ随参数p的变大而增加,且数值分析表明总存在η3>η2>η1.换言之,部分测量操作的优化对QFI的改进效率与遭受GAD噪声的粒子数有关;受噪声的粒子数越多,所需实施的部分测量优化操作也相应地增加,QFI的改进效率随之提高.

4 结 论

本文研究了采用部分测量方法改进推广振幅衰减噪声下以GHZ态作为量子信道的单比特态隐形传送过程的量子Fisher信息.考虑了三种粒子遭受噪声的情形,分析了部分测量的引入对各种情形的影响,并解析导出了三种情形下的QFI以及单个和两个粒子受GAD噪声下优化后的QFI.对于三个粒子同时经历GAD噪声的情况,鉴于解析式复杂,通过数值分析得到了相应的最优QFI.研究表明,在噪声参数p增大或r减小时,GAD噪声影响下三种输出态对应的Fisher信息(即和)都减小.对于单粒子和两粒子经历GAD噪声的情形,最优的弱测量参数w0和测量反转参数w1都是p和r的函数;而且三种粒子受噪声的情形下QFI的改进量∆F1,∆F2和∆F3总是非负的,这隐含着经引入最优弱测量和弱测量反转操作后输出态的QFI较之未引入情形下的QFI都有所提高.此外,受GAD噪声的粒子数越多,优化部分测量操作对QFI的改进效率越高.进一步分析表明,在低温环境下,选取合适的p值,部分测量操作可显著提高GAD噪声影响下输出态的QFI,这有利于相关量子参数估计和量子信息任务的实现.本文结果可加深对部分测量技术应用于量子隐形传态方案的理解,也对研究如何抑制量子通信过程中QFI信息的退相干具有一定的启发和参考意义.