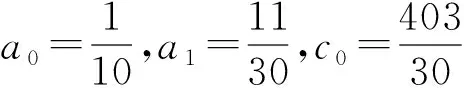一类2n阶常微分方程的奇周期解
2018-10-29李永祥
李永祥,文 乾
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
奇2π-周期解的存在性,其中n是正整数,f:R×RnR连续且关于t是以2π为周期的奇函数.运用Leray-Schauder不动点定理与Fourier分析方法,在允许非线性项f超线性增长的条件下,获得了该方程的奇2π-周期解.
1 引言及主要结果
文中讨论2n阶常微分方程

常微分方程周期边值问题是现代数学的一个重要分支,周期现象的普遍存在使得这一问题的研究具有重大的理论价值和实际意义.近年来,高阶常微分方程周期解存在性的研究越来越受到人们的重视[1-9].这些文献采用的方法主要有上下解的单调迭代方法与拓扑度相关的不动点方法.但对于奇周期解的存在性,迄今为止研究较少.
对于二阶常微分方程
u″(t)=f(t,u(t)),t∈R
(2)
奇周期解的存在性已有研究[10-12].文献[12]在非线性项f超线性或次线性增长条件下,运用锥上的不动点指数理论,首先获得了t∈[0,1]时正周期解的存在性;经逐次延拓,最终获得了方程(2)奇的振荡2π-周期解的存在性结果.
文献[9]在非线性项满足如下增长性条件:
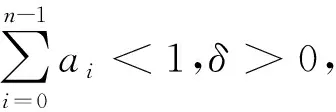
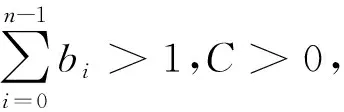
在一次增长条件下,分别运用锥上的不动点指数理论与Schauder不动点定理获得了方程(1)奇2π-周期解的存在性及唯一性.但对于方程(1)允许非线性项f单边超线性增长的情形并未讨论.文中在允许非线性项f单边超线性增长的条件下,运用Leray-Schauder不动点定理与Fourier分析方法,获得了方程(1)奇2π-周期解的存在性结果.主要结论如下:

(F1)f为奇函数,即
(F2)存在常数a0,a1,a2,…,an-1≥0满足a0+a1+a2+…+an-1<1及c0>0,使得f满足
则方程(1)至少存在一个奇2π-周期解.
注1:在定理1中,条件(F2)允许f(t,x0,…,xn-1)关于x0,x1,…,xn-1超线性增长,见例1.
2 主要结果的证明
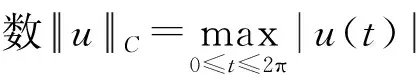
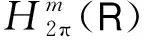
设h∈H,首先考虑2n阶线性常微分方程
u(2n)(t)=h(t),t∈R
(3)
2π-周期解的存在性.

证明∀h∈V可表示为Fourier正弦级数:
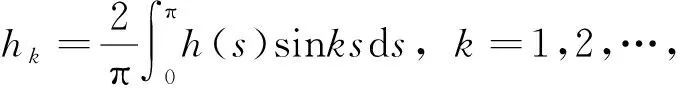
成立.容易验证
(4)

引理2对∀h∈V,方程(1)的奇2π-周期解u∈V2n满足
||u(2k)||2≤||u(2n-1)||2,k=0,1,…,n-1.
证明设u∈V2n为方程(1)的奇2π-周期解,则u,u″,…,u(2n-2)为奇函数,可展为正弦级数,u(2n-1)为偶函数,可展为余弦级数.设u的展式为
党的十七届六中全会提出了大力推进社会主义文明建设,水文化是文化建设和社会主义精神文化建设的重要内容。堤防工程置于自然,融于自然,堤防绿化使蜿蜒堤段成为亮丽的风景。在人流密集堤段,建设几处醒目的水文化亮点,可以作为洙赵新河的闪亮名片,同时满足了群众日益增长的物质文化需求。
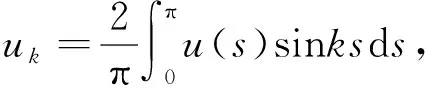
由Paseval不等式,有
因此,
||u(2m)||2≤||u(2n-1)||2,m=0,1,…,n-1. 】
从引理2的证明可知||u(2n-1)||2为||u||2n-1,2的等价范数.为了论述的方便,用X代表空间V2n-1中赋以范数||u||X=||u(2n-1)||2构成的Banach空间.
定理1的证明对∀u∈W2n-2,令
F(u)(t)=f(t,u(t),u″(t),…,u(2n-2)(t)).

考虑同伦方程簇
u=λAu,0<λ<1.
(5)
需要证明方程簇(5)的解集在W2n-2中有界.设u∈W2n-2为方程簇(5)中λ∈(0,1)对应的解,则u=S(λF(u)).
令h=λF(u),则由S的定义可知,u=Sh为线性方程(3)的唯一奇2π-周期解,因此u∈W2n满足方程
u(2n)(t)=λf(t,u(t),u″(t),…,u(2n-2)(t)).
上式两边同乘以-u(2n-2)(t)然后在[0,2π]上积分,由条件(F2)与引理 2,有
所以


则周期边值问题(1)存在奇2π周期解.
若记
则有如下推论:

例1考虑超线性增长的四阶常微分方程
容易验证相应的非线性项
(7)
满足条件(F1).对∀(t,x0,x1)∈R3,由(7)式可得
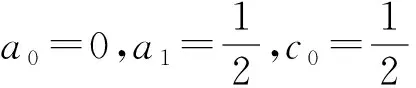
例2考虑次线性增长的四阶常微分方程

(8)
易知,相应的非线性项
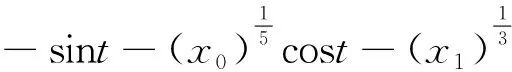
(9)
满足条件(F1).
下证f满足条件(F2).对∀(t,x0,x1)∈R3,利用Young不等式:
结合(9)式可得
所以