基于Zanker型流动调整器的平面双弯头流场特性研究
2018-10-29张巧玲曹佳豪杨振东李国栋
张巧玲,曹佳豪,杨振东,李国栋,薛 文
(西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西西安710048)
农田水利的大力兴建是我国农业发展的重要举措,而农业灌溉系统中流量的准确测量至关重要,实际生产中常采用流量传感器来获得精确的流量。要想使流量测量仪器的精度达到所需的要求,在实际生产应用中,一般采用在流量测量仪器前面加设20~30倍的直管道,来降低或消除上游造成的不稳定流动状态。平面双弯头广泛运用于连接高差突变的管路中,而平面双弯头下游流体的流动和充分发育的紊流流动状态相差甚远,因此,可在管道上加装流动调整器,用以消除不正常流动,同时,缩短必要的直管段长度,可以在较短的直管段条件下形成稳定无漩涡的充分发展流动状态。所以,研究流动调整器对平面双弯头产生的畸变流场的调节作用具有非常重要的意义。
流动调整器是加速不规则流场稳定、消除漩涡等非正常流动对流体影响的重要仪器,在流体能源计量与监控、流量监测系统、流量传感器等领域得到广泛应用[1]。常见的流动调整器包括管束式、栅格式、孔板式等[2],Zanker型流动调整器在各领域内都得到了广泛应用。很多学者通过实验对扰流件及流动调整器对管内流场的具体影响做了一定的研究,但由于实验系统复杂、成本高,现在大部分采用数值模拟的方法对流场进行分析,因其用时短且更快捷。Mattingly和Yeh[3]研究了90°单弯头对孔板流量计流出系数的影响,认为90°单弯头会产生漩涡流,并使孔板流量计的测量值低于实际值,在较小节流比时误差约为2%,在较大节流比时误差约为6%。Laws[4]研究认为旋流衰减十分缓慢,对由不同平面90°双弯头形成的旋流,要达到节流装置流量测量标准(ISO 5167)提出的小于2°的旋流角的要求,需要超过100倍管径的直管段长度。Laribi等[5]分别研究了平面双弯头和不同平面双弯头条件下旋流对标准孔板流量计测量精度的影响,研究表明旋流会导致2%~4%的误差。Shen[6]提出了一种可以很好地形成不同平面90°双弯头旋流的装置,分析了旋流对标准孔板流量计流量系数的影响,结果表明旋流最大会造成5%的测量误差。Brennan等[7]也研究了不同的旋流条件下压差式流量计流出系数Cd与理论值的偏差,结果表明Cd的最大偏差为5%。Morrison等[8]研究了旋流条件下孔径比对孔板流量计测量精度的影响,结果发现取大孔径比β=0.75时,流出系数Cd最大偏差25%,而取小孔径比β=0.50时,Cd最大偏差5%。Ahmadi[9]研究了平面双弯头形成的旋流对标准孔板型流量计测量精度的影响,结果表明两种旋流条件下流出系数最大偏差4%左右;同时,还提出了一种锥形旋流调整器,该调整器能够消除不对称速度分布,但无法消除旋流。万勇等[10]提出了一种基于计算流体动力学(Computational Fluid Dynamics,CFD)仿真技术的流动调整器性能评价方法,对流动调整器的设计和提高流量测量仪器精度有很高的参考价值。谭文胜[11]、陈国宇[12]、姚贤卿[13]、张涛[14]等在对各种管道所适应的流动调整器进行设计优化的基础上,发明了新型流动调整器。李杰等[15]采用数值模拟和实验测试相结合的方式,研究了弯管后内部流动的非均匀分布特性,并采用整流装置改善了弯管后的非均匀流场。王慧锋等[16]通过实验研究了不同管径及等效直径比下A+K平衡流量计在上游安装同平面90°双弯头时所需的最短直管段长度。屈鑫鑫[17]采用PIV(Particle Image Velocimetry)测试技术,实验研究了经过不同平面双弯管时的流场分布情况,并分析了四类不同流动调整器的整流效果。
综上所述,国内外学者对流动调整器的研究成果较多,但对于平面双弯头后Zanker流动调整器的研究还不够完善。故本文对带有Zanker型流动调整器(平面图如图1所示)的平面双弯头流场特性进行了精细数值模拟,通过分析整流效果,揭示其内部流动机理。该研究成果可为提高流量测量设备的准确性提供理论依据。
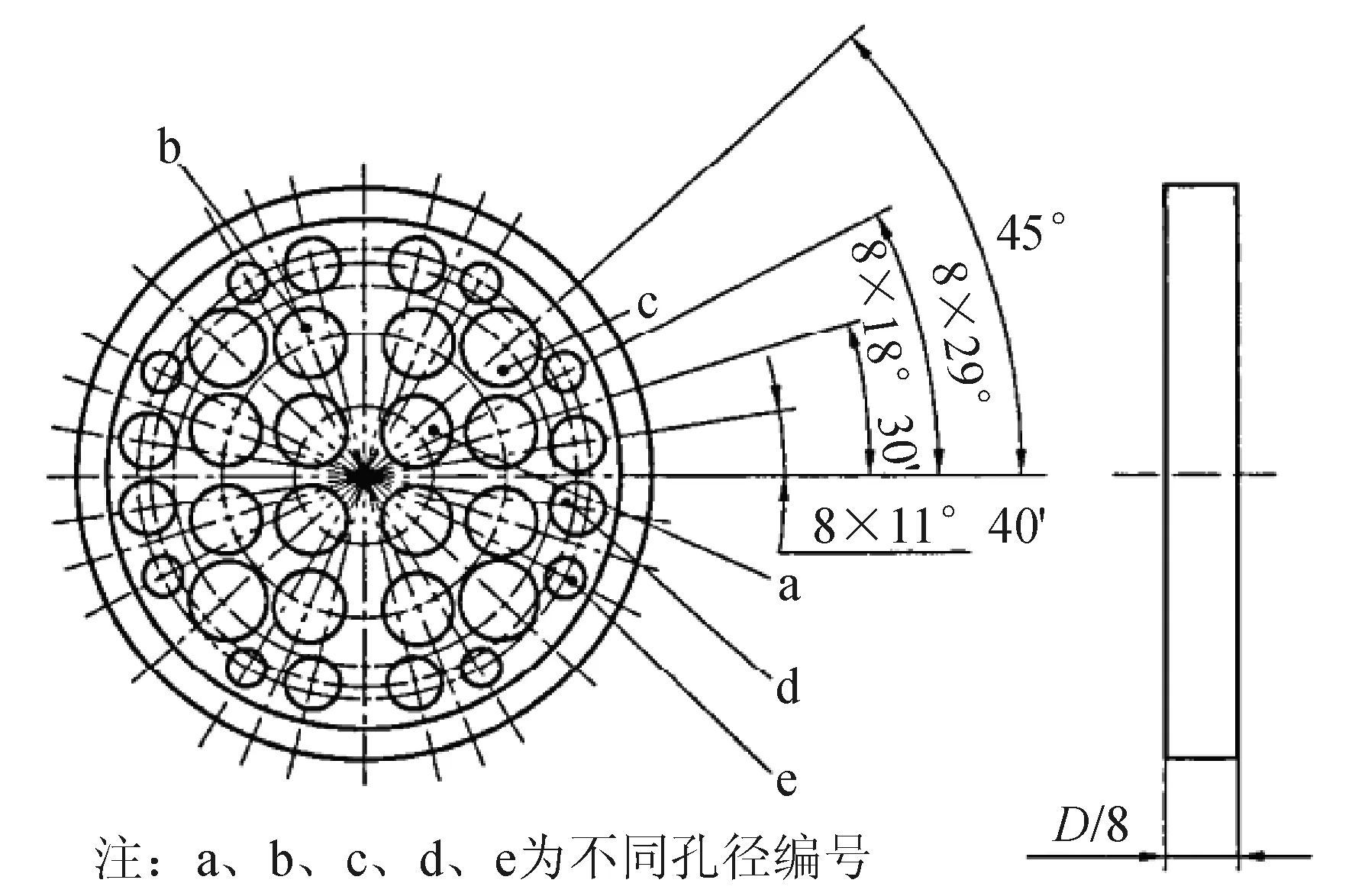
图1 Zanker型流动调整器平面图Fig.1 Floor plan of Zanker-type flow regulator
1 数学模型
1.1 控制方程
水流的控制方程为连续方程和动量方程:
(1)
(2)

1.2 湍流模型
本文基于RNGk-ε湍流数学模型对平面双弯管内的流场进行数值模拟。RNGk-ε湍流模型是目前应用最广泛的双方程模型,实践表明,结合标准壁面函数法进行近壁面处理,RNGk-ε模型可以非常好地预测管道内的流动,其数学模型为:
(3)
(4)
式中,k为湍动能;μ为动力黏滞系数;μt为湍流黏度;ε为湍流耗散率;σk为湍动能影响系数;σε为湍流耗散率影响系数;c1ε,c2ε为模型常数。
1.3 数值计算方法及边界条件
本文采用有限体积法对控制方程进行离散,各控制方程中对流项采用一阶迎风格式,将动量方程和连续性方程联立,采用SIMPLE算法求解出各个变量。工质为水,水温为20℃,运动粘滞系数υ=1.007×10-6m2/s,入口边界条件设置为速度进口,分别取3 m/s、6 m/s和9 m/s,以保证水流为高雷诺数下的紊流状态,出口为大气压强。
雷诺数计算公式为:
(5)
式中,Re为雷诺数;v为流速;d为管道直径;υ为运动黏滞系数。
由式(5)可得到该参数下的雷诺数范围为30万到90万。采用无滑移的固壁边界,并用标准壁面函数法对其进行处理。
1.4 网格划分
模型采用内径为100 mm的管道,如图2所示。水流从入口进入,经过平面双弯头管道,产生紊动漩涡,再经过Zanker型流动调整器,最后流向出口。其中,入口直管段长度为1 000 mm,出口直管段长度为2 000 mm,弯头半径为150 mm。

图2 模型结构示意图Fig.2 Structure diagram of model
由于流动调整器的结构较复杂,采用结构性网格不利于块体的切割,所以采用非结构性网格,网格数约60万,且流动调整器部分采用局部加密。具体网格划分如图3所示。
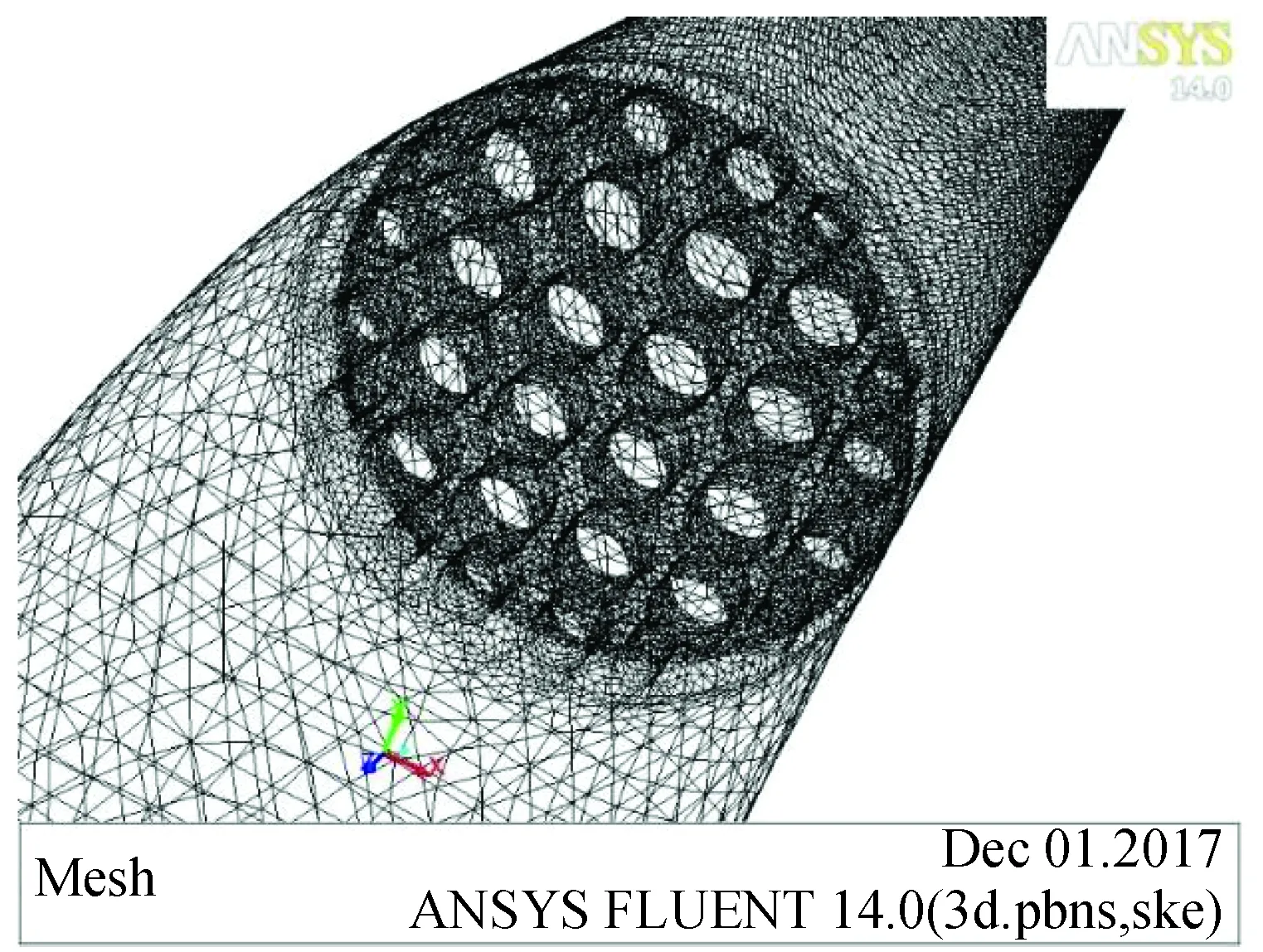
图3 管道网格划分Fig.3 Pipeline mesh generation
2 数值模拟结果及分析
由于平面双弯头的作用使水体产生了流速畸变,水流的流速分布不再呈对称的稳定分布。本文定义沿管道水流方向观测,凸出侧为凸侧,凹进侧为凹侧,水流方向由左向右,如图4所示。由图可知,进入双弯头后水体的高速部分一直位于管道的凸侧,在凹侧的水体流速较慢,流场存在明显的畸变。x/D为沿轴向分布的不同位置,x为距流动调整器出口的距离,D为管道直径。

图4 平面双弯头管道流速分布云图Fig.4 Flat double elbow pipe flow velocity distribution
2.1 有、无流动调整器时截面流速分布
图5为各个工况下x/D=3时的横截面速度分布云图。由图可知,不加设流动调整器时截面的速度分布与加设流动调整器时截面的速度分布相差甚远。无流动调整器时,流体的紊动程度随流速的增加而增大,但流速的增加对速度分布规律的影响并不大。而对于加设流动调整器的情况,随着流速的增大,流场的畸变程度并没有明显增大,流速更趋于充分发育阶段的分布。但是,由于Zanker型流动调整器的柱状孔,导致水体产生淹没射流,Zanker型流动调整器的特有结构使水体的流速在中间部分与充分发育的紊流流速分布稍有差异。
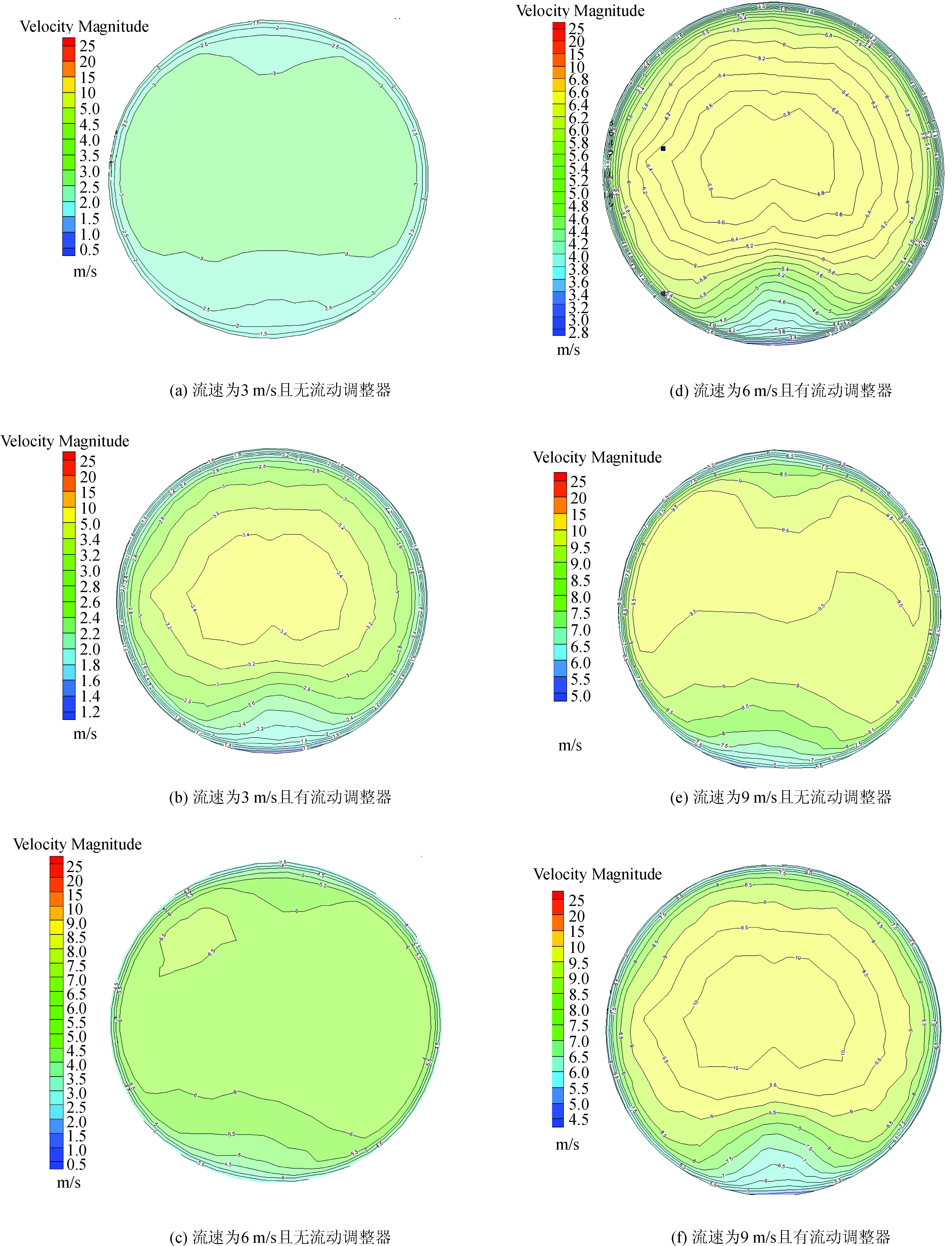
图5 不同工况下横载面速度分布Fig.5 Cross section velocity distribution under different working conditions
2.2 竖直径向流速分布
图6至图7为入口流速为9 m/s时有、无Zanker型流动调整器情况下径向流速v随x/D增加的分布特征。由图6可以看出,无流动调整器时,管道横剖面上的径向流速小于充分发育的紊流流速,随着距离的增加,这种趋势慢慢减小,最后在x/D=15时才达到充分发育的紊流流速。由图7可以看出,加设Zanker型流动调整器时,x/D=9时的速度分布已经十分接近充分发育的湍流流速分布,x/D=12时的流速分布与充分发育的流速分布完全吻合。充分发育的紊流流速分布由相同工况下长直管道流场的数值模拟计算得到。

图6 无流动调整器时竖直径向流速分布Fig.6 Vertical redial flow velocity distribution without flow regulator

图7 加设流动调整器时竖直径向流速分布Fig.7 Vertical redial flow velocity distribution with flow regulator
Zanker型流动调整器的结构是对称的,且由图6、图7分析可知,管道流速分布沿竖直径向基本对称,而中轴位置附近的流速变化更明显,为了充分观察这种流速的变化过程,取竖直径向上位于中心点下方0.01 m处(即r=-0.01)的速度来分析不同工况下的流速变化规律,如图8所示。
由图8可以看出,由于紊流各流层相互掺混的能量交换作用,平面双弯头产生的速度脉动和二次流的能量不断被消耗且不可逆,随着距流动调整器出口距离的增加,流速都会趋于充分发育阶段的分布状态。对比有无Zanker型流动调整器情况下的流速变化可以看出,流动调整器对存在流态畸变的流场具有很明显的调节作用。分析以上结果可以发现,流速的变化与水流的速度波动程度没有直接的关系,这是由于水流处于阻力平方区,沿程水头损失系数与雷诺数无关,所以流速的变化对能量交换的影响不是很明显,即入口流速对沿程速度的变化影响不是很大。
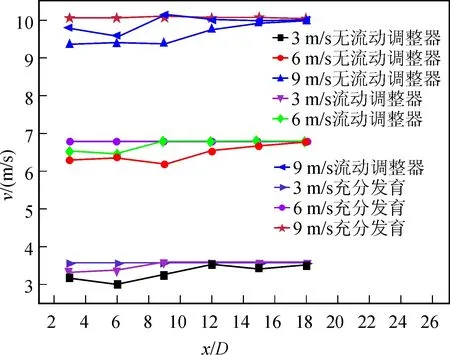
图8 不同工况下r=-0.01 m处的流速变化Fig.8 Change of flow rate under different conditions at r=-0.01 m
3 结 论
1) 不加设流动调整器时截面的速度分布与加设流动调整器时的速度分布相差甚远;无流动调整器时,水体随着速度的增大紊动程度增加,而加设流动调整器时,流速更趋于充分发育阶段的分布;
2) 在平面双弯头后面加设流动调整器可以使流场快速达到充分发育时的分布状态;在管道存在流态畸变时,若不加设流动调整器,会使管道内的流场畸变传播很长一段距离,从而影响测量仪器的测量精度;
3) 竖直径向流速分布随入口速度的增大而变大,但速度的相对变化值基本保持不变,在阻力平方区下,雷诺数即流速对流场的影响不大。
