奇异分数阶Laplacian方程弱解存在唯一性的算子方法
2018-10-29彭达瑶秦新强
王 兴,彭达瑶,秦新强,胡 钢
(西安理工大学理学院,陕西西安710054)
随着现代科技的发展,经典的Laplacian算子在描述物理、化学、生物甚至是金融学中的新现象和新规律时具有很大的局限性。上世纪八十年代以来,随着相变理论、反常扩散、共形几何、非牛顿流体以及金融财务优化等领域的发展[1-4],研究人员发现分数阶Laplacian方程相较于整数阶微分方程能更好地描述涉及记忆模式、遗传效应以及路径依赖和具有全局相关性的物理过程。因此,近些年来,分数阶微分方程理论及应用受到许多学者的广泛关注,其研究得到了迅猛发展。
本文将研究一类含有奇异非线性项的分数阶椭圆问题(1)解的存在性与唯一性:
(1)
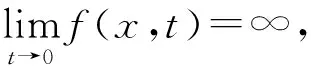
有关N维欧氏空间RN上分数阶Laplacian算子的定义以及分数阶Sobolev空间理论等内容,可以参见文献[5]。

(2)

相比于奇异Laplacian方程,针对奇异分数阶Laplacian方程的研究还较少,有许多根本性问题需要探索。2014年Fang在文献[11]中考虑了如下奇异分数阶Laplacian方程:
(3)
其中0
(4)

在我们已有工作的基础上,本文研究奇异项为一般形式f(x,u)∈Lp(Ω×(0,∞))的分数阶Laplacian方程,给出方程弱解存在性和唯一性的新方法——算子方法。首先,注意到算子(-Δ)s具有非局部性。Caffarelli和Silverstre在[13]中,通过将(-Δ)s在高一维空间RN+1中进行调和延拓,实现了分数阶Laplacian算子(-Δ)s在一定意义下的局部化,由此可以将问题(1)的求解转化为寻求问题(5)的弱解。因此,提供了利用整数阶椭圆方程理论研究分数阶Laplacian方程的新途径。为了定义方程(1)的弱解,现给出边值问题:
(5)

1 预备知识和主要结果


(6)

下面给出本文需要用到的Banach空间算子理论的部分定义和结果,该部分内容可参见文献[15-16]。
假设E是一个实Banach空间,θ是E的零元。
(a) 若闭凸集P⊂E满足以下两个条件,则称P为闭锥。
① 当x∈P,λ>0时,λx∈P。
② 若x∈P,-x∈P时,x=θ。
(b) 如果闭锥P的内点集Int(P)≠∅,则称P是体锥。
(c) 定义E上的偏序x≤y等价于y-x∈P。若存在一个常数K>0,使得对于所有的θ≤x≤y∈E,有‖x‖≤K‖y‖,则称P是正规锥。
(d) 如果当x≤y∈E时,有Tx≤Ty(Tx≥Ty),则称算子T:E→E是递增(递减)的。
(e) 设x,y∈E,若存在λ,μ>0使得λx≤μy则称x~y。
定义凸集Ph={x∈E|x~h}。显然∀λ>0,有λPh=Ph。
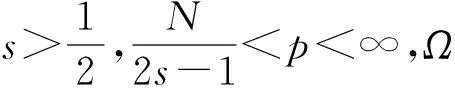
下面给出关于算子方程的一个抽象结果,它是文献[15]中定理2的简单推广。
定理1(见文献[15])假设P是正规锥,算子A满足以下条件:
1) 算子A:Ph→Ph是递减的;
2) 对于任意x∈Ph以及t∈(0,1),存在β(t)∈(0,1)使得A(tx)≤tβ(t)Ax;
3) 存在一个常数l≥0使得x0∈[θ,lh],则算子方程x=Ax+x0在Ph中有唯一解。
注:在文献[15]的定理2.2中,取算子A的负算子-A,其余条件作相应的调整即可得定理1。
在定理1的基础上给出本文的主要结果。
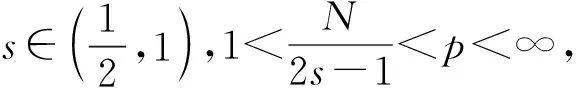
1)f(x,t)在Π=Ω×(0,+∞)上非负;
2) 对于任意R>0有f(x,t)∈Lp(Ω×(0,R));
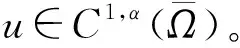
2 问题(1)正弱解的存在性与唯一性
定理2的证明


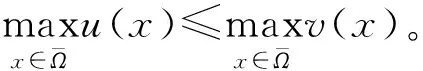



(7)
接下来首先考虑问题(1)对应的分数阶线性椭圆边值问题:
(8)
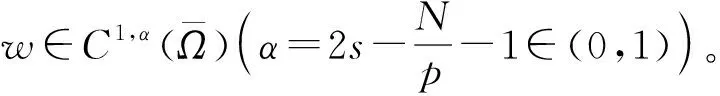
事实上,因为u∈Pφ1,所以由Hopf极值原理得:存在充分小的常数C1∈(0,1),使得
(9)
成立。因此,由定理2条件2)得f(x,u(x))∈Lp(Ω)。从而:
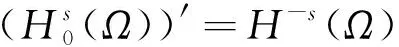
因此,由分数阶Sobolev空间性质知,存在实数列{fk}使得:
(10)

(11)
且tr(v)=w。
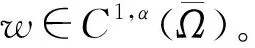
第二步:首先,由第一步的结论可以定义算子A:Pφ1→E为:
Au=w,u∈Pφ1
(12)
下面证明集合Pφ1是算子A的不变集,即:
A:Pφ1→Pφ1
(13)
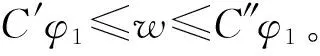
设函数η是分数阶线性椭圆问题(8)当u=φ1时的正弱解,即:
(14)
所以
Aφ1=η
(15)

(16)
并且:

(17)
上述不等式表明,对于分数阶线性椭圆问题(8)在弱意义下有不等式:
(-Δ)sw=f(x,u(x))≤φ(C1)f(x,φ1(x))=
(-Δ)s(φ(C1)η(x))
(18)
和:
(19)
成立。因此,由分数阶线性椭圆问题的比较原理(参见文献[5]中引理4.6)得:

(20)
由特征函数φ1的正则性和Hopf极值原理,存在常数C2,C3>0使得:

(21)
其中d(x)=d(x,∂Ω)是x到边界∂Ω的距离。
|w(x)-w(y)|≤C4|x-y|
(22)

(23)
接下来证明存在C5>0使得:
(24)
(25)
且:
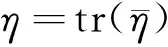
(26)
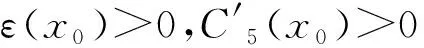
∀x∈Bε(x0)(x0)∩Ω
(27)
因为∂Ω是紧集,应用有限覆盖定理,可选取有限个点x1,x2,…,xK∈∂Ω使得:
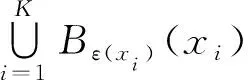
(28)
令:
ε=min{ε(x1),ε(x2),…,ε(xK)}
则对于任意x∈{x|d(x,∂Ω)≤ε},均存在开球Bε(xi)使得x∈Bε(xi)∩Ω,从而有:

(29)
再结合不等式(20)~(24)得:
(30)

(31)
即w(x)∈Pφ1。因此证明了集合Pφ1是算子A的不变集。
第三步:首先,设u1,u2∈Pφ1且u1≥u2,则由定理2的条件3)得:
f(x,u1(x))≤f(x,u2(x))
(32)
由分数阶Laplacian方程的比较原理得:
A(u1)≤A(u2)
(33)
因此,算子A是递减的,即满足定理1的条件1)。
其次,证明对于任意u∈Pφ1,λ∈(0,1),有:
A(λu)≤φ(λ)u
事实上,由问题(8)弱解的存在性以及算子A的定义我们有:
(34)
以及:
(35)
又由定理2的条件3),可得:

因此,用式(34)减式(35)得:
(36)
进而由比较原理得:
A(λu)≤φ(λ)A(u)
(37)
因为:
λ∈(0,1),φ(λ)∈(λ,1]
(38)
所以:
(39)
将式(39)带入式(37)得:
(40)
式(18)满足定理1的条件2)。
最后,取x0=θ显然有θ∈[θ,φ1],满足定理1的条件3)。
综上,根据定理1得算子A存在唯一不动点u∈Pφ1,即问题(1)有唯一的正弱解:
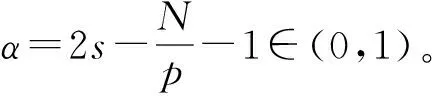
定理2证毕。
