双区静电除尘器的数值模拟研究
2018-10-29高梦翔张益坤施建伟上官文峰
高梦翔,姚 鑫,朱 勇,张益坤,施建伟,上官文峰
双区静电除尘器的数值模拟研究
高梦翔,姚 鑫,朱 勇,张益坤,施建伟,上官文峰*
(上海交通大学机械与动力工程学院,上海 200240)
采用数模拟的方法研究了双区静电除尘器内流场分布、颗粒荷电及颗粒运动等难以直接测量的物理过程,构建了双区静电除尘过程完整的数值模型.采用泊松方程、电流连续性方程和匀强电场方程描述电场,采用N-S方程和雷诺应力标准湍流模型描述流场,采用拉格朗日法描述颗粒运动轨迹.通过截面风速与颗粒去除率的模拟值与实验值的对比,验证了数值模型在模拟内部流场和颗粒运动时的准确性.数值模拟结果表明:双区静电除尘器内部流场分布对入口风速的变化非常敏感;颗粒荷电方式占比由颗粒粒径决定;荷电区内颗粒向极板的趋近过程由流体曳力和电场力共同完成,收尘区内的趋近过程则由电场力主导;入口流速通过改变颗粒前进速度和内部流场形态来影响颗粒运动轨迹.
双区静电除尘;数值模拟;流场分布;除尘效率
近年来,我国多数城市大气污染严重,以PM2.5为代表的空气细颗粒污染物引起社会广泛关注[1-2].面对这一健康威胁,室内空气净化器成为越来越多人的选择.而静电除尘器(ESP)因效率高、阻力小和无耗材的特点受到关注,其在室内空气净化领域的潜力正被挖掘和研究[3].
常用的电除尘器按结构可分为单区和双区,区别在于前者内部颗粒的荷电和捕集过程同时进行,而后者颗粒荷电和捕集过程则分别在荷电区和收尘区完成.单区ESP结构简单,处理流量大,常应用于工厂尾气处理.但内部电流体的作用使其对小粒径颗粒的捕集效果较低[4],臭氧发生率也较高[5],不适用于室内空气净化.相较而言在这两方面表现更优的双区ESP更能满足室内空气净化的需求[6-7].
近年来研究者对双区ESP的研究重点在于超细颗粒物去除率的提升,研究方向可归纳为材料开发、结构设计和参数优化.例如使用新的放电极材料或对收尘极表面包裹泡沫材料,以强化颗粒荷电过程或减少二次扬尘现象,使超细颗粒物去除率得到提升[8-9].此外也有学者对双区ESP的结构进行研究,目标主要为颗粒凝并结构的设计,使超细颗粒在荷电的同时凝并长大,降低超细颗粒物的捕集难度[10].另外有学者专注于双区ESP的参数优化,测定放电极电压、供电方式(AC/DC)、入口风速和颗粒粒径与颗粒去除率的关系,探讨ESP电源参数的设定原则[11-12].
然而上述关于双区ESP的研究均停留在实验现象层面,仅关注实验条件与颗粒去除效率的关系,缺乏对于双区ESP内部颗粒运动过程的认识.双区静电除尘的实际物理过程非常复杂,内部电场、流场和颗粒物相互耦合,一种物理量的改变会引起其他物理量的变化,因此改变单一实验条件以观察颗粒去除率增减的做法很难反映现象背后的原理和逻辑.应当对双区静电除尘过程建立完备的数学模型,研究内部的颗粒运动过程,对颗粒荷电特性进行定量分析,才能深入认识这一物理过程及指导后续设计.
本文提出了一种双区ESP数值模型的构建方法,建立了其内部流场与颗粒运动的二维数值模型,对流场采用时均N-S方程和雷诺应力标准湍流模型求解,对颗粒运动采用拉格朗日法求解.为验证数值模型,模拟计算了一个线板式双区ESP内部流场和颗粒轨迹,截面风速和颗粒去除率的模拟值与实验值均相吻合.在验证模型后,进一步分析了双区ESP内部流场分布、颗粒荷电特性及颗粒运动轨迹,研究了入口风速对颗粒轨迹的影响方式.
1 数学模型与数值方法
1.1 电场模型
忽略气流和颗粒对电场的影响,荷电区电晕放电电场的空间分布满足泊松方程和电流连续方程[13]:
×(0)=×(-0Ñ)=(1)
×= 0 (2)
式中:为荷电区电场强度,V/m;为电流密度,A/m2;为电势,V;为荷电区空间电荷密度,C/m3;0为气体介电常数,8.85×10-12C2/(N·m2).方程(1)和(2)的边界条件如表1所示,其中w为放电极电势,w为放电极表面空间电荷密度,可基于Kaptzov假设和Peeks公式计算.

表1 荷电区电场边界条件
收尘区由多个带电平行极板组成.忽略边缘效应及流体内电荷的影响,可认为极板间电场强度大小相等,方向由正极板垂直指向接地极板.收尘区内电场满足匀强电场方程:
c=/(3)
式中:c为极板间电场强度,V/m;为正负极板间电势差,V;为极板间距,m.
1.2 流场模型
荷电区内流体中的大量电荷使流体本身在强电场作用下受到电场力,因此荷电区内的流场也被称为电流场.假定放电极产生的电荷仅存在于荷电区而不进入收尘区,忽略收尘区内电场对流场的作用.已有的研究表明[14]荷电区和收尘区内流场可以用时均Navier-Stokes方程和雷诺应力标准湍流模型[15]求解.时均Navier-Stokes方程可以写作如下形式:
×= 0 (4)
f(×)=-(+t)2+ci(5)
式中:为流体速度,m/s;f为流体密度,kg/m3;为层流黏性系数,kg/(m·s);t为湍流黏性系数, kg/ (m·s);为压力,Pa;ci为流体受到电场的体积力, N/m3,荷电区内此项计算方式如方程(6)所示,收尘区内此项为零.
ci=(6)
对于方程(4)~(6),其边界条件包括荷电区入口处的指定速度(in)、收尘区出口处的指定压力(1atm)、荷电区和收尘区内的标准壁面函数.
1.3 颗粒荷电模型
为兼顾计算的准确性和便捷性,考虑颗粒两种荷电方式,选择荷电量随时间变化的模型[16-17]:
p() =field+diffusion(7)
对于电场荷电,其荷电量表达式为:
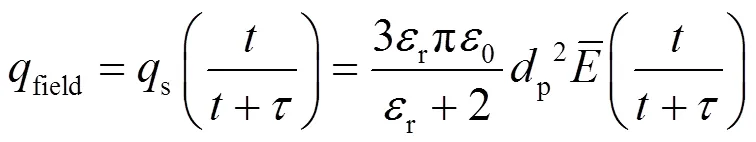
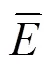
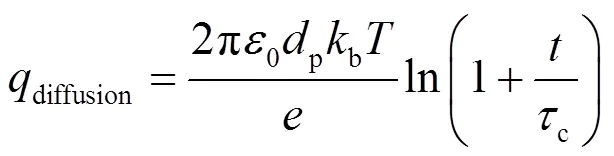
式中:b为Boltzman常数,1.38×10-23J/K;c为扩散荷电时间常数,s.
1.4 颗粒运动模型
忽略颗粒物之间的相互作用,采用拉格朗日模型计算带电颗粒在静电除尘器内的运动轨迹,考虑曳力和电场力对颗粒的影响,静电除尘器内颗粒受力方程如下[18]:
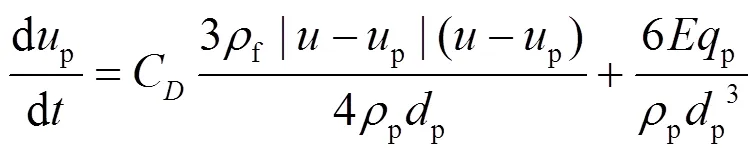
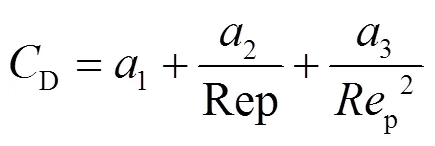
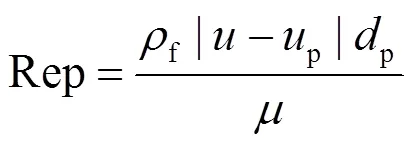
式中:p为颗粒运动速度,m/s;p是颗粒密度,kg/m3;p是颗粒荷电量,C.
上述静电催化耦合系统的电场、流场、颗粒荷电和颗粒运动模型通过软件COMSOL求解.
2 数值模型的实验验证
2.1 实验装置
风道含风机、风道主体、荷电区和收尘区等部分.风道入口处设有气体整流装置,其后依次布置荷电区和收尘区.从中间高度截取剖面,此剖面即二维数值模拟的计算对象,如图1所示.风道主体侧面设有3个依次编号的采样口,分别位于荷电区和收尘区前后.荷电区中央有直径为0.22mm的电极线,通过高压绝缘电线导出连接10kV的高压电源,极板接地;收尘区中央极板接5kV高压电源,其余极板接地.
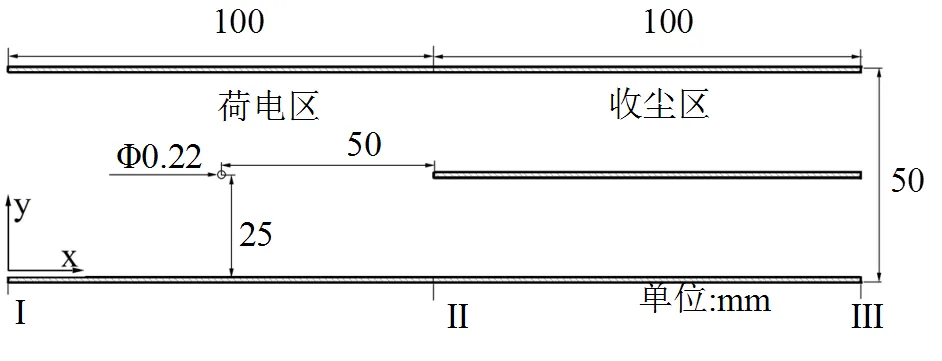
图1 数值模型的几何参数
采用自由剖分三角形的方式生成网格,对电极线处网格进行加密处理.分别选取13261、20628、69874为网格单元数模拟相同除尘过程以验证网格无关性,除尘效率的相对误差不超过2%,选取网格数为69874时的网格划分,电极线处及整体网格如图2所示.

图2 实验电除尘器网格划分示意
2.2 验证方法与结果
流场的验证如下:调节风机功率使气流以0.5m/s的速度通过实验风道的采样口Ⅰ截面,使用TSI 9545型热线式风速仪在采样口Ⅱ、Ⅲ处沿方向测量0,10,20,25,30,40,50mm处的风速并记录.数值模型中代入电极线电压等相关边界条件及物性参数,计算后导出Ⅱ、Ⅲ截面的风速模拟曲线并与实验测量值对比.由图3可知两个采样口截面风速的模拟值与实测值符合良好,双区ESP流场的数值模拟结果可信.
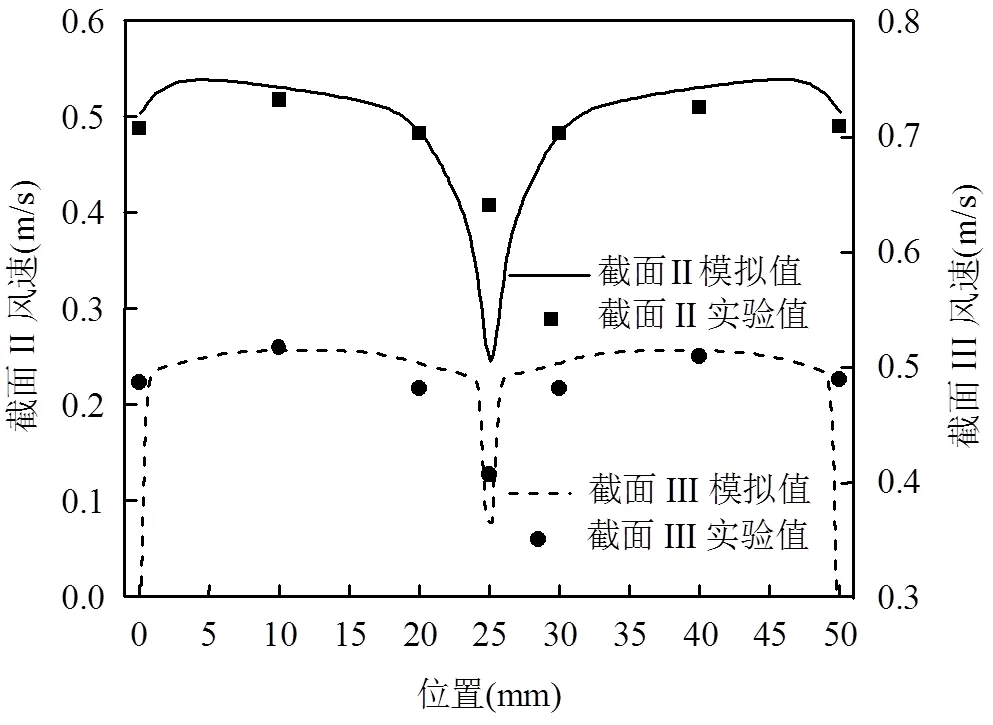
图3 风速实验值与模拟值对比
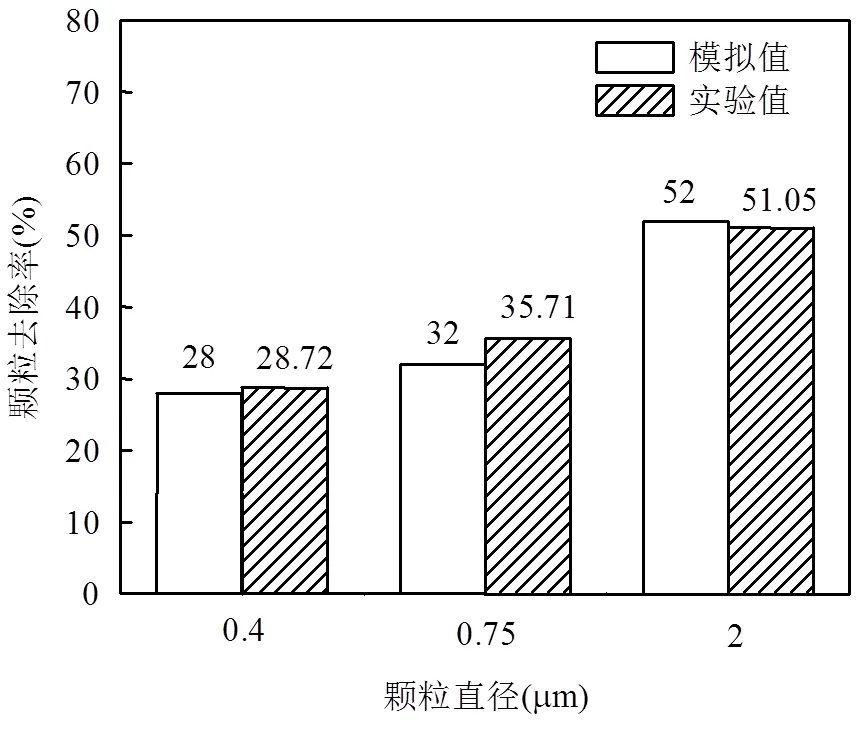
图4 颗粒去除率实验值与模拟值对比
除尘效率的验证如下:向实验风道输送混合均匀的带尘气流,使其依次通过荷电区和收尘区,在采样口Ⅰ和Ⅲ处使用苏州自动化仪器仪表研究所的CSJ-D型全半导体激光尘埃粒子计数器测量风道中心0.3~0.5μm、0.5~1μm和1~3μm 3个粒径段颗粒的数量浓度,统计采样口Ⅰ和Ⅲ处的颗粒浓度差以计算ESP除尘效率的实验值.在数值模型中设定颗粒基于入口截面网格释放,初速度与气流入口速度相同,选取测量粒径段平均直径0.4,0.75,2μm为颗粒直径,烟尘平均密度2200kg/m3为颗粒密度进行模拟,统计落在荷电区和收尘区极板上的颗粒数量以计算除尘效率的模拟值.由图4可知,各粒径颗粒的除尘效率模拟值与实验值符合良好,双区ESP的颗粒去除率随颗粒粒径的减小而迅速下降.
通过流场及颗粒去除率的实验验证可知,本文提出的数值模型可以精准模拟双区ESP的除尘过程,无论内部流速分布还是除颗粒物效率均与实测值非常接近.
3 结果与讨论
3.1 流场的讨论
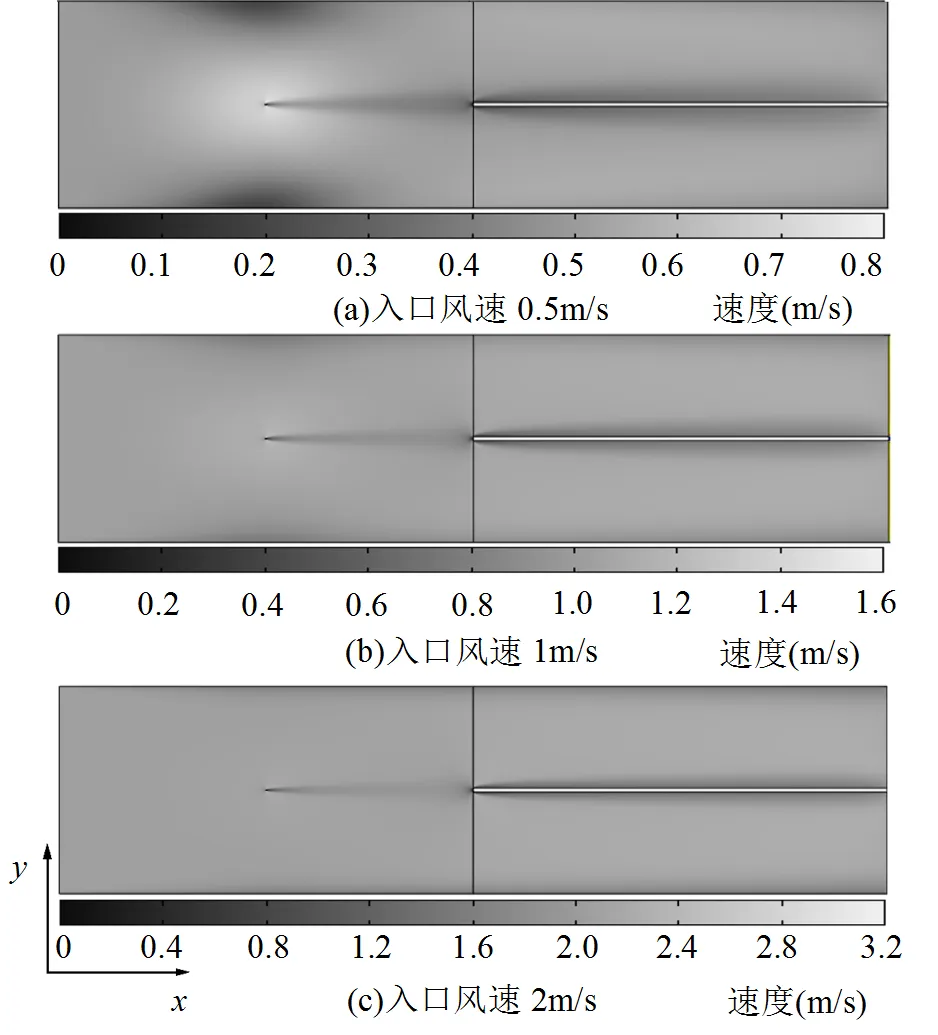
图5 双区ESP速度分布
仅改变入口风速这一边界条件,得到不同入口风速下双区ESP内部的流速分布.如图5所示,荷电区内强电场和大量带电离子使流体受到电场力的作用,运行过程中的双区ESP内部流场并不均匀.气流进入荷电区入口后,在轴上受到电场力的方向在电极线上游与方向相反,在下游与方向相同,而轴上流体始终受到电极线朝向极板的电场力作用.因此电极线前的流体被迫偏离极板,电极线周围流速升高,极板处流速降低.而电极线后的流体则加速流向极板,形成了电极线下游的带状低速区.
对比图5(a),(b),(c)可知,双区ESP内部流场形态对入口风速非常敏感.随着入口风速增加,荷电区极板中央低速区逐渐消失,电极线下游带状低速区逐渐变窄,流场迅速变均匀.依据电流体相关理论可解释此现象,荷电区内电场力对流场的影响可用无量纲数EHD衡量,此无量纲数为流体受电场力与自身惯性力的比值,其值越大,电场力对流体的影响越显著.
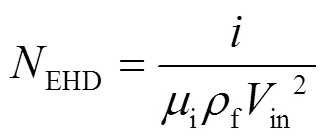
式中:为单位长度电极线的放电电流,i为离子迁移率.由公式可知,EHD的值与in2成反比,入口速度的增加会大幅降低流体受电场力的影响,使得电场力导致的流场畸变迅速恢复.
3.2 颗粒荷电的讨论
数值模拟计算完毕后,导出荷电区内颗粒运动过程中的荷电量数据,绘制颗粒荷电特性曲线及颗粒荷电方式占比,如图6及图7所示.
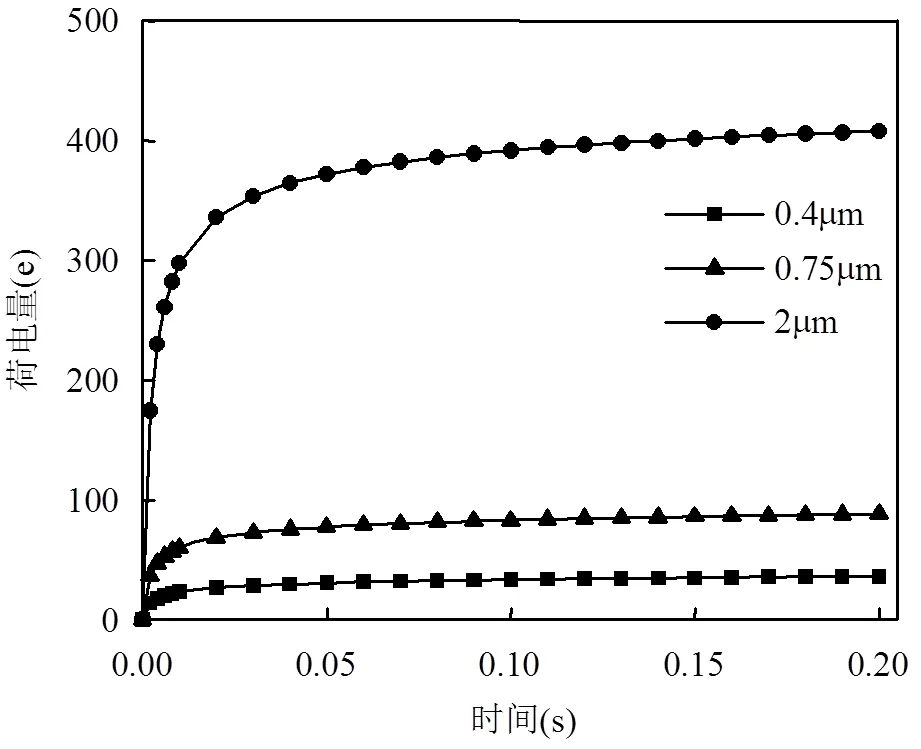
图6 颗粒荷电特性曲线
由图6可知,颗粒物荷电量在短时间内迅速增加,随后持续稳定上升.截至荷电完毕,颗粒总荷电量随着粒径的减小而减小.结合颗粒荷电模型分析,荷电特性曲线反映了电场荷电和扩散荷电这两种不同荷电方式的作用效果.电场荷电的作用体现在短时间内荷电量的快速增加,增加至上限(电场饱和荷电量)即停止.而扩散荷电的作用体现在荷电量的持续增长,其增长速率虽缓,扩散荷电量却可随时间无限增加.
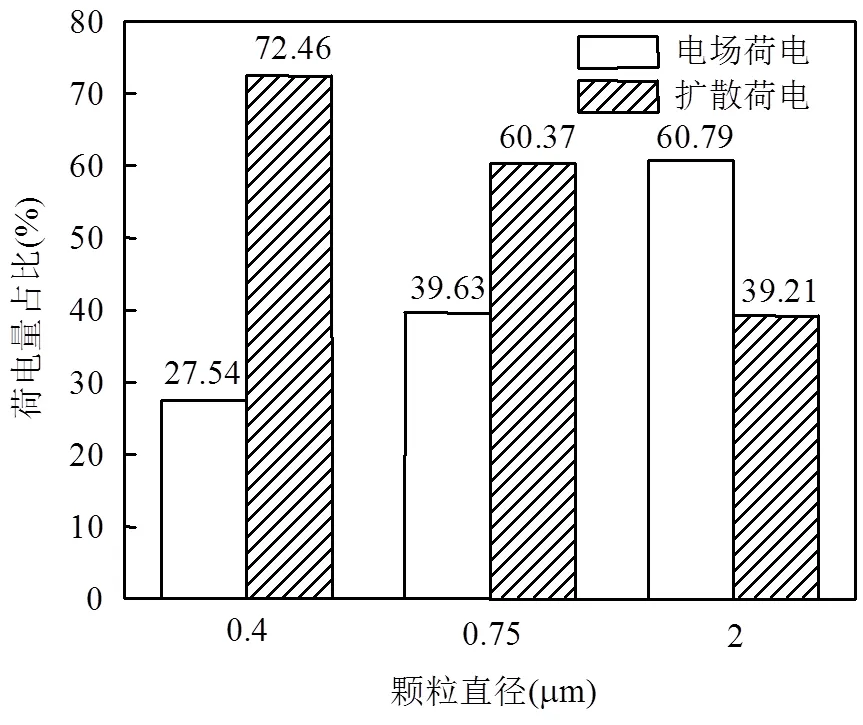
图7 颗粒总荷电量中2种荷电方式占比
由图7可知,电场荷电是2μm颗粒主要荷电方式,扩散荷电是0.4μm和0.75μm颗粒主要荷电方式,颗粒粒径越大,电场荷电所占比重越大,颗粒粒径越小,扩散荷电所占比重约大.针对两种荷电方式的作用特点,可对于不同粒径大小的颗粒提出不同的优化荷电方式.对于以电场荷电为主的2μm及以上颗粒,进入荷电区后其电场荷电量能在短时间内接近饱和,因此增加荷电区内平均电场强度以提高电场荷电量的上限是提升此类颗粒最终荷电量的有效途径.而对于0.4μm及以下颗粒,其粒径决定了电场荷电量在最终荷电量内占比很低,增加荷电区平均电场强度对最终荷电量的收益很小,只有尽量延长其在荷电区内的停留时间才能使此类颗粒最终荷电量稳定增加.
3.3 颗粒运动轨迹的讨论
分别改变入口风速及颗粒粒径,对双区ESP的除尘过程进行模拟.图8为入口风速为0.5m/s时不同粒径颗粒的运动轨迹.由图8可知,双区ESP的荷电区和收尘区均有除尘效果,颗粒去除效率随粒径的减小而降低.按照颗粒轨迹特点,双区ESP的除尘过程可分为荷电区内和收尘区内2个阶段.荷电区内颗粒向极板的趋近过程受电流体曳力和电场力共同影响,中央颗粒在流体曳力和电场力的合力作用下加速向下游前进,靠近两侧极板的颗粒则在合力作用下趋近极板,部分颗粒被荷电区极板捕获.收尘区内颗粒向极板的趋近过程主要受电场力控制,颗粒进入收尘区后荷电量恒定,所受电场力恒定并垂直指向极板,收尘区内颗粒轨迹近似直线,颗粒粒径越大,斜线倾角越大,被收尘极板捕获的颗粒就越多.
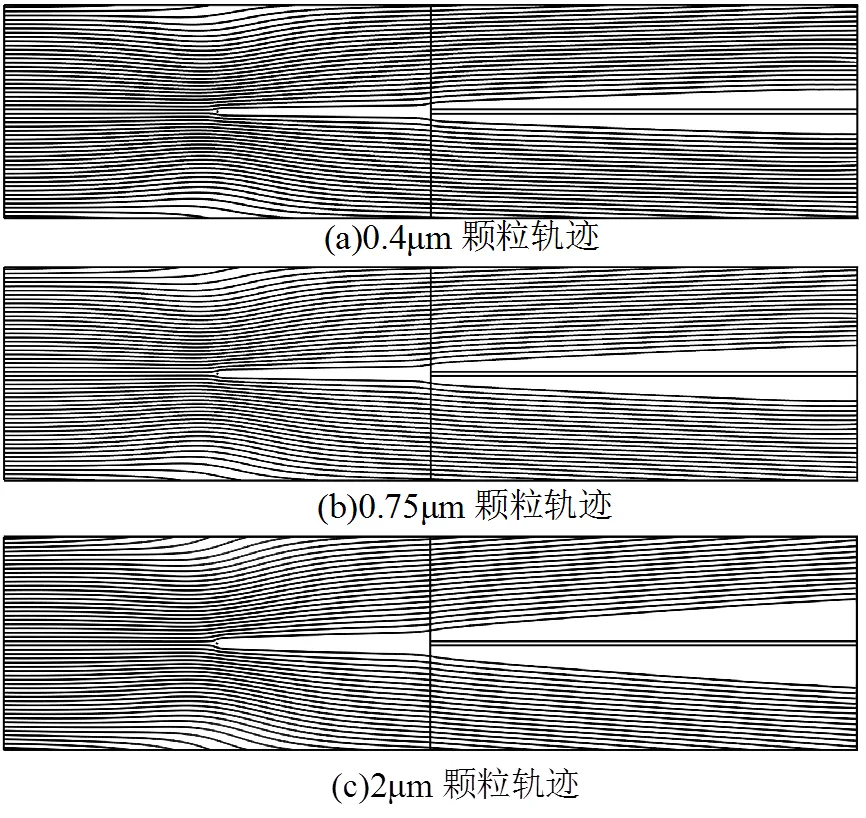
图8 不同粒径颗粒运动轨迹

图9 不同入口风速下2μm颗粒运动轨迹
图9为不同入口风速下双区ESP内部2μm颗粒运动轨迹.结合3.1节所述,可确定入口风速增加对颗粒运动轨迹存在2方面的影响.其一是颗粒在ESP内停留时间变短,电场力对颗粒作用时间减少,缩短了颗粒向极板的趋近距离,导致更少颗粒被极板捕获.其二是入口风速增加引起的流场形态变化会影响颗粒运动轨迹.举例说明,当入口风速为0.5m/s时,图5(a)的荷电区极板中心存在低速区域,颗粒经过此区域时前进速度放缓,电场力对颗粒物的捕集效果增加.这一过程在颗粒轨迹上的体现如图9(a)所示,此区域内的颗粒轨迹呈曲线,极板捕获颗粒的数量较其他区域也更多.而随着入口风速的增加, ESP内部流场由不均匀向均匀转变,存在流速差异的区域消失,颗粒轨迹越来越平直,极板上颗粒的落点分布更均匀.综上所述,研究颗粒物去除率与入口风速的关系时,不能简单认为入口风速只影响颗粒前进速度或停留时间,还应具体分析不同入口风速下ESP内部流场形态,考虑流场形态的变化对颗粒运动轨迹的影响.
4 结论
4.1 构建了双区ESP的数值模型,且数值模型通过了实验验证,截面风速和除尘效率的模拟值均与实验值吻合很好.
4.2 荷电区的强电场和带电离子使双区ESP内部流体受到电场力的作用,电极线周围流速加快,荷电区极板中心流速降低.随着入口风速增加,电场对流场的影响迅速降低,内部流场变均匀.
4.3 颗粒粒径越大,电场荷电量占比越大;颗粒粒径越小,扩散荷电量占比越大.增加荷电区电场强度是提升大粒径颗粒荷电量的有效手段,延长小粒径颗粒在荷电区内的停留时间可使其荷电量稳定增加.
4.4 双区ESP荷电区和收尘区均具有除尘效果.荷电区内颗粒在流体曳力和电场力共同作用下趋近极板,而在收尘区内颗粒向极板的趋近过程由电场力主导,并且随着颗粒粒径的减小,双区静电除尘器的除尘效率明显降低.
4.5 入口风速增加对颗粒运动轨迹的影响并非简单地增加颗粒在双区ESP内的前进速度,其引起的流场形态的改变也会作用于颗粒轨迹.
[1] 李云燕,殷晨曦.京津冀地区PM2.5减排实效与影响因素的门限效应 [J]. 中国环境科学, 2017,37(4):1223-1230.
[2] 李 锋,朱 彬,安俊岭,等.2013年12月初长江三角洲及周边地区重霾污染的数值模拟 [J]. 中国环境科学, 2015,35(7):1965-1974.
[3] 李帮俊,范泽云,张 溢,等.高压静电催化耦合净化空气中的臭氧控制及其室内浓度预测模型 [J]. 环境工程学报, 2017,11(7):4117- 4124.
[4] Skodras G, Kaldis S P, Sofialidis D, et al. Particulate removal via electrostatic precipitators—CFD simulation [J]. Fuel Processing Technology, 2006,87(7):623-631.
[5] Niu J L, Tung T C W, Burnett J. Quantification of dust removal and ozone emission of ionizer air-cleaners by chamber testing [J]. Journal of Electrostatics, 2001,51:20-24.
[6] Hyun O, Baek M, Moon J, et al. Performance evaluation of two-stage electrostatic air filter with low-ozone emission corona charger [J]. Particulate Science & Technology, 2016,35(1):71-76.
[7] Kim H J, Han B, Kim Y J, et al. Submicrometer particle removal indoors by a novel electrostatic precipitator with high clean air delivery rate, low ozone emissions, and carbon fiber ionizer [J]. Indoor Air, 2013,23(5):369.
[8] Kim Y J, Han B, Chang G W, et al. Performance of Ultrafine Particle Collection of a Two-Stage ESP Using a Novel Mixing Type Carbon Brush Charger and Parallel Collection Plates [J]. IEEE Transactions on Industry Applications, 2017,53(1):466-473.
[9] Wen T Y, Wang H C, Krichtafovitch I, et al. Novel electrodes of an electrostatic precipitator for air filtration [J]. Journal of Electrostatics, 2015,73:117-124.
[10] Sobczyk A T, Marchewicz A, Krupa A, et al. Enhancement of collection efficiency for fly ash particles (PM2. 5) by unipolar agglomerator in two-stage electrostatic precipitator [J]. Separation & Purification Technology, 2017,187:91-01.
[11] Jaworek A, Marchewicz A, Krupa A, et al. Dust particles precipitation in AC/DC electrostatic precipitator [J]. Journal of Physics Conference, 2015,646(1):012031.
[12] 沈之旸,郑成航,刘昕涛,等.高温烟气静电除尘中试试验研究 [J]. 中国环境科学, 2018,38(5):1637-1645.
[13] 龙正伟,冯壮波,姚 强.静电除尘器数值模拟 [J]. 化工学报, 2012, 63(11):3393-3401.
[14] Nikas K S P, Varonos A A, Bergeles G C. Numerical simulation of the flow and the collection mechanisms inside a laboratory scale electrostatic precipitator [J]. Journal of Electrostatics, 2005,63(5):423- 443.
[15] Launder B E, Spalding D B. The numerical computation of turbulent flows [J]. Computer Methods in Applied Mechanics & Engineering, 1974,103(2):269-289.
[16] Long Z W, Yao Q. Evaluation of various particle charging models for simulating particle dynamics in electrostatic precipitators [J]. Journal of Aerosol Science, 2010,41(7):702-718.
[17] 周栋梁,李水清,靳 星,等.电场、流场耦合作用下脱除细颗粒物的实验和数值模拟 [J]. 中国电机工程学报, 2016,36(2):453-458.
[18] Yamamoto T, Morita Y, Fujishima H, et al. Three-dimensional EHD simulation for point corona electrostatic precipitator based on laminar and turbulent models [J]. Journal of Electrostatics, 2006,64(7-9): 628-633.
Numerical simulation study of two-stage electrostatic precipitator.
GAO Meng-xiang, YAO Xin, ZHU Yong, ZHANG Yi-kun, SHI Jian-wei, SHANGGUAN Wen-feng*
(School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)., 2018,38(10):3698~3703
A complete numerical model was developed for the dust removal process in the two-stage electrostatic precipitator (ESP). Numerical simulation method was used to study velocity distribution, particle charging characteristics, particle moving tracks and other physical processes which were difficult to measure directly. The electric field was analyzed using Poisson equation, current continuity equation and homogeneous electric field equation. Fluid flow was elucidated using N-S equation and the standard k-ε turbulent model. Particle tracks were described using Lagrangian method.The accuracy of the numerical model was verified by comparing the numerical results with the experimental data of the cross-sectional velocity and the particle removal rate. Numerical simulation results showed that the fluid flow distribution in two-stage ESP was sensitive to the inlet wind speed. The proportion of charge with different charging methods was determined by particle diameter. And the particles of different sizes had different dominant charging methods. Moreover, the approach of particles to plates was caused by the interaction of the electric force and the drag force in pre-charger, while the approach in dust collection part was dominated by electric force. It was also found that the inlet velocity influenced the particle tracks by changing particle advance speed and internal flow field.
two-stage electrostatic precipitator;numerical simulation;fluid flow distribution;dust-removal efficiency
X513
A
1000-6923(2018)10-3698-06
高梦翔(1994-),男,江苏徐州人,上海交通大学硕士研究生,主要从事室内空气净化相关研究.
2018-03-29
国家自然科学基金资助项目(21577088);国家重点研发计划(2017YFC0211805)
* 责任作者, 教授, shangguan@sjtu.edu.cn
