复杂系统工程作业贝叶斯网络风险方法研究
2018-10-29熊娜张孝东李飞马超
熊娜,张孝东,李飞,马超
(1.南昌理工学院,江西 南昌 330044;2.空军勤务学院,江苏 徐州 221000)
0 引言
风险,即损失的不确定性,是指在给定情况下一定时期内可能发生的各种结果间的差异[1-2]。风险管理过程包括风险评估和风险控制2个方面,风险评估可以细分为风险识别、风险分析和风险计划,风险控制可以细分为风险跟踪和风险应对。其中,风险评估是风险管理过程的核心与基础,是实施风险控制的前提。复杂系统工程作业工种多、隐蔽性强、不确定因素多等特点决定了风险的不可避免性,事故发生后的灾难性、社会影响性、难以弥补性等决定了风险管理的重要性。
当前,用于风险评估的方法以定性分析为主,定量分析方法主要包括模糊综合评价、层次分析法、故障树/事件树分析法等。郭发蔚等[3]在获得事件概率风险值的基础上进行了模糊综合评价,确定了风险事件的等级;闫宝会等[4]应用层次分析法和三角白化权函数构建了武器装备研制项目技术风险评估模型;王春雪等[5]通过构建故障树/事件树识别了风险因子,确定了基于贝叶斯网络的燃气管道泄漏致灾风险评估模型。然而,模糊综合评价和层次分析法基于已构建的指标体系,过程繁琐、计算复杂、可拓展性差;故障树/事件树只适合于相对独立事件的二状态分析,难以确定最小割集。
考虑到工艺技术、管理水平、自然环境等诸多不确定因素,本文引入贝叶斯网络理论构建复杂系统工程作业风险评估模型。以贝叶斯理论和图论为基础,贝叶斯网络理论成熟、软件多样,已广泛应用于各工程领域的风险评估与可靠度预测中[6-7]。Marcelo等[8]应用贝叶斯网络对油罐车碰撞事故建立风险评估模型,分析了涉及人可靠性的因素;金灿灿等[9]在确定指标权重的基础上,应用贝叶斯网络构建了航空公司风险评估模型;王刚等[10]从专家群体判断和模糊数学角度描述了多态模糊事件,提出了基于贝叶斯网络的风险概率计算方法。以上文献只是简单地综合专家经验确定条件概率值,文献[11]充分考虑了专家在知识背景、技术水平、逻辑思维等方面不同而造成的不确定性问题,应用DS证据理论和层次分析法确定了多状态贝叶斯网络的条件概率赋值方法。因此,本文将在此基础上应用DS证据理论、三角模糊函数对专家经验信息进行融合处理,建立考虑不确定因素的复杂系统工程作业贝叶斯网络风险评估模型,以提高风险评估的科学性与准确性。
1 工程作业贝叶斯网络风险评估模型构建
1.1 贝叶斯网络模型概述
贝叶斯网络(Bayesian network,BN)表示为BN=(G,θ):网络结构G=(V,A)为有向无环图,节点变量为V={V1,V2,…,Vn}(n≥1),A是弧集合;网络参数θ描述节点间的条件概率关系,用P(Vipa(Vi))表示。对于贝叶斯网络中的有向边(Vi,Vj),Vi为Vj的父节点,Vj为Vi的子节点。节点Vi的父节点用pa(Vi)表示,非后代节点用A(Vi)表示。在给定父节点pa(Vi)的条件下,Vi与A(Vi)条件独立,即[12]
P(Vipa(Vi),A(Vi))=P(Vipa(Vi)).
(1)
贝叶斯网络的联合概率为
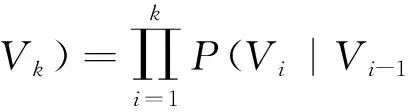
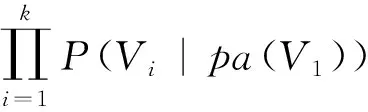
(2)
贝叶斯网络得以广泛应用,基于如下建模优势:
(1) 贝叶斯网络推理以贝叶斯概率理论为基础,算法成熟、软件多样,相对于传统方法,风险评估模型构建简便、运算高效;
(2) 贝叶斯网络结合了概率论与图论优点,清晰直观地表达了节点间的因果关系,实现了先验知识与现场数据的有机结合;
(3) 贝叶斯网络以图形化方式表示了变量间的联合概率分布,充分表达风险因素之间的不确定关联关系。
1.2 贝叶斯网络建模过程
在工程作业风险评估中,贝叶斯网络构建过程如图1所示。
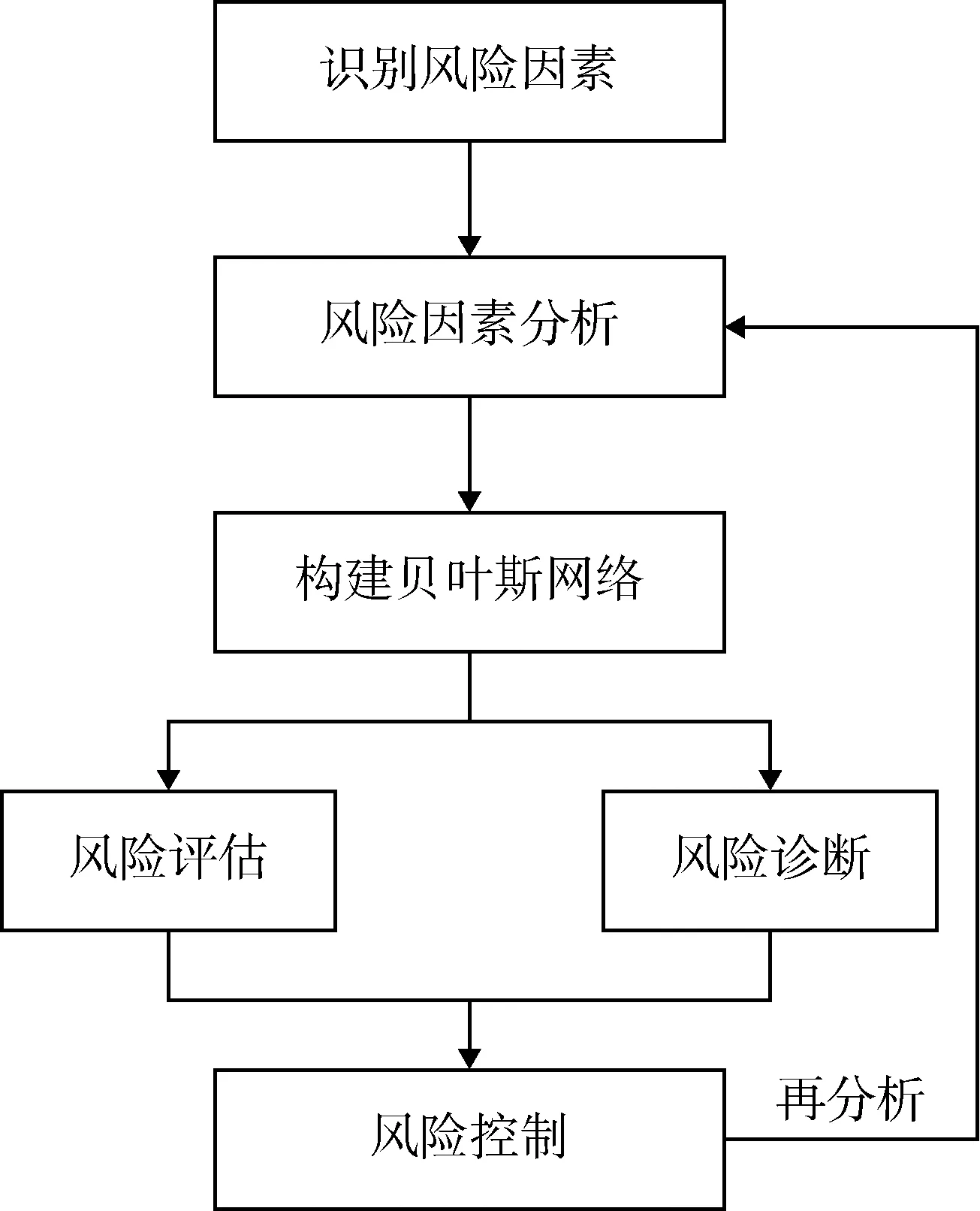
图1 工程作业风险评估建模过程Fig.1 Modeling procedure for risk evaluation in engineering work
(1) 风险因素识别,结合历史统计数据、专家经验,明确在复杂系统工程作业中可能发生的风险事件,对影响事件发生的风险因素进行分析,确定影响因素清单;
(2) 风险因素分析,调查分析确定各个因素发生的可能性大小以及造成损失的严重程度,从中确定主要影响因素;
(3) 构建贝叶斯网络,根据各影响因素之间的因果关系,构建贝叶斯网络风险评估模型,综合各类数据信息确定模型参数;
(4) 风险评估,充分利用贝叶斯网络的因果推理优势,确定在已知概率输入下发生风险的可能性;
(5) 风险诊断,充分利用贝叶斯网络的诊断推理优势,确定在风险发生情况下的关键影响因素;
(6) 风险控制,根据贝叶斯网络评估结果与诊断结果,采取积极有效措施进行重点预防;
(7) 再分析、再评估,工程作业风险评估是一项循环往复的长期工作,根据关键因素的控制程度、新因素的识别信息,对贝叶斯网络模型结构、参数进行更新。
1.3 工程作业风险评估结构模型
复杂系统工程作业工种多、人员多、程序复杂。以安排导弹战备值班为例,包括调拨、运输、启封、检测、维护等多个环节,涉及到运输人员、测试人员、警备人员等多个岗位,作业场地、消防设施、电气设施等多种设施,并且承受振动、冲击、温湿度等多种环境应力影响。受工艺水平、管理水平、自然环境等多种因素影响,在工程作业中隐藏着多种不确定因素,给任务的顺利完成带来了一定的安全隐患:管理层面的缺陷,涉及管人、管物、管理制度;作业层面违章违纪,如违章操作、违章使用工具设备、给后期造成隐患等;装备设施缺陷包括特种设备缺陷、电气设备缺陷、消防设备缺陷等。
在工程作业中,涉及的风险因素可以概括为两大类,人的不安全行为和装备的不安全状态[13]:人的不安全行为分为违章作业、违章指挥、违反劳动纪律、违规着装、违规驾驶和安全管理缺陷6个类别;装备的不安全状态包括装备设施缺陷、安全防护缺陷、自然环境不良和作业场所不良4个类别。各个类别的风险因素集可以继续细分为风险因子,具体如图2所示。根据工程作业各因素之间的层级关系,即可构建风险评估贝叶斯网络模型。
2 贝叶斯网络模型参数确定方法
贝叶斯网络模型参数的确定包括根节点概率取值确定和条件概率值确定。
2.1 基于三角模糊数的根节点概率值确定方法
对于工程作业风险评估模型中多状态节点各状态概率值难以获取的问题,借助专家群决策方法,应用模糊理论进行表达。三角模糊数具有运算简便、应用直观等优点,采用此方法对专家经验进行处理,隶属度函数为
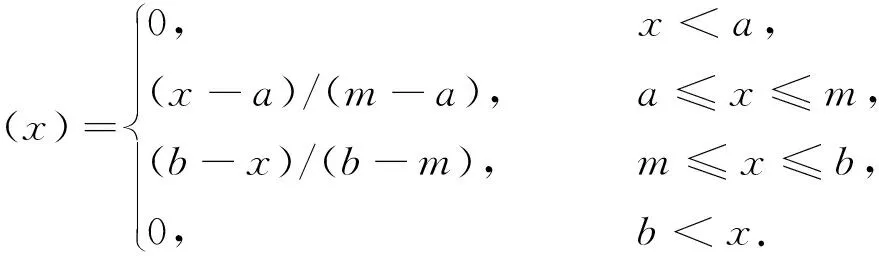
(3)

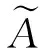
(4)
为了提高专家评判的精度,采用7标度评判,如表1所示,通过7个语义值将专家意见转换为7个模糊概率值。
假设有l个专家对多状态根节点Xi处于状态j的概率值进行语言变量赋值,第k个专家赋值的三角模糊数表示为

(5)
采用算术平均法对专家意见进行综合,则l个专家对节点Xi处于状态j的综合评价模糊概率值为
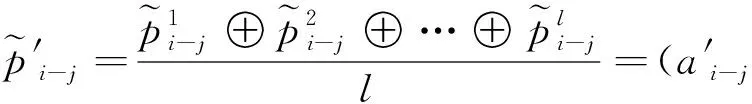
.
(6)

图2 工程作业风险评估因素集Fig.2 Factor set for risk evaluation in engineering work

序号语义值三角模糊数1非常高(0.9,1.0,1.0)2高(0.7,0.9,1.0)3偏高(0.5,0.7,0.9)4中等(0.3,0.5,0.7)5偏低(0.1,0.3,0.5)6低(0,0.1,0.3)7非常低(0,0,0.1)
利用“均值面积法”将模糊概率值转化为精确值,有
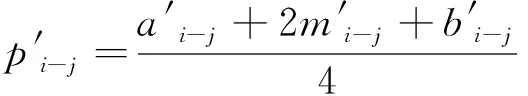
(7)
为确保不同状态概率值之和为1,对根节点各概率值进行“单位化”处理,有

(8)
2.2 基于DS证据理论的条件概率值确定方法
设Θ为变量X的互斥可能值构成的识别框架,其幂集构成集合2Θ。假设∀A⊂Θ,对于集函数m满足2Θ→[0,1],即[14-15]
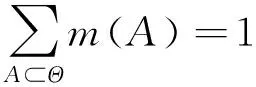
(9)
称m是识别框架Θ上的基本信度分配(BPA),表征证据对事件发生可能性的支持程度。根据基本信度分配确定事件信任函数与似然函数,构造[Bel(A),Pl(A)]信度区间。根据Dempster合成规则对2个mass函数m1,m2进行合成:

(10)
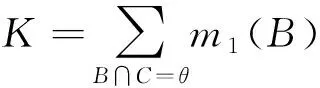
由于各个专家在技术领域、专业水平、文化学历等方面存在差异,构建如表2所示的判断标准,表达专家对多状态贝叶斯网络条件概率关系的判断。假设t个技术专家(e1,e2,…,et)从n个维度(c1,c2,…,cn)对组合对象x1,x2,…,xp作出了相对识别框架Θ的重要度判断,构建了如表3所示的知识矩阵[16-17]。

表3 专家ei在维度cj下的知识矩阵
表3中,1为焦元与自身作比较;0为焦元未作比较;sk为属性cj下的第k个焦元;ak为sk与识别框架Θ的比较系数;pij为领域专家ei在属性cj下占有的权重。
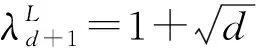
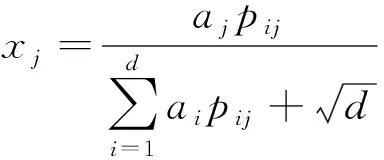
(11)
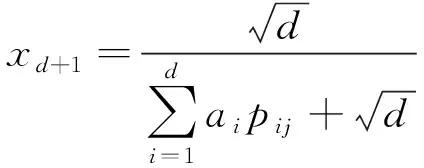
(12)
3 工程作业风险评估仿真分析
3.1 确定贝叶斯网络根节点概率值
为说明本文所研究的方法,假设作业场所不良B4、场所不符合要求B41和作业条件不备B42为4状态节点(4—优、3—良、2—中、1—差),其他节点为2状态节点(2—好、1—差)。咨询4位领域专家判断作业条件是否具备,参照表1建立如表4所示的模糊概率统计表。
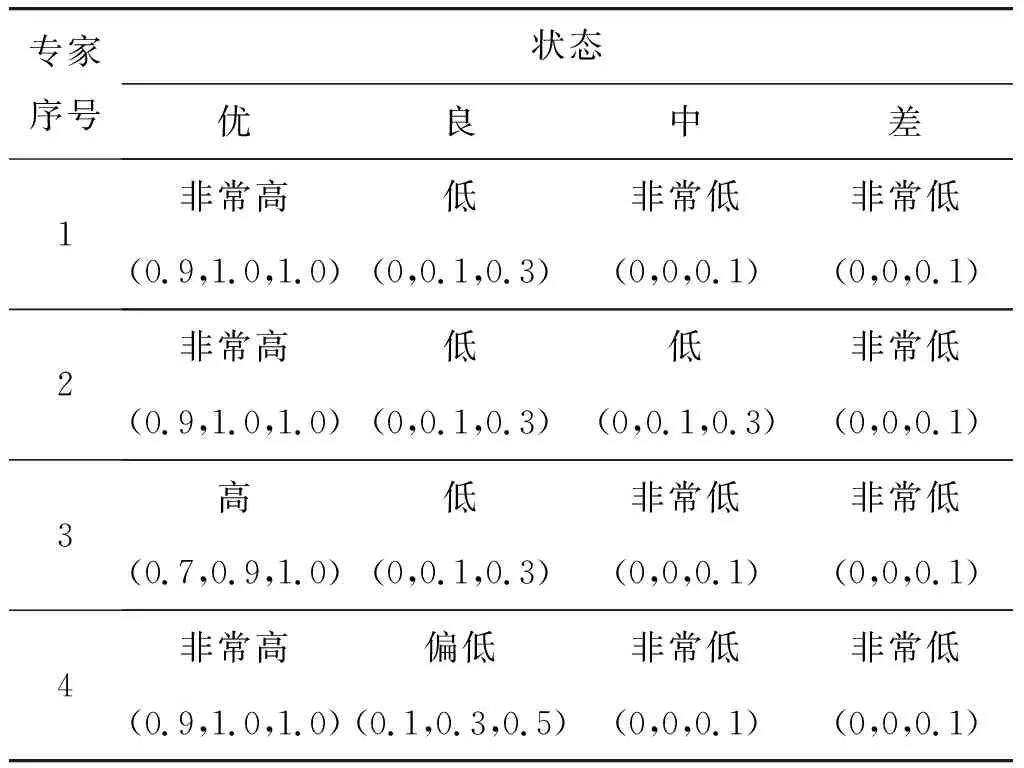
表4 根节点B42各状态专家意见模糊概率
根据式(6)确定节点B42处于各状态的模糊均值为
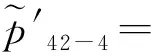
根据式(7)对模糊概率解模糊,有
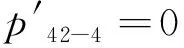
根据式(8)对精确概率“单位化”处理,有
p42-4=0.795 8,p42-3=0.141 4,
p42-2=0.041 9,p42-1=0.020 9.
3.2 确定多状态节点条件概率值
作业场所不良B4的概率分布由场所不符合要求B41和作业条件不备B42确定。在等同对待节点B41和B42的情况下,条件概率值由10个组合确定,分别为:优—优、优—良、优—中、优—差、良—良、良—中、良—差、中—中、中—差和差—差。现以事件“良—中”为例,咨询4位领域专家,假设4位专家权重分别为0.35,0.30,0.15,0.20,建立如表5~8所示的知识矩阵。
参照表3建立表5~8的知识矩阵,通过求解det(Ci-λI)(i=1,2,3,4)最大特征值及相应的特征向量,按照式(10)证据理论合成原则对信度函数合成,结果如表9所示。
可知,节点B4在“良—中”条件下为“优”的概率值为0.048 1,为“良”的概率值为0.413 9,为“中”的概率值为0.418 9,为“差”的概率值为0.074 7,不确定度为0.044 4。
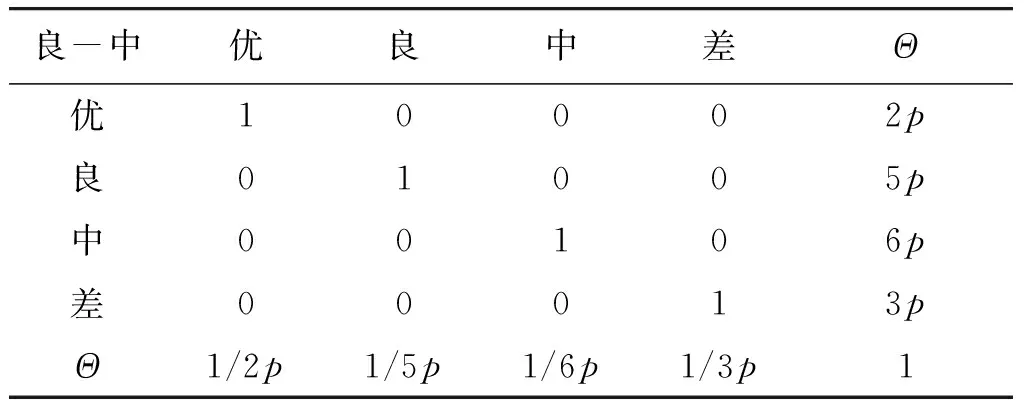
表5 以专家1偏好建立知识矩阵C1
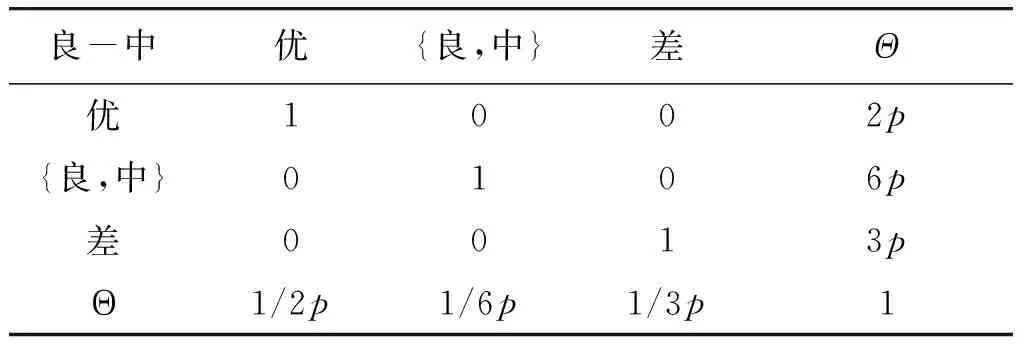
表6 以专家2偏好建立知识矩阵C2

表7 以专家3偏好建立知识矩阵C3
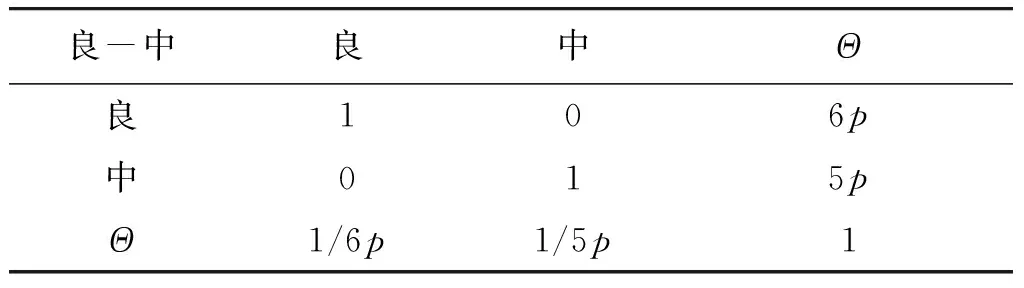
表8 以专家4偏好建立知识矩阵C4

表9 条件概率“良-中”合成结果
3.3 工程作业风险评估结果
利用三角模糊理论综合专家经验、历史统计数据,确定各个根节点的概率值。对于二状态中间节点,根据其与父节点之间的逻辑关系,并考虑不完全覆盖因子,确定条件概率分布。
某分队某次工程作业的风险评估仿真结果如图3所示,其中,天气因素、着装因素、作业因素等各项指标可以根据各次工程作业情况进行确定,在进行风险评估时更改相应的输入即可确定风险指标。利用贝叶斯网络的诊断推理机制即可确定发生风险情况下的关键节点,如图4所示,具体为作业导致隐患、人员管理违章、文件管理违章、武器装备缺陷、特种设备缺陷和作业场所不良。因此,在工程作业实践和专业技能培训中,必须加强对操作人员的业务素质培养、纪律意识教育,并规范各类文档、手册的登记与存放;在战备值班过程中,按时对武器装备、特种设备的维护保养,值班结束及时运回库房保存;优化作业场所条件,尤其是维持好启封、测试库房的温度、湿度,尽量避免承受巨大的昼夜温差。
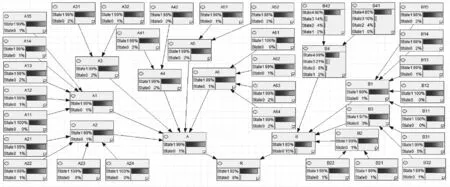
图3 工程作业风险评估仿真结果Fig.3 Risk evaluation result in engineering work

图4 工程作业风险评估诊断分析结果Fig.4 Diagnosis result for risk evaluation in engineering work
4 结束语
复杂系统工程作业涉及多个工种、多个环节、多种不确定因素,本文在风险因素识别、分析的基础上,构建了基于贝叶斯网络的风险评估模型,对工程作业进行风险评估与关键因素确定:
(1) 综合分析某型导弹战备值班涉及的调拨、运输、启封、检测、维护等多个环节,确定了影响任务完成的多个影响因素,构建了基于贝叶斯网络的风险评估模型;
(2) 对于缺乏历史数据的多状态根节点,应用三角模糊函数综合专家经验信息,经求模糊均值、解模糊、单位化确定了节点的输入;
(3) 针对多状态节点条件概率值难以确定的问题,构建知识矩阵,应用DS证据理论进行数据融合,确定了多状态节点的条件概率分布,该方法省去了层次分析法两两比较与一致性检验的繁琐过程,并且将不确定度降低到0.05左右;
(4) 利用贝叶斯网络的因果推理即可确定工程作业的风险概率,利用诊断推理即可确定影响工程作业的关键因子,此外,适当调整参数、增删节点,该网络模型可以应用到今后的工程作业中。
