基于Bootstrap仿真的鱼雷实航工作可靠度评定方法

薛来，甘祖旺

(昆明船舶设备研究试验中心，云南 昆明 650051)

0 引言

鱼雷实航工作可靠度指在规定的实航条件和实航次数内，完成规定功能的概率，其评定一直受到水中兵器行业工程人员和学者的广泛研究。近年来，随着设计水平的提高与制造工艺的进步，鱼雷产品的可靠性越来越高，在可靠性试验中出现的故障也越来越少，传统的基于参试产品个数、故障次数和故障时间的可靠性评估方法在某些时候已不太适用[1]。同时，在工程实践中，由于费用、时间等因素的影响，鱼雷的试验次数往往有限，经典统计方法的评定结果可信度一般比较低[2]。为了缩短置信区间，提高评估结果的可用性，业内多采用补充先验可靠性数据，再与现场试验数据相结合的综合评定方法[3]。目前鱼雷先验数据常使用可靠性预计数据、不同环境下的试验数据及不同研制阶段的研制数据[4-5]。但对于这些数据的转换存在一定的难度，同时转换的可信程度待进一步确认，采用传统可靠性分析理论和方法获得的结果将存在很大的风险[6]。

此外，现有鱼雷先验信息大都局限于非性能可靠性信息[7-10]，而在实际工作中，人们却越来越多地以产品性能下降的程度作为判断故障的依据，也非常关心产品保持其设计性能的能力，性能可靠性[11]数据日益成为评估产品可靠性的重要数据。同时，考虑到Bootstrap仿真方法[12-13]完全依据性能数据样本本身的信息,不需要作任何主观假设,也不需要额外信息,在工程上易于实现。因此，本文提出基于Bootstrap仿真方法的综合性能可靠性信息的鱼雷实航工作可靠度评定方法。

首先，利用Bootstrap方法对已有性能数据样本进行仿真，并评估出性能可靠性；然后，通过Bayes先验分布超参数计算将性能可靠性转换为鱼雷实航工作可靠度的先验数据；最后，结合现场试验数据使用Bayes进行综合评定可靠度。实例表明，该方法可以解决鱼雷实航工作可靠度评定现场试验数据不足的小子样问题，提高评估的准确性。

1 鱼雷性能可靠性评估

1.1 性能可靠性的定义

性能可靠性[11]是指产品在规定工作条件下，规定工作时间内，其性能参数满足规定的允许限要求的概率。本文中以随机变量X泛指产品的任一性能参数。大量试验统计表明，X通常服从正态分布，记为N(μ,σ2)。一般地，用X0±ΔX表示规定的允许限，其中X0称为性能参数的额定值,±ΔX称为性能参数的最大允许偏差。

记XL=X0-ΔX,XU=X0+ΔX，分别表示性能参数的允许下限和允许上限，于是根据对性能参数要求类型的不同，性能可靠性可分别表示为：

(1) 双侧允许限性能可靠性

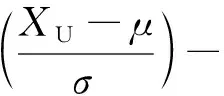
(2) 单侧允许下限性能可靠性

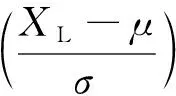
(3) 单侧允许上限性能可靠性

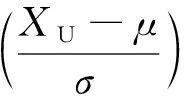
1.2 利用 Bootstrap 仿真方法估计性能参数的均值和方差

.

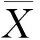
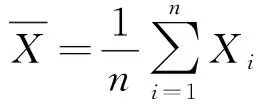
此时μ和σ2的估计误差Tn(μ)和Tn(σ2)分别为

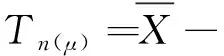
(1)

将X1,X2,…,Xn按由小到大排列，表示为：X(1)≤X(2)≤…≤X(n)，则有样本X的经验分布Fn为

.

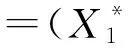
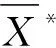
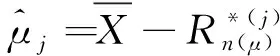
通过上述估计值可以得到μ和σ2的Bootstrap点估计值为

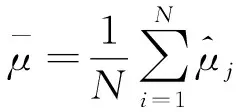
1.3 性能可靠性的评定

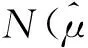
性能可靠性的置信下限[15]为

(1) 双侧允许限性能可靠性置信下限

首先由下式计算允许限系数KL与KU

由KL与KU及给定的置信度γ和样本容量n，查正态分布双侧统计允许限系数表可得到对应的概率值PL与PU，从而置信下限RL为

RL=1-(PL+PU).

(2) 单侧允许限性能可靠性置信下限

对于单侧允许下限性能可靠性，其允许限系数为

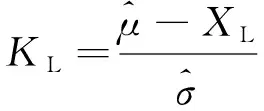
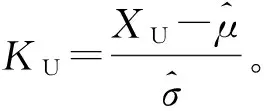
2 基于性能可靠性的鱼雷等效先验数据

通过Bayes[16]可靠性先验分布的矩法计算超参数的方式，可以将评估出的鱼雷性能可靠性转换为可靠性先验数据。由于二阶矩不易计算，因此可利用一阶矩R0与给定置信度γ下的置信下限RL进行处理，等效为成败型信息(n1，f1)。

具体地，设对应性能可靠性信息的先验分布为Beta分布：

,

则

(2)

通过式(2)求得超参数(a，b)，则等效先验数据可取：

3 综合性能可靠性的实航工作可靠度Bayes评定

当性能可靠性信息等效为成败型先验数据(n1，f1)时，对应性能可靠性信息的先验分布为Beta分布：

通过式(2)求得a，b，可取：s1=a，f1=b，n1=a+b。

令n2=s2+f2，则现场二项试验(s2,f2)发生概率为

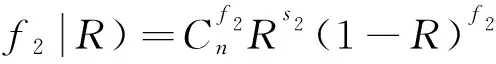
则实航工作可靠度R的后验分布由Bayes定理确定：

β(R(f1+f2,s1+s2)).

则R的点估计为

(3)

采用Bayes方法，R的置信度为γ的置信下限为

即

IRL(s1+s2,f1+f2)=1-γ.

(4)

根据Beta分布与F分布分位数间的关系：

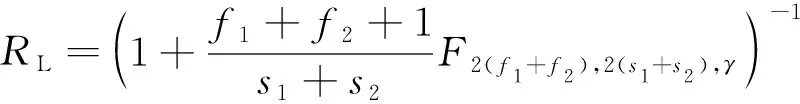
综合2节的公式及式(2)～(4)即得到了基于Bootstrap仿真方法的鱼雷实航工作可靠度小子样评定模型。

4 应用实例

某鱼雷要完成一个机械动作，根据技术要求需要在30 s内完成该动作，已知该指标对应的性能可靠性信息及现场试验信息，运用上述方法(具体流程见图1)对鱼雷实航工作可靠度进行评估(置信度γ=0.8)。

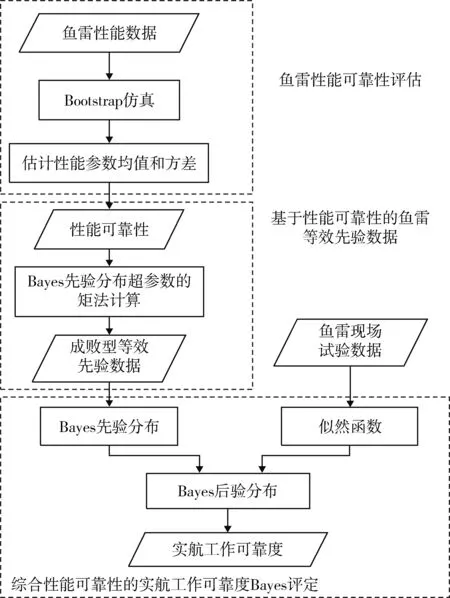
图1 评估方法流程Fig.1 Assessment method and procedure

表1所示为30个性能可靠性数据，表示鱼雷完成该机械动作所花费的时间，时间的长短意味着性

能的优劣。由于经费和时间的制约，为评估鱼雷的实航工作可靠度仅进行了4条次现场试验，结果为0条次故障，即可靠性现场试验数据为(4,0)。

表1 鱼雷某性能可靠性数据

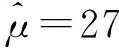
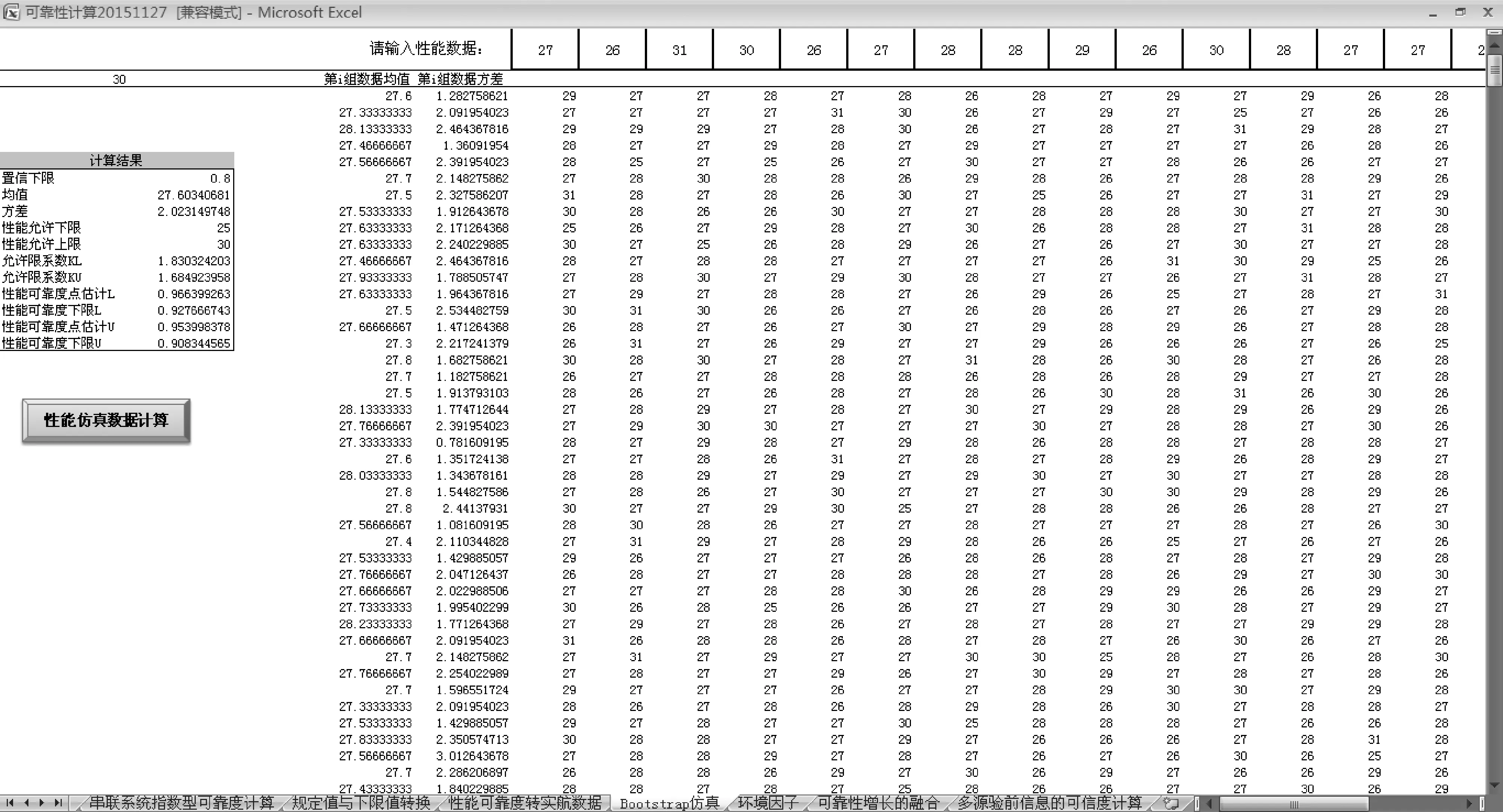
图2 仿真10 000次后性能可靠度计算界面Fig.2 Performance reliability calculation after 10 000 simulation

IRL(s1+s2,f1+f2)=1-γ.

根据Beta分布与F分布分位数间的关系

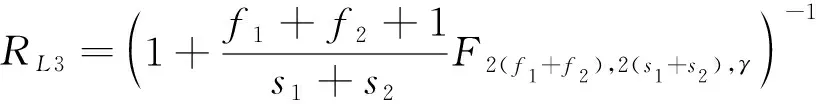
计算得点估计值和置信下限分别为R03=0.957 4，RL3=0.915 0。若不考虑鱼雷性能信息，可靠度下限评估值仅为RLA2=0.668 7。

5 结束语

本文提出的基于Bootstrap仿真方法的实航工作可靠度评定方法,充分利用Bootstrap仿真计算出的性能可靠性先验信息，采用Bayes方法综合先验信息与现场试验信息，最大限度地降低了实航工作可靠度评估样本不足对评估结果的影响,简便易行,在工程研究领域具有很好的实用价值。