高重频脉冲对被动导引头前端的干扰机理研究

南昊，彭世蕤，王晓燕，许正强

(1.空军预警学院，湖北 武汉 430019；2.空军军务信息中心，北京 100843)

0 引言

在现代战争中，以被动导引头为关键部件的反辐射武器成为雷达的主要威胁。近年来，一些新的被动导引头抗干扰技术的出现，使得对抗反辐射武器更加困难[1-5]。随着被动导引头在电磁战场上发挥的作用日益凸显，研究对其的干扰技术对提高雷达电子防御能力非常重要。

随着脉冲技术的发展，采用高重频脉冲信号对抗接收机的研究逐渐展开，文献[6]给出了高重频脉冲对雷达接收机的压制式干扰试验效果，文献[7-10]分析了高重频激光对激光导引头的干扰机理，提出干扰效果对信号重复频率有一定要求。因而高重频脉冲干扰对信号处理能力较弱的被动导引头的干扰效果更好，即使在干扰信号脉冲密度处于导引头处理能力范围内的情况下，高重频干扰同样可发挥作用。为此，本文对高重频脉冲进入导引头前端的响应情况进行理论研究，明确了高重频干扰对前端的作用机理及干扰效能与脉冲参数之间的理论关系。

1 高重频脉冲信号特征

高重频脉冲信号是一种重复频率极高的脉冲信号，脉冲宽度通常为几纳秒至几百纳秒，远小于雷达发射信号的脉冲宽度，具有超宽带的特性。其时域表达式为[11]

(1)

式中：A为脉冲幅度；τ为脉冲宽度；T为脉冲重复周期；N为脉冲数量；rect(·)为矩形函数。

将式(1)进行傅里叶变换得到高重频脉冲的频域表达式为

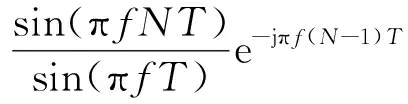
(2)

设PRFj为高重频干扰脉冲重复频率，当A=2 mV，τ=1 ns，N=1 000，PRFj=200 kHz时，高重频脉冲时域波形和频谱如图1所示。

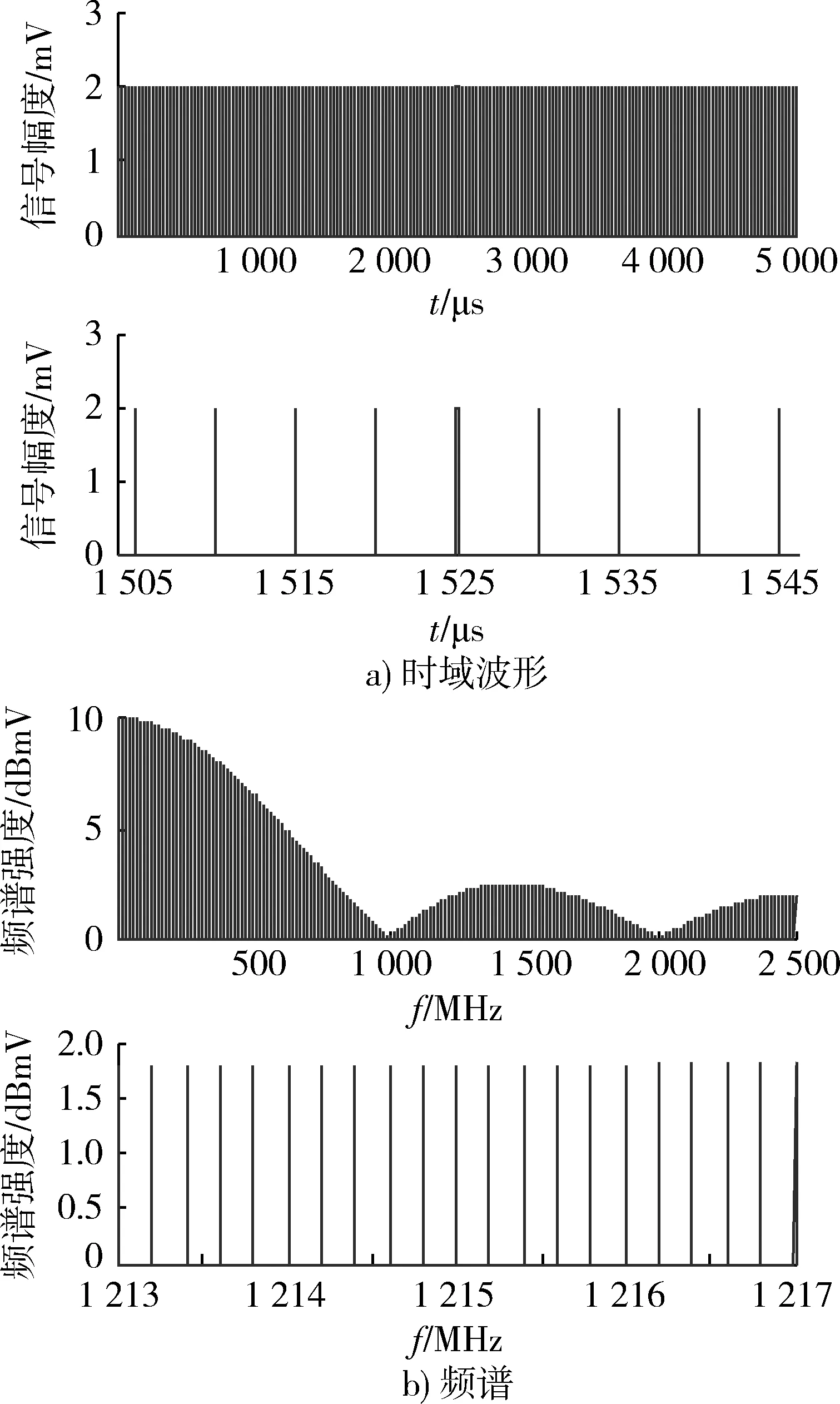
图1 高重频脉冲时域波形及频谱图Fig.1 Time-domain waveform and frequency spectrum of high PRF pulse

从图1可以看出，高重频脉冲的频谱由离散谱线组成，相邻谱线间隔为脉冲重复频率，谱线包络同sinc函数，频率覆盖范围极宽。这样，实施高重频干扰后，其宽频带特性将使干扰信号频域上能够覆盖导引头接收频带；脉冲宽度极窄使其渡越接收系统的保护电路[12]，前端模拟器件将产生严重的瞬态响应和非线性失真，最终影响信号检测。

2 干扰机理分析

被动导引头组成原理框图如图2所示。主要由限幅器、带通滤波器、低噪声放大器、混频器、中频放大器和检波器等组成，本文主要研究高重频脉冲对被动导引头前端，即限幅器、带通滤波器和低噪声放大器的影响。

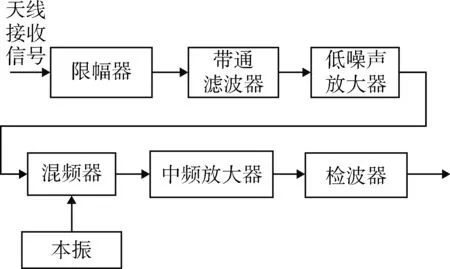
图2 被动导引头组成原理框图Fig.2 Principle block diagram of passive seeker

2.1 限幅器的瞬态响应分析

干扰脉冲从带通滤波器输出后带宽变窄、脉宽变宽、脉冲前后沿变缓，将不再产生明显的瞬态响应，因此高重频脉冲在导引头前端产生的瞬态响应主要来源于限幅器。其工作特性曲线如图3所示，低输入功率时，限幅器的输出信号幅度随输入功率增大而等比增大；当输入信号电平超过限幅器门限电平后，限幅器发挥作用使输出信号幅度增速变缓；若输入功率持续增加，限幅器内部PIN二极管将工作于饱和区，限幅器会失去作用直至器件烧毁。PIN限幅器的尖峰泄漏效应及恢复时间是造成自身工作特性受损的主要原因[13]。

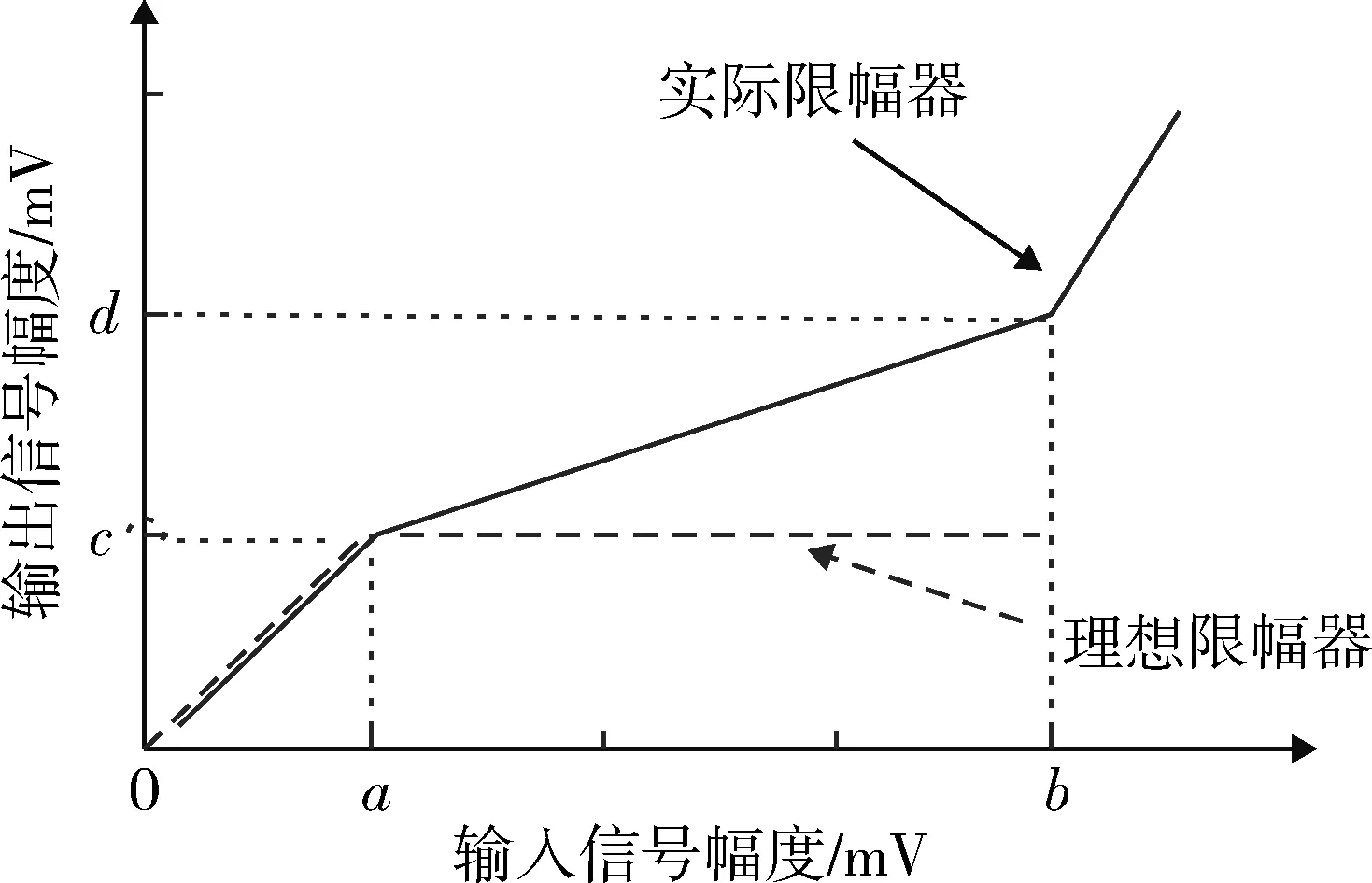
图3 限幅器工作特性曲线Fig.3 Operating characteristic curve of limiter

限幅器的响应时间通常为几十纳秒，尖峰泄漏效应是指当干扰脉冲重复频率达到MHz级甚至更高时，脉冲宽度将小于限幅器的响应时间，干扰脉冲将直接通过限幅器进入带通滤波器。当脉冲重复周期小于滤波器响应时间时，输出相邻脉冲前后沿相互叠加，会产生类噪声信号；当脉冲重复周期大于滤波器响应时间时，由于滤波器输出的干扰谱线频率与雷达信号载频非常接近，当两者频率差倒数接近雷达信号脉宽时，会产生近似噪声调幅干扰的效果，在不考虑后级电路失真影响下，检波后会压制雷达信号。

限幅器的恢复时间是高重频干扰脉冲作用的另一原因。当输入信号脉宽大于限幅器响应时间时，限幅器发挥作用。在每个输入脉冲结束后的恢复时间内，限幅器的隔离度仍然很大并将继续对输入信号进行作用，作用时间取决于恢复时间，通常为几百纳秒。此时，若干扰脉冲与雷达信号同时进入限幅器，高功率的干扰信号会降低限幅器增益，在每个干扰脉冲结束后的恢复时间内，限幅器将继续保持低增益对雷达信号作用，使雷达信号输出功率下降，影响正常检测。

这种情况下，低增益作用时间为

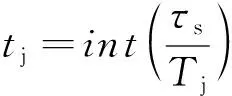
(3)

式中:int(·)表示向下取整函数;τs为雷达信号脉宽;Tj为干扰脉冲重复周期;tr为限幅器恢复时间。

对于如图3所示的限幅器工作特性曲线，其幅度增益特性可表示为

(4)

式中：Ai为输入信号幅度；Ao为输出信号幅度。

若输入雷达信号幅度为A，重复周期为Ts，脉宽为τs，则无干扰时限幅器脉冲输出平均功率为

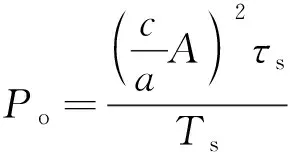
(5)

加入高重频干扰后，限幅器脉冲输出平均功率变为

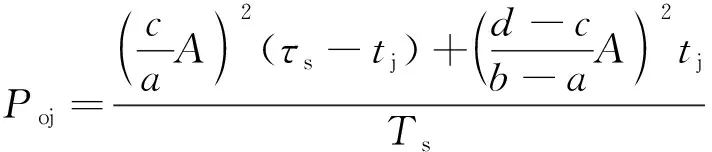
(6)

这样，脉冲输出信号功率衰减百分比为

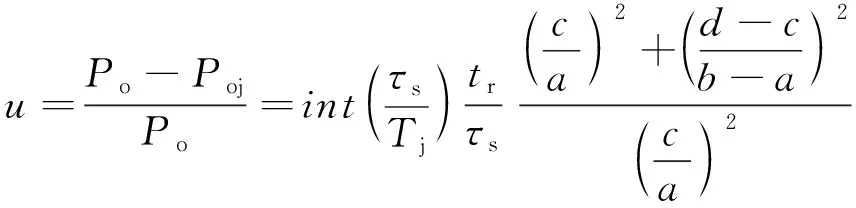
(7)

由式(7)可以看出，雷达信号脉宽、幅度一定时，干扰信号重复频率越高、限幅器恢复时间越长，输出功率衰减越大。

2.2 低噪声放大器的非线性失真分析

真实的导引头前端并非理想的线性系统。对接收到的信号进行滤波、放大等处理时，前端会因为模拟器件的非线性特性产生失真，且失真产物功率的增加会降低导引头前端输出信干比，影响信号检测。

前端的非线性失真主要来源于低噪声放大器，其工作特性分为线性和非线性2种。在线性状态下，放大器输出信号的功率随着输入信号功率的增加而等比增加；当输入功率增大到某特定值时，进入非线性状态，输出信号功率不再等比增大。由于高重频脉冲具有超宽带特性，包含较多频率分量，必定会产生多种非线性失真产物，增加干扰功率进而影响后续信号检测。其中，三阶互调产物是奇数阶互调分量里频率最接近雷达信号且能量最强的失真产物，它是在非线性状态下由雷达信号的二次谐波与干扰信号混频产生的[14]。为保证对信号的侦收，接收机带宽不能过窄，因此干扰信号很难被滤除。

2.3 压制效果的评估

假设带通滤波器为理想滤波器且中心频率对准雷达信号，干扰脉冲进入混频器和中放后不会产生失真。当限幅器响应时间大于干扰脉冲宽度，干扰脉冲将直接渡越限幅器压制雷达信号，为评估干扰效果，分析前端输出信干比。

导引头前端接收到的雷达信号功率Psr和干扰信号功率Pjr为

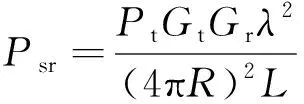
(8)

(9)

式中:Pt,Ptj,Gt,Gtj分别为雷达和干扰源的发射功率及增益;R,Rj为雷达、干扰源与导引头(看作质点)的距离;Gr为导引头天线增益;λ为雷达信号波长;L为信号传播过程中考虑馈线、极化和大气衰减后的总损耗，通常为15～17 dB。

设带通滤波器带宽为B，通常情况下B远小于干扰信号频谱宽度，此时认为所有进入滤波器的干扰谱线强度近似相等，均为滤波器中心频率对应谱线的强度。这样，直接落入接收频带的干扰功率为

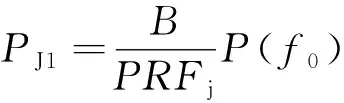
(10)

式中:PRFj为干扰脉冲重复频率;f0为带通滤波器中心频率;P(f0)为滤波器中心频率对应干扰谱线的功率，大小为

(11)

式中:JB(f)为通过滤波器的频率为f的干扰谱线强度，大小为

JB(f)=H(f)J(f),

(12)

H(f)为带通滤波器传输特性，理想情况下有

(13)

式中:fL，fH为滤波器的起始频率和截止频率。

根据三阶互调功率的计算方法[15]，干扰脉冲进入放大器后产生的三阶互调失真功率为

PJ2=3(PJ1+G)-2Q3,

(14)

式中:G为放大器增益;Q3为放大器三阶截交点，通常在放大器的技术指标中给定。

而接收机噪声功率大小为

PNo=kT0FB,

(15)

式中:k为玻尔兹曼常数;T0为接收机温度;F为噪声系数。

这样，导引头前端输出的干扰功率由直接落入接收机通频带的干扰功率和放大器三阶互调失真功率组成。前端输出信干比为

(16)

3 仿真验证

由于前端输出信干比是随着被动导引头空间位置的变化而实时变化的，为便于分析，在某一时刻将雷达、干扰源和导引头的位置固定，并以雷达为原点，建立空间直角坐标系。仿真中设定的导引头和干扰源坐标为(-4 000,-3 210,0) m,(-3 000,-3 000,3 000) m。雷达参数如下：载频f0=1 215 MHz，τs=1.12 μs，Gt=40 dB。导引头各器件参数如下：接收天线增益Gr=3 dB；放大器Q3=18 dBmW，G=18 dB；带通滤波器参数：fL=645 MHz，fH=655 MHz，k=1.38e-23，T0=290 K，F=12 dB，信号传输过程中总损耗L=17 dB。

3.1 限幅器瞬态响应仿真及分析

设限幅器响应时间tx=10 ns，a=c=0.5 mV,b=5 mV,d=1 mV，干扰信号脉宽τj=1 ns。此时限幅器产生尖峰泄漏效应，设滤波器响应时间为0.1 μs。当Pt=500 W，PRFj=50 MHz，Gtj=40 dB，Ptj=50 kW时，带通滤波器输出干扰脉冲波形如图4a)所示，干扰前后检波输出波形如图4b)所示。

从图4可以看出，干扰脉冲重复频率为50MHz时，由于脉冲重复周期小于滤波器响应时间，干扰信号滤波后前后沿脉冲叠加，检波后将雷达信号完全压制，已无法完成正常检测。PRFj=0.5 MHz，Ptj=5 MW，其余参数不变，仿真结果如图5所示。

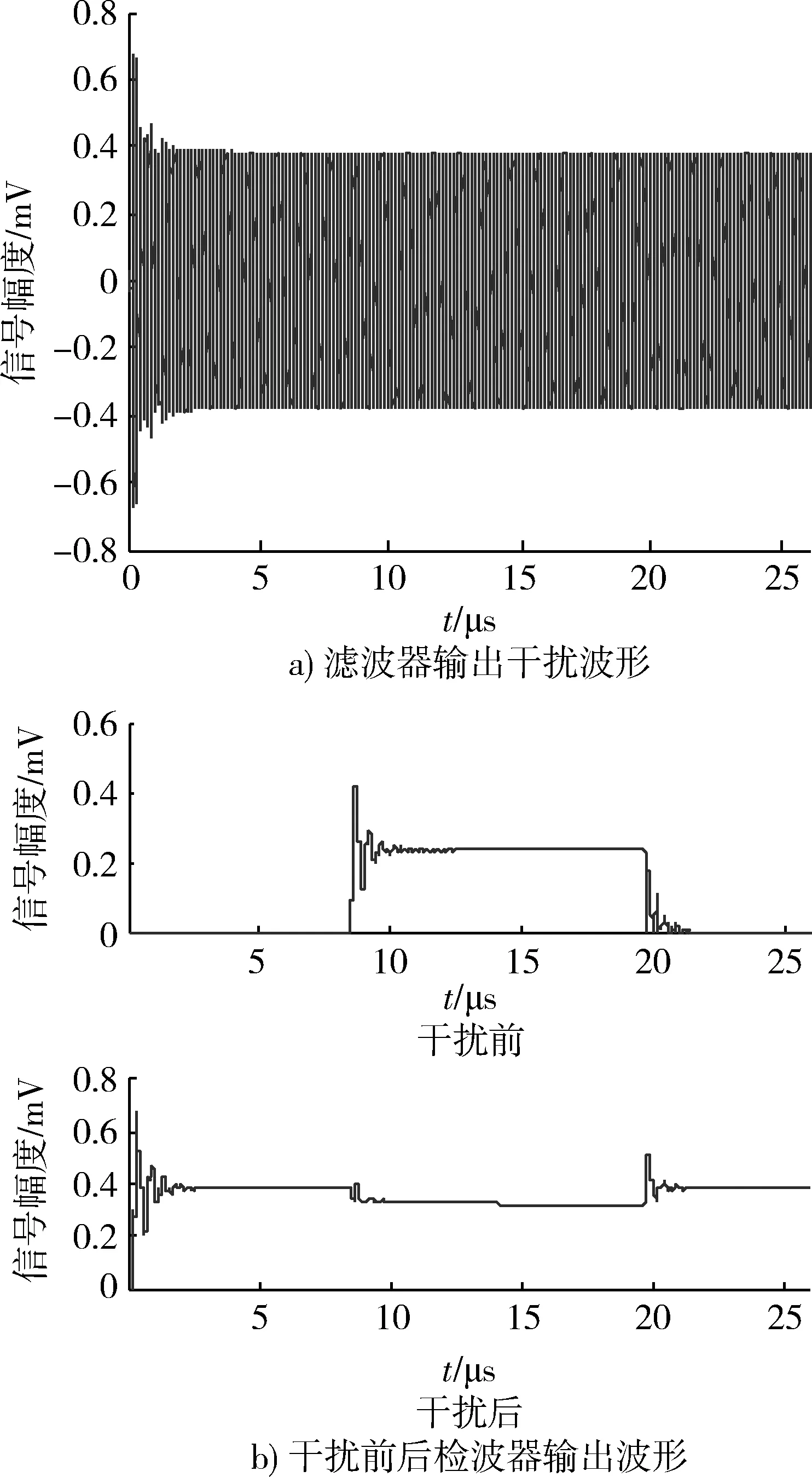
图4 压制干扰仿真结果(重频为50 MHz)Fig.4 Simulation results of suppressive interference(PRFj=50 MHz)

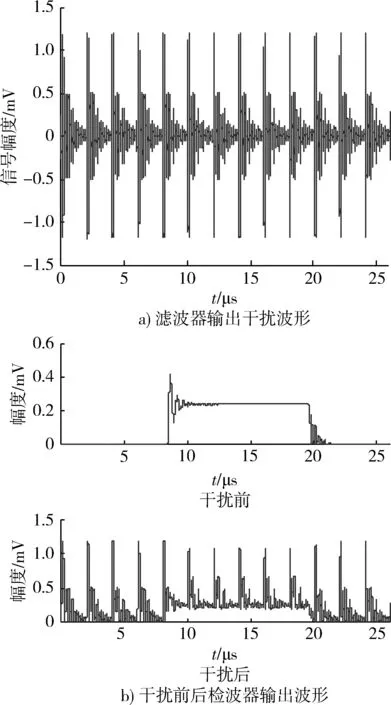
图5 压制干扰仿真结果(重频为0.5 MHz)Fig.5 Simulation results of suppressive interference(PRFj=0.5 MHz)

从图5可以看出，干扰脉冲重复频率为0.5 MHz时，脉冲重复周期大于滤波器响应时间，干扰脉冲经过滤波器后相邻脉冲没有叠加，但由于噪声调幅干扰起遮盖作用的主要是旁频成分，干扰功率足够大时同样压制了雷达信号。

设限幅器响应时间tx分别选为100,150和200 ns。高重频脉冲参数：Pt=500 W，τj=40 ns，PRFj分别选为50,100,150,200,250 kHz。根据式(7)进行计算，结果如表1所示。

从表1可以看出，当τj>tx时，无尖峰泄漏效应产生。但高重频干扰使限幅器工作特性改变，在恢复时间内导致信号输出功率衰减。干扰重复频率越高、限幅器恢复时间越长，衰减百分比越大，验证了理论分析。对于不同的恢复时间，当干扰脉冲重复频率从50 kHz增加到250 kHz时，输出信号功率衰减百分比均小于2%，最大值为1.87%。此时，可以忽略恢复时间导致的信号功率衰减，说明尖峰泄漏效应是高重频脉冲对前端干扰奏效的主要原因。

表1 输出信号功率衰减百分比

3.2 干扰脉冲参数对信干比的影响

当Gtj=40 dB,PRFj=100 kHz时，分别改变干扰功率及脉宽，根据式(16)进行仿真，得到前端输出信干比变化情况如图6所示。

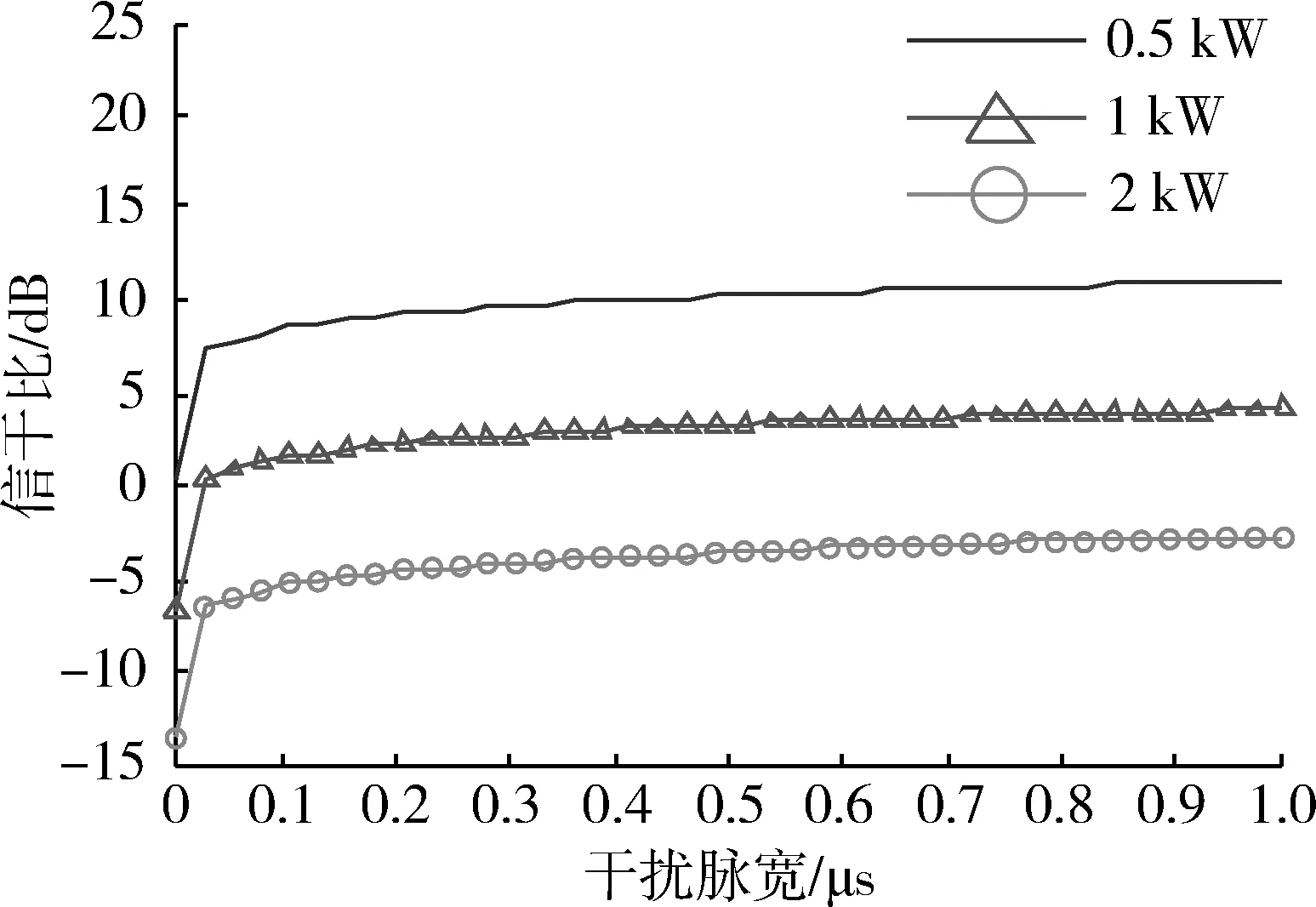
图6 信干比随干扰脉宽变化曲线Fig.6 SJR with the variation of jamming pulse width

从图6可以看出，干扰脉宽一定时，干扰功率越大，前端输出信干比越低；干扰功率一定时，干扰脉宽越宽，输出信干比越高。这是由于在脉宽一定时，干扰功率增大必然会导致信干比降低；干扰脉宽增加后，频谱包络发生改变，通过带通滤波器2进入后级的干扰能量占总能量的比重减小，使干扰功率减小，导致信干比降低。当脉冲宽度为1 ns，脉冲重复频率为100 kHz，干扰功率达到约500 W时，信干比降至0。当Ptj=1 kW时，改变脉冲重复频率得到前端输出信干比变化情况如图7所示。

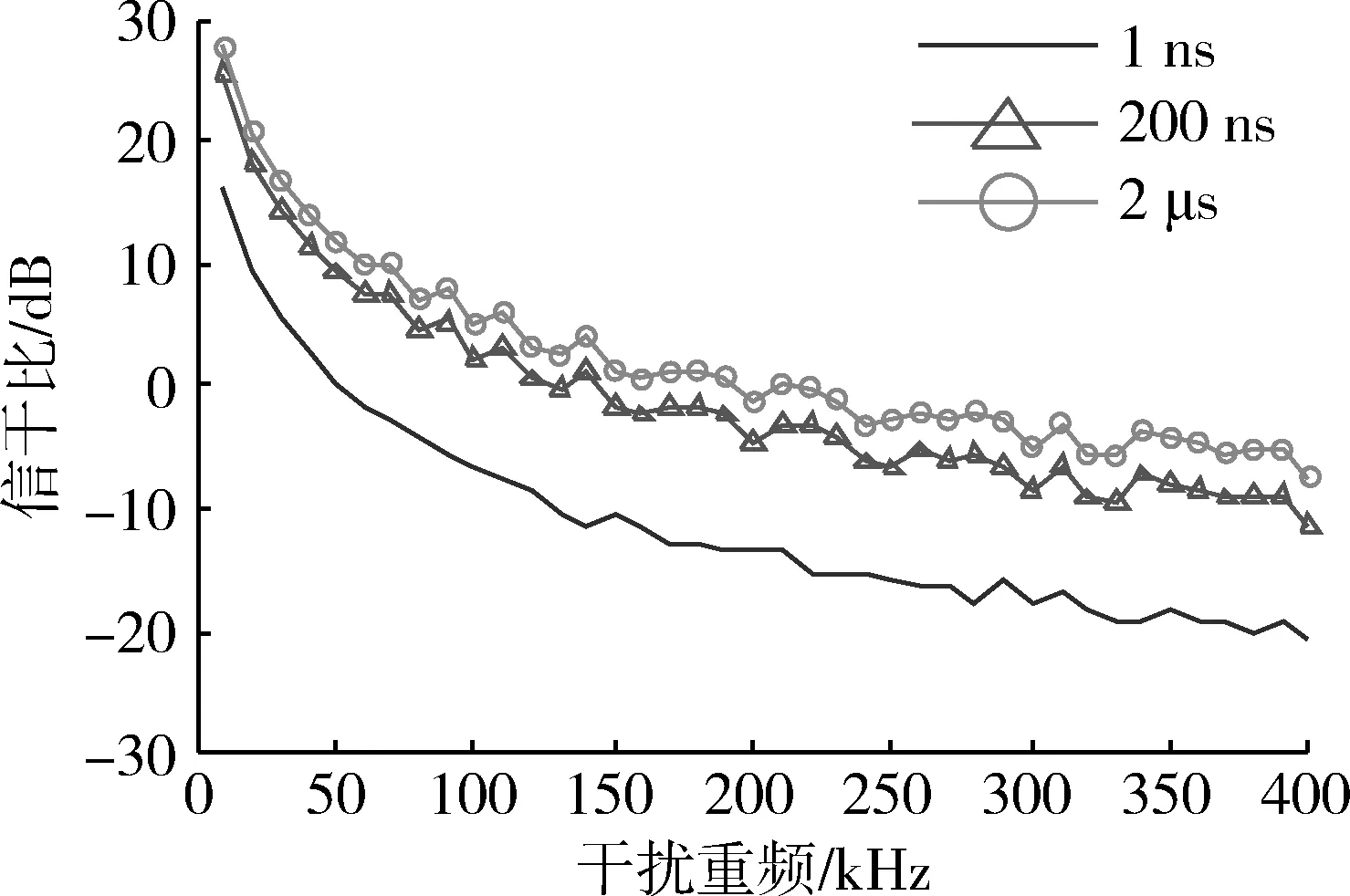
图7 信干比随干扰重频变化曲线Fig.7 SJR with the variation of jamming PRF

从图7可以看出，干扰脉冲宽度一定时，脉冲重复频率增大，前端输出信干比降低。这是由于干扰机发射峰值功率一定时，虽然通过滤波器进入后级的干扰能量占总能量的比重无变化，但是脉冲重复频率越高，导引头前端接收到的平均功率将增大，使前端输出信干比降低。当脉冲重复频率约50 kHz时，输出信干比降至0。

4 结束语

本文研究了高重频脉冲在导引头前端的作用机理，仿真验证了分析结果，得到了脉冲参数与干扰效果之间的理论关系。结果表明，当干扰信号脉宽小于限幅器响应时间时，尖峰泄漏效应导致干扰脉冲直接进入后续处理电路，检波后对雷达信号形成压制；限幅器恢复时间造成的输出功率衰减不是高重频干扰作用的主要原因；干扰功率越大，脉冲宽度越小，脉冲重复频率越高时，前端输出信干比越低。上述结论是在雷达、干扰机和被动导引头相对位置固定的条件下得到的，在实际运用中必须充分考虑导引头的工作模式和运动轨迹，合理布设干扰机并调整高重频脉冲参数，使干扰效果达到最佳。