基于PNN的变压器故障诊断模型研究
2018-10-27勒国庆
勒国庆,王 浩
(邵阳学院 多电源地区电网运行与控制湖南省重点实验室,湖南 邵阳,422000)
通过研究变压器的故障诊断方法,并针对当前故障诊断中存在的重点问题,在智能算法的改进、实现和方法融合等方面做出了研究,其中主要研究的人工智能算法是PNN算法。
1989年,D.F.Specht博士最先提出PNN,这是一种并行算法,它源自于Bayes分类规则与Parzen窗的概率密度函数估计方法,并经过长期的发展而得来的[1]。PNN是一种具有强大的非线性分类能力的算法,它能较为准确地把样本空间反映到故障模式空间,使得最终的数据误差在允许范围内,并具有较强的自适应结构能力,较之前的Bayes神经网络相比不易陷入局部最优解。通过分析Matlab仿真结果,得出其可以有效提高变压器故障诊断的准确性[2-5]。
1 变压器的常见故障及诊断方法
1.1 变压器的常见故障
变压器故障分类方法因分类标准而异。在研究变压器的故障类型时,主要是按照故障的性质分类的,主要包含5种故障类型,分别是中低温过热、高温过热、局部放电、低能放电以及高能放电[6]。表1是国家电网对359台故障变压器的故障类型统计。

表1 变压器故障类型统计
1.2 变压器故障诊断
三比值法是变压器故障诊断的最基本方法,也是能够最广泛用于实践的一种方法,其工作原理是:变压器内部发生故障时会产生气体,根据各种气体的相对比值在不同时间的变化,从而确定变压器的运行状态。本次研究在进行编码时,选用的是5种特征气体,分别为甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)和氢气(H2),从而构成三对比值,分别为C2H2/C2H4、CH4/H2、C2H4/C2H6,然后根据各个比值的范围,编写不同的代码[7]。首先将计算出每组气体的比值,通过查找表中数据得到每组气体所对应的编码,然后把这三组气体对应的编码合并组合起来,最后对照编码组合表,从中找出其对应的变压器基本故障类型。
通过上述分析可以发现:测量后编码并对三种气体的比值进行对比分析,仍然需要很大的人力和物力,故结合人工智能的变压器故障诊断方法为变压器的故障诊断开辟了新的途径。在人工智能领域中,人工神经网络和专家系统的研究最为突出,所以文中主要对概率神经网络展开研究分析。
2 模型建立
将油中溶解气体三比值数据作为神经网络的输入特征向量,将5种变压器故障类型作为输出特征向量并在模型输出层输出,还可以通过实际的生产生活需要对诊断的故障类型数进行扩展,前提是要采集到足够多种类的样本集[8]。
采用Matlab对基于PNN的变压器故障诊断模型进行仿真整体设计流程框图如图1所示。

图1 基于PNN的变压器故障诊断模型整体设计框图Fig.1 Overall design block diagram of transformer fault diagnosis model based on PNN
故障诊断模型建立成功后,用上文提到的Matlab调用PNN函数来进行仿真。神经网络的结构和Matlab库中函数有如下对应:第一层是输入层,它属于径向基层,该层使用函数netprod计算,第二层是模式层,它是一种竞争模式的网络层,由dotprod函数来计算其所占的权重[1]。模型当中使用函数netsum计算网络输入。只有newpnn的第一层才具有阈值向量,在设置的时候把第一层设置为输入向量的转置P′,并且将所有阈值向量设置为0.8326/spread,故在加权输入向量中,径向基函数设置+/-spread值为0.5,第二层权值向量为目标向量T[9]。PNN是一种径向基网络,并且十分适用于模式分类领域,在设置分类时,其spread接近于0时构成最近的邻近分类器,当spread值较大时可以形成对多个训练样本的邻近分类器。
3 PNN变压器故障诊断的仿真结果分析
文中研究的基于PNN的故障诊断系统中,训练样本数和扩散值spread都会影响到诊断结果的准确性[10]。本研究需要确定两者对PNN诊断性能有何具体影响,因此下面将展开如下的验证操作:首先通过实验探究故障样本数目的大小对诊断准确率的影响。为此,从所有搜集到的样本数据中选取4组样本数进行网络训练,选取的样本数分别为:15,25,35,45。为了能够准确检测样本数量对PNN网络的诊断准确率的影响,spread值全部取0.2,并使用15个样本来对其验证。
在Matlab的仿真环境当中可以直接通过newpnn()来调用pnn模块。在仿真中输入pnn4515.data,它是60x4维的矩阵,前三列代表不同的三种气体的比值,矩阵的最后一列表示变压器运行的实际故障类型,60行则代表的是样本集为60个。
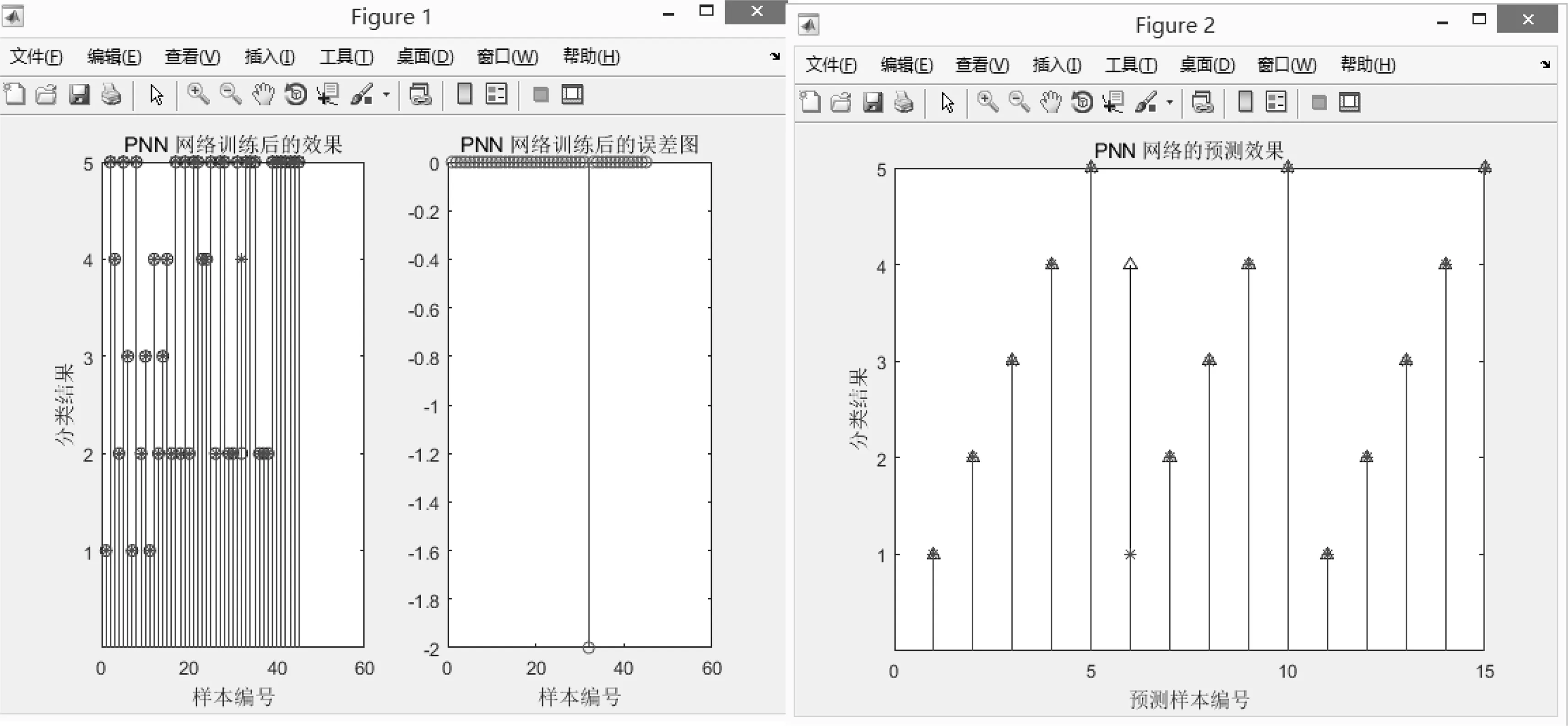
当训练样本数量为45时,根据图2可以看出通过Matlab的figure绘图函数调用之后,“筷”状图的顶点有“*”和“^”两种图形表示方式。其中“筷”状图顶点画“*”的代表的是“t_train_temp”,即真实的样本值,其对应的纵坐标为样本的真实故障类型。顶点为“^”的代表“p_test”,即PNN网络的变压器故障分类预测值。
图2是训练样本为45的PNN训练与预测结果图,样本3,4,8,11,13的“筷”状图顶点“*”和“^”都没有发生重合,这5个样本在训练样本数为35的训练环境下诊断预测出现失误。

图2 训练样本为45诊断结果图 Fig.2 Diagnostic result of training sample 45
训练样本数量不同,诊断所得出的结果也不同,相应的诊断的准确率也不同,对诊断结果进行统计与分析的结果详见表2所示。

表2 基于PNN训练样本数不同情况下对应的检测结果汇总表

续表
注:表中带*号的为诊断与实际故障类型产生偏差的样本,1-5所代表的故障类型依旧为:1代表正常状态;2代表低能放电;3代表高能放电;4代表中低温过热;5代表高温过热。
对表2中基于PNN训练样本数不同情况下对应的检测结果汇总表进行分类统计,可以得到不同训练样本数目分别对应的检测正确概率值,汇总后如表3所示。

表3 基于PNN训练样本数不同情况下对应的检测正确率
由表2和表3可以得出如下结论:预测诊断的正确率和训练样本的个数是成正比的,即能够采集到足够多的变压器油中溶解气体比值的样本数据,并对PNN网络进行训练,则故障诊断的准确度会提升。另外,通过Matlab仿真结果可以发现,样本数据的质量可以影响到故障诊断的准确性,所以选取的样本不但要具有典型性,还必须有一定的覆盖率,还要能够基本涵盖所需要检测的故障类型样本。
而后,把Spread值以递增形式分别取0.1,0.2,0.4,0.6,0.8,1.0,其他条件如训练样本数和检测样本数都相同的情况下来进行Matlab仿真研究。将训练样本集和检测样本集建立一个mat文件做好存储,将其命名为“pnn.mat”。在Matlab进行仿真研究过程当中,均采用15组数据作为检测样本集进行检测,由于数据繁琐,所以直接在表4直接汇总展示。

表4 spread值对于诊断率的影响
从表4可以看出,spread值将直接影响诊断的精确度,且当spread值为0.1时,系统的故障诊断准确率最高,准确率达到73.3%。但对于各个生产生活领域对变压器故障诊断准确率的需求来说,这还是远远不够的,因此为了提高诊断精度,在下面将对基于PNN的变压器故障诊断模型加上RS粗糙集理论进行改进。
4 RS-PNN相结合的变压器故障诊断
4.1 RS与PNN结合的变压器故障诊断
RS和PNN用于诊断变压器故障。把RS理论作为PNN网络第一层输入层结构的前置环节,使用RS对大量的样本集进行简约和优化,因为RS理论不在乎样本数据集的分布,而且在获取样本数据信息不全面的境地下,也不会对RS理论产生影响,具有很强的适应性,不需要主观地评估知识和数据,更不需要对先前的知识进行足够量的积累[11]。因此通过使用RS理论,在输入层对即将输入之前进行数据预处理。具体诊断模型如图3所示。

图3 RS-PNN诊断模型Fig.3 RS-PNN diagnostic model
下面以一组数据来具体说明RS粗糙集理论是如何处理样本输入信息的(输入分别为X1,X2,X3):
通过这样一组公式有:
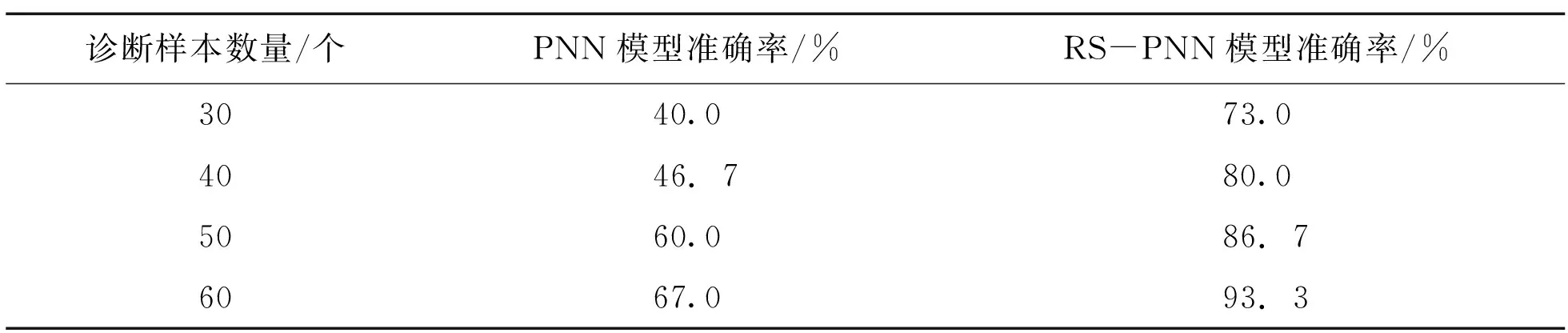
1)当0≤X1<0.1时,有I1取0.5;当0.1≤X1<1时,有I1取1;当1 2)当0≤X2≤1时,有I2取0;当0.1≤X2<3时,有I2=1-e(-x2-0.1)2;当3≤X2时,I2取1; 3)当0≤X3≤0.1时,I3取0;当1≤X3<3时,有I3=1-e-0.5(x3-0.1)2;当3≤X3时,I3取1; 这样一来原本的样本输入集就变成了I1=0,I2=1,I3=0。 神经网络的输入特征矢量选取IEC(改良后的三比值法),分别为:CH4/H2,C2H2/C2H4,C2H4/C2H6;输出故障类型选为5种,分别为:1.正常;2.低能放电;3.高能放电;4.中低温过热;5.高温过热[4]。 将RS粗糙集理论优化后的样本数据作为新的输入量,保持样本数据的数量与前面基于PNN的变压器故障诊断样本数据个数不变,Spread值仍然保持为0.2,可以得到下面的预测诊断结果。 将样本为60的故障数据先通过RS粗糙集理论进行处理后,再作为PNN诊断模型的输入变量,通过图4可以看出,在增大训练样本集合RS理论的双重作用下,15个诊断数据样本中仅样本6发生了预测错误,较40个样本集的准确率又有了进一步的提升。 图4 RS-PNN网络的预测效果图(样本为60)Fig.4 RS-PNN network prediction effect diagram(sample number is 60) 将相同变压器运行状态下的数据样本在通过PNN变压器故障诊断模型处理后得到的输出预测结果与通过RS粗糙集处理过后的RS-PNN模型处理预测结果汇总,如表5所示。 表5 基于RS-PNN不同训练样本数对应的检测结果汇总表 续表 注:表中带*号的为诊断与实际故障类型产生偏差的样本,1-5所代表的故障类型依旧为:1代表正常状态;2代表低能放电;3代表高能放电;4代表中低温过热;5代表高温过热。 对表5中基于RS-PNN不同训练样本数对应的检测结果汇总表进行分类统计,可以得到在RS-PNN网络模型中不同训练样本数目分别对应的检测正确概率值,汇总后如表6所示。 表6 基于RS-PNN训练样本数不同情况下对应的检测正确率 由以上内容可以知道,基于RS优化的PNN故障诊断模型的诊断精确度比未经过优化的PNN网络诊断的高,在诊断中引入RS粗糙集理论可以适量的去处冗余,简化系统,并且提升诊断精确度。 下面列一表格来将相同样本数量下,基于PNN的变压器故障诊断模型诊断的结果和诊断准确率与基于RS-PNN的变压器故障诊断结果做对比,如表7所示。 表7 RS改进前后的诊断模型对比 通过表7将PNN网络诊断结果的判定结果对比分析RS优化的PNN模型的诊断精确度最高,可达93.3%,而且该诊断模型的反应速度也快,经过对比证明,PNN网络诊断更适合运用于变压器故障诊断中。 通过对基于PNN的变压故障诊断模型进行了仿真研究,得出的结论是选取样本集的大小、质量以及Spread值的大小都可以对诊断的准确率产生一定的影响。除此之外,本次研究还通过RS对PNN诊断模型进行了优化,取得了一定的成果。但要想进一步改进神经网络诊断模型,仍然需要进一步探讨改进。 1)欲实现变压器能够在线进行故障诊断,如何进行收集溶解气体数据的比值样本,如何实现样本数据的传输和转换,要对此进行更深的考虑。 2)当下使用DGA的各种变压器故障诊断技术的最大缺点,是它不能确定故障位置,因此,将气体发生率与实验结合,利用超声波定位技术来实现变压器的故障诊断将拥有较好的研究潜力。4.2 RS-PNN网络诊断结果的判定
4.3 RS-PNN仿真结果分析



4.4 对比与分析
5 总结与展望
