一类新的非线性发展包含问题
2018-10-27刘小佑
刘小佑,代 帆
(南华大学 数理学院,湖南 衡阳,421001)
最近,在文献[1-3]中讨论了几类带历史依赖(history-dependent)项的变分-半变分不等式解的存在性及其在接触力学中的应用。在这些文献中,由于多值项是由Clarke次微分[4]定义的,可知这些多值项是取凸值的。在文中,将把上述问题推广到多值项允许取非凸值的非线性发展包含的情形。众所周知,非线性发展包含[1-3,5-9]具有很广泛的应用。
记I=[0,T],T>0为常数。设(V,H,V*)为一个三重发展包含(evolution triples of spaces)。考虑如下一类抽象的非线性发展包含问题:
(1)
其中A:I×V→V*是一个非线性单调算子,δ为一个适当定义的,用来模拟历史依赖项的非线性算子(此处的δu(t)≜(δu)(t)),F:I×H→2H{Φ}是一个可能取非凸值的集值函数,u0∈V为方程给定的初值,此处关于时间的导数是向量值分布(vectorial distributions)意义下的。在下文中将讨论上述非线性发展包含问题(1)弱解的存在性。
1 预备知识
在此小节将介绍一些以后要用到的预备知识。
称(V,H,V*)为一个三重发展包含,若V是一个可分自反的Banach空间,H是一个可分的Hilbert空间,嵌入V⊆H是连续和稠密的。V*表示V的对偶空间。
设2≤p<+。引入以下空间,其中1/p+1/q=1。记空间此处的时间导数同上也是向量值分布意义下的。空间W赋予范数后,它成为一个可分自反的Banach空间[6]。此时有以下连续嵌入W⊆⊆⊆和W⊆C(I,H)。另外若嵌入V⊆H还是紧的,则W紧嵌入到用w~V表示给空间V赋予的是弱拓扑。如无特别说明,空间V都是指强拓扑(范数拓扑)。
设Y和H为两个可分的Banach空间。集值函数F:I→2Y称为是可测的(弱可测的),若对任意闭集(开集)E⊆Y,集合{t∈I:F(t)∩E≠Φ}是可测的。相应地,若集值函数为F:I×H→2Y,其可测性的定义是相对于I×H中的σ代数Σ×B,此B表示空间H中的Borel集σ代数[10]。设X和Z是两个Hausdorff拓扑空间。集值函数F:X→2Z{Φ}称为在点x0∈X是下半连续的(简记为l.s.c.),若对任意开集O⊆Z,F(x0)∩O≠Φ,则存在点x0的邻域U(x0),使得对任意x∈U(x0)有F(x)∩O≠Φ。有关更多集值分析的内容请参看文献[11]。集值函数F:I→2Y所有属于Lp(I,Y)(1≤p≤+)的可测选择记为即有

下面给出考虑问题(1)所需要的假设条件。
H(A)算子A:I×V→V*满足:
1)∀v∈V,t→A(t,v)是可测的;
2)对a.e.t∈I,v→A(t,v)是单调的和半连续的(hemicontinuous);
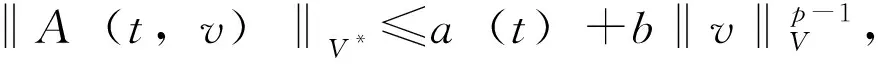
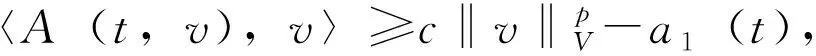
H(F)集值函数F:I×H→2H{Φ}是取闭值的,且满足:
1)对a.e.t∈I,h→F(t,h)是下半连续的;
2)映射(t,h)→F(t,h)是弱可测的;
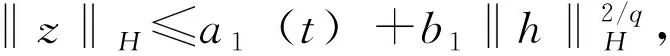

其中R:I×H→H满足:
1)t→R(t,h)是可测的;
2)h→R(t,h)是连续的;
2 相关引理
首先给出问题(1)的解的一个先验估计。
引理1 若假设H(A),H(δ)和H(F)满足,则存在常数L>0,使得对问题(1)的任一可能解u都有
江西省的网络教研平台早已经建立,它的目标是在全国实现最优的教研平台。通过该平台以及江西省网络教育资源的多方扶持,从而将信息技术对教师开展教学活动的优势得到最大限度发挥,为教师开展高效的网络教研提供支持,使教师的教学能力不断提升,从而实现教育的均衡发展。系统采用了成熟的平台技术,系统设计采用了“平台+应用”的思想进行建构,从而使得系统具有高效性与灵活性。例如在教师的教研环节,可以设立评比板块,展示教师的教研成果,从而激发教师对于网络空间建设的积极性。
‖u‖W≤L,‖u‖C(I,H)≤L
(2)
引理1的证明过程是相对容易的,故在此略去。可以参看文献[7-8]中类似估计的证明过程。记ψ(t)=d(t)+a1(t)+b1L2/q+e(TLp)2(p-1),显然ψ∈Lq(I,R+)。引入集合
(3)

为求解问题(1),先考虑以下辅助算子方程:
(4)
上述辅助问题的解算子记为u=S(g)。
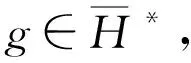
3 存在性证明
定理1 若假设H(A),H(δ)和H(F)满足,则问题(1)至少存在一个解。

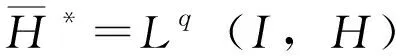
下面将证明u→G(u)是下半连续的。设u*∈C(I,H),g*∈G(u*)和在空间C(I,H)中,un→u*。由集值函数G的定义,不妨设g*=δu*+f*,其中f*(t)∈F(t,u*(t))。由文献[13]中引理3.2,存在fn(t)∈F(t,un(t))使
‖g*(t)-gn(t)‖H≤
‖δu*(t)-δun(t)‖H+‖f*(t)-fn(t)‖H≤
‖δu*(t)-δun(t)‖H+dH(f*(t),F(t,un(t)))+1/n
(5)
对a.e.t∈I成立,其中gn=δun+fn。由于集值函数h→F(t,h)是下半连续的,由文献[11]可知,函数u→dH(f*(t),F(t,u))是上半连续的。因此由式(5)和δ算子的连续性(注意到在空间C(I,H)中,un→u*)可知,必要时可取子列,对a.e.t∈I有,
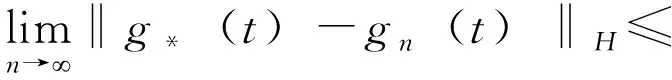
m(u)∈G(u),∀u∈Δ。

4 结语
文中研究了一类具有历史依赖项的非线性发展包含问题,它是最近一些文献中相应问题的推广。在这里最主要的创新点是允许多值项取非凸值(而非已有文献中的只取凸值),并且非线性算子v→A(t,v)只要求单调就行,而非文献中的严格单调。在适当的条件下,得到了发展包含问题解的存在性。
