基于改进的多块核主元分析的 风电机组故障诊断方法
2018-10-26贾子文顾煜炯
贾子文, 顾煜炯
(华北电力大学 能源动力与机械工程学院, 北京 102206)
风电机组的安全稳定高效运行是风力发电行业的基本要求。但是风电场选址大多在偏远地区,恶劣的环境和非稳定负荷变化等因素对机组的正常运行带来较大影响[1]。随着风电机组运行时间的增加,其维护费用呈逐年上升的趋势。当机组服役时间超过20年时,其维护成本占能源成本的15%左右[2]。风力发电行业前期投入大,资本回笼慢,过高的运维开销是风电行业发展的重大隐患。因此,对风电机组设备运行状态进行实时监测、及时准确诊断机组故障是避免严重故障发生和降低事后维修费用的有效途径。
风电机组作为大型户外发电设备,风速、温度、雨水和沙尘等自然因素均会对机组运行状态造成影响。运行工况的时变性增大了诊断风电机组故障的难度。在既定工况下通过单纯的数据特征分析已不能满足风电机组故障诊断的要求[3]。卢锦玲等[4]对极限学习机方法进行改进,将风电机组主轴轴承振动信号作为模型输入,研究了主轴轴承的故障诊断问题。Kusiak等[5]根据实时风速对机组运行工况进行划分,确定了监测各个工况振动数据的阈值。向玲等[6]将小波包与固有时间尺度分解方法相结合,通过振动信号主要特征分量的关联维数计算实现了风电机组齿轮箱的故障诊断。但以上研究大多仅对机组某一类型的运行参数进行分析,单一数据特征有时并不能充分反映机组运行工况的时变性与多样性。李静立等[7]将模态参数识别与阶次分析应用到风电机组齿轮箱状态监测领域,完成了在动态环境下齿轮箱运行状态的识别工作。Zhang等[8]和王雅琳等[9]采用多块核主元分析(MBKPCA)方法对运行数据进行分块处理,实现了设备故障发生位置的诊断。但是以上研究对于运行数据划分的主观性过强,缺乏对变量之间关联性的分析。郭鹏等[10]采用非线性状态估计方法对风电机组齿轮箱油温趋势进行分析,提高了齿轮箱诊断结果的精度,虽然考虑了机组在确定工况下运行过程的组成,但是在进行样本数据遴选过程中没有形成样本数据与运行过程的对应关系,对数据特征没有进行明确说明。
针对以上问题,笔者提出一种基于因子分析改进的MBKPCA方法,可实现风电机组的状态监测与诊断。采用对应分析方法对风电机组的样本数据与变量进行关联性分析,确定机组在正常状态下各运行过程对变量的影响程度,明确数据分块份数及每个子块的实际意义,可提高各子块分析结果的解释能力;采用因子分析方法,通过对机组各运行状态下数据特征贡献率的计算,确定正常情况下的典型数据并作为最终诊断模型的样本,提高MBKPCA方法的准确性。
1 MBKPCA方法及改进
1.1 KPCA与MBKPCA方法
核主元分析法(KPCA)[11]是在传统主元分析法(PCA)基础上引入核函数概念的方法,通过非线性函数将输入的低维数据映射到高维空间中进行处理,用核函数运算代替非线性变换后进行特征空间内积运算,可减少计算量。假设X={X1,X2,…,Xn}作为KPCA的变量输入序列,其中每个变量有m个样本。考虑到机组运行数据的非线性特点,采用非线性映射Φ:RM→F,将原始输入数据在高维特征空间中展开。其中,特征空间F的协方差矩阵为:
(1)
式中:n为参与分析的变量序列长度。

(2)
式中:αi为核矩阵K的特征向量中第i个值。
引入核函数Kjk=K(Xj,Xk)=Φ(Xj)Φ(Xk),表示核矩阵K中第j行、第k列的值,K的特征值可表示为:
λα=(1/n)Kα
(3)

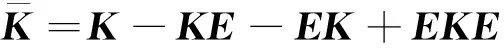
(4)
式中:E为单位矩阵。
通过主元分析中的累计方差贡献率 (取80%),确定主元个数p,即原始样本的最终特征表示为1个p维向量:

(5)
新观测样本XT的得分向量为:
se=[se1,se2,…,sep]
(6)
(7)

对于新的观测数据,可通过监控统计量T2和SPE进行监测,其表达式如下:
(8)
(9)
式中:T2为观测数据特征与样本数据特征的重合程度;SPE为观测数据与样本数据的偏差程度;Λ为每个主元特征值形成的对角矩阵。

(10)

1.2 MBKPCA方法的改进
MBKPCA通过对输入数据进行分块的方式来解释设备各组成之间存在的固有联系,在一定程度上提高了最终分析结果的精度,但是在整个分块过程中存在以下问题:
(1) 通常直接指定或依据变量采集位置与设备结构之间的关系给出数据分块份数。分块划分过程缺乏依据,各子块表示的实际含义不明确,主观性较强。
(2) 传统的MBKPCA方法缺乏对典型样本选取的过程。因为样本数据的特征过于分散会影响子块数据的特性,弱化各子块数据特征的差异性。分块策略虽然削减了原始变量核矩阵的尺寸,但对每个子块核矩阵的分析仍属于高维空间运算。原始数据量较大时,MBKPCA运算效率也会受到影响。
针对以上问题,笔者采用对应分析方法建立各变量与设备运行工况之间的关联机制,通过样本数据与各个变量的对应分布明确分块份数,提高各个子块中数据的解释能力;应用因子分析方法,合理提取各子块中具有典型特征的数据,提升子块间的特征差异,减少样本总数,提高运算效率。
1.2.1 基于对应分析的分块原则
对应分析方法[13]主要通过对定性变量列联表解析,揭示变量之间、变量和样品(指工况)之间的关系。此方法适用于数量型变量和品质型变量,并且可通过图形直观反映变量与样品之间的关系,便于后续分析结果的揭示与推理。结合MBKPCA方法,可观察变量与设备运行过程的分布情况,以确定分块份数,并根据子块中变量的内容赋予子块一定的含义,具体过程如下:
(1) 根据输入变量结构,构建输入变量矩阵X=(xij)n×m,计算规格化概率矩阵P=(pij)n×m。
(11)
(2) 计算过渡矩阵Z=(zij)n×m,zij可表示为:
(12)


(13)
(14)
(4) 绘制变量点与样本点分布图。载荷矩阵U和V中各元素取值范围相同,元素含义相近,可将载荷矩阵中的数据看成二维点绘制在同一坐标平面,以各点对应的因子载荷值作为坐标值,形成对应分布图。
(5) 在分布图中,载荷矩阵U的点表示变量的分布,V中的点表示样本的分布,即点分布表示变量与样本之间的对应关系。通过对横纵坐标区间的选取,可提取变量与样本集中的点集。其中,点集表示被测对象当前状态下的某一种子状态,点集中样本表示此子状态的表征数据,变量表示影响这一子状态样本数据的主要因素。例如,输入风电机组正常数据,则点集表示设备在机组正常情况下的运行过程。其中,点集中样本数据对应的是MBKPCA中子块的输入数据,区域中变量数据表示的是该子块对应运行过程中的主导变量,点集个数即为分块份数。可进一步综合各子集中变量的物理意义,明确各子集的含义,即子块的物理意义。
1.2.2 基于因子分析的典型样本提取
通过对原始数据的对应分析,确定了MBKPCA分块份数和各运行过程的主导变量。但只说明输入样本数据与各运行过程的分布特性,对数据特征与运行过程特性之间的关系没有做出明确解释。如上所述,在已确定的子块中过于分散的数据特征分布会削弱子块对新数据的分析能力。在高维空间中对过多的数据进行分析,会增加整个算法的运算负担。因此,笔者运用因子分析[14]方法,提取每个子块中的典型数据作为最终样本,以提高子块的解释能力与运算效率。具体过程如下:
(1) 对子块中的数据变量进行标准化处理。
(2) 建立变量间相关系数矩阵,对其进行取样适切性量数(KMO)和巴特利特球度检验,验证所选数据进行因子分析的可行性。
(3) 采用主元分析法计算相关矩阵的特征值和特征向量,通过参数累计方差贡献率确定相关矩阵的主要成分,并对主要成分进行因子旋转,提高主要成分间的差异性。
(4) 利用回归方法计算子块中数据在各主要成分下的得分,提取主要成分得分较高的数据作为样本数据。
重复以上步骤,完成所有子块数据的选取,形成最终的MBKPCA输入样本数据。
2 风电机组故障诊断模型建立
以1.5 MW双馈风电机组为研究对象建立故障诊断模型。根据风电机组结构及运行特点,确定机组正常情况下的模型输入变量;通过对应分析确定MBKPCA分块份数;通过因子分析方法确定样本集;确定机组正常情况下监测统计量的控制上限,作为衡量机组运行是否正常的标准。
2.1 输入变量的确定
按照风电机组结构和功能进行系统边界划分,可分为变桨系统、偏航系统、传动系统和发电机系统。目前绝大部分机组配备数据采集与监视控制系统(SCADA),对机组运行状态进行实时监测。筛选机组SCADA主要运行参数,选择以下参数作为诊断模型的输入:变桨系统主要通过调节桨叶实现机组最大风能跟踪和防止机组过载等功能,主要运行参数包括桨叶角度和风速;偏航系统主要根据实时风向改变机舱位置,保证机舱对风准确,主要运行参数为机舱位置和风向角度;传动系统主要完成转轴升速和传递转矩的任务,运行参数以油温数据为主;发电机系统将旋转机械能转化为电能,主要参数为有功功率。
通过现场调研,发现SCADA系统中机组传动链测点较少。为满足风电机组传动系统状态监测与诊断的要求,在机组传动链特定位置增加振动测点,具体测点位置及描述如表1所示。
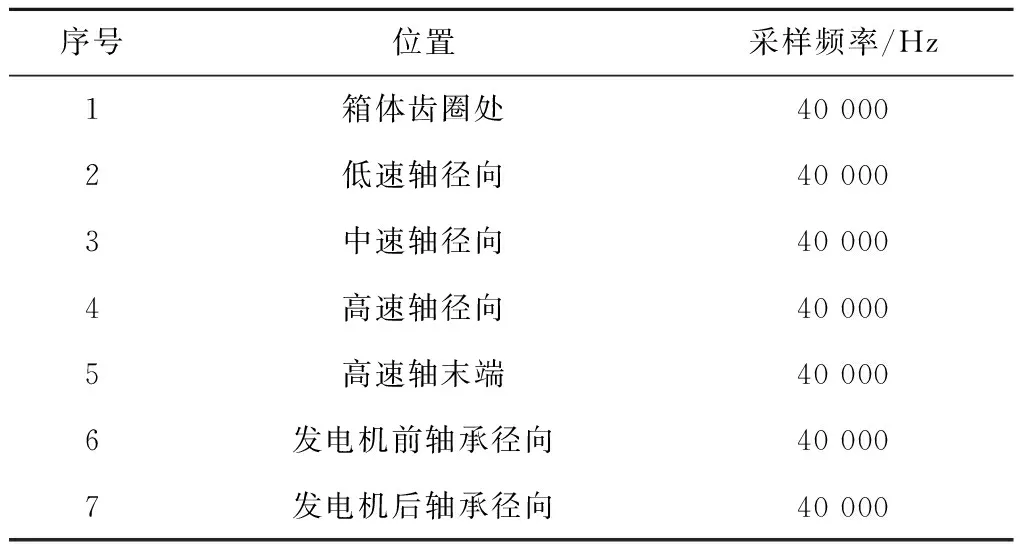
表1 测点位置及描述Tab.1 Arrangement and description of measuring points
对传动链主要组成部件进行结构及运行特点分析,进一步提取振动数据中的有效信息并作为模型输入变量。
齿轮箱结构紧凑,各测点间信号耦合性较强,特征数据易受其他信号干扰,选择无量纲因子[15]范畴中的波形裕度和偏态因子,其变量数值只与设备结构本身有关,与运行工况无关。基于图形学的计算方法可有效避免其他信号干扰对结果带来的影响。
发电机前、后轴承发生故障时,信号特征十分微弱,不易观察,选择J散度和KL散度[16]作为轴承部件的输入变量。
为使模型输入变量能全面反映机组的运行情况,从机组能效角度将各系统效率指标也作为模型的输入变量,主要包括风轮损失、齿轮箱损失和发电机损失[17]。各损失均与主轴转速或主轴转速的倍数有关,所以在最终的变量信息统计中,未独立给出主轴转速。模型输入变量如表2所示。

表2 模型输入变量Tab.2 Input variables of model
基于数据本身特性和数据来源的差异,信号采样频率以所有变量中采样频率最低的数据为准。其中,由SCADA系统获得的机组各类运行数据均为该数据10 min的平均值,其采样频率最低。对于振动参数,为保证数据分析的同步性,计算振动每个采样时刻数据的无量纲因子和散度指标,并取其10 min的平均值作为模型输入数据。
2.2 分块份数的确定
采集风速为11~12 m/s时机组的700组正常数据作为输入变量,表3给出了协方差矩阵R的前4个特征值、方差贡献率和累计方差贡献率。
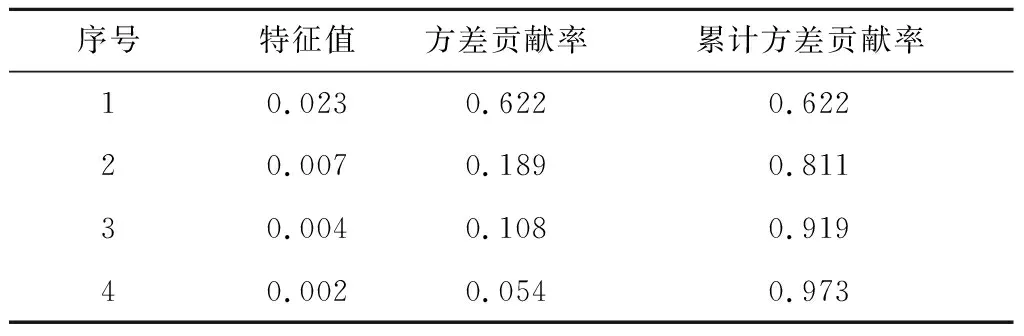
表3 协方差矩阵数据统计Tab.3 Covariance matrix data statistics
由表3可知,输入变量前2个特征值的累计方差贡献率已达到81.1%,说明这2个特征值已经能够表述所有变量的绝大部分信息,故提取前2个特征值,即确定公共因子个数为2。构建R型载荷矩阵U和Q型载荷矩阵V,并根据载荷矩阵中的数据绘制输入样本与变量的对应分布,如图1所示。

图1 输入样本与变量的对应分布Fig.1 Corresponding distribution of input samples and variables
由于第1个公共因子的方差贡献率达62.2%,远高于第2个公共因子,因此图1中以横坐标为分类标准。变量与样本大致可划分为3个点集,即将原始数据划分为3个子块。每个子块中主导变量分别为:子块1变量,包括桨叶角、机舱位置、风向角度、风速和风轮损失;子块2变量,包括波形裕度、油温、偏态因子和齿轮箱损失;子块3变量,包括J散度、KL散度、有功功率和发电机损失。
子块1中的变量主要涉及风电机组能量来源和风能捕获环节,将此子块命名为“能量子块”;子块2中的变量主要与机械能传递环节相关,将此子块命名为“传动子块”;子块3中的变量主要与机组发电环节有关,将此子块命名为“发电子块”。通过机组正常工况下数据点集分布,发现机组整个正常运行状态由多个运行过程(子块)组成,且不同运行过程对变量类型的影响也存在差异。因此,数据的对应分析不仅对每个子块的物理意义作出解释,同时说明其运行状态特性,使后续分析结果的意义更为明确。
2.3 典型样本提取
为提高各子块对机组运行过程的解释能力,并改善模型的运算效率,对每个子块中的数据进行因子分析,寻找具有机组运行过程典型特征的数据作为最终样本。建立每个子块中各变量间的相关系数矩阵,并进行相关性分析,结果如表4所示。

表4 KMO和巴特利特球度检验Tab.4 KMO and bartlett's test
各子块的KMO值均大于0.7,说明各变量之间关联性较强。各子块的巴特利特球状检验概率均为0.00,小于显著性水平0.05,说明样本充足,可进行因子分析。以传动子块为例,计算该子块相关系数矩阵的特征值、方差贡献率和累计方差贡献率,结果如表5所示。
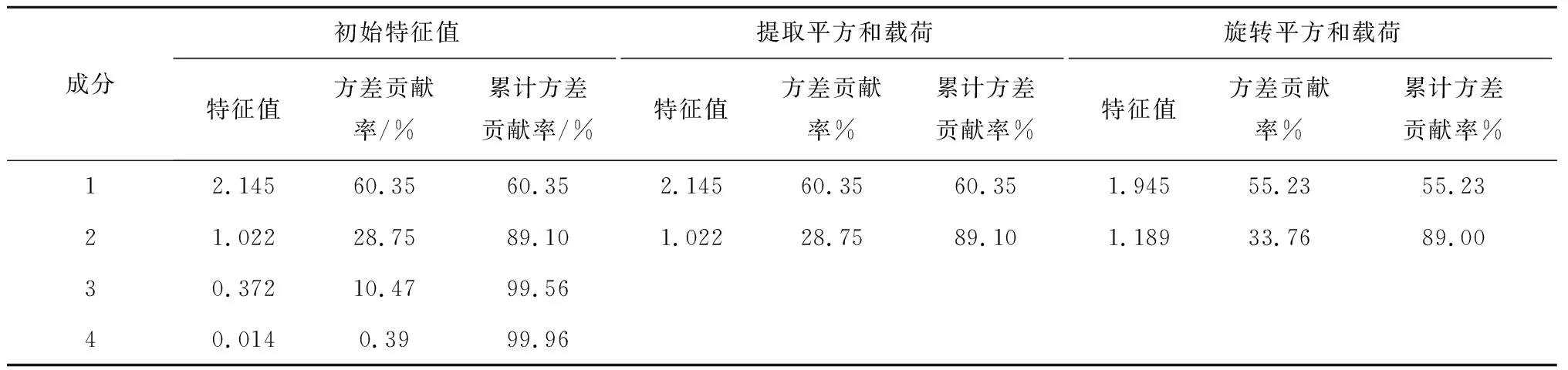
表5 各成分原有指标总方差情况Tab.5 Original indicator and total variance of various components
表5中前2个成分的累计方差贡献率达89.00%,由累计方差贡献率要求(大于80%)可知,这2个成分可表示矩阵中数据的大部分信息,故确定主要成分个数为2。计算主要成分载荷矩阵,并对其进行旋转计算。笔者采用Kaiser方差最大旋转方法计算主要成分与变量间的载荷值,结果如表6所示。
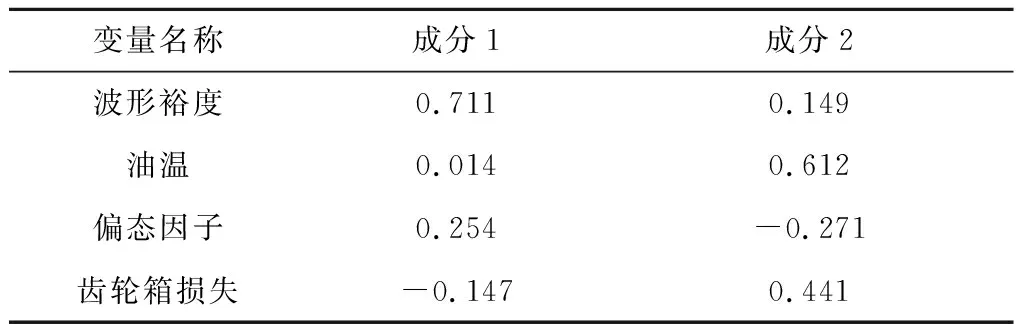
表6 主要成分载荷值Tab.6 Load value of main components
变量间的载荷越高,其在对应成分中包含的信息就越多。成分1中的主要参数与齿轮箱振动相关,此成分称为“振动成分”。成分2中的主要参数与齿轮箱油温和损失有关,该成分称为“温度成分”。采用回归方法计算各成分在样本数据中的得分,结果如表7所示。

表7 各成分得分Tab.7 Component score
样本得分越高,其在对应成分中的解释能力越强,样本的数据特征越具有代表性。因此,按照一定比例提取所有主要成分中的高分样本数据,形成传动子块的典型样本。
同理,对其他2个子块中的数据做相同分析,得出各子块的典型样本,形成最终参与MBKPCA分析的输入样本。样本比例可依照子块中各主要成分方差贡献率进行选取。经因子分析提取出的风电机组样本与变量的对应分布如图2所示。
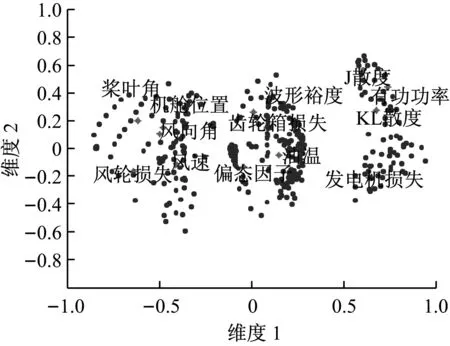
图2 因子分析样本与变量的对应分布Fig.2 Distribution of samples and variables by factor analysis
2.4 机组故障判定

3 实例分析
为验证风电机组故障诊断模型的有效性,以国内某1.5 MW双馈风电机组齿轮箱磨损故障为例进行分析。该机组在2013年2月3日出现解列停机情况,通过查找文件传输协议(FTP)服务器记录,
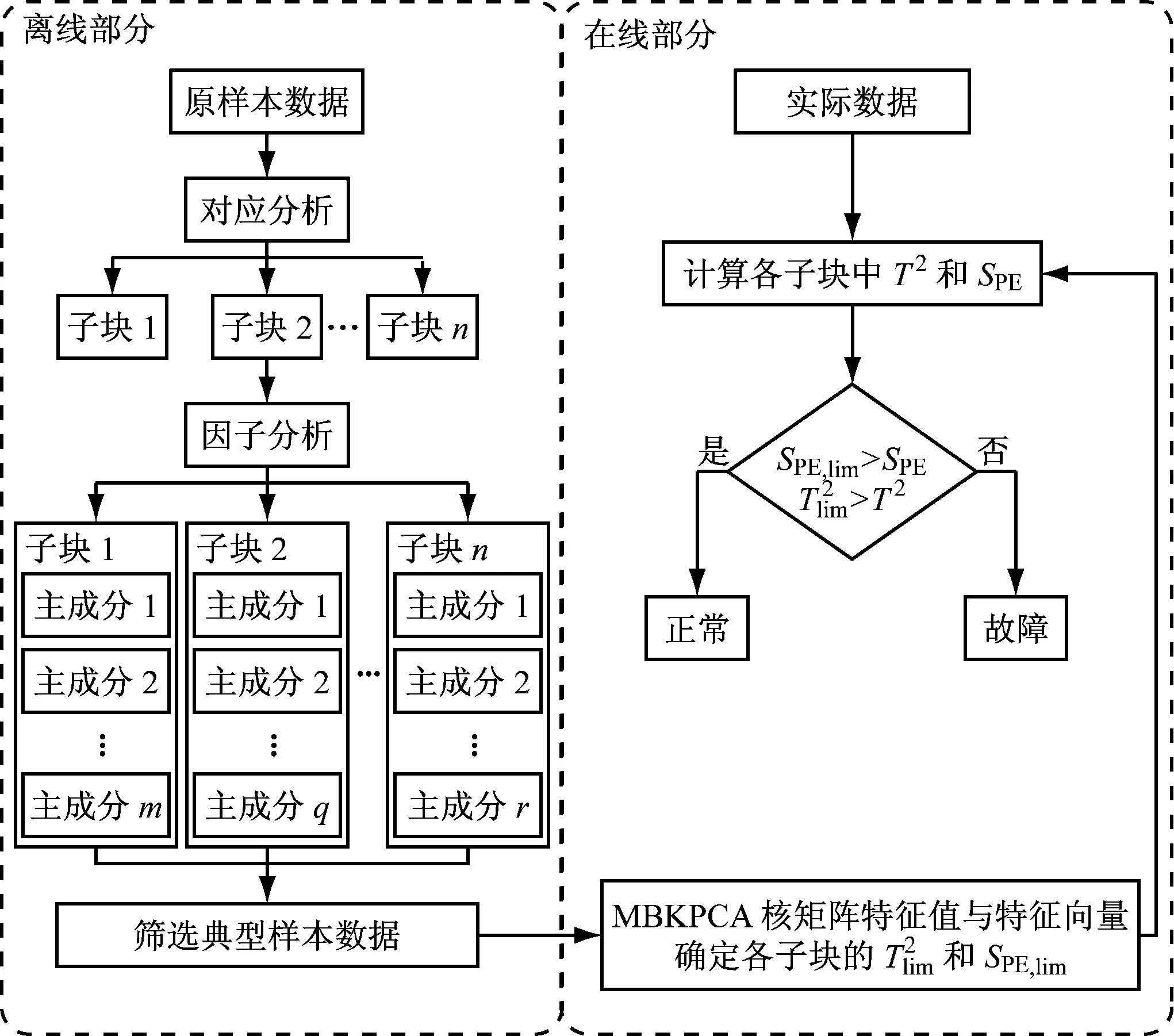
图3 故障诊断流程图
Fig.3 Flow chart of fault diagnosis
风电机组齿轮箱油温过高故障,经现场勘查,发现齿轮箱一级太阳轮磨损严重。提取停机前7天的历史数据,利用所提出的方法对3个子块单元进行监测统计量T2和SPE分析,结果如图4所示。
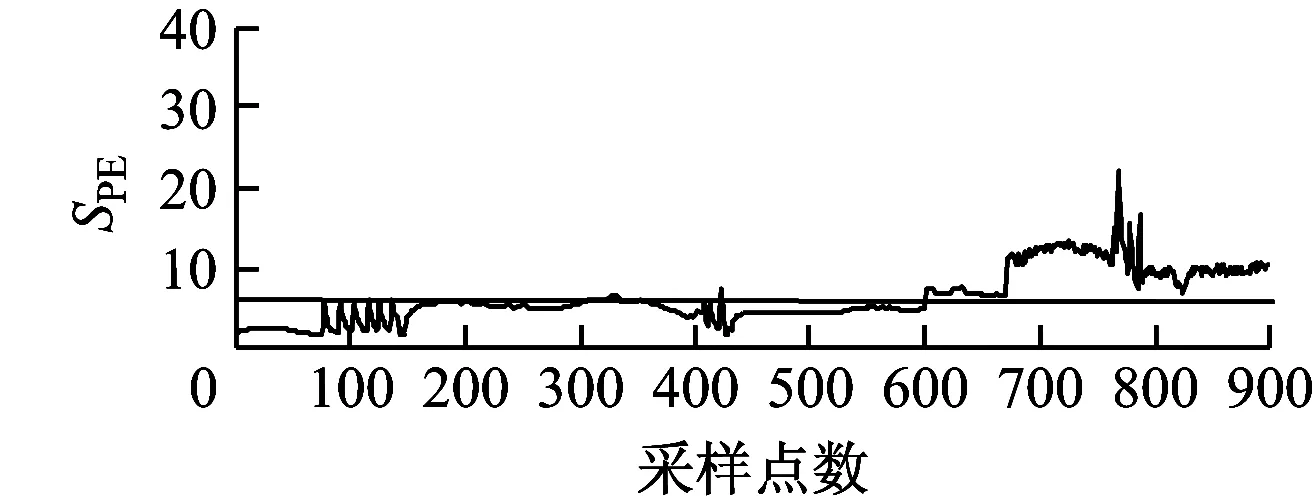

(a) 能量子块统计量结果


(b) 传动子块统计量结果


(c) 发电子块统计量结果图4 改进的MBKPCA方法的故障检测图Fig.4 Fault detection plot by improved MBKPCA method
由图4(b)可知,从第600点开始传动子块的2个统计量显著上升,超过此子块的控制上限,并且数据具有较好的识别持续性。由图5可知,传动子块的统计值明显高于其他子块,且超出阈值,说明机组的传动部分异常。传动子块主要变量为齿轮箱数据,因此诊断为风电机组齿轮箱出现了故障。由图4(a)可知,从600点开始能量子块也出现了统计量数据上升的现象,这是因为主轴与风轮依靠法兰盘连接,属于刚性连接,为齿轮箱振动能量的传递提供了路径。当齿轮箱振动较大时,振动能量可通过主轴传递到风轮,造成风轮数据特征偏离正常运行状态。但风轮不是故障源头,所以偏离程度较小,如图5所示。齿轮箱输出轴与发电机轴之间靠柔性联轴器连接,柔性联轴器不仅补偿了两轴平衡性偏差和角度误差,较强的阻尼性可有效减弱由齿轮箱传递的振动能量,因此齿轮箱故障引起的振动对发电机运行无太大影响,发电子块的统计值最低。综上说明所提出的方法能够有效诊断机组故障,并明确故障发生的具体位置。

(a) 各子块SPE的统计量
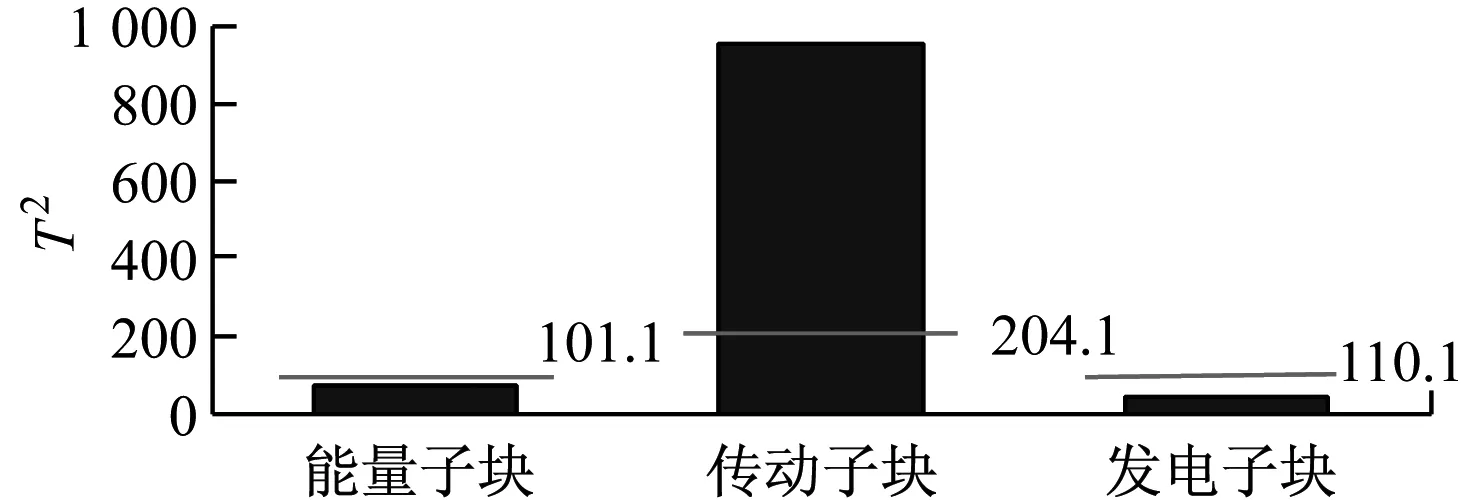
(b) 各子块T2的统计量图5 改进的MBKPCA方法的监测统计量Fig.5 Monitoring statistics by improved MBKPCA method
应用传统MBKPCA方法,样本数据分块按照机组组成结构进行划分,分别为偏航子块、变桨子块、传动子块和发电子块4部分。对同一组故障数据进行分析,结果如图6所示。
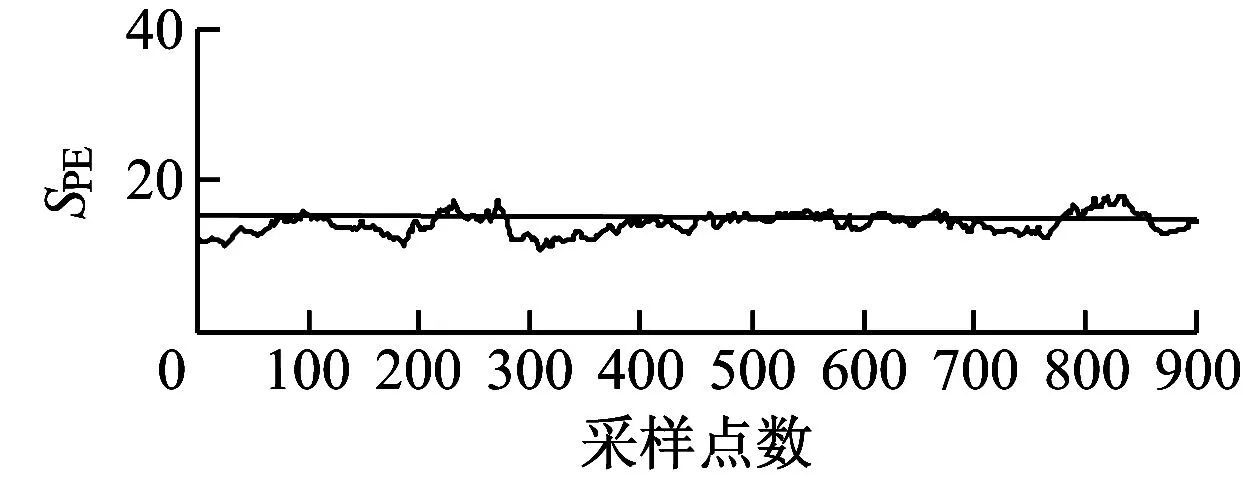

(a) 偏航子块统计量结果
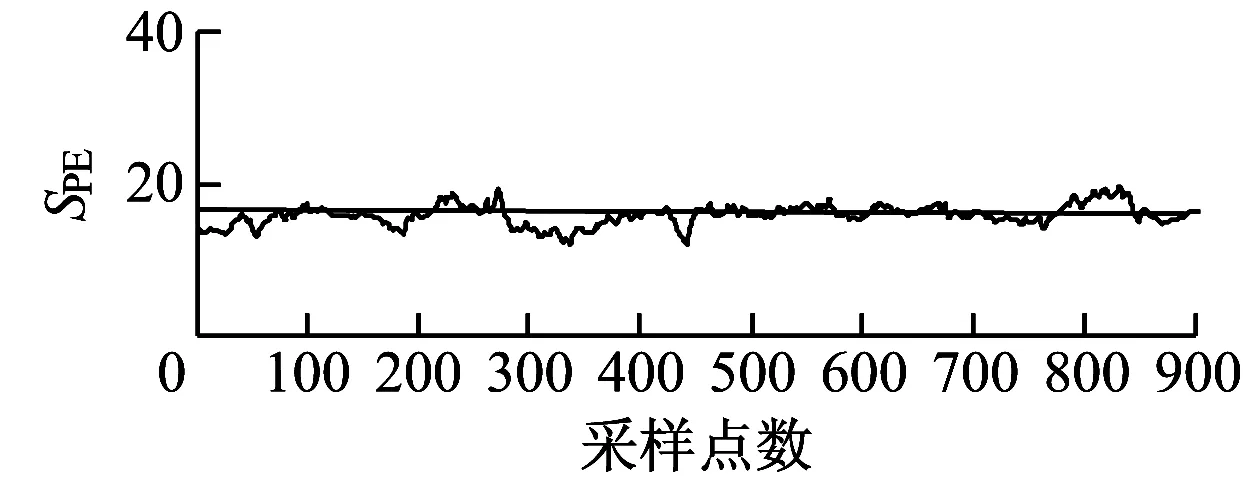

(b) 变桨子块统计量结果


(c) 传动子块统计量结果


(d) 发电子块统计量结果图6 传统MBKPCA方法的故障监测图Fig.6 Fault detection plot by original MBKPCA method
由图6可知,在650点处传动子块统计值超过控制上限,在时间上明显滞后于改进的MBKPCA方法,且数据波动较大。由于传统MBKPCA方法缺少对数据之间关联性的分析,将能量子块拆分为变桨子块和偏航子块,使统计量的趋势变化相比改进的MBKPCA方法不明显,2子块的统计量变化与传动子块未形成对应关系。由图7可知,相比改进的MBKPCA方法,传统MBKPCA方法各子块的统计量差异性较小,偏航子块、变桨子块和传动子块的监测统计量相近,且均接近控制上限,无法明确机组故障发生的确切部位。这说明改进的MBKPCA方法能更及时准确地对风电机组故障作出诊断。
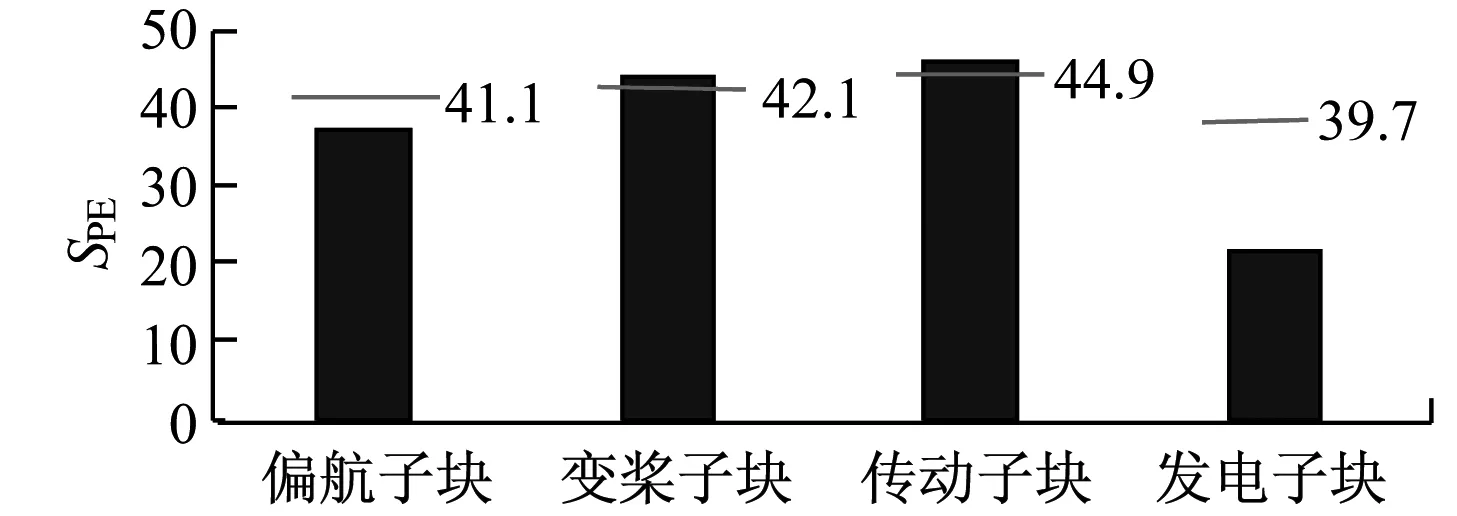
(a) 各子块SPE的统计量

(b) 各子块T2的统计量图7 传统MBKPCA方法的监测统计量Fig.7 Monitoring statistics by original MBKPCA method
4 结 论
(1) 深度挖掘SCADA数据与振动数据信息,引入机组效率、无量纲因子变量和散度指标,提高了数据特征对机组故障的识别能力。
(2) 通过对应分析对传统MBKPCA方法进行改进,明确了机组正常工况下各运行过程的特征,赋予了各子块实际的物理意义,建立了数据与变量之间的关联体系,增强了分块划分的客观性。
(3) 采用因子分析方法分析数据与各运行过程之间的影响程度,提取对每个子块影响程度较大的数据作为改进MBKPCA方法的输入样本,提高了诊断模型的精度与解释能力。
