不确定数据的有效查询处理评估技术研究
2018-10-26金宗安张志刚
金宗安,张志刚
(六安职业技术学院,安徽 六安 237158)
1.引言
许多现实生活中的应用程序产生大量的不确定数据,需要存储、检索和查询这些数据的系统。传统的数据库系统面向存储精确的数据,不适合存储不确定的数据。另一方面,设计不确定数据库来处理概率表示的不确定性,并设置特别的选项来存储具有不确定性的数据。不确定数据库的应用包括信息检索[1],推荐系统[2],移动对象数据管理[3],信息提取[4],数据集成[5]和传感器网络的数据管理[6]等。
由于不确定数据的处理是基于可能世界的,有些针对不确定数据的查询在线性时间内是不可完成的,例如:自连接查询、存在环的连接查询等,而目前并没有有效的方法来判定一个不确定数据的查询是否线性时间内可计算。本文设计算法,把不确定关系中元组分为不相容元组和相互独立元组,有效的评估哪线查询是线性时间内可计算,哪些是不可计算的。
在表 1 Productp、表 2 Order、表 3 Buyerp三个关系中,其中右上角的p表示表1、表3为不确定关系,表1 Productp中name属性为确定属性,memory和color两个属性为不确定属性,第1个元组表示产品iphone 6s plus在

表1 Productp

表2 Order

表3 Buyerp
2.基本定义
定义1 不确定关系:R是一个不确性的关系模式,其中的每一个属性用 Ai表示,i∈{1,2,3,…n,…},A是所有属性的集合,A={A1,A2,…An},每一个属性Ai都有一个域,记为Di,每一个元组x都是不确定性的,x(Ai)表示元组x在属性Ai上的值,不确定关系R上的每一个元组x可以描述为<属性,值>的模式,其中值为 ps,即,这样的关系称为不确定关系。
定义2 不确定属性:不确定关系中的元组发生具有不确定性,因此每一个元组都有一个不确定属性记录它们发生的概率值,记为ps,ps∈(0,1],元组x概率属性ps表示对象x(R-{pS})发生的概率:
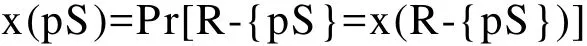
定义3 投影运算π:在不确定关系R中,有k个元组在不确定属性A上具有相同的值,概率分别为p1,p2,…,pk,若它们的关键字属性相同,则此时投影称为不相容事件的投影πPDA,在A属性上投影的概率记为p1+p2+…+pk;若它们的关键字属性不相同,则此时投影称为相互独立事件投影πPIA,在A属性上投影的概率记为 1-(1-p1)(1-p2)…(1-pk)。
定义4 不确定数据连接查询∞p:A、B两个关系的连接查询可以定义为其中c为两个连接查询的条件。由于已经定义了选择和笛卡尔乘积,连接查询可以根据定义来获得,选择查询可能会引入属性之间的依赖关系。两个元组t1和t2分别属于两个不确定关系A、B,它们的概率分别是p1和p2,则两个元组连接查询的概率为p1*p2。
3.不确定数据查询
下面3个标准SQL查询语句及其相应的标识公式,查询语句假设3个关系都是确定性的,不考虑元组的概率属性,查询得到的结果会有一个概率属性值,代表了元组的可信度。
Q1:SELECT DISTINCT name,memory
FROM Productp
WHERE name=‘iphone 6s plus’
Q1(‘iphone 6s plus’,x):-Productp(‘iphone 6s plus’,x,y)
Q2:SELECT DISTINCT address
FROM Buyerp
Q2(v):-Buyerp(u,v)
Q3:SELECT DISTINCT*
FROM Productp,Order,Buyerp
WHERE Productp.name=Order.nameandOrder.orderer=Buyerp.orderer and Productp.color=Order.color
Q3(*):-Productp(x,y,z)
Order(u,x,y,z)
Buyerp(u,v)
在第一个查询语句Q1中,查询不确定关系Productp中name=‘iphone 6s plus’的信息,查询的结果为:

表4 Q1查询结果
对于查询Q1,计算查询结果的概率时,不用列举所有的可能世界,可以从表中直接计算:(1)选择name=‘iphone 6s plus’ 的行;(2) 在 name,memory 上投影;(3)由于第1个元组和第2个元组是不相容元组,投影后的值是一样的,因此要合并元组,合并后的元组概率为之前两个元组的概率之和。
对于查询Q2,计算查询结果概率时,采取与查询Q1相似的方法,但在合并元组过程中,存在相互独立投影,例如对于address=ShangHai条件第一个元组和第三个元组都满足,采用合并的方法消除重复元组,这两个元组进行投影合并时要使用相互独立投影方法计算它们的概率,查询结果如下表所示:
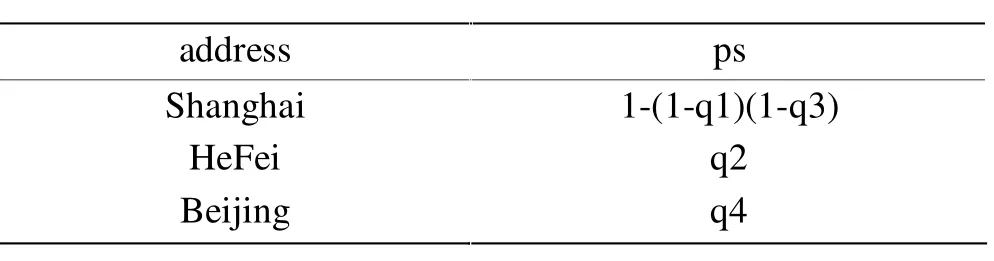
表5 Q2查询结果
第三个查询是多关系连接查询,连接查询只限制了连接条件,查询得到的结果共有4条记录,表中没有重复元组,不需要进行其它操作,查询结果如下表所示:

表6 Q3查询结果
有的查询结果中既有不相容的重复元组,又有相互独立重复元组,此时先要消除不相容,再消除相互独立元组。
4.不确定数据查询算法
在不确定关系中,连接查询要进行有效的评估,因为有些查询在线性时间内能够得到解决,但有些查询对象的多个关系中存在键的约束问题,使得查询不能在线性时间内完成的(#p完全),比如不确定关系的自连接查询,因此要设计有效算法评估哪些查询是线性时间内可计算,哪些是#P完全的。
算法相关的定义如下:
Rels(Q)={R1,…,Rk}是指发生在查询语句Q中的所有不确定关系的集合,假设每个不确定关系至多出现一次。
Attr(Q)表示查询语句Q中所有不确定关系的所有属性集合,Ri.A表示第i个不确定关系R的A属性;
Head(Q)表示查询语句Q中所要查询的属性集合,很显然有
R.Key代表不确定关系R中的关键字属性;
R.NKey代表不确定关系R中的非关键字属性;
Qx表示一个带有x属性的查询Q,则
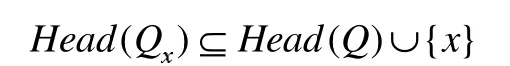
算法1:
if q是一个单个关系查询
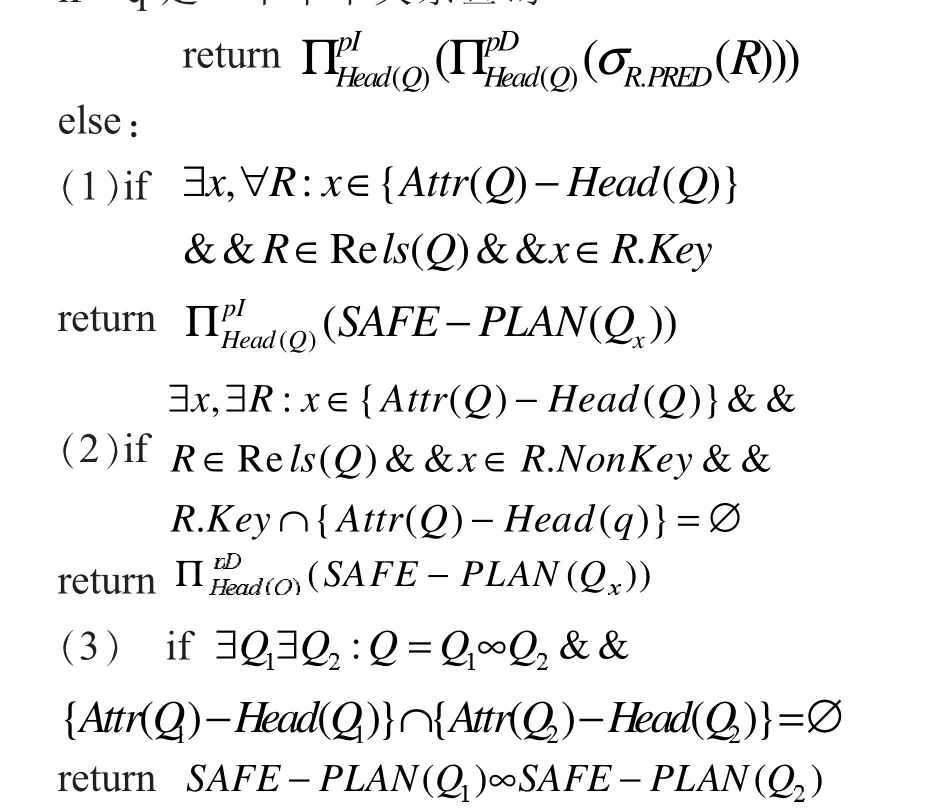
如果不满足以上情况,则返回Q是#P完全的;
在查询评估算法中,如果一个查询只是针对一个不确定关系,只需要按照查询的要求,查询满足条件的数据进行不相容元组投影再相互独立元组投影即可;如果查询的结果中存在不相容的相等元组或相互独立相等的元组,则要分别按照(1)(2)中的方法进行合并操作;如果查询Q可以分解为Q1、Q2两个查询,并且分解的复杂度比原来的小,则可以把原查询分解为Q1、Q2的连接查询。如果查询在上面的方法中都不能得到解决,则这个查询不能正确计算概率。
在概率数据库中,大部分的连接查询结果的计算都是很容易处理的,这些查询都能够在线性的时间内解决,但是一部分连接查询的结果可能会违反一些键约束,因此计算连接查询可能是#P完全的,这部分所讨论的查询不包括自连接查询。
5.实验分析
不确定数据查询的实验环境为Windows 7操作系统,Intel(R)Core(TM)i5-4200M CPU,主频 2.50Ghz,内存4GB,用DataFactory生成不确定数据,数据尺寸s=0.03GB,约100万元组,使用JAVA编程语言实现,实验结果取3次实验平均值。
实验首先测试了10个TPC-H查询中有多少查询不能正确的计算概率(不安全的)。实验对数据进行了优化,把概率为0的元组删除。从表6中可以看出10个TPC-H查询有8个是安全的,能够正确计算概率。Q7和Q8是不安全的查询,这主要是由于查询谓词的不确定性。对数据进行了优化,删除了概率为0的元组,这样处理并不会对查询的结果造成影响,但节约了大量的查询时间,从表6中可以看出优化后的查询时间一般来说较短。

表6 TPC-H 查询时间
由于很多用户只关心查询结果Top-k个元素 (查询结果有N个,k远小于N),而对查询得到的概率很小或k+1到N个查询结果并不是很感兴趣,因此选择TPC-H中Q3、Q9作为查询实验对象,查询元组的返回率为k/N,也就是说当要求返回元组数即为满足查询条件的元组数时,返回率为1。从图中可以看出,当k数量很小时,返回率很低,这样很容易丢失大量的有关联的数据。

表7 不同关联度数据TPC-H查询
表7显示了对不同关联度D=0.3,0.6,0.9分别进行了实验,实验选用了TPC-H中的Q2,Q3,Q5,Q6,Q9,Q10,从表中可以看出不同查询在同一数据上的执行时间不相同,同一查询针对不同关联度的数据处理的时间也是不相同的。总体上,关联度越低,执行的时间越短;相反,关联度越高,执行的时间就越长。这主要是由于随着关联度的增高,可能世界的数量会呈指数级的增长。
6.结束语
本文设计不确定数据查询有效算法,对数据查询进行有效评估,采用不同关联度数据进行实验,实验结果显示,当不确定数据的关联度较低时,数据查询时间较短,而当数据之间关联度比较高时,可能世界数量呈指数级增长,查询时间也会越来越长。但对不确定数据的研究内容还有很多,例如不确定数据的聚集查询、查询优化、自连接查询、不确定数据空值的处理等,一些数据查询的复杂性是#P完全的,这些查询没有有效的计算方法,寻求近似计算的方法来解决此类问题也是研究的一个方向。
