深度卷积神经网络在音乐风格识别中的应用

胡昭华, 余媛媛

1(南京信息工程大学 电子与信息工程学院,南京 210044)2(南京信息工程大学 江苏省大气环境与装备技术协同创新中心,南京 210044)

1 引 言

音乐风格分类是音乐信息检索MIR(Music Information Retrieval)[1]领域非常具有挑战性但又很有前景的任务.由于音乐是一种不断发展的艺术且音乐风格之间没有明确的界限,自动分类音乐风格是一个具有挑战的问题.音乐风格分类问题的关键是音乐信息的特征提取.多种特征提取和分类方法在最近几年相继被提出[2,3],这些分类器的性能高度依赖于按经验所选的手动提取特征的适当性.一般地,识别任务中的特征提取和分类是两个独立的处理阶段,而本文把这两个阶段融合在一起更好地实现了信息间的交互.

最近,深度卷积神经网络CNN(Convolutional Neural Networks)[4]在通用视觉识别任务[5,6]上不断取得显著进步,这激起了人们对于CNN的分类模型[7,8]的研究兴趣.CNN包括了多级处理输入图像,提取多层和高级特征表示.通过共享一些基本的组成部分,可以把许多手动提取的特征和相应的分类方法看作是一个近似或特殊的CNN,然而为了保留有判别力的信息,这些特征和方法必须仔细设计和整合.受CNN在通用视觉识别任务上显著成功的激励,本文将CNN用于具有挑战的音乐风格识别,并研究了网络结构参数的调整对识别率的影响.

Lee[9]是第一个把深度学习应用于音乐内容分析的人,特别是风格和艺术家识别,通过训练一个有2层隐层的卷积深度置信网络CDBN(Convolutional Deep Belief Network)以一种无监督的方式尝试使隐层激活,产生来自预处理频谱的有意义的特征.相比较于那些标准的MFCCs(Mel Frequency Cepstral Coefficients)特征,其深度学习特征有更高的精准度.对于音乐风格识别,Li[10]等人将音乐数据转化为MFCC特征向量输入有3个隐层的卷积神经网络(CNN),最终得出可用CNN自动提取图像特征用于分类的结论,表明CNN具有较强的捕获变化的图像信息特征能力.

本文主要进行了以下几个方面的工作:(1)使用HPSS算法分别从时间和频率方面提取了音乐信号谱图的谐波分量和冲击分量,并将其和原始谱图一起作为CNN网络的输入;(2)详细设计了用于音乐风格分类的基于CNN的深度分类框架,对有效训练一个可靠的CNN所需的多个关键因素进行了研究和实验证明.(3)本文使用对频谱图像进行仿射以及使用PCA改变训练图像中RGB通道的像素值的方法扩充数据集.

2 音乐风格识别算法

本文基于卷积神经网络的音乐风格识别的总体框架如图1所示.首先使用HPSS算法对音乐曲目进行分离,把原始曲目分离成谐波音源和冲击音源;然后对这两种音源及原始曲目分别作短时傅立叶变换,将变换后的谱图输入CNN网络中进行学习,训练以及预测,最后的输出结果即为最终的识别率.

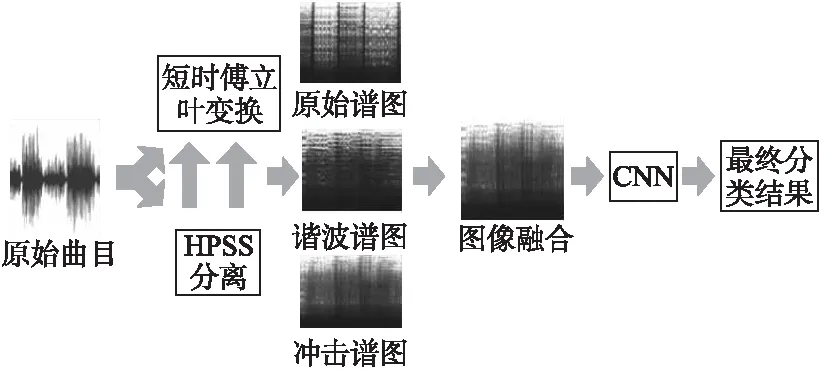
图1 音乐风格识别的流程图Fig.1 Architecture for music genre classification

2.1 Harmonic/Percussive分离算法

音乐信号通常由谐波声音成分和冲击声音成分组成,其具有非常不同的特性.本文使用了分离音乐信号的谐波和冲击声音成分的Harmonics /Percussion 分离算法,其本质是基于频谱图的各向异性连续性的信号分离.这个方法的关键在于其侧重于谐波频谱和冲击频谱的连续方向的差异.谐波频谱通常在时间方向上是连续的,冲击频谱在频率上是连续的.图2是某个音乐曲目的原始频谱及分离后得到的谐波频谱和冲击频谱.从图中可以看出分离后的谐波频谱是在某个固定的频率上沿时间轴连续平滑分布,而冲击频谱是在时间轴上很短而沿频率轴连续平滑分布,而原始频谱中包含有纵向冲击声音与横向的谐波声音.

图2 HPSS算法后的不同谱图Fig.2 Different spectrograms with HPSS algorithm

2.2 网络结构

CNN的网络结构的前几层作为特征提取器通过监督训练自动获取图像特征,在最后一层通过softmax函数进行分类识别.

本文的CNN网络结构如图3所示,其与传统的AlexNet共享基础框架.具体来说,它包含八层,前五层是与pooling层交替的卷积层,剩下三层是用于分类的全连接层.CNN网络的输入图像是使用HPSS分离的谐波谱图和冲击谱图以及原始音乐信号的谱图,并将输入图像大小归一化为256*256,然后将其输入第一个卷积滤波器.在深层网络结构中,第一个卷积层利用96个大小为11*11、步长为4个像素(这是同一核映射中邻近神经元的receptive field中心之间的距离)的核对输入图像进行滤波.接下来max pooling层将第一个卷积层的输出作为输入并和96个大小为3*3的核进行滤波,响应归一化后,第二个卷积层和其输出相连接并用256个大小为5*5的核对其进行滤波.第三、第四和第五个卷积层相互连接,没有任何介于中间的pooling或归一化层,第三个卷积层有384个大小为3*3的核被连接到第二个卷积层的(归一化的、pooling的)输出.第四个卷积层拥有384个大小为3*3的核,第五个卷积层拥有256个大小为3*3的核.使用这五个卷积层,最终获得了256个大小为6*6的特征图,这些特征图被馈送到分别三个含有4096,1000和10个神经元的全连接层.最后一个全连接层的输出便是最终的识别结果.

2.3 网络训练和学习方法

(1)

Pooling层使用的是Max Pooling,在卷积神经网络中卷积层和pooling层都是交替出现的.

输出层与上一层完全连接,其产生的特征向量可以被送到逻辑回归层完成识别任务,所有网络中的权重使用反向传播算法[11]学习.

本文使用随机梯度下降SGD(stochastic gradient descent)训练网络模型,发现较小的权重衰减对模型的学习非常重要,权重衰减可以减少模型的训练误差,因此在本文的实验中微调到0.0005.dropout是训练神经网络过程中一种防止过拟合的技术,通常dropout和动量可以改善学习效果[12].由于所有层使用dropout会使网络收敛花费很长时间,因此在本文的实验中在全连接层设置dropout值为0.5,α=0.9,λ=0.0005.

本文的网络结构中总共有三个全连接层,最后一个全连接层即第八层是输出层,第七层的输出即为其输入,其包含对应m类音乐风格的m个神经元,输出概率为p=[p1,p2,…,pm]T,使用softmax回归公式如下:

(2)

其中X8是softmax 函数的输入,j是被计算的当前类别,j=1,…,m;pj表示第j类的真实输出.

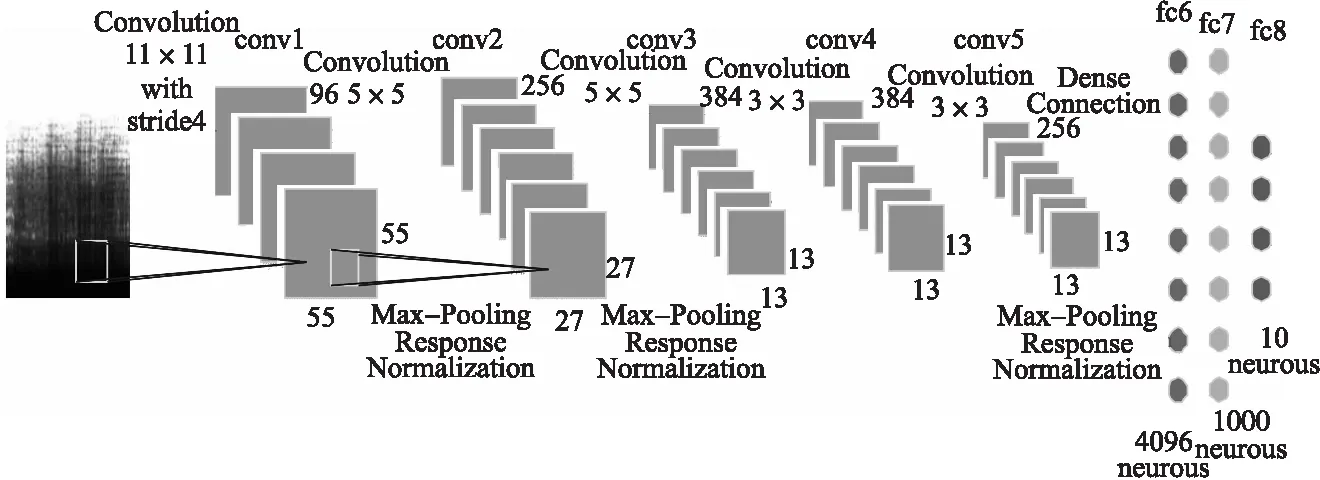
图3 音乐风格识别的CNN结构图Fig.3 Architecture of our deep convolutional neural network for music genre classification

3 实验结果及分析

本文实验中利用caffe框架来训练CNN模型以实现音乐风格的识别.

3.1 数据集

使用识别率作为性能指标,在众所周知的GTZAN风格收集数据库[13]上评估了所提出的方法.GTZAN数据集由Tzanetakis和Cook(2002)收集,由10种类型(蓝调,古典,乡村,迪斯科,嘻哈,爵士,金属,流行,雷鬼和摇滚)组成.每个风格类别包含100个音频录音,长达30秒,共有1000个音乐节选.

3.2 参数优化实验

本文实验表明了正确调整超参数的重要性,超参数可分为两种:模型相关的超参数和训练相关的超参数,如2.2节所示和表1所示.

为了调整这些超参数,数据集按5:1的比例被随机分为二个子集,即2500个音乐曲目用于训练,500个音乐曲目用于测试.

表1 训练相关的超参数
Table 1 Training-relevant hyper-parameters obtained

超参数学习率ηBatch-size动量系数μ权值衰减系数λDropout系数值0.01160.90.00050.5

根据Bengio[14]所述,参数要调整到训练集的错误率变得足够小且稳定的时候.通过该调整过程获得的超参数总结在表1中.

训练相关的超参数可以显著影响网络的收敛和学习速率,它们的影响通过识别率曲线说明,如图4-图7所示.在每张图中,我们集中于一个超参数,而其他的则设置为表1中的最佳值.

图4表示对训练样本进行20000次迭代,学习速率η比较小如0.001时,学习过程会非常缓慢,识别率也尚不稳定.适当提高η可以有效提高学习效率.同时若η过大如0.1会导致学习过程不稳定并且降低分类性能.图5和图6分别说明了动量μ和权重衰减λ的影响.图5表明使用动量μ可以很好地加快学习过程,同时,若μ偏大如0.97,会在初期阶段引起振荡,收敛较慢,此外,它降低了后期阶段的分类性能.图6说明了权重衰减λ的影响,表明较小的λ似乎是一个更安全的选择,而较大的λ如0.005会破坏学习过程的稳定性.

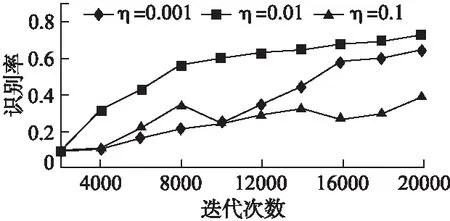
图4 学习率η的影响Fig.4 Impact of learning rate

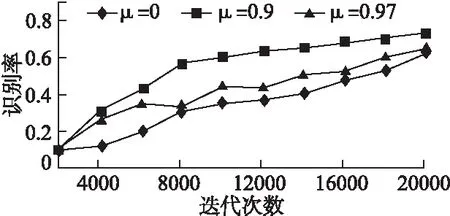
图5 动量系数μ的影响Fig.5 Impact of momentum

图6 衰减系数λ的影响Fig.6 Impact of weight decay

Dropout是训练神经网络过程中防止过拟合的一种技术.在文献[15]中,减少70%输出的dropout应用于最后一个全连接层.本文的实验采取此技术并在每个回合中弄乱训练数据来减轻过拟合.在这种类型的研究中,通常以一定的概率将隐层神经元的输出设置为0,这样此类神经元对正向传播和反向传播都将不起任何作用,因此每输入一个样本,其都使用了不同的网络结构但权值又是共享的,这样求得的参数就能适应不同情况下的网络结构,提高了网络的泛化能力.本实验将dropout微调为0.5或0.6,当增大dropout值时,训练时间稍长一些,收敛较慢,该训练进行了20000次迭代.基于CNN的分类器经过20000次迭代后可以产生良好的分类性能.图7显示了不同的dropout值经过不同的迭代次数有不同的识别率.

总之,CNN中的超参数:学习速率η,动量系数μ,权重衰减系数λ和dropout值可以显著影响网络训练过程,在获得满意的分类性能之前必须仔细调整.在本文的实验中,使用表1中设置的超参数,在数据没扩充的情况下,GTZAN数据集的识别率为73%左右.

图7 dropout值的影响Fig.7 Impact of dropout

3.3 不同音乐风格的识别率比较

表2以混淆矩阵的形式给出了关于音乐风格分类更详细的信息,其中列对应实际的风格,行对应预测的类别,正确分类的百分比位于矩阵的对角线.由于有些音乐风格之间的界限不分明,容易产生误判,比如有的classical音乐的节奏比较强烈,容易被误认为是jazz音乐;而rock音乐由于其广泛的特性容易被误认为其他风格,所以其分类精度相比于其他风格要低一些.

表2 GTZAN数据集的混淆矩阵
Table 2 Confusion matrix for GTZAN dataset

bluesclassicalcountrydiscohiphopjazzmetalpopreggaerockblues82.58.30.00.00.07.30.00.04.70.0classical10.274.60.00.00.012.50.00.00.00.0country0.04.591.70.00.00.00.00.00.00.0disco4.04.14.379.10.00.00.08.312.016.7hiphop0.00.00.00.075.60.00.00.08.10.0jazz3.38.20.00.00.076.20.00.04.50.0metal0.00.00.00.020.20.092.00.04.40.0pop0.00.00.012.00.04.00.082.70.016.0reggae0.00.00.00.00.00.00.00.964.38.4rock0.00.04.38.94.20.08.08.12.058.9

3.4 不同特征图实验比较

表3表明了手工提取时间序列和频率序列的特征并以不同的组合方式放入CNN网络训练,最后会得到不同的效果,其中把3种特征图都输入网络时得到的识别率是最高的,说明只有当训练的特征更全面时才能得到更好的结果.

表3 不同谱图的识别率
Table 3 Classification rate for different spectrograms

图片类型识别率Original Spectrograms67%Harmonic Spectrograms58%Percussive Spectrograms60%Original + Harmonic + Percussive Spectrograms73%

3.5 数据扩充实验对比

本文主要使用仿射变换以及用PCA改变训练图像中RGB通道的像素值这两种方法对图像数据进行扩充.

表4是对音乐曲目的图像进行扩充后得到的实验结果图,从此表中可以看出扩充实验数据对本实验结果具有改善作用.因此数据扩充已经成为生成更多图像样本和应对各种差异获得鲁棒性的重要方式.然而本文的实验结果识别率偏低,经分析发现:音乐曲目的变化是非常丰富的,因此使用100首曲目来代表一种特定类型的各种变体是不够的,而且相较于8层的网络结构来说本文的训练数据是偏少的,以至于最终的分类结果不是特别理想.可以预见随着音乐曲目的增多,本文的识别效果将会进一步提升.

表4 扩充实验数据后的识别率
Table 4 Classification rate with data augmentation

图片类型识别率Original Spectrograms68%Harmonic Spectrograms60%Percussive Spectrograms63%Original + Harmonic + Percussive Spectrograms77%

3.6 与其他方法的准确率对比

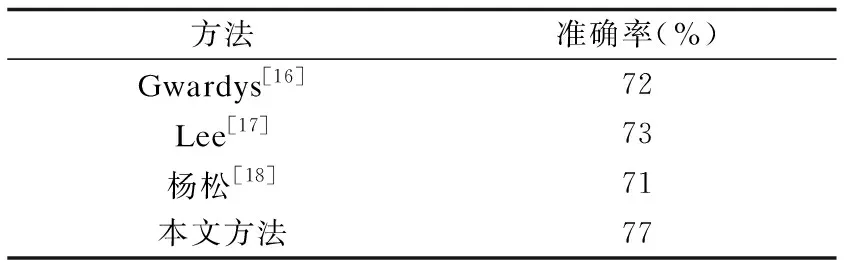
当前有很多学者针对音乐风格识别提出了不同的研究方法,如表5所示,Gwardys[16]也使用了HPSS算法获得频谱图,而后微调了一个8层网络,最终获得72%的准确率,而本文使用此频谱图训练了此8层网络,准确率有所提升.Lee[17]训练了一个只有2层的CDBN,其识别模型的深度比本文的浅,数据量也比本文的少,但实验结果很接近本文扩充数据前的正确率,由此可见小数据集在浅层网络里也能有较好的结果.杨松[18]运用了传统机器学习方法中的K均值聚类来进行音乐识别,其识别率为71%,本文提出的深度学习方法相比较下分类准确率有一定的提升.

表5 本文方法与其他方法比较
Table 5 Comparison to other state-of-the-art methods

方法准确率(%)Gwardys[16]72Lee[17]73杨松[18]71本文方法77

4 总 结

本文提出了一种基于卷积神经网络的音乐风格识别方法,详细设计了该方法使用的网络框架并研究了一些影响其分类性能的关键因素.起初使用原始谱图进行实验时,得到的识别率只有67%,为了改善结果,实施了harmonic/percussive分离实验,最后识别率提高了6%.此外本次实验表明了数据扩充的重要性和有效性,特别是训练数据不够时,当把本次实验数据扩充后,实验效果改善了3%.

本文的实验取得了一定的识别率,使用了卷积神经网络的框架,再加上数据扩充等手段,使得深度学习应用于小数据集成为可能,并取得了一定的判别能力.在将来的工作中,一方面通过搜集每种风格更多的音乐曲目来提高识别率,另一方面可以构造混合网络结构,如卷积神经网络和循环神经网络,可利用卷积神经网络提取局部特征,循环神经网络对这些提取的特征作时间上的整合,由于循环神经网络对前面的信息具有记忆功能,可使提取的特征更具有整体性和连贯性,提高识别结果.