基于遗传算法的多分区结构化网格自动优化分区的研究

赵 璐 刘 勇 张 祥 岳孟赫

(南京航空航天大学能源与动力学院 江苏 南京 210016)

0 引 言

随着计算流体力学CFD己成为一门独立的学科，而且在能源、环境、航空、航天、船舶等许多科学研和工程应用领域中发挥着日益显著的作用，现在对于很多工程上的问题都是先进行数值模拟，得到理想的结果后再进行实验论证[1]。数值模拟的第一步是建立模型并生成网格，网格质量的好坏严重影响到数值解的收敛性和精度。结构化网格的求解精度高，是三维工程分析的首选单元类型。对于结构简单的模型来说，ICEM、Gambit等软件可以在短时间内对模型划分出高质量的网格。然而在面对复杂结构，例如带冷却结构的涡轮叶片结构化网格生成的工作量很大。在建立网格上所花的人力时间比在分析物理解所花的人力时间高出许多倍，而且网格质量也并不能达到最优化。当前对于边界形状复杂的六面体几何体，不能直接生成相应的结构化网格。通常的做法是用手工方法将全局域中的区域分解成几何形状规则的子域，然后在各子域内进行网格映射。在这个过程中存在以下几个问题：

1) 手工方法耗时长，且不具有普适性；

2) 不能确定各子域的质量是否最优。

为了解决这些问题，代星等[2]引入顶点分类理论对复杂多边形子域的边界进行简化，但只提出了对于圆形和三角形区域划分子域的方法，不具有普适性。White等[3]提出了一种可以自动划分分区的方法，但此方法只适用于可扫略的几何图形，不能用于分解复杂模型。目前对于复杂形体，尚缺乏具有高效性、高质量的结构化分区网格自动优化方法。Jonathan[4]根据厚/薄分解方法提出了一种自动分解复杂几何体的方法，但此方法划分出来的长/细区域适用于结构化网格，剩余子区域适用于非结构化网格。目前对于复杂形体，尚缺乏具有高效性、高质量的结构化分区网格自动优化方法。

针对以上问题，本文首先建立分区的评价指标，然后将分区的产生构造成一个寻找此指标最佳的优化过程，最后采用遗传算法[5-9]来进行分区寻优。通过组合基本的二进制编码来表述分区切割点的空间位置信息，以自动求得结构化的优化分区。

1 分区质量评价体系

设计一个结构化网格分区优化算法的第一步是要先确定结构化网格分区的质量。近几十年来，网格优化技术的研究一直是人们研究的重点内容，各大商业软件中也有对网格质量进行评价的指标，如雅可比、正交性和纵横比[10]等。本文基于结构化网格质量的度量对分区质量进行了深入的研究，提出了一套分区质量评价体系。网格分区评价体系基于以下几个指标。(1) 翘曲度η(-1≤η≤1，理想值为1)；(2) 歪斜度Ω(0≤Ω≤1，理想值为1)；(3) 相似度ε(0≤ε≤1，理想值为1)。对于标准长方体分区，这些参数均为1。

1.1 分区结构

结构化分区为六面体结构，本文规定其六个面分别为E、S、W、N、T、B。其中E面与W面互为对应面，S面与N面互为对应面，T面与B面互为对应面。每个面有四条边，分别记为e、s、w、n，边e与边w相对应，边s和边n相对应。分区结构越接近于长方体，划分出的网格质量也就越高。由于模型几何结构的限制，分区结构通常为不规则的六面体，即分区存在扭曲的不规则面，分区面间存在过大或过小的夹角。如图1所示，(a) 为理想分区，(b) 为工程中经常遇到的不规则分区。对于各种不规则的分区结构，由于缺乏经验，直接划分出高品质的结构化网格的概率比较低。因而需对分区结构进行优化使之接近规则分区，以便划分结构化网格。

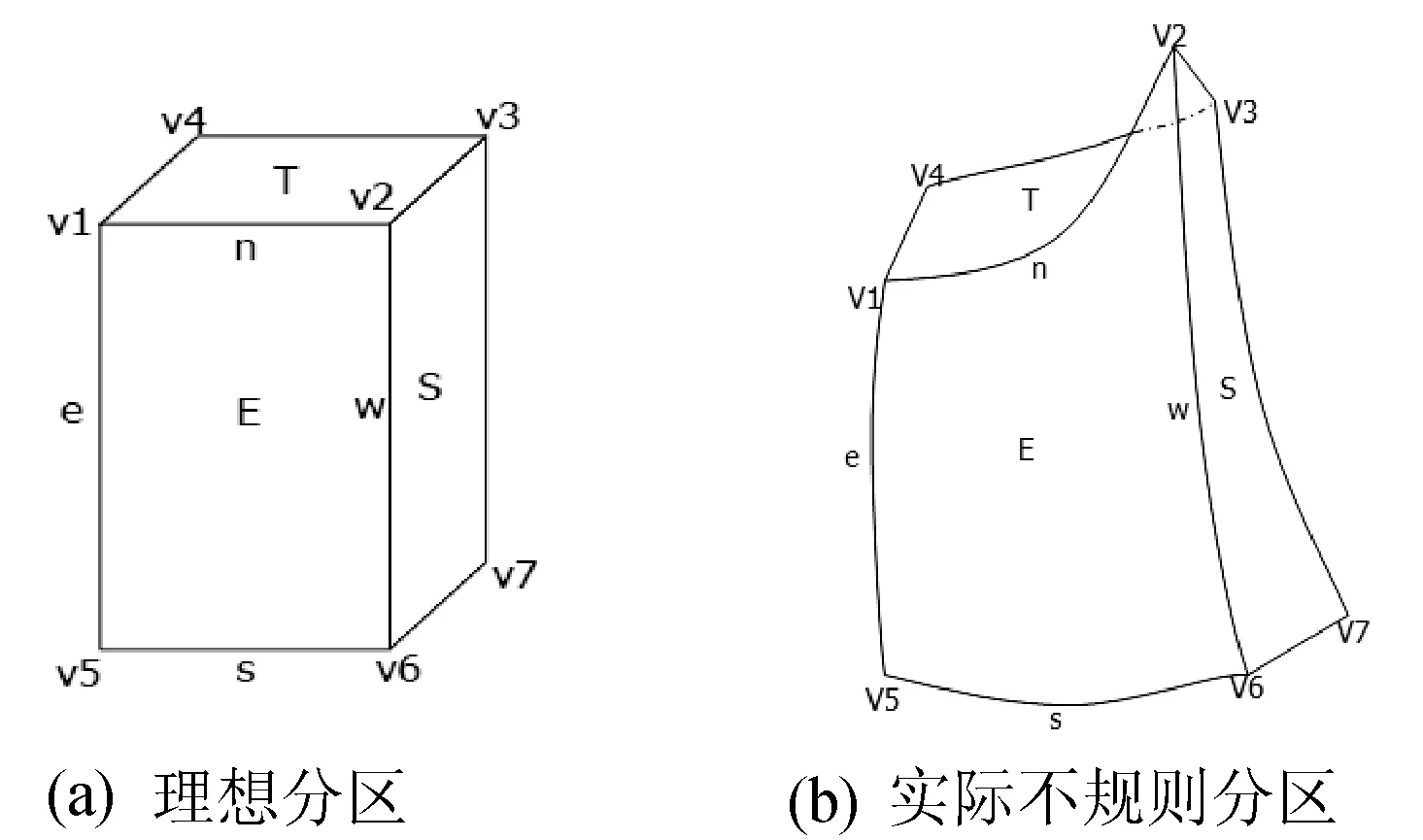
图1 分区结构

1.2 分区质量指标

1.2.1 翘曲度η

翘曲度表征了分区面的翘曲程度，面外翘曲发生在分区面的四个顶点不共面的情况下。该指标的计算过程如下：分区面的四个顶点共可划分出两对三角形，依次计算每对三角形所构成的面的夹角θ，寻找出最大值，并按照线性关系将角度进行归一化，即为翘曲度η，如图2所示。当四个点共面时，θ=0。当出现两个三角形面片法向逆向时，-1<η<0，此时分区极有可能产生负体积网格。

(1)

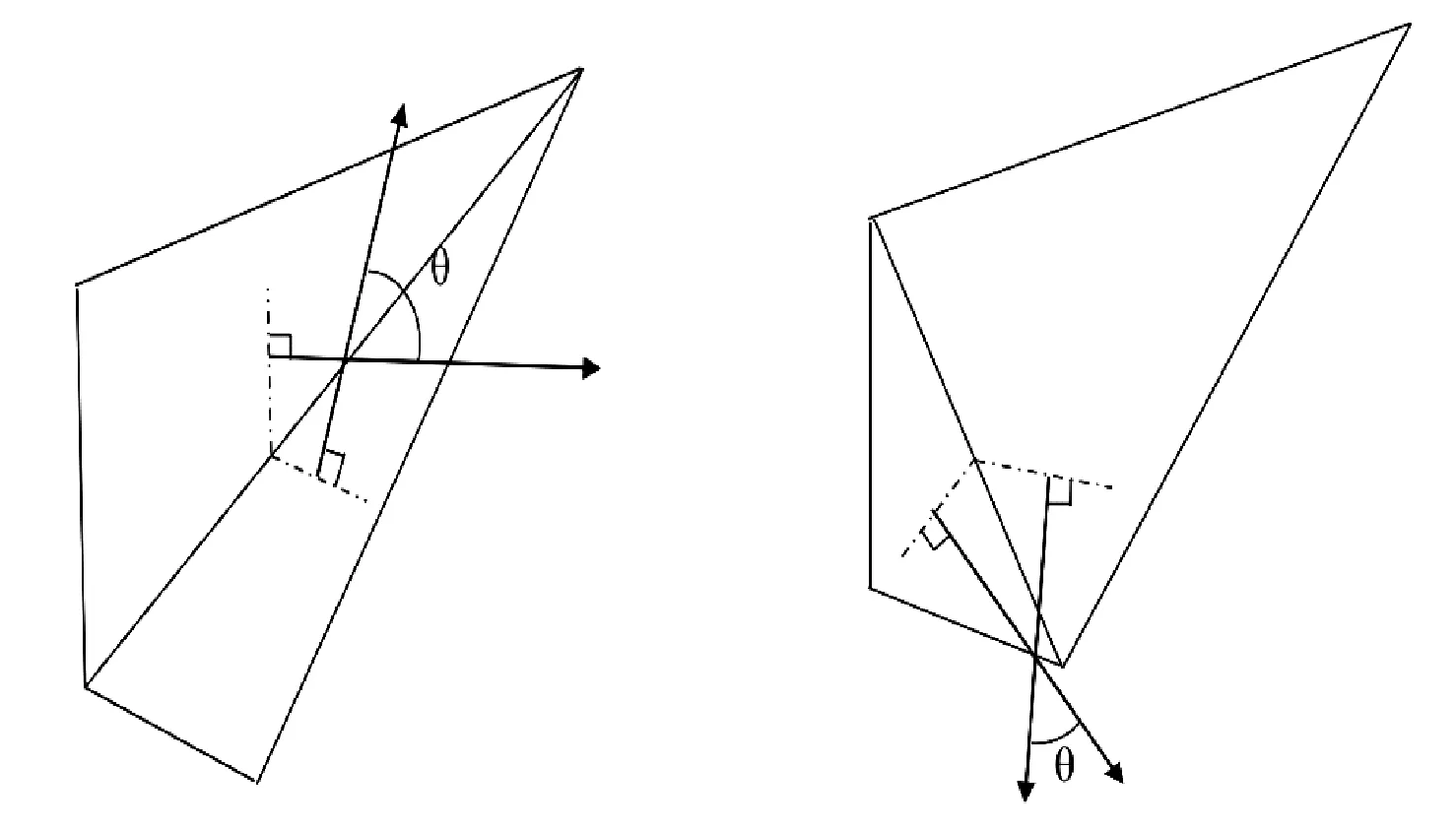
图2 分区翘曲

1.2.2 歪斜度Ω

歪斜度表征了分区面内的歪斜程度，反应了该分区面与矩形的类似程度。该指标的计算过程如下：四个顶点对应四个角，依次计算四个空间角度值θ，寻找出最大和最小的角度值，并按照线性关系进行归一化，其中最小的数值解即为歪斜度Ω。

(2)

1.2.3 相似度ε

相似度表征了分区对应曲面的相似程度，包括对应线相似度ε1，对应角相似度ε2和对应面积相似度ε3。该指标的计算过程如下：

(1) 结构化分区共有三组对应边：(T.s=>T.n=>B.s=>B.n)、(T.w=>T.e=>B.w=>B.e)、(E.e=>E.w=>W.e=>W.w)，每组对应边共有四条线，依次计算每组对应边每条线的长度，每组对应边中最短长度与最大长度之比为ξa。

(3)

对应线相似ε1则为

ε1=(ξa1,ξa2,ξa3)min

(4)

(2) 结构化分区共有十二组对应角，每组对应角共有两个角，依次计算每组对应角每个角的角度θ，最小角与最大角的比值为ξb。

(5)

对应角相似度则为:

ε2=(ξb1,ξb2,ξb3,…,ξb12)min

(6)

(3) 结构化分区中共包含三组对应面：(T=>B)、(E=>W)、(S=>N)每组对应面包含两个面，每组对应面中最小面面积与最大面面积之比为ξc。

对应面积相似度则为:

ε3=(ξc1,ξc2,ξc3)min

(7)

目前大体上有两种定义网格质量的方法[11]，一类是将网格质量定义为所有单元质量的总和或平均值[12]，另一类是以网格中最差的一个单元质量来表示整个网格的质量[13-14]。为了在优化过程中分区质量的改进有一定的取向性，使尽可能多的低质量分区变为高质量分区，本文参照网格质量定义的方法，选用分区质量度量中最差的一个指标来表示整个分区的质量Q。

Q=(η,Ω,ε1,ε2,ε3)min

(8)

2 优化遗传算法

2.1 问题描述

为了自动划分最优结构化分区，首先要确定好几何体上一些特征结构的位置：比如叶片上的气膜孔列、扰流柱、尾缘劈缝和挡板等结构变化的位置。这些位置会在固体域的内外表面产生必须的结构分区，从而产生一些固定点。本文优化算法的思路是通过几何特征计算得到每个分区产生的固定点，之后用遗传算法确定切割点，使得这个分区的质量达到最优。如图3所示，在这个复杂几何体中，固定点为A1，A2，…，A6，C1，C2，…，C6，切割点为B1，B2，…，B6。如何优化确定Bi系列的切割点，本文采用了两种办法：串行优化和整体优化。串行优化是对分区依次进行优化，当第一个分区优化结束后再对第二个分区优化，以此类推，直至最后一个分区优化结束，每一次优化都使得当前分区质量指标最高。在算法上表现为从起点开始逐次确定Bi点对，如图3中，首先通过优化算法确定(B1B2)，然后再确定(B3B4)，依此类推将Bi点全部优化完。整体优化是对所有分区同时进行优化，优化结果确保所有分区的平均质量指标最高。在算法上表现为同时将所有Bi点作为待求点，通过优化算法一次性确定这些点。两种优化算法均为了优化结构化分区，提高分区网格质量。

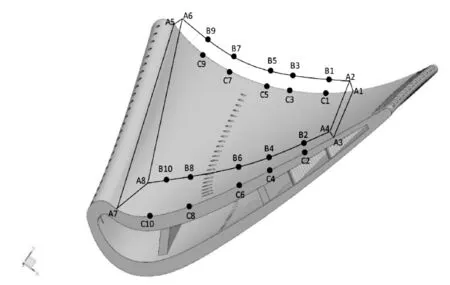
图3 结构化分区计算示意图

2.2 串行优化遗传算法

串行算法的步骤为：

步骤1首先根据A1、A2、A3、A4、C1、C2为已知点，在边A4-A8(顶边)和A2-A6(底边)上分别确定点B2、B1，使A1、A2、A3、A4、C1、C2、B1、B2这八个点形成第一个最优分区。

步骤2根据C1、C2、C3、C4、B1、B2为已知点，在边B2-A8(顶边)和B1-A6(底边)上分别确定点B4、B3，使C1、C2、C3、C4、B1、B2、B3、B4这八个点形成第二个最优分区。

步骤3依此计算，当计算最后节点对，即B9、B10时，要同时保证最后两个分区都为最优，避免最后一个分区质量变差。

首先对个体染色体进行编码。由于同时求解的是两个变量，所以采用一个二元值val[2]来表征一个染色体，每个值采用传统的32位二进制串来表示(0～1)之间的浮点值，该浮点值表征该点在求解域中的比例位置：

(9)

因此B1和B2点的计算公式为：

B1=A2+val[0](A2-A6)

(10)

B2=A4+val[1](A4-A8)

(11)

其次随机产生初始种群，种群规模大小可根据实际情况设定。之后进行适应度计算。遗传算法中以个体适应度大小来判断各个个体的优劣程度，从而决定每个个体的遗传概率。在本算法中，目标函数即为分区的质量度量Q。

质量度量总是非负的，且优化目标是求得目标函数的最大值，因此直接将目标函数设为个体的适应度。此方法是依次对每个分区寻优，因而适应度f则是单个分区的质量度量。

f=Q[i]=(η[i],Ω[i],ε1[i],ε2[i],ε3[i])min

(12)

式中：i代表第i个分区。

最后依次进行选择运算、交叉运算和变异运算。选择运算会将当前群体中适应度较高的个体按照某种准则传递到下一群体中去。其具体操作是计算每个个体的适应度fi与当前群体中所有个体适应度的总和的比值，即个体的相对适应度fref：

(13)

相对适应度就是每个个体被传递到下一代群体中的概率。最后随机产生一个0到1之间的数，依据这个随机数出现在上述哪个概率内来确定每个个体被选择的次数。交叉运算以某一概率互相交换某两个个体间的部分染色体。本算法选用单点交叉法，其具体操作是对群体中个体的染色体设置交叉点位置并进行随机配对，互相交换配对的两个染色体间的基因。变异运算是对某个或某些基因值按某一小概率进行改变。本算法选用基本位变异法，具体操作为确定每个个体上基因变异的位置，根据一小概率将变异点位置的基因值取反。对当代群体进行选择、交叉、变异运算后可以得到一个新的群体。遗传算法的终止条件有两类常见条件，一类是设定最大进化代数；另一类是根据个体的差异来判断，即所有基因位相似程度来进行控制。针对本文问题，设定最大进化代数简单易行，且可以得到较为精确的最优解，因此选取设定最大进化代数作为遗传算法的终止条件。经过迭代运算，求得最优分区。当此分区优化完成后，此分区计算得出的上点和下点则变为下一分区的确定点，如此再进行下一分区的优化。

2.3 整体优化遗传算法

整体优化时，染色体中的二元值对的个数n是变值，根据具体的问题由外部确定，例如在图3所示的实例中，n=5。染色体中采用二维数组来表示个体：val[n][2]。每个二进制串翻译成0～1之间的值，表示该点在顶边和底边上的比例位置。为了保证这些点的顺序：例如B4在B2-A8之间，B6在B4-A8之间等等，除第一对点以后的每对点的比例位置需要重新计算：

B2=A4+val[0][0](A4-A8)

(14)

B4=B2+val[1][0](B2-A8)=A4+

[val[0][0]+val[1][0](1+val[0][0])](A4-A8)

(15)

…

本算法旨在使得所有分区的质量平均，因而目标函数即为所有分区网格的质量度量的平均值。个体的适应度f为：

(16)

式中：i代表第i个分区。

3 优化应用

为了证明这两种优化算法的适用性，本文选取航空发动机中具有代表性的涡轮叶片作为分区优化对象。

现代的涡轮叶片都设计为结构复杂的空心叶片，其主要部分为叶身、缘板和榫头三部分。由于这个几何体的的各个部分间存在着类似结构，故选取叶盆侧尾缘-前缘之间的结构进行优化，如图3所示。其中A1-A3-A7-A5面为叶盆固体的外表面，A2-A4-A8-A6为计算域的外流场边界。面A1-A3-C2-C1中包含了一列扰流柱，这在固体域的内外表面产生必须的结构分区，故本例中C1-C2为已知点，由叶盆表面结构确定。对应面的点B1-B2则由本文提出的优化算法所确定。同理，点C3-C4,C5-C6,C7-C8,C9-C10都为已知的固定点，通过优化算法求得对应的切割点：B3-B4,B5-B6,B7-B8,B9-B10。

本例中共需划分6个分区：P1，P2，P3，P4，P5，P6，如图4所示。串行优化算法的思想是依次优化每个分区，即首先根据固定点C1-C2确定P1分区的两个切割点B1-B2。当此区域优化完成后，点B1-B2随之成为P2分区的固定点，由此确定P2分区的切割点B3-B4。如此依次优化，直至求得P6分区的切割点B9-B10，优化结束。整体优化算法是一种多变量寻优的方法，因而需保证点与点之间位置关系的正确性(B3在B1与B5之间，B5在B3与B7之间，B7在B5与B9之间，B9在B7与A6之间，B4在B2与B6之间，B6在B4与B8之间，B8在B6与B10之间，B10在B8与A8之间)。约束这些点的位置之后则可根据目标函数同时确定切割点B1-B2,B3-B4,B5-B6,B7-B8,B9-B10的位置。

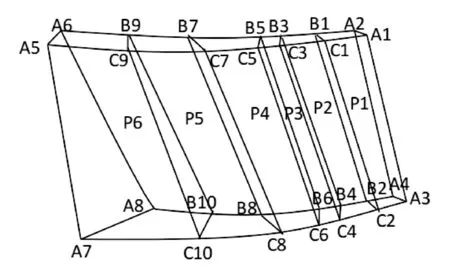
图4 叶盆分区

为了更清楚地展现出优化分区，将叶片结构进行隐藏。对同一计算域，两种优化算法划分出的分区如图5、图6所示。

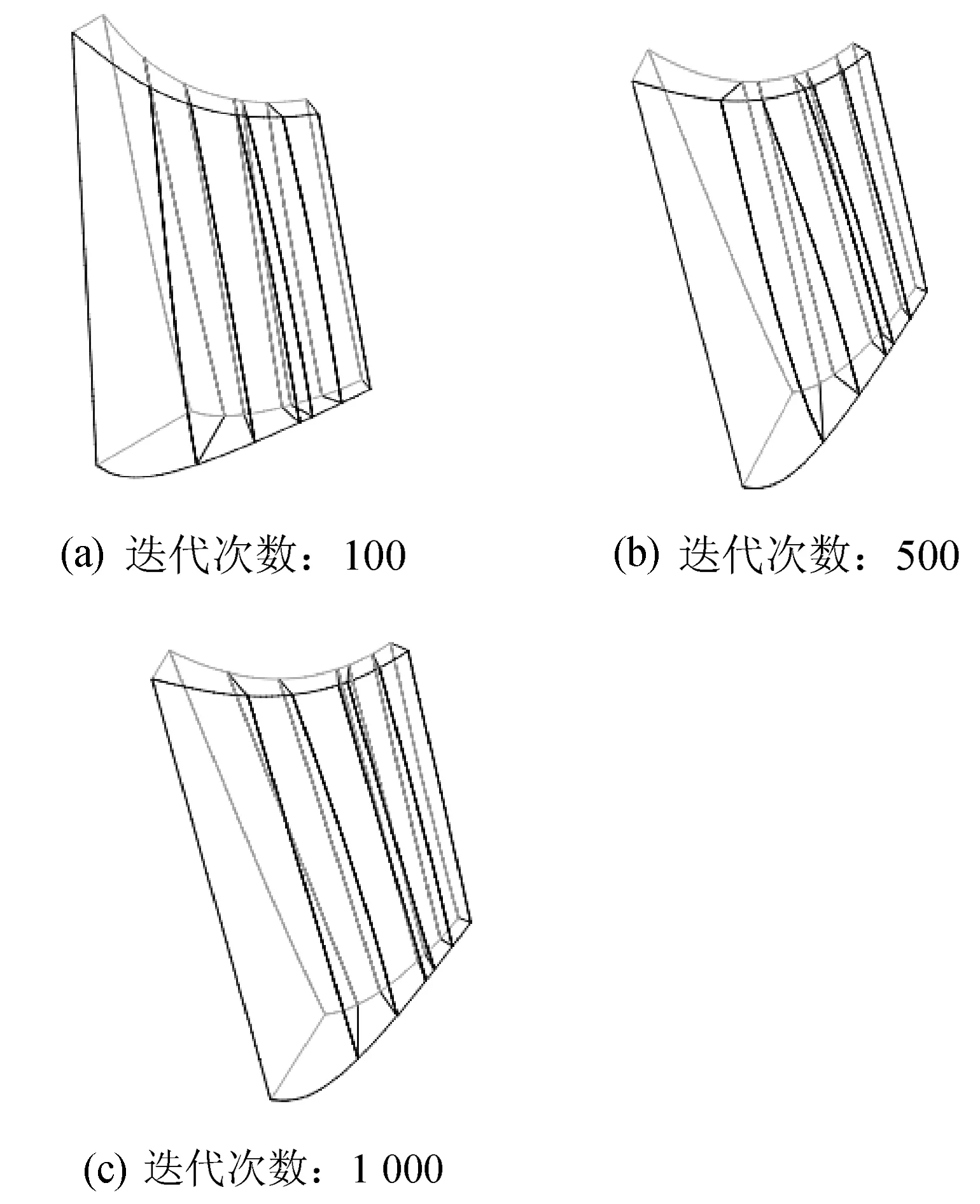
图5 串行优化算法划分的分区

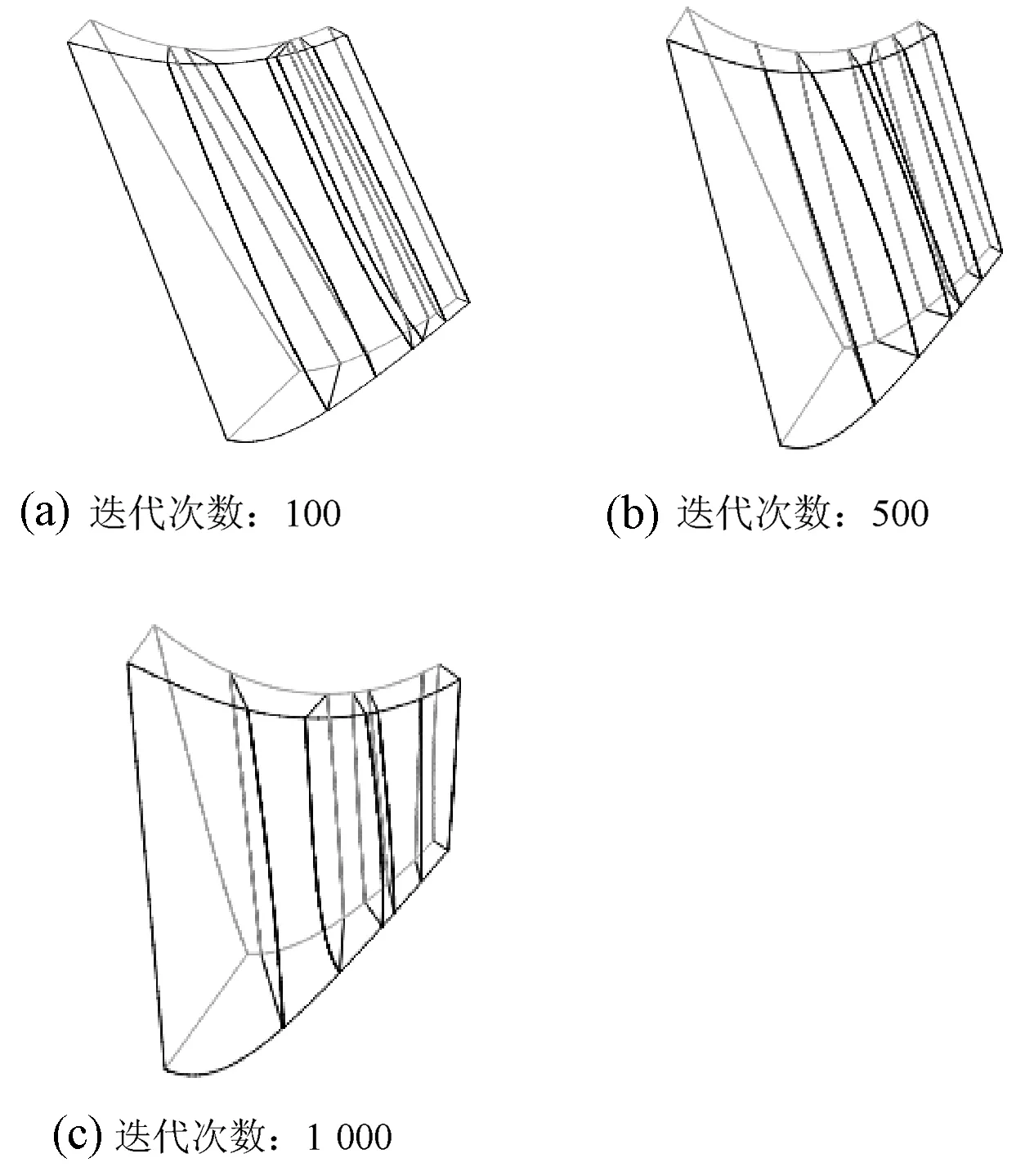
图6 串行优化算法划分的分区

4 结果分析

整个涡轮叶片分为外流场、固体域、内流场和榫头四部分。外流场共划分了47个分区，固体域划分了30个分区，内流场划分了85个分区，榫头划分了4个分区，此工作量十分繁重。本文利用这两种优化算法分别对叶片进行了分区处理，并进行了比较。

应用本文开发的涡轮叶片管理软件及提出的评价分区质量体系分别对两种优化方法划分出的分区进行质量检验，如图7所示。

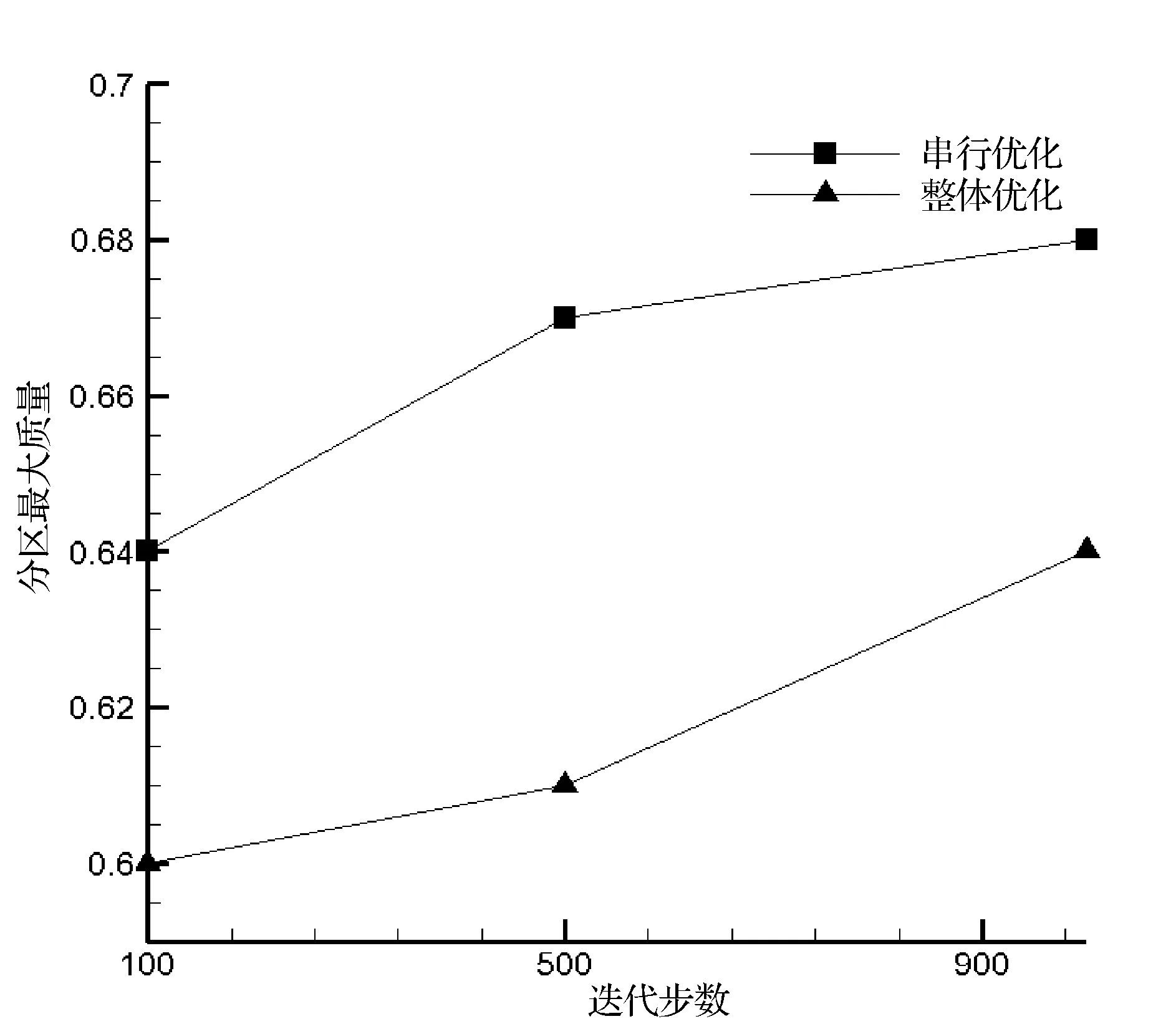
(a) 分区最大质量指标

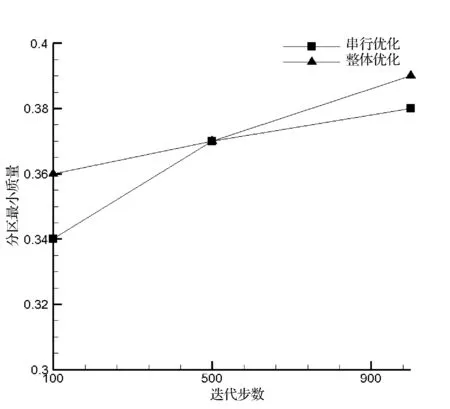
(b) 分区最小质量指标

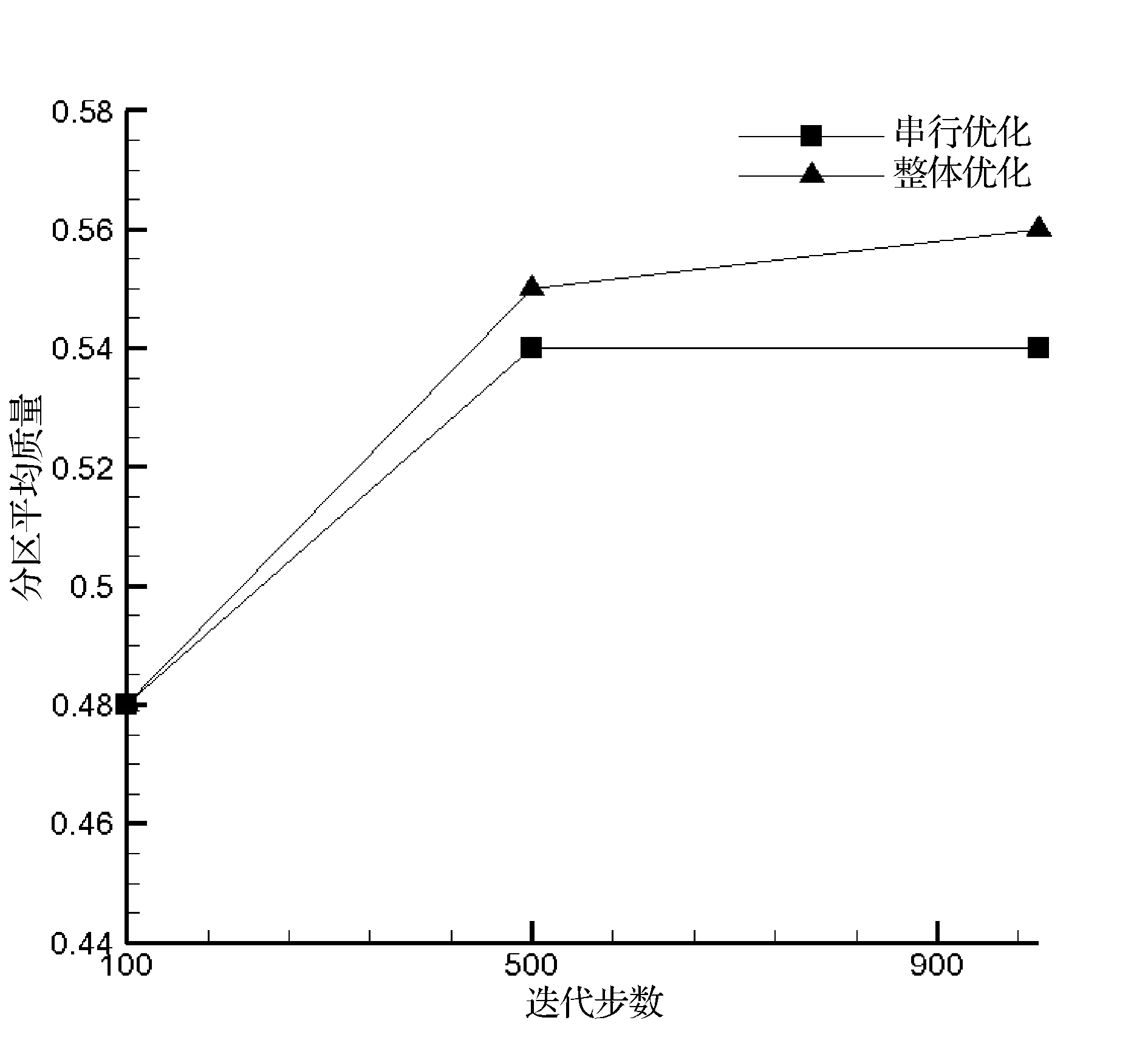
(c) 分区平均质量指标图7 分区质量指标

串行优化算法的目标函数是单个分区的质量指标。在寻优时，每次只考虑一个分区的质量指标，因此此算法得到的分区质量指标最大值更大，且各个分区的质量相差也略大，这也与数据结果一致。整体优化算法的目标函数是所有分区网格质量度量的平均值，因此寻优结果的趋势是使得分区的质量分布较为集中，即各个分区的质量都大致相近。

实验结果表明随着迭代次数的增大，两种优化算法均可提高分区的质量。串行优化算法提高了分区的最大质量，而整体优化算法提高了分区的最小质量及平均质量。在提高分区质量的能力上，整体优化算法更为适用。

由本文设计的一种参数化网格管理软件分别对两种优化方法划分出的分区进行结构化网格划分，并进行网格质量检验，得出的结果如图8所示。(a) 为串行优化分区算法划分出的网格的质量。(b) 为整体优化分区算法划分出的网格的质量。由此可以看出，分区质量越高，网格质量也就越高。

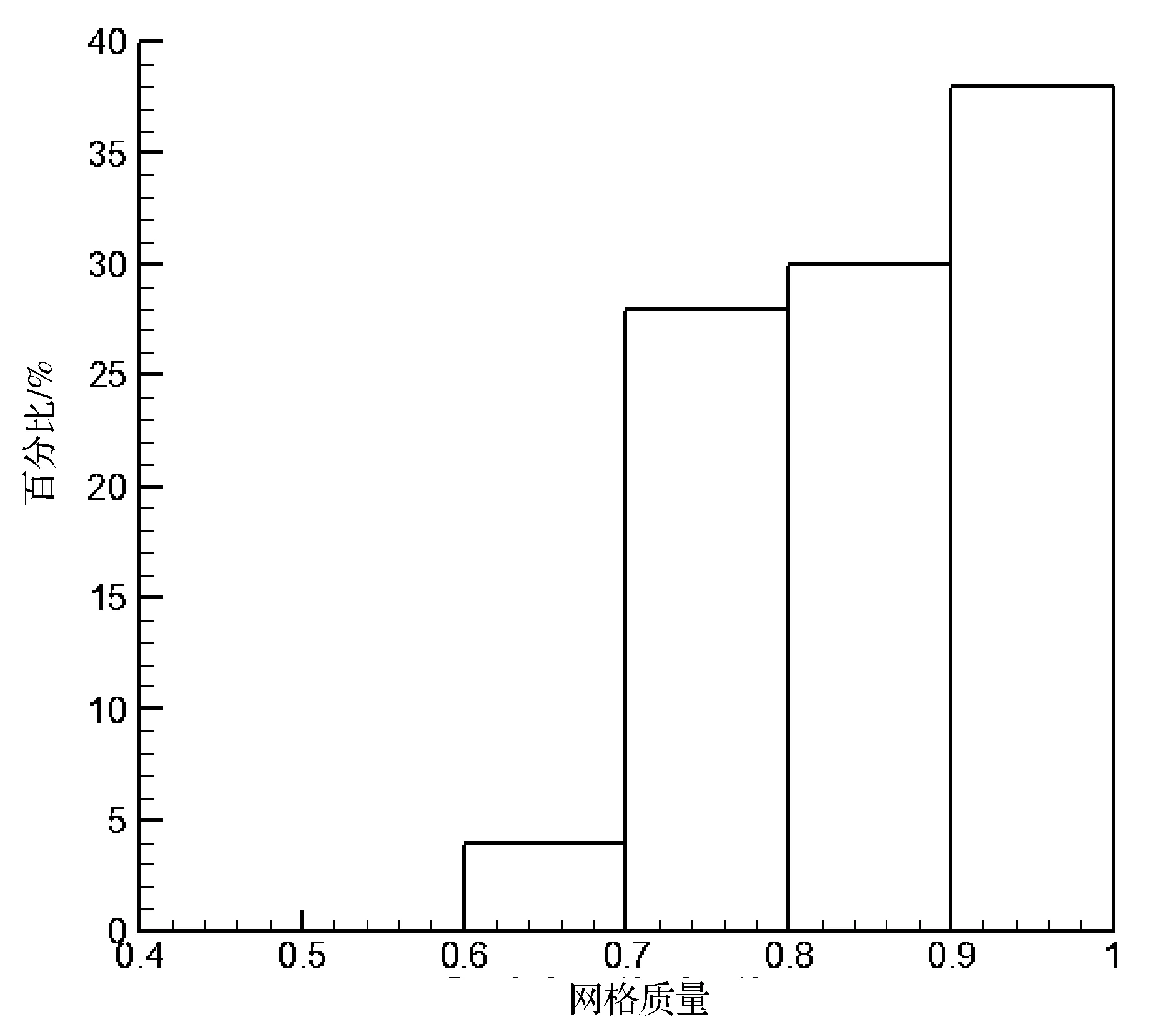
(a) 串行优化分区的网格质量

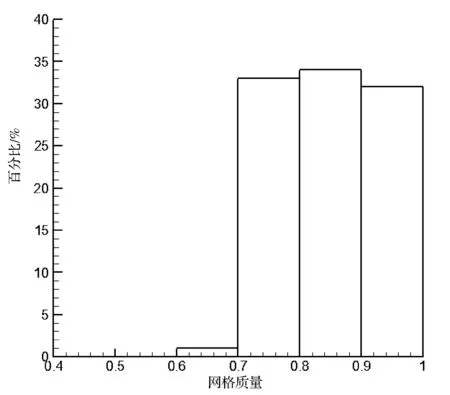
(b) 整体优化的网格分区质量图8 叶盆网格质量

串行优化算法每次单独优化一个分区，寻优完成后再进行第二个分区的优化，因此耗时较长；整体优化算法则同时对所有的分区进行优化，属于多变量寻优，耗时较短。而由人工对此计算域进行分区并优化的过程至少需要两小时。表1为两种优化方法所消耗的时间。实验结果表明随着迭代次数的增加，两种优化算法分区耗时也在增加。而整体优化算法分区耗时普遍比串行优化算法分区耗时短。

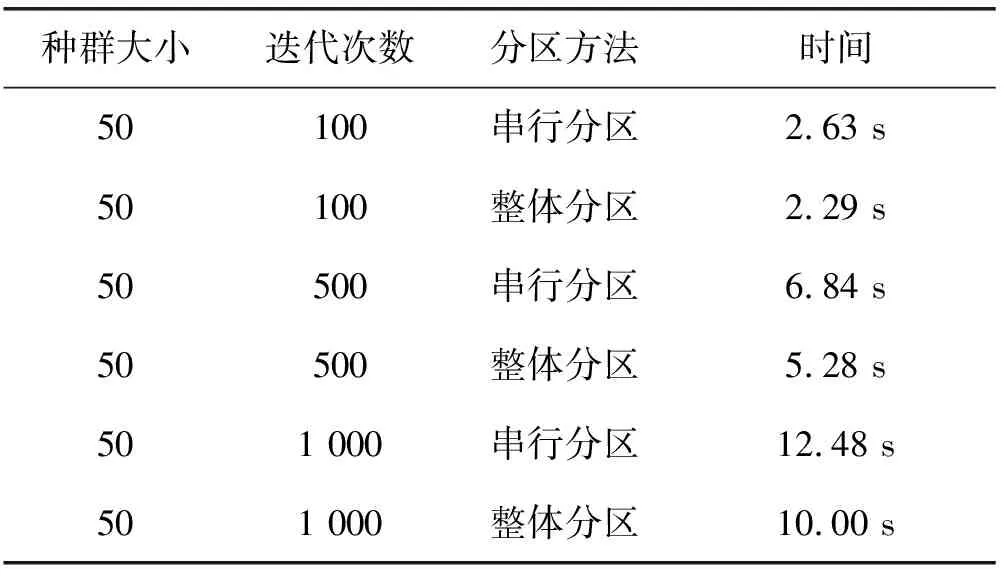
表1 分区耗时

5 结 语

本文对具有复杂边界的几何体的结构化分区优化进行了研究，基于遗传算法提出了两种用于优化网格分区的方法，有效解决了复杂形体结构化分区的自动优化，极大缩短了分区时间。本文通过组合的二进制编码来表述分区切割点的空间位置信息，采用遗传算法将分区的产生构造成一个寻找分区质量最佳的优化过程，从而确定切割点，得到优化分区。其优化过程分为两种，一种是串行优化，即按照顺序依次产生优化分区；另一种是整体优化，使得所有分区的质量平均化。实例验证表明，本文提出的两种自动优化方法可靠，都能够保证高质量网格的生成。而整体优化算法在提高网格质量及计算耗时上更具有优越性。