一种复杂区域层次定性空间推理方法
2018-10-24雒海东宫海彦耿生玲
雒海东 宫海彦 耿生玲*
1(青海师范大学教务处 青海 西宁 810008)2(青海师范大学计算机学院 青海 西宁 810008)
0 引 言
在实际工程应用中,由于精确的定量空间信息难以取得,或者需要的空间信息无需定量精确表示,所以许多重要空间信息都是定性表示和推理的。定性空间推理研究已成为人工智能、地理信息系统(GIS)[1]和机器人导航[2]等领域的研究热点。区域连接演算理论(RCC)[3]是空间区域间拓扑关系模型研究最具有代表性的逻辑方法。空间推理模型目前主要通过对简单区域间的拓扑关系来研究,提出的模型主要有4-交集模型、8-交集模型、9-交集模型、12-交集模型和25-交集模型等[4-9]。在实际应用中,空间区域往往都是复杂区域,仅仅利用简单区域间的关系已经不足以描述复杂区域内部各组成对象间的空间关系。继Worboys等[10]提出一种树模型、Schneider等[11]提出一种成分模型后,Li[12]提出一种图模型,能有效地表示复杂区域内部各组成部分间的空间关系,尤其在机器人避障问题的研究中,但未涉及推理问题。
本文系统地研究复杂区域内各成分间的空间关系图模型,给出一种启发式定性空间推理的方法和应用模型。该方法基于复杂区域内各成分的邻域连接图模型,定义一个邻域层次矩阵,可两两互斥并完备地表示复杂区域中n成分间的连接关系。以3成分的复杂区域为例,利用约束条件[13-14]可得到19种空间层次关系,同时给出一种启发式推理系统。将该方法应用于对机器人与障碍物的层次关系进行模拟,对机器人避障进行建模表示,制定相应的避障方案。
1 复杂区域的邻域连接图模型
Li[12]将平面区域定义为实际平面的正规闭集。对于一个有界平面区域A,称A内部的正闭集为A的正成分,记为A+;称A外部的正闭集为A的负成分,记为A′;称A外部唯一的一个无边界成分的闭包为A的无边界成分,记为b0;称A的外部中每一个有边界的成分为A的洞成分,或简单称为A的洞,记为A-。因此A的每一个成分是一个平面区域,也就是平面中的正规闭集。便于实际应用,一个有界区域存在有限多个正成分和洞。
定义1[12] 一个复杂区域A是一个实际平面的有界正规闭子集,它有有限的正成分和洞,且每个正成分和每个洞都是带洞的简单区域,如图1所示。
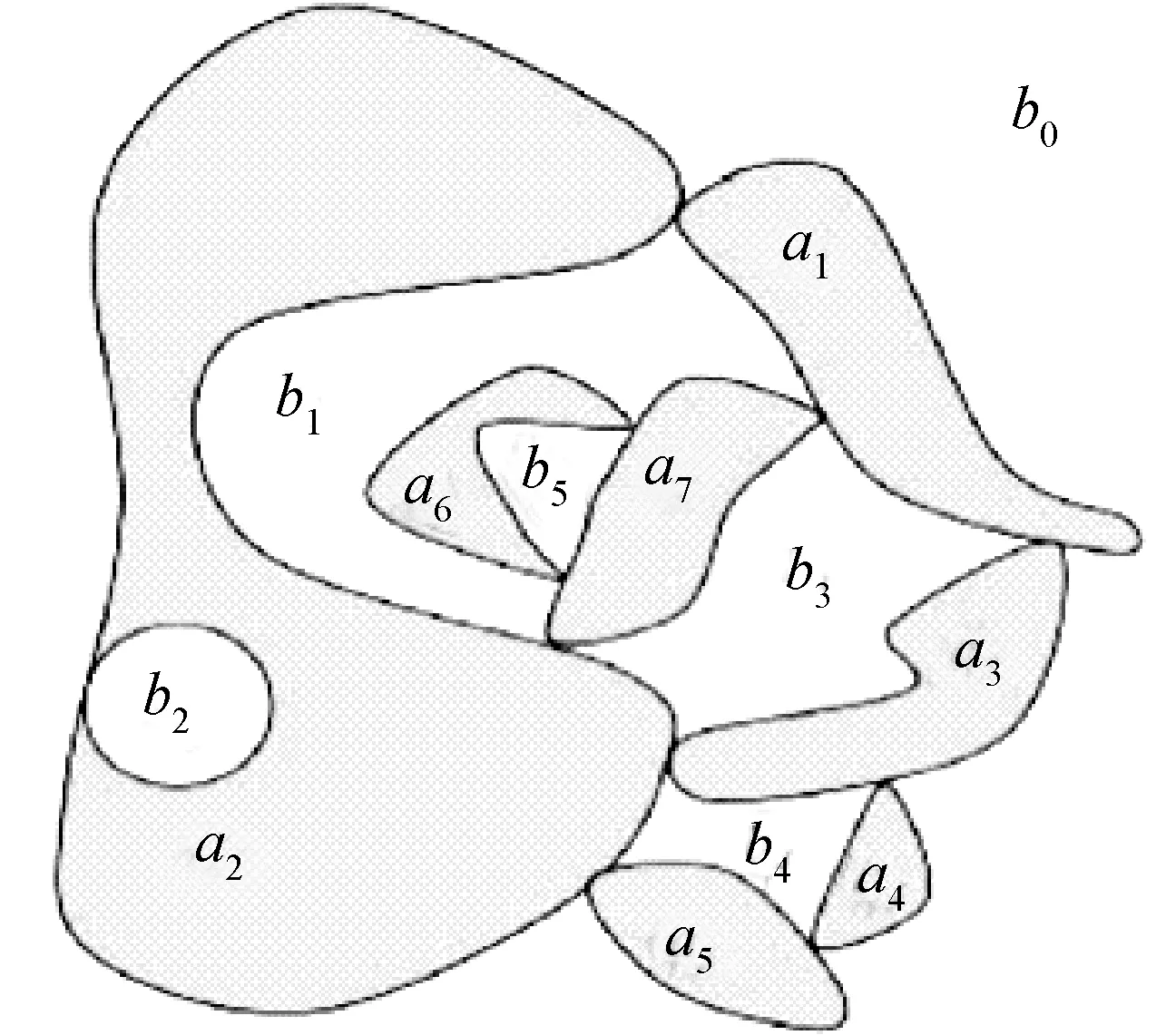
图1 复杂区域A
如果两个成分交集的闭集包含一个简单的曲线,则称两个成分是强连接或者连接的。每个成分至少与其他成分相连接,因为它的边界包含在其他所有成分边界的并集中。
定义2[12] 对于一个复杂区域A,∀C∈A,定义层次函数lev:c→N,存在:
(1) 无边界成分b0∈A,则lev(b0)=0;
(2) ∀b,c∈A, 存在c连接b,则lev(b)=lev(c)+1。
对于两个连接的成分b、c,可知lev(b)-lev(c)=±1。以图1中复杂区域A为例,可知lev(b0)=0、lev(a1)=lev(a2)=lev(a3)=lev(a4)=lev(a5)=1、lev(b1)=lev(b2)=lev(b3)=lev(b4)=2、lev(a6)=lev(a7)=3、lev(b5)=4。



图1中复杂区域A对应的邻域连接图如图2所示。任何一个复杂区域都可以用一个邻域连接图表示。复杂区域的邻域连接图的深度表示为τ(A)=max{lev(ai)∶∀ai∈A,0≤i≤n}。
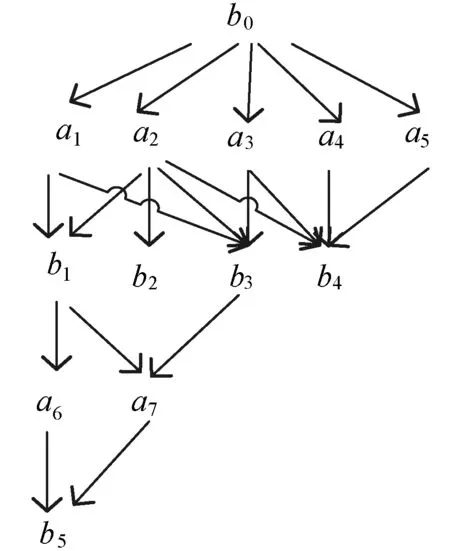
图2 复杂区域A对应的邻域连接图
2 基于邻域连接图的复杂区域定性空间推理
2.1 复杂区域的邻域层次矩阵
为了表示复杂区域内各成分的空间层次关系,在邻域连接图的基础上,建立一个邻域层次矩阵,反映各成分间的层次关系,得到一个n×n的数值矩阵,n表示复杂区域内成分个数。


对于任意的复杂区域就对应了一个邻域层次矩阵。当i=j,xij为ai自身的连接关系,值为0;当i≠j,xij为连接的成分ai和aj之间的层次关系,xji为连接的成分bj和bi之间的层次关系,因此xij和xji互为相反数。这样可得到(2n-1)n(n-1)/2种邻域层次矩阵,每种矩阵对应一种层次关系,但并不是所有的邻域层次矩阵都可实现,如图3和图4所示。
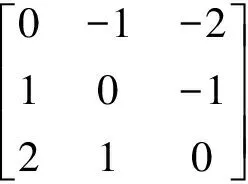
图3 可实现的邻域层次矩阵
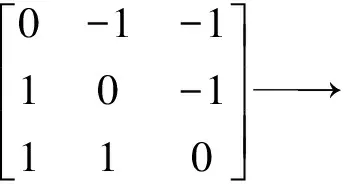
图4 不可实现的邻域层次矩阵
定义复杂区域内两成分对应的邻域层次矩阵ε(a,b),ε(a,b)是一个二阶矩阵可表示为:
ε(a,b)=λL(a,b)
定义5已知二阶邻域层次矩阵εa、εb,定义连接运算∘:
εa∘εb=(λa∘λb)(La+Lb)
式中:λa∘λb∈{0,1}。
定理1邻域层次矩阵是一个主对角线元素为0且对称元素互为相反数的矩阵。
证明:由邻域层次矩阵定义直接可得。
定理2对于复杂区域内成分a与b、b与c、a与c的邻域层次矩阵ε(a,b)、ε(b,c)、ε(a,c),则如下关系成立:
ε(a,c)=ε(a,b)∘ε(b,c)。
证明:由于ε(a,b)=λabL(a,b),ε(b,c)=λbcL(b,c), 则
ε(a,b)∘ε(b,c)=λab∘λbc(L(a,b)+L(b,c))=
得证。
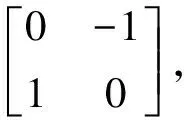
2.2 复杂区域层次定性空间推理
基于邻域层次矩阵的基础上,进行层次定性空间推理,为了得到所有复杂区域成分间可实现的层次关系,加入约束条件,从而去掉不可实现的情形。
引理1对于n成分的复杂区域A, 可递归地得到邻域层次矩阵X, 即X=°i∈[1,n]ε(ai,ai+1)。
证明:由定理2可得。
定理3邻域层次矩阵给出的复杂区域中各成分的层次关系是两两互斥且完备的。
证明:所有的复杂区域邻域连接图都可用一个邻域层次矩阵来表示。因为在邻域层次矩阵中,连接因子反映任意两个成分之间的连接关系,两成分间关系必存在“连接”或“无连接”的情况,并且L(a,b)给出的是邻域连接图中的两节点的层次差,值必属于集合{-(τ-1),…,-1,0,1,…,τ-1}。所以对于复杂区域内任意成分,有且仅有一个邻域层次矩阵对应其在邻域连接图中的层次关系。因此两两互斥且完备。
约束条件1一个复杂区域A含有有限的正成分和洞成分,邻域层次矩阵表示的是有界成分间的空间层次关系,则必须满足:∀a∈A-b0,lev(a)≥1。
约束条件2一个邻域层次矩阵能够对应一个可实现的复杂区域n成分连接空间关系,必须满足:
ε(A,C)=ε(A,B)∘ε(B,C)
对于复杂区域中各成分间的层次关系,在两个约束条件下, 通过算法程序计算可实现的邻域层次矩阵。算法如下:
算法1GetRelation(n)
输入:复杂区域成分个数n,lev= {lev(a1),lev(a2),…,lev(an)};
输出:满足约束条件的邻域层次矩阵集合R。
R=null;
fori=1;i<=n;i++ do
forj=1;j<=n;j++ do
ifi=jthen
xij=0;
ifi≠jthen
ifai连接ajthen
λ=1;
else
λ=0;
X[i,j]=λ(lev(ai)-lev(aj));
for eachε(ai,aj)inXdo
{ifε(ai,aj)满足约束条件1And约束条件2
then
R=R∪X; }
} }}
returnR;
GetRelation(n)算法时间复杂度为O(n3),n表示复杂区域内成分个数。例如,复杂区域中三个成分a、b和c理论上存在53=125种邻域层次矩阵,即125种层次关系。最终运行程序得到可实现的19种连接关系,如图5所示。
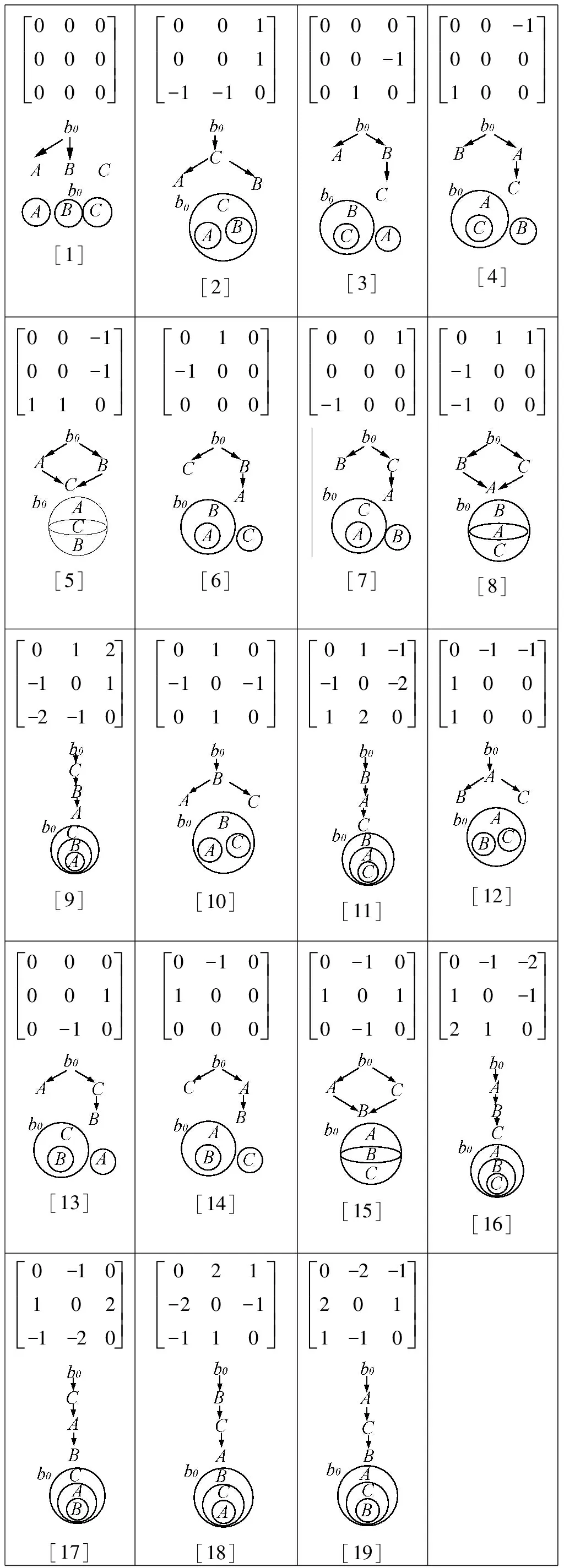
000000000éëêêêùûúúú[1]001001-1-10éëêêêùûúúú[2]00000-1010éëêêêùûúúú[3]00-1000100éëêêêùûúúú[4]00-100-1110éëêêêùûúúú[5]010-100000éëêêêùûúúú[6]001000-100éëêêêùûúúú[7]011-100-100éëêêêùûúúú[8]012-101-2-10éëêêêùûúúú[9]010-10-1010éëêêêùûúúú[10]01-1-10-2120éëêêêùûúúú[11]0-1-1100100éëêêêùûúúú[12]0000010-10éëêêêùûúúú[13]0-10100000éëêêêùûúúú[14]0-101010-10éëêêêùûúúú[15]0-1-210-1210éëêêêùûúúú[16]0-10102-1-20éëêêêùûúúú[17]021-20-1-110éëêêêùûúúú[18]0-2-12011-10éëêêêùûúúú[19]
图5 19种可实现的层次关系
2.3 复杂区域启发式层次定性空间推理算法
通过对上述可实现的邻域层次矩阵的研究,可以对n元层次关系进行启发式的推理,利用算法自动生成复合表,即已知ε(ai,aj)、ε(aj,ak),可自动推理出ε(ai,ak)。条件如下:
ε(ai,ak)=ε(ai,aj)∘ε(aj,ak)
记所有可实现的邻域层次矩阵集合R={Xt;t=1,2,…,(2n-1)n(n-1)/2},遍历R中(ε(ai,aj),ε(aj,ak)的所有可能,对每种情况都按照条件得到ε(ai,ak),除去重复项,则可生成层次关系复合表。算法的伪代码描述如下:
算法2Table_Complex(R)
输入:满足约束条件的邻域层次矩阵集合R;
输出:空间关系复合表tab_com。
tab_com= null;
for eachXinRdo
foreachε(ai,aj),ε(aj,ak)inXdo
{ε(ai,ak) ←ε(ai,aj)∘ε(aj,ak);
tab_com(i, 1) =ε(ai,aj) ∪ε(aj,ak) ∪
ε(ai,ak); }}
returntab_com;
Table_Complex(R)算法时间复杂度为O(n3),n表示复杂区域内成分个数。
3 机器人动态避障应用实例与分析
3.1 应用实例
文献[15]利用简单区域的8-交集模型对机器人和两障碍物的避障进行推理模拟。本文所建立的基于邻域连接图的复杂区域定性空间推理方法,可用于对复杂区域中机器人与两个指定障碍物的层次关系进行模拟。在层次关系推理方法的建立中,假定区域对象C为机器人,区域对象A、B为障碍物。为此本文建立的实验环境:X2BOT轮式机器人开发平台, 配置为四核2.7 GHz主控制器, Windows 7操作系统。图6是机器人避障仿真系统,在此基础上将层次定性空间推理方法运用于机器人避障预测模拟系统中。机器人避障利用声纳避障,图6中机器人有5个声纳传感器分别探测不同方向上机器人与障碍物的距离,1号传感器位于机身的左侧,2号传感器位于机身的右侧,3~5号传感器从左到右依次分布于机身的前方。图7表示5个声纳传感器在机器人运行时的数值变化。随着时间的增加,机器人和障碍物的距离逐渐缩短,5个传感器的数值随之减少。
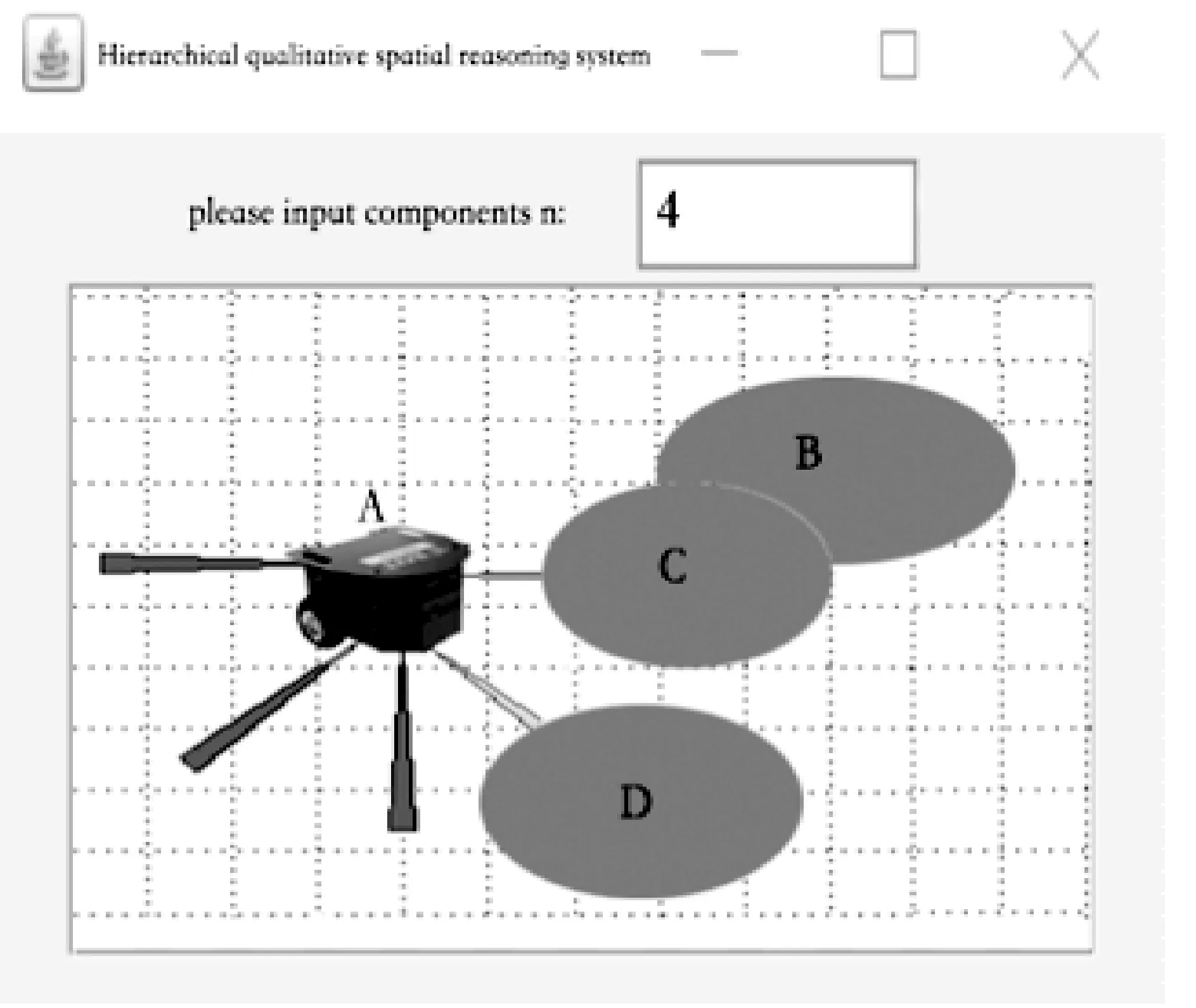
图6 机器人避障仿真系统
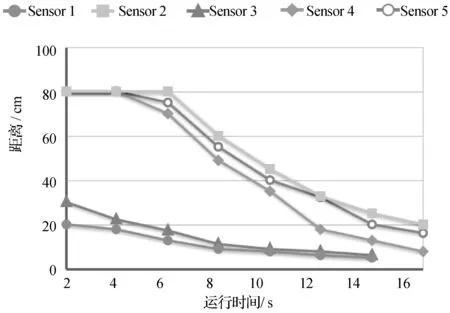
图7 声纳值变化
如果能对机器人C与障碍物A、障碍物B间的层次关系进行预测和表示,机器人就能够躲避障碍物运动,减少碰撞过程中的损失。根据上述层次关系推理方法可知,由障碍物A与障碍物B在邻域连接图中的层次关系和机器人C与任一障碍物在邻域连接图中的层次关系,可以推理得到机器人C与另一障碍物在邻域连接图中的层次关系,从而改进机器人避障方案。将机器人C与障碍物A、障碍物B的碰撞情况分为如下4种:
(1) 机器人C与障碍物A发生碰撞,但与障碍物B不发生碰撞;
(2) 机器人C与障碍物B发生碰撞,但与障碍物A不发生碰撞;
(3) 机器人C与障碍物A、B均发生碰撞;
(4) 机器人C与障碍物A、B均不发生碰撞。
3.2 实验分析
通过算法1模拟复杂区域中机器人与障碍物间的碰撞情形,与复杂区域中三个成分间的19种层次关系相互对应,再执行算法2,经过推理得出二元层次关系复合表,如表1所示。

表1 二元层次关系复合表
图8给出其中4种情况(图下方的序号分别对应图5中序号)。序号[3]表示机器人C与障碍物B发生碰撞,与障碍物A不发生碰撞;序号[6]表示机器人C与障碍物A、障碍物B均不发生碰撞;序号[7]表示机器人C与障碍物A发生碰撞,与障碍物B不发生碰撞;序号[16]表示机器人C与障碍物A、B均发生碰撞。
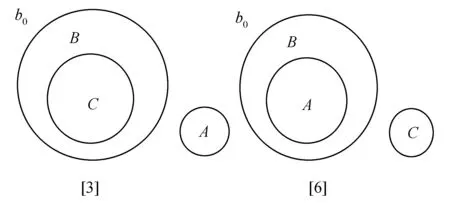
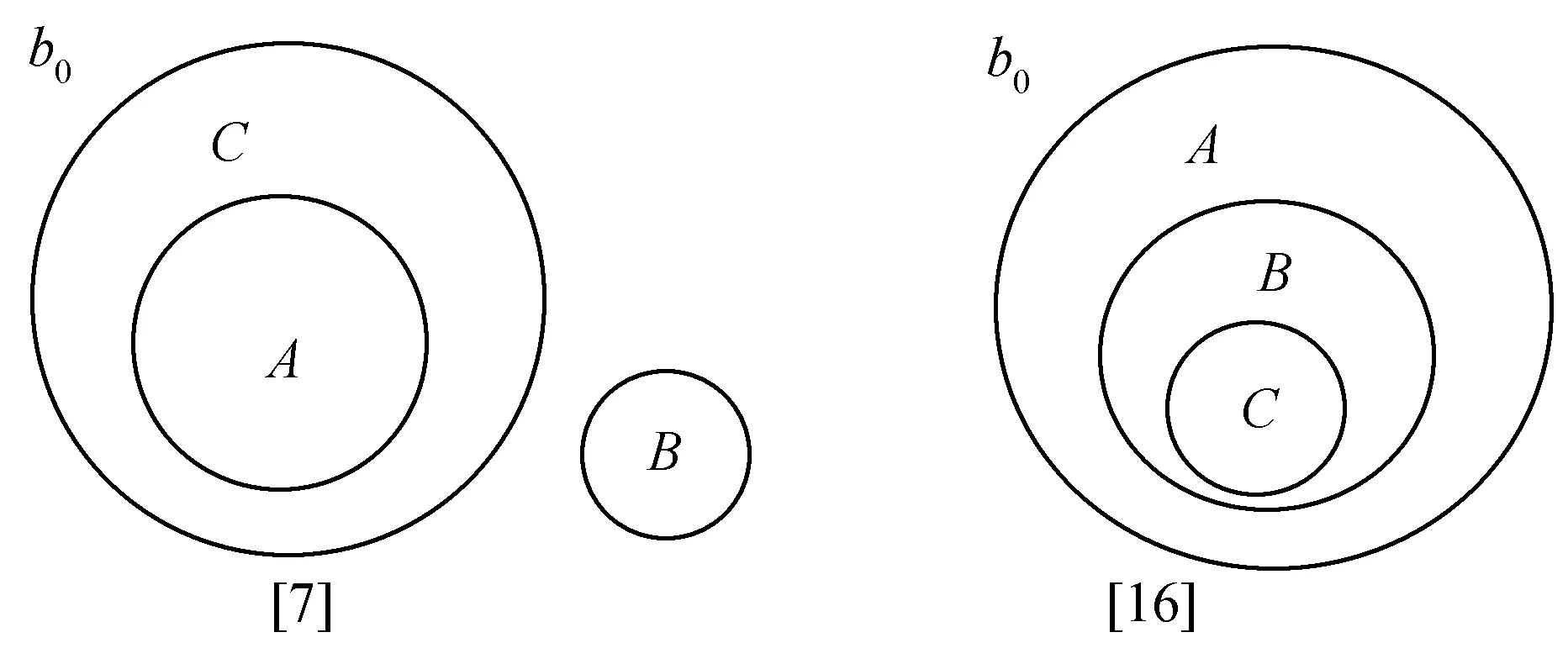
图8 推理三成分间的空间关系
表1中对应的序号[1]、[6]、[14]分别表示这种情形,共有3种情况。本文认为碰撞情形是完全随机的,故其概率为3/19=15.79%,以此类推,机器人C与障碍物A发生碰撞,与障碍物B不发生碰撞的概率为3/19=15.79%;机器人C与障碍物B发生碰撞,与障碍物A不发生碰撞的概率为3/19=15.79%;机器人C与障碍物A、B均发生碰撞的概率为10/19=52.63%。
从模型的运行时间和准确性分析得出,复杂区域内成分的数量是影响算法的主要因素。本文的层次定性空间推理方法采用随机设置障碍物的方式, 通过对机器人避障预测,实现更高效地避障策略, 将该模型与传统避障策略相比较,图9给出成分数量对两种模型运行时间的影响。当成分数量从10到80发生变化时, 可以看出, 层次空间推理模型优于传统避障策略。

图9 不同成分数量下算法运行时间的比较
图10给出成分数量对模型准确性的影响。随着成分数量n的增加, 模型的准确率越来越差, 这是由于成分数量的增加, 会增加算法时间复杂度, 导致可实现邻域层次矩阵的增多, 同时也增加生成复合表的复杂性。
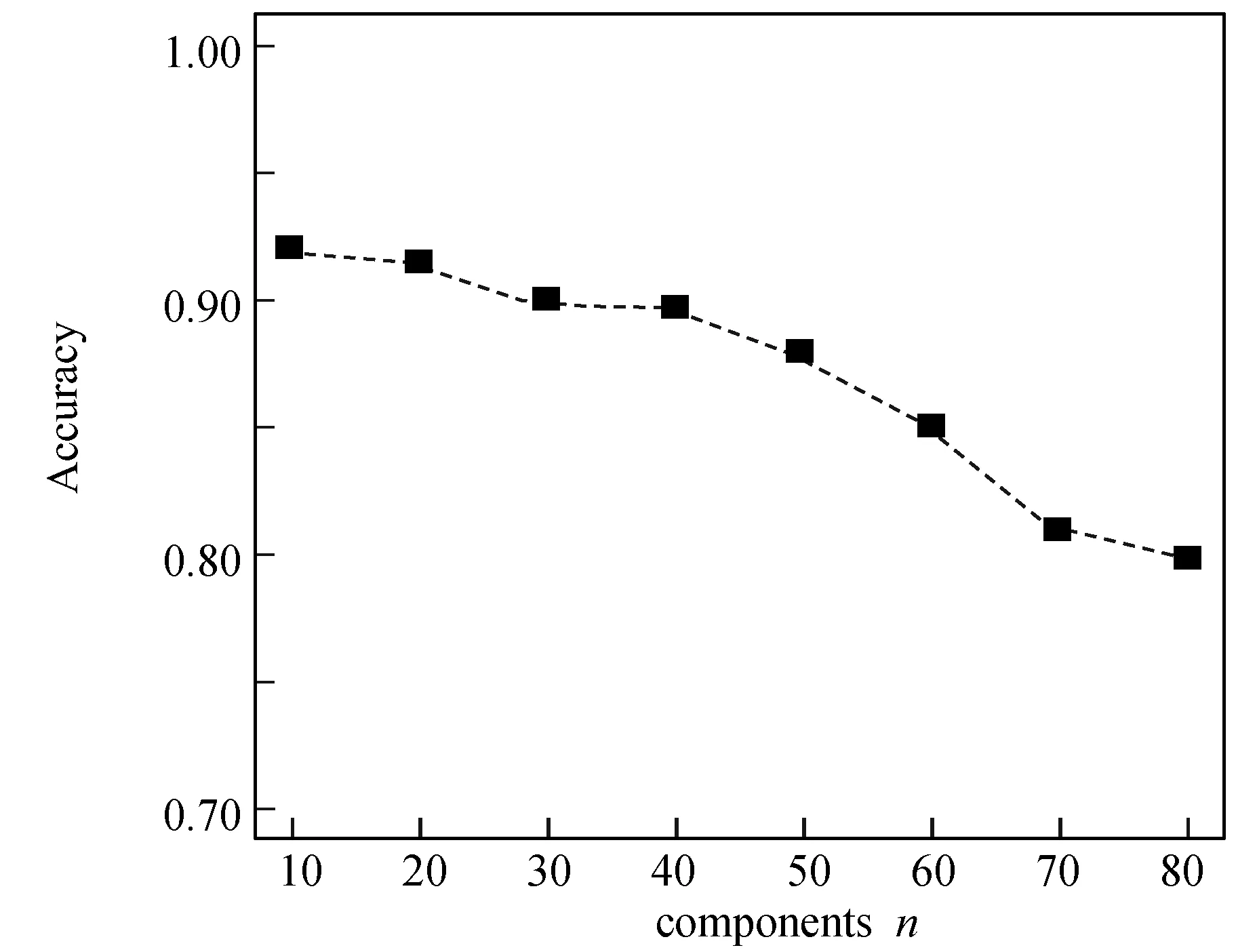
图10 成分数量n对模型准确性的影响
将本文提出的层次定性空间推理模型与8-交集模型[15]的表达能力相比较, 可得出:
(1) 邻域层次矩阵在表达3个区域间关系时可得到可实现的19种空间关系,而8-交集模型在表达3个区域间关系时得到109种三元拓扑关系。比较而言,邻域层次矩阵模型可极大地降低搜索空间,尤其当n较大时。
(2) 8-交集模型在此机器人避障模型中给出25种避障策略选择,表1中可看出邻域层次矩阵模型给出13种避障策略选择, 精减了策略选择范畴,减少算法运行时间,提高运行效率。
总之,邻域层次矩阵模型适合表示复杂区域内多个区域间空间关系和推理,而8-交集模型只适合表示3个简单区域间空间关系和推理。比较而言, 邻域层次矩阵模型表达范围更广。
4 结 语
本文在复杂区域邻域连接图表示方法的基础上,定义了邻域层次矩阵。并根据约束条件,通过算法程序计算得到可实现的邻域层次矩阵,通过邻域层次矩阵,利用二元层次关系对多成分间的空间关系进行启发式推理。将本文所提出的基于层次关系的复杂区域定性空间推理方法应用于模拟机器人避障情形,并制定相应避障策略。
复杂区域内空间关系十分复杂,层次关系表示和推理是一种近似方法,还需考虑很多细节。因此,研究如何对复杂区域内空间关系定性推理和精准的定量方法结合,提高控制或决策的准确性和效率是接下来的研究重点。
