GMR生物传感器专用信号检测电路系统设计
2018-10-24文枰
文 枰
(四川文理学院智能制造学院 四川 达州 635000)
0 引 言
GMR生物传感器主要由GMR传感芯片和信号检测电路组成[1-3],它的直接检测对象是与待测生物分子结合的免疫磁珠[4-5]。GMR传感芯片内部由阻值在几百欧姆至几千欧姆的GMR磁阻条构成惠斯通电桥结构。利用磁珠磁场引起的敏感电阻改变,来实现目标生物分子的检测[6-7]。由于免疫磁珠的体积很小(粒径为纳米至微米量级),其被磁化后产生的附加磁场强度也极小,使得GMR芯片的输出有效信号十分微弱(信号的幅值与施加的激励磁场和免疫磁珠有关,通常在微伏级),且常常被湮没在工频噪声及其谐波、激发信号及其谐波等强背景噪声中,造成信噪比很低。因此,仅仅通过放大、滤波等常用的检测方法不能满足要求。另外,对于GMR生物传感器来说,要求信号检测具有一定的快速性和实时性。
锁相放大是微弱信号检测的重要方法[8-10]。虽然可以采用商用锁相放大器对GMR生物传感器的输出信号进行检测,但是商用锁相放大器存在着体积大、价格昂贵等缺点,不利于GMR生物传感器的集成化和微型化,难以满足现场快速检测的需求。可见,设计GMR生物传感器专用信号检测电路十分必要。
基于FPGA技术的数字电路具有稳定性好、抗干扰能力强、处理速度快、体积小、可灵活定制等诸多优势。因此,本文根据GMR生物传感器输出信号的特点,设计了一套基于FPGA的数字式微弱信号相关检测电路系统。还设计了DDS、幅度检测等核心模块,并对系统进行了联合调试和测试。
1 双通道相关检测的原理
GMR生物传感器的输出信号频率等于外加激励磁场的频率(本电路以频率为2 kHz的激励磁场信号为准而设计),因此,本文采用双通道互相关检测技术[11]。如图1所示,其核心为相关检测器,主要由相敏检测器(PSD)和低通滤波器(LPF)组成。
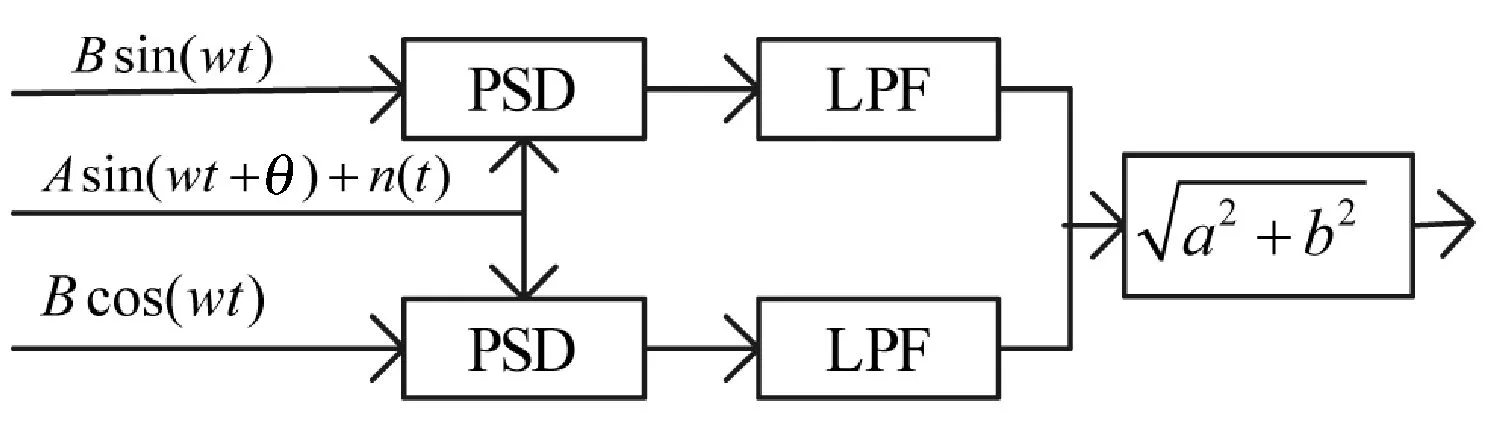
图1 双通道相关检测原理图
图1中,Asin(ωt+θ)+n(t)为被测信号,由有用信号Asin(ωt+θ)和随机噪声n(t)组成。Bsin(ωt)和Bcos(ωt)为一对正交的参考信号。
被测信号分别与正交参考信号Bsin(ωt)和Bcos(ωt)进行互相关运算,即经过相敏检测器和低通滤波器(这里采用积分器实现低通滤波)之后,第一路的运算结果为:
n(t)]Bsin(ωt)dt=(ABcosθ)/2
(1)
第二路的运算结果为:
n(t)]Bcos(ωt)dt=(ABsinθ)/2
(2)
再将两路运算结果求均方根,且当参考信号的幅度为1时,即当B=1,可以直接得出被测信号的幅值:
(3)
由式(3)可知,采用双通道相关检测,可极大地抑制背景噪声,且不受参考信号与待测信号相位差θ波动的影响,具有很高的信噪比和稳定性。
2 系统设计
整个电路系统框图如图2所示,包括前端信号调理、A/D转换、FPGA数字处理。图中虚线框内表示FPGA内部信号处理部分。

图2 系统结构原理图
2.1 信号调理及A/D转换
信号调理电路包括放大电路和带通滤波电路。采用两级放大:第一级采用仪表放大器芯片AD8429实现,设计放大倍数为501倍;第二级采用OP27构成同相放大,放大倍数为4倍。采用AD公司生产的ADA4851-1芯片设计二阶有源带通滤波器,滤波器的中心频率为2 kHz,通频带宽为200 Hz,通带增益为20 dB。电路原理图如图3所示。A/D转换电路用MAXIM公司生产的16位A/D转换器MAX1179芯片实现。
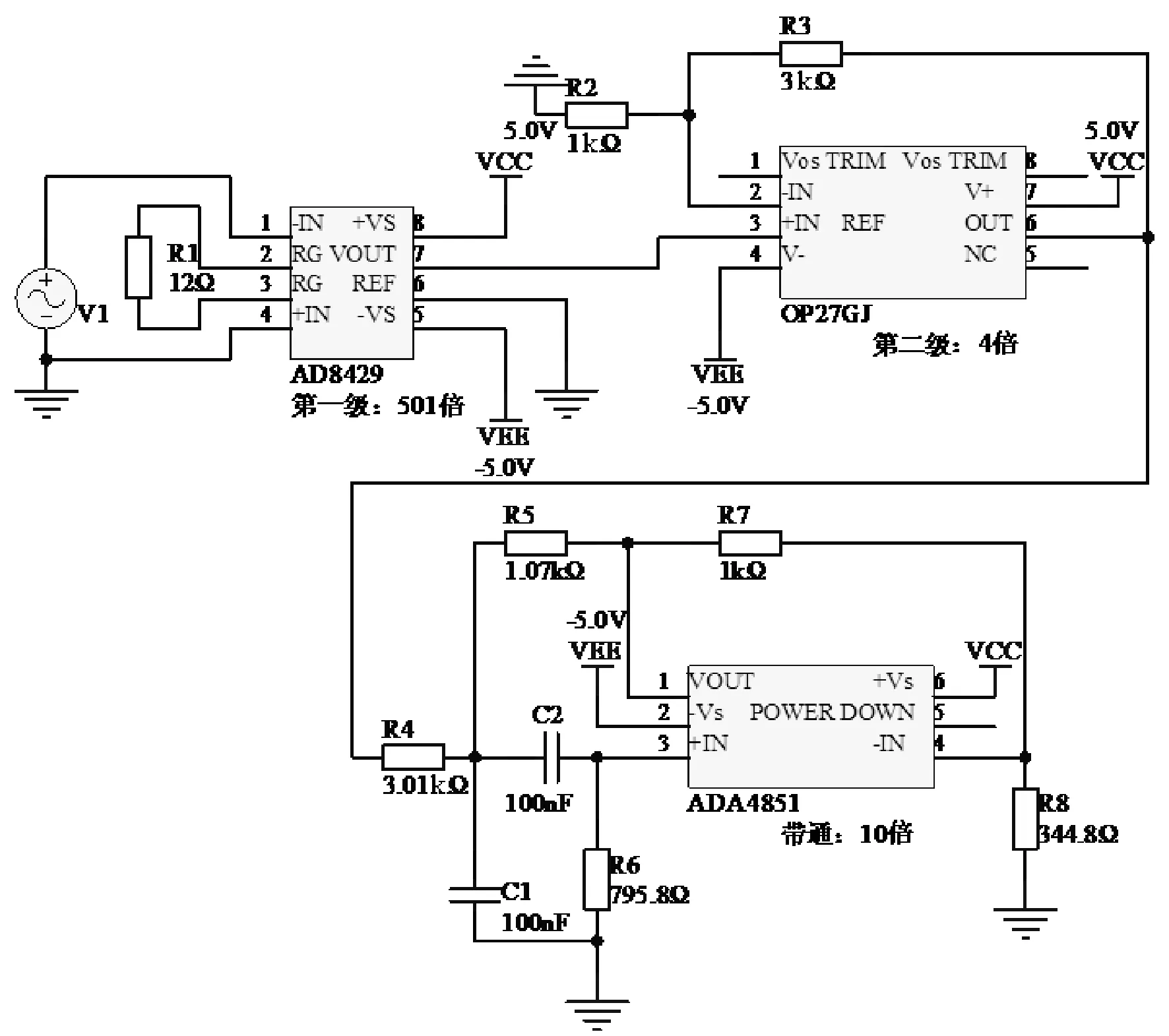
图3 电路原理图
2.2 数字信号处理关键模块
FPGA内部信号处理部分主要包括带通滤波、DDS、相敏检测、低通滤波、幅值求解等模块[12-14]。模块代码均采用Verilog HDL编写。为了提高信号处理的速度,所有模块采用流水线结构编写代码。
2.2.1 数字滤波器
本文采用分布式算法设计FIR滤波器。带通滤波器和低通滤波器均设计为64阶的分布式算法滤波器。
设长度为M×N的内积为:
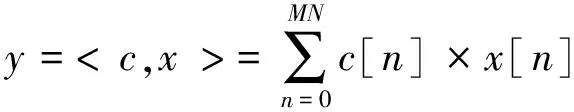
(4)
将式(4)中的乘积和分割成M个独立的N阶并行查找表,可得:
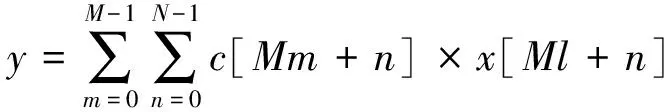
(5)
将64输入的查找表分为8个并行的8输入查找表。图4为数字低通滤波器的仿真结果。
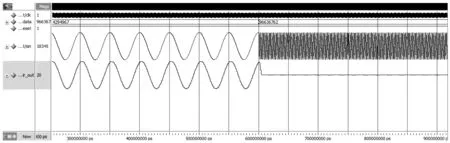
图4 低通滤波器仿真结果
可见,频率在通带内的信号几乎无衰减地通过低通滤波器,而带外信号被有效地滤除。
2.2.2DDS信号源
DDS模块的输出频率fout是系统时钟频率fclk、相位累加器的位数N和频率控制字K的函数,数学关系式为:
(6)
显然N越大,频率分辨率越高。综合考虑输出频率分辨率和ROM查找表的容量消耗,DDS中的相位累加器和频率控制字的位宽均取32位,ROM查找表的地址位宽取10位。系统时钟频率为20 MHz,要得到频率为2 kHz的正交参考信号,依据数学关系式可得频率控制字(取整):K=429 497。采用ModelSim软件仿真结果如图5所示,由图可知,能够准确的产生两路正交的参考信号,频率均为2 kHz。
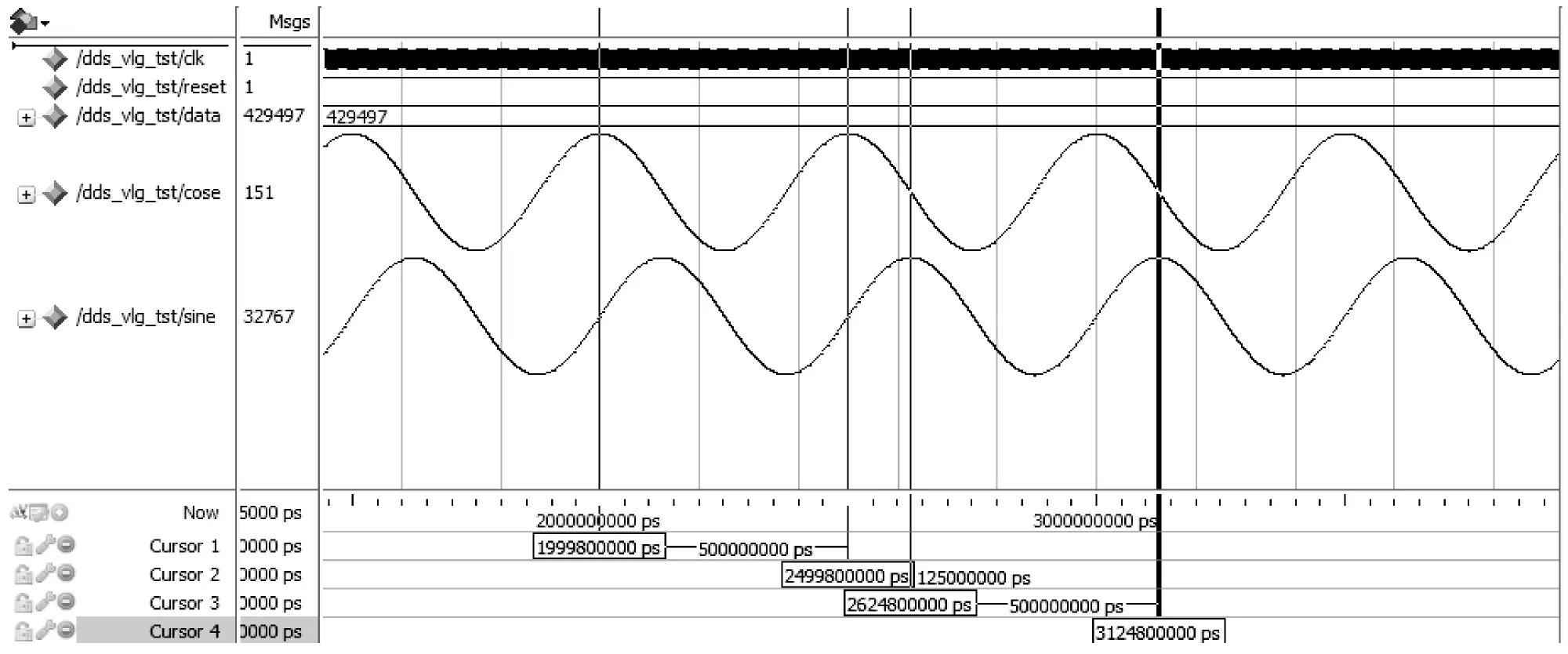
图5 DDS仿真结果
2.2.3 信号幅值求解
采用CORDIC算法的向量模式来计算被测正弦信号的幅值。设A为需要旋转的角度,当旋转到与x轴重合时,Y变为0,算法原理如下:
Xn+1=Xn-SnYn2-n
(7)
Yn+1=Yn-SnXn2-n
(8)
An+1=An-Snarctan(2-n)
(9)
经过N次迭代过后,公式变为:
(10)
Yn+1=0
(11)
(12)
式中:
(13)
如果A0=0,对于给定的X0和Y0,经过N次迭代后CORDIC算法的输出公式变为:
(14)
将相关器输出的两路信号分别代入式(14)的X和Y,即可计算出向量(X,Y)的长度,即待测信号的幅值。
综合精度要求与FPGA内部资源消耗情况,采用七级迭代CORDIC算法实现信号幅值求解。仿真结果如图6所示。仿真结果与理论计算相符。
图6 幅值求解模块仿真结果
2.2.4 系统仿真
将各个模块级联,进行系统仿真。仿真结果如图7所示。可见,被测信号进入相关检测系统后,经过一定时间后稳定为直流输出。输出数字量的范围为16 352~16 379,经计算,相对误差低于0.2%。
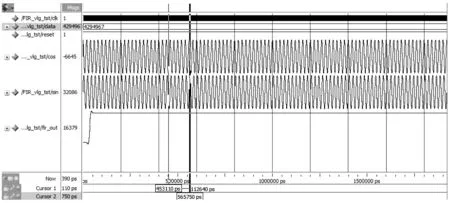
图7 系统仿真结果
3 实验结果及性能分析
为了检验设计的检测电路系统的性能,对该电路进行了测试,测试平台如图8所示。采用美国安捷伦公司的Agilent-Keysight33621A函数信号发生器产生正弦信号,并使用精密金属膜电阻进行100∶1分压,从而获得微伏量级的待测信号。

图8 电路测试平台
表1为输入信号幅值分别为10、20、50、100 μV时的实验测试结果。由测试结果可知,当输入信号为10 μV时,检测的相对误差比较大。随着输入信号幅值的增大,检测的相对误差呈减小趋势。经分析,产生误差的主要原因有:信号调理电路的增益漂移、A/D转换的量化误差和FPGA内部信号处理的误差。
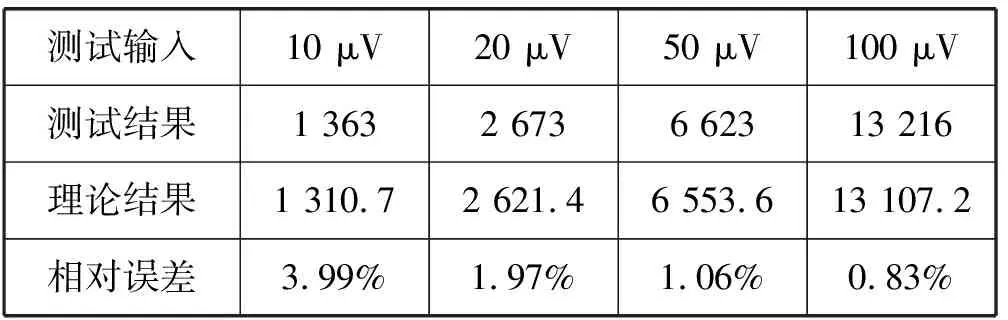
表1 实验测试结果
4 结 语
针对GMR生物传感器输出微弱信号检测问题,设计了GMR生物传感器专用的数字化信号检测电路,对电路关键模块进行了分析,完成了检测电路设计。测试实验表明,该电路能有效地将微弱信号检测出来,且检测的相对误差随着被测信号幅值的增大而逐渐减小,当输入信号为100 μV时,检测相对误差为0.83%。实验结果证明了该电路具有良好的弱信号检测性能,为GMR生物传感器检测系统的集成化和小型化奠定了一定基础。
