考虑客户满意度的配送时隙替代定价策略

朱恒恒 陈淮莉

(上海海事大学物流研究中心 上海 201306)

0 引 言

网络零售配送是电子商务B2C模式中重要的一个环节，为了降低配送成本，提高配送的效率和服务的质量，国内外学者对配送时间窗即时隙的选择和定价问题进行了多项研究。时隙(time slot)是指电子商务B2C模式下网络零售商提供给客户选择的订单产品最终送达的时间窗口[1-2]，对于多数网络零售商来讲，按时履约已经成为交易中重要的组成环节。如Best buy、Tesco、京东和菜鸟联盟等均提供多个时隙以供客户选择。客户根据自身需求选择时间段等待货物交付。提供多种可选择的配送时隙选项并满足客户满意度需求，可以使得客户流失率降低，使客户可以进行更多的时隙替代性选择。这也为网络零售商配送增加了难度，不仅要考虑到按时履行订单获取盈利，还要在考虑到客户满意度的同时对多个相互可替代配送时隙选项之间进行价格的调整，以实现目标收益的最大化，是现在网络零售商所面临的具有挑战性的管理问题。

国内外在研究时隙方面的文献相对较少，多数集中在决策优化和物流配送路径两个方面，如Rintamäki等[3]通过参照与其竞争优势相关的特定环境来衡量和建模客户价值感知，给出了一个衡量和建模客户价值的量表的开发和验证，并提供了如何有助于客户价值命题的评价视角。文献[4]等人的研究中通过接受尽可能多的送货请求，制定和比较策略，最大限度地提高物流服务提供商的利润，并评估客户请求对送货旅游服务质量的潜在影响。同时，引入了多种接受机制，通过建立启发的模拟框架，比较接受机制的利润和服务质量，但没有考虑到客户的主动选择和时隙替代行为。Punakivi[5]在其研究中比较了有人和无人值守两种不同情况下物流送货过程所需的总成本，对比分析了配送时间窗长度这一因素的影响，表明较为宽泛的时间窗能够提升工作效率。在两个小时的服务时间窗内，通过对比发现无人值守的服务成本相较于有人值守要降低1/3。文献[6]提出了一种新的通过送货时隙定价来控制需求的方法，通过将整个交付问题分解为一系列较小的、特定区域的问题用动态规划方法来估计交付成本。利用行业大数据，建立多项Logit模型客户选择模型，结果显示，相对于在电子商务中常见的固定价格策略，此方法能够提高超过2%的利润。文献[7]采取Markov链中差异化定价的方法来激励客户的选择行为，结论显示在提高效用和客户抵达率的过程中，时隙的定价也相应地提高，而提高交付期则使得时隙价格降低。Robusté[8]的研究通过对时隙的连续逼近来分析对交付效率的影响，证明了在配送能力不断增加的情况下时隙宽度会得到增大的情况。陈淮莉等在研究中为实现各个时隙选项最大程度的利用，通过不定次调价的方式来引导客户的时隙选择行为，提供了合理的定价方法。李景瑜等[9]在时隙预定过程中引入超售概念，通过对比分析不同属性的客户群体，使得时隙成本降低，提高服务总收益。然而现有的研究中，较少地对网络零售商因时隙配送能力不足而关闭时隙选择时的情况进行考虑，且没有考虑到客户满意程度对时隙替代选择行为的影响。

已有研究表明：满足客户的需求，使得客户的满意度提高可以提升企业的形象，降低企业的宣传成本，提高客户的忠诚度，使得企业能够长久的发展，带来持续的利润。在现实决策中，客户的替代时隙选择行为是不可避免[10]。

本文基于客户离散选择模型，在时隙定价过程中考虑客户满意度和客户时隙替代选择行为两个因素，根据网络零售商对上述两个因素的不同收益偏好对时隙定价策略进行研究。提出了基于客户满意度和期望收益的双重目标下的时隙定价模型，分别讨论了在不同收益偏好和不同时隙交付期下的时隙最佳定价策略，并与仅考虑期望最佳收益下的时隙定价策略进行目标契合度对比，为B2C配送模式下时隙的定价策略提出了一种合理的方案。

1 问题描述与假设

选择时隙配送服务的客户群体可以大致分为两类：价格敏感型和交付期敏感型[11]。

客户在实际选择过程中会根据自身效益最大的原则对不同的配送时隙进行选择，通常希望以较低的价格选择交付期更短的时隙进行配送服务。网络零售商由于目标需求不同，通常会考虑满足客户购买意愿和自身期望收益两个目标，称网络零售商对客户满意度和期望收益有不同的收益偏好。为了简化模型，现进行如下假设：

(1) 客户选择行为符合Logit选择模型。

(2) 当客户由于初选时隙(原时隙)配送能力不足而选择替代时隙时，仅有一次选择机会，若替代时隙的配送能力不足，则不进行第二次时隙替代，时隙预定过程结束。

(3) 时隙i的提前预定期为[0,T]，区间内包含T个时段，假设每个时段充分小，满足在单个时间段内有且仅有一个客户订单抵达，单个时段内的客户订单抵达率满足Poisson分布。

通过上述假设建立双重目标模型：

maxY|Y=ζQ′+(1-ζ)Γ′

(1)

式中：Y表示目标契合程度，Q′定义为无量纲化的期望收益；Γ′定义为无量纲化的客户满意度；ζ定义为网络零售商对期望收益的偏好程度。根据网络零售商不通过的目标需求制定时隙价格使得期望收益和满意度更符合目标要求。

2 模型构建

2.1 客户Logit选择模型

假设Ui为客户对时隙i的预估效用(时隙i的受欢迎程度)[12]，U0为当客户不选择时隙时，客户的预估效用；ui表示时隙i对客户的实际效用；β表示客户选择行为对时隙价格的敏感系数，且β>0；η表示客户选择行为对时隙宽度的敏感系数，η>0；γ表示客户选择行为对时隙宽度的敏感系数，γ>0；wi表示时隙i的宽度；Li表示交付期长度；εi表示反应客户独特偏好的随机变量，服从同一分布的二重最大指数分布；客户总是希望以最低的价格和最快的速度准确送达，所以在公式中反映为当价格、时隙交付期和时隙宽度增大时，客户的实际效用将减少。

ui=Ui-βri-ηwi-γLi+εi∀i∈N

(2)

uo=U0+ε0

(3)

假设时隙i的售价为ri，则此时客户选择它的概率[13]为:

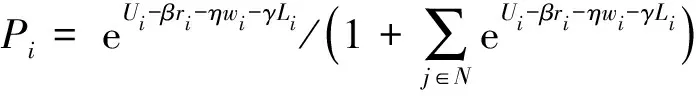
(4)

客户不选择时隙的概率为：

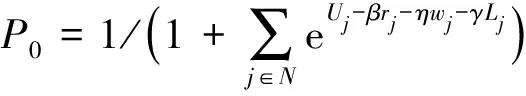
(5)

且有：

(6)

时隙1、时隙2的选择替代关系可表示为：

(7)

式中：当时隙j没有配送能力时,xj=0；其他情况，xj=1；θji表示当时隙j无服务能力时，客户替代选取时隙i的比例[13]。

在整个时隙预定阶段时隙i的需求可表示为：

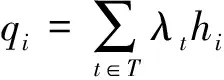
(8)

2.2 收益目标模型

假设时隙i的单位订单成本分为固定成本和可变动成本[12]，有：

Ci=Cf+Cvi

(9)

式中:Ci为单位成本；Cf为固定成本；Cvi为可变成本。

时隙i被客户选择时的可变成本与客户配送路程、时隙交付期长度和宽度有关，且越精确的交付期和时隙宽度对交货的要求越高，相应的可变成本就会越大，在公式中体现为可变成本与配送路程成正比，与时隙交付期和时隙宽度成反比，即：

(10)

式中：dm表示第m个客户的配送路程；α为交付期长度的成本弹性系数；ρ为时隙宽度的成本弹性系数；a表示单位运输成本。

本文在假设仅有两个时隙存在的情况下将收益目标模型分为客户不考虑时隙替代和考虑时隙替代两种情况，时隙2关闭时由时隙1替代。

(1) 不考虑时隙替代的情况：

假设可供客户选择的时隙1、时隙2两个选项在第n个配送订单抵达时状态均为可用[14]。则网络零售商的期望收益为：

V(S1,S2,n)= max{q1[r1+f-C1+V(S1-1,S2,n-1)]+

q2[r2+f-C2+V(S1,S2-1,n-1)]+

q0V(S1,S2,n-1)}

(11)

(2) 考虑时隙替代的情况：

当订单抵达时，时隙1、时隙2中仅有一个时隙关闭，则客户选择另一个。假定时隙2因服务能力不足而关闭，此时客户仅有时隙1一个替代选项，即当S1>0、S2=0、n>1时，得到网络零售商的期望收益函数为：

V(S1,0,n)= max{q1[r1+f-C1+V(S1-1,0,n-1)]+

q0V(S1,0,n-1)}

(12)

式中:S1、S2分别表示时隙1、时隙2的配送能力，即能够服务的订单量。

定理1网络零售商期望收益函数为时隙价格(r1,r2)的凹函数[9]。

证明：令π表示期望收益函数，有：

π(S1,S2,n)=q1[r1+f-C1+V(S1-1,S2,n-1)]+

q2[r2+f-C2+V(S1,S2-1,n-1)]+

q0V(S1,S2,n-1)

(13)

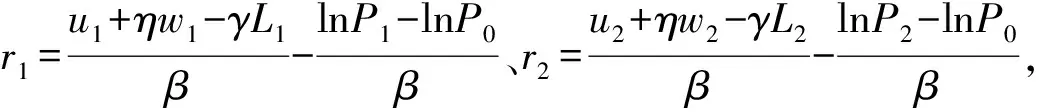
代入原式为：

q0V(S1,S2,n-1)

(14)

对π(S1,S2,n)关于P1和P2求一阶、二阶导数，有：

(15)

(16)

(17)

(18)

则ad-bc>0,因此有：

(19)

故上述函数为凹函数且为次模函数。

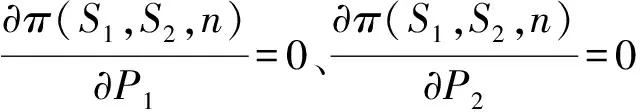
π(S1,0,n)=q1[r1+f-C1+V(S1-1,0,n-1)]+

q0V(S1,0,n-1)

(20)

则关于r1的一阶偏导数为：

[r1+f-C1-V(S1-1,0,n-1)-

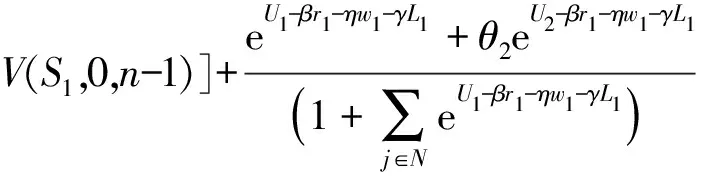
(21)

关于r1的二阶偏导数为：

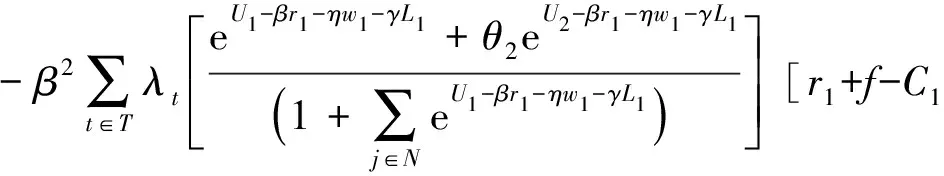
-V(S1-1,0,n-1)-V(S1,0,n-1)]+

(22)

2.3 客户满意度模型

所以，对于时隙i的客户满意度有：

(23)

式中：θ1表示价格指标权重；θ2表示交付期指标权重；θ3表示时隙宽度指标权重。

对三个指标进行分支估计，综合加权平均分值并构造比较数组，如表1所示。

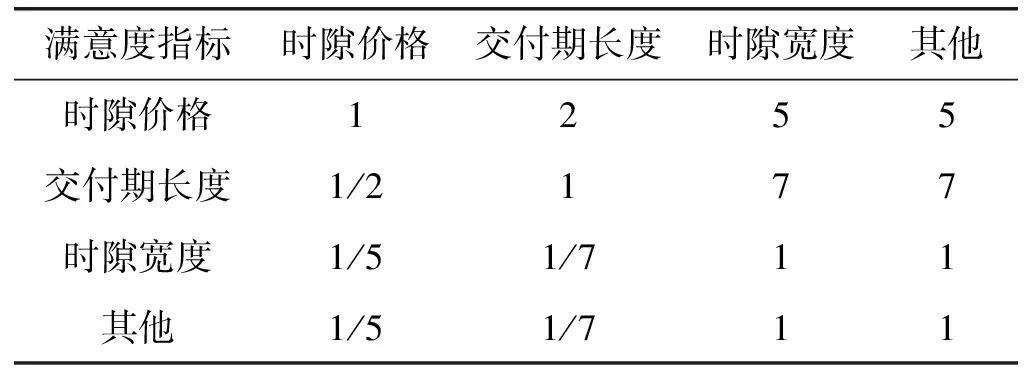
表1 比较数组

根据AHP层次分析法综合评定剔除“其他”同质要素，对于上述比较矩阵有最大特征根λmax=5.416 0,CI=0.104 0,CR=0.092 9，RI=1.12。

各个指标取值如表2所示。

表2 各指标满意度权重

所以θ1=0.507 7，θ2=0.411 6，θ3=0.080 7。

2.4 双重目标模型

本文将客户满意度引入到时隙定价过程中，在同时考虑期望收益和客户满意度双重目标之后，根据网络零售商对双目标的偏好程度，拟定契合网络零售商目标的时隙最优化定价方案。采取线性加权求和评价函数，建立包含客户满意度和期望收益的加权双目标优化模型，其中ζ为网络零售商对时隙即时收益的偏好程度；1-ζ为网络零售商对客户满意度的偏好程度。

maxY|Y=ζQ′+(1-ζ)Γ′

(24)

原式为：

(25)

式中：Y的值表示对网络零售商目标的贴合程度，越大则越符合网络零售商目标。Q′表示考虑时隙替代时的期望收益(单位)，其值等于1时表示当时隙2配送能力不足考虑替代时隙时期望收益取得最大值，Γ′表示考虑时隙替代时的客户满意度(单位)。

3 算例分析

为验证模型的有效性，选取小规模算例进行分析以降低模型求解的复杂性。假设2个时隙选项的预定时间范围均为120。本文运用求解工具MATLAB R2016b，求解环境为Intel(R) Core(TM)i5-3230M CPU @ 2.60 GHz RAM 8 GB。参数设置如表3所示。

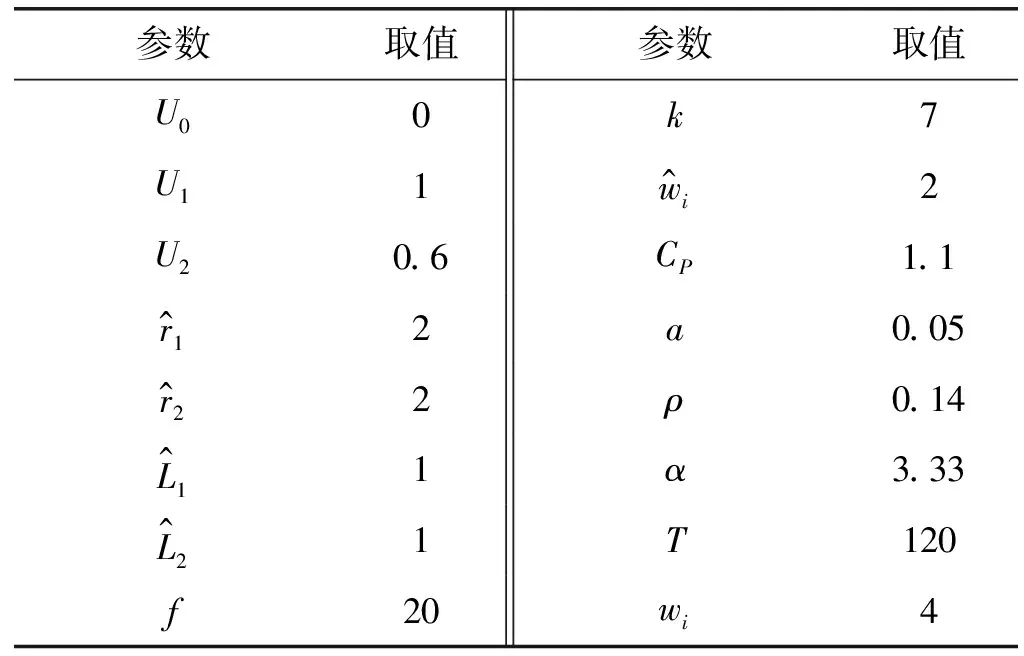
表3 相关参数设置

3.1 时隙价格、客户满意度与期望收益的关系

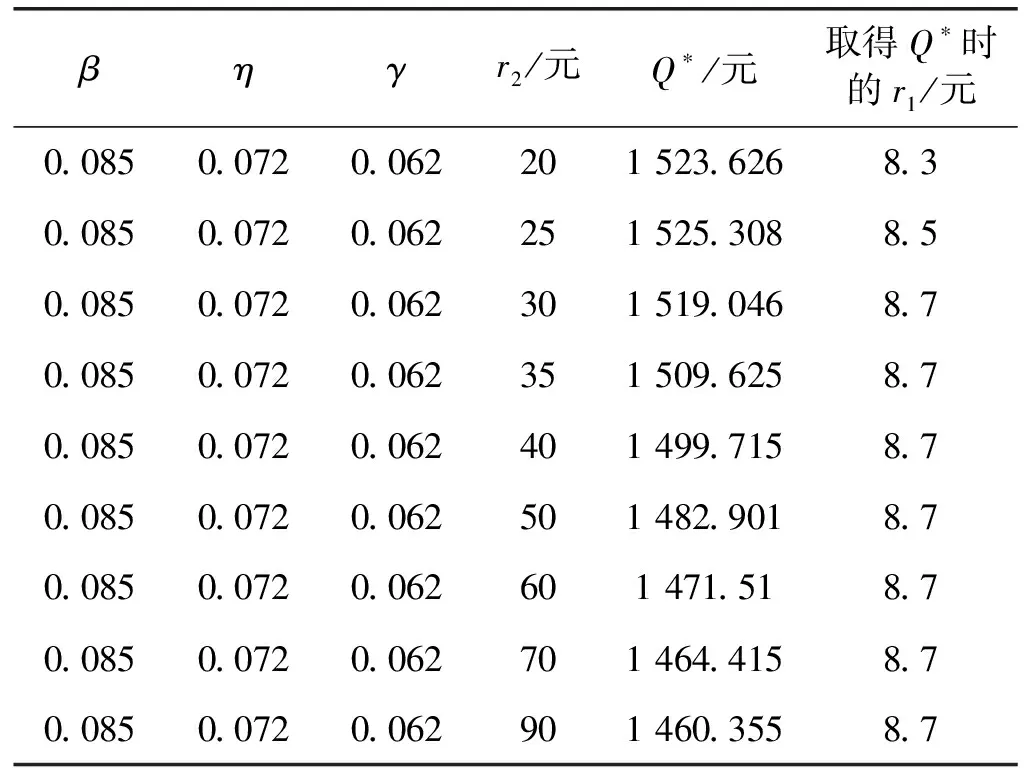
令客户选择模型中时隙价格、交付期和时隙宽度敏感系数分别为：β=0.07、γ=0.072、η=0.074。客户抵达率、时隙1和时隙2的交付期长度分别为固定值：λt=0.60、L1=2、L2=10，网络零售商收益偏好系数ζ=1。此时时隙1价格r1、时隙2价格r2与期望最佳收益Q*如表4、图1、图2所示。

表4 不同时隙2价格下的期望最佳收益Q*和时隙1价格r1

续表4

图1 不同时隙2价格r2下的期望最佳收益Q*

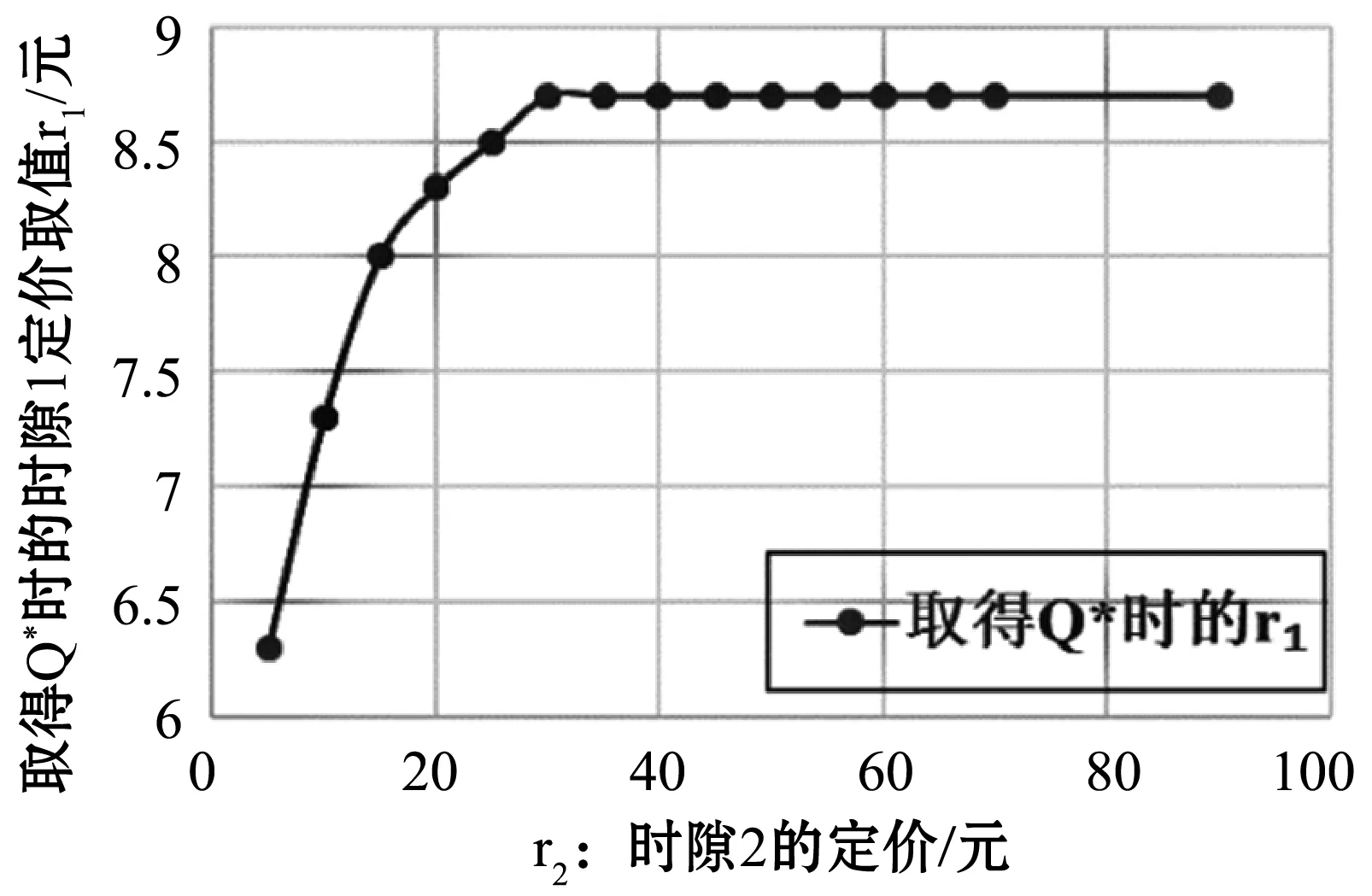
图2 不同时隙2价格r2下期望最佳收益Q*和r1

由表4和图1可得，由于时隙2价格的增加，期望最佳收益有先增加后减小的变化，如在r2=30时取得期望最佳收益的最大值maxQ*=1 525.308(元)，在r2=30之后，期望最佳收益逐渐减小，趋于稳定。

可以看出，在时隙替代过程中，考虑成本增加的情况网络零售商适当提高原时隙的售价，可以使得期望最佳收益达到最高，而过度地提高原时隙的售价会使得收益减少。

由表4和图2可得，在时隙2价格增大的过程中，时隙1的价格有先增大后稳定的变化，如当r2为50、70和90时，r1=8.7不变。当r2无限制增加时，由于选择r2的概率减小，导致期望最佳收益减小。

可看出随着原时隙价格的提高选择原时隙的概率减小，客户数量减少，而选择替代时隙的总客户数量也在减小，网络零售商不得不提高替代时隙的售价以维持收益，原时隙的售价达到定值时，选择原时隙的概率和客户数量达到最小，则此时网络零售商必需提高替代时隙的售价维持最佳收益。所以网络零售商在时隙定价过程中应适当选取原时隙的价格。

由表5和图3可知，当r2固定时，随着r1的增大，客户对时隙1的满意度减小，导致客户满意度Γ′逐渐减小，此时时隙替代过程中的期望收益Q′表现为先增大后减小的变化趋势，且在r1=8时，Γ=0.324时Q取得最大值(Q*=1 524.365)。

表5 不同时隙1价格下的Q*和Γ

图3 不同时隙1定价下的Q′和Γ′

可以看出，当网络零售商希望牺牲少部分客户满意度可以得到更高的期望收益，客户满意度大幅度减小时替代过程中的期望收益也会出现大幅度的减小。因此网络零售商应平衡客户满意度和期望收益之间的权重，不应以大量牺牲客户满意度为代价来换取期望收益的增加。

3.2 替代时隙交付期和时隙价格的关系

为研究在交付期不同长度下的时隙价格和期望最佳收益的关系，令β=0.07，γ=0.072，η=0.074，λt=0.60，L2=10，w1=4，w2=4，ζ=1。不同时隙1的交付期长度L1下的时隙价格和期望最佳收益如表6所示。

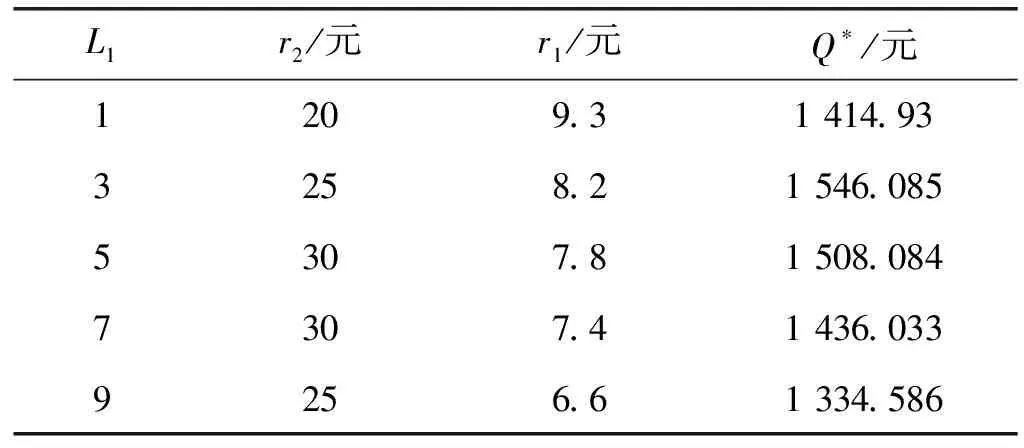
表6 不同L1下的时r1、r2和Q*

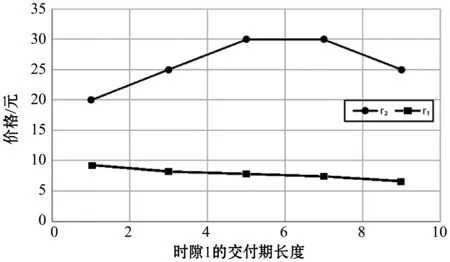
图4 不同L1下的r1、r2

可知，随着替代时隙交付期的增大，客户选择替代的概率减小，导致客户大量流失。此时降低替代时隙的价格可以提高收益，随着交付期的进一步增大，客户流失数量增大，导致降低替代时隙的价格不再能够提高收益。因此，网络零售商可以采取降低替代时隙价格增加原时隙价格的方式来维持高收益，同时，合理分配时隙交付期长度以降低客户流失率。

3.3 网络零售商不同收益偏好下的时隙价格

为研究不同收益偏好下的时隙价格，令β=0.07，γ=0.072，η=0.074，λt=0.60，L1=2，L2=10。在网络零售商收益偏好系数ζ分别为0、0.2、0.4、0.6、0.8和1时得到表7。

表7 ζ不同取值下的r1、r2和Q*

续表7

由表7和图5可得，由于ζ取值的不同，对应的时隙价格也不同，ζ取值增大，对应的时隙价格也得到增加，但是最佳收益Q*逐渐趋于稳定。所以时隙价格会根据网络零售商的收益偏好的差异化而定。随着网络零售商对期望收益偏好的增加，对客户满意度的忽视，此时客户选择率减小导致收益不再增长。

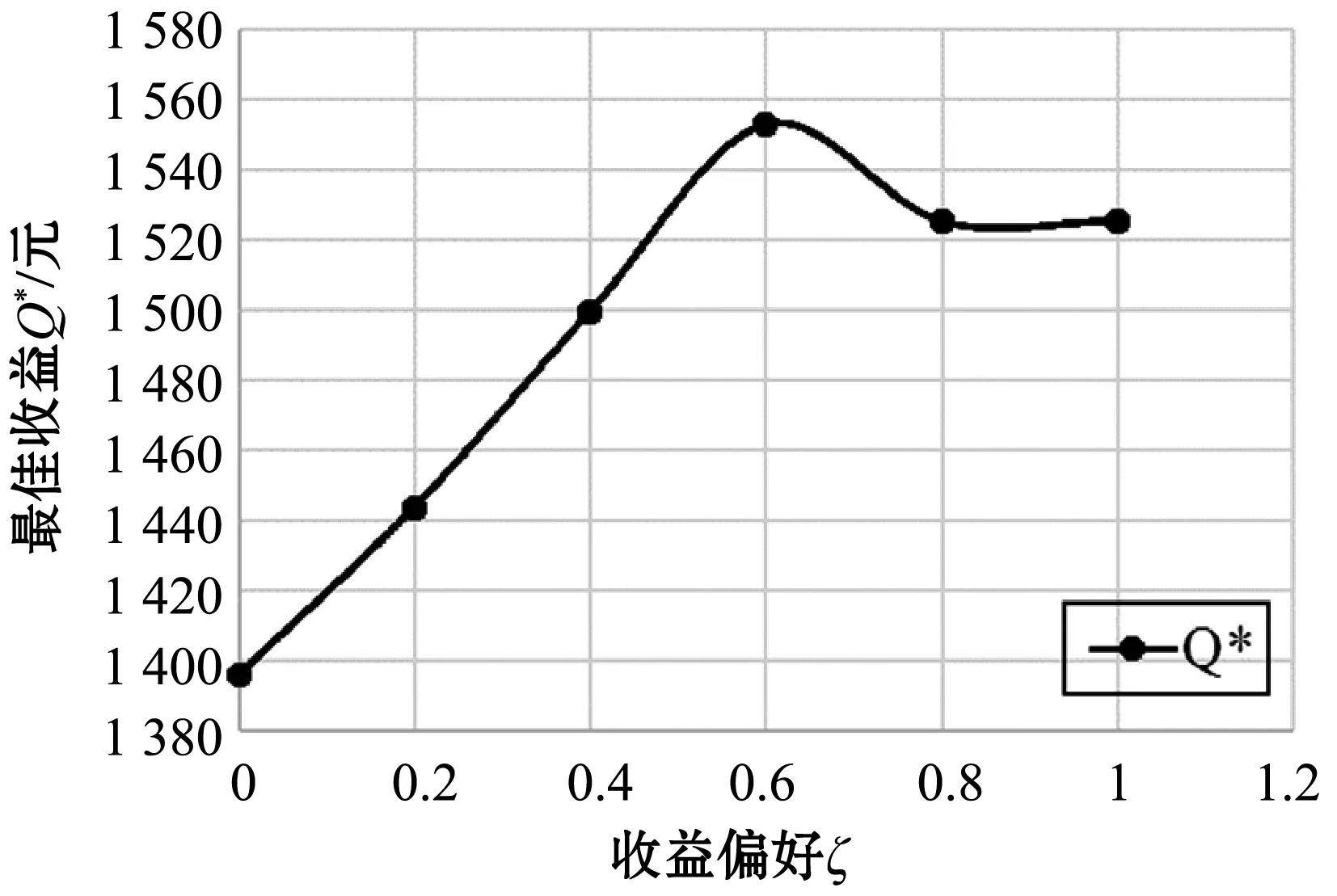
图5 ζ不同取值下的Q*

在时隙替代过程中，有下面两种情形：

(1) 考虑客户满意度时，ζ=0.6时候，收益有最大值1 552.815。此时r2和r1的定价分别为25元和6.7元。

(2) 若不考虑客户满意度，即ζ=1时候，双重目标定价模型则为以收益为目标的单目标模型，收益有最大值1 525.308，此时r1和r2的定价分别为25元和8.5元。

可知，在考虑客户满意度的时隙替代策略中，在满足客户价格需求的同时合理增大客户满意度的权重，可以获取更高的收益。对于不同发展时期的网络零售商使用阶段性的定价策略，对于发展前期的网络零售商可以偏重于客户满意度而选择少的收益，以维持客户数量，获得更长久的发展。对于发展成熟且更注重短期收益的网络零售商可以合理减小客户满意度的权重，来获得更高的收益。

4 对比分析

为证明上述结果的可信性，将根据表8中不同时隙价格得到的目标契合程度Y与根据取得最佳收益时的时隙价格得到的目标契合程度Y*进行对比。

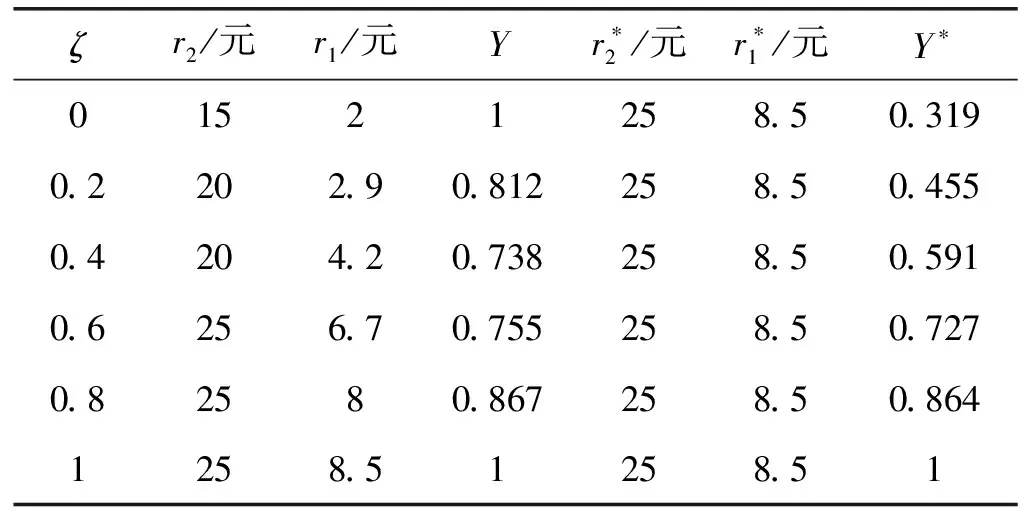
表8 目标契合度对比分析

由表8对比结果可知，前者更为符合网络零售商目标需求。

5 结 语

本文研究了在线时隙替代过程在客户满意度和网络零售商期望收益双目标下的时隙定价策略。在讨论了不同因素影响下的期望收益、客户满意度与时隙价格之间的关系之后，得出以下结论：

在网络零售商仅考虑期望收益的情况下，双重目标模型转变为单目标模型，网络零售商趋向于采取提高替代时隙的售价的方式以维持高收益；在网络零售商考虑期望收益和客户满意度双重目标的情况下，对于不同的收益偏好ζ都存在一组最优时隙价格，使得网络零售商目标契合度Y最大；随着收益偏好从0到1的增大，网络零售商越重视期望收益，则倾向于制定较高的价格以获取更高的收益，同时客户的满意度降低。对于不同发展阶段的网络零售商可以根据自身目标需求制定相应的时隙售价：对于发展前期的网络零售商，对客户的满意度较为重视，可采取稍低的时隙价格；对于发展后期的网络零售商有条件选择采取稍高的时隙价格，以获得更高的收益。在时隙选择替代过程中，替代时隙的价格随其交付期的增大而减小，当交付期较小时，网络零售商可以制定稍高的时隙定价。在模型实际运用过程中，网络零售商可以根据实际情况对其中的参数值进行重新制定以得出更为合理的定价策略。

在以后的研究中，计划考虑存在多时隙替代时的时隙定价情况，进而将客户具体分类，寻求满足不同客户需求的最佳时隙定价，使零售商获得更高的收益。