电厂废水中和过程的CPSO-RBF神经网络预测控制
2018-10-24任志玲孙雪飞
任志玲 孙雪飞
(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105)
0 引 言
在现代300 MW以上火电厂中,水处理自动化系统的投入率以及使用效率很低。主要是因为该控制过程具有强时滞性、强非线性和强时变性,系统增益变化尺度大,传统的PID控制器参数难以确定合理值,增益变化无法满足要求,控制响应速度慢、精度低,全局控制品质差,浪费中和剂剂量,设备损坏耗大。因此迫切需要一种响应速度快、鲁棒性好、精确性高的控制算法来提高电厂废水中和的全局品质把握,实现用水的高效化、节能化、节约化。由于神经网络能够任意精度逼近非线性函数以及优良的数据预测评估能力,目前已被大量学者运用在废水中和过程的辨识和控制中,文献[1]设计了一种神经网络与传统PID相结合的控制方式,一定程度上改善了PID控制的鲁棒性。文献[2]则设计了一种将遗传算法(GA)结合BP神经网络实现优化的控制方法。文献[3]构建了递归模糊神经网络(RFNN)模型,同时利用广义预测控制器(GPC)控制pH中和过程,精度理想。但是上面所列几种算法计算量庞大、收敛速度也不理想。为此,设计以优化径向基函数神经网络(RBFNN)为模型的预测控制。该算法在优化RBF网络结构时保持了种群多样性,也提高了传统粒子群算法收敛速度,再以优化后的神经网络辨识出系统迟滞时间从而实现提高系统整体的响应速度和精度。
1 中和过程的强酸当量模型
由于电厂废水反应池中和溶液中存在一些不能完全电离的弱酸弱碱[5],检测仪测定pH值与实际值之间有很大的偏差,仅根据测得的pH值难以获得将溶液中和到中性时所需的中和剂的准确值,常规的由化学方程及质量守恒公式推导的中和反应模型已不能满足精度要求和现实需求。而强酸当量能综合反映废水的酸碱水平,它能比较直观准确计算需要的中和剂量,同时为了减少扰动影响,引入水流速S,将其由扰动量变为输入可控量,提高了系统的响应速度和鲁棒性。强酸当量Y可表示为:
(1)
式中:强碱时ai(pH)=+1,强酸时ai(pH)=-1;bi为氢离子的浓度;pH是强酸当量的函数,可表示为:
(2)
式中:KW表示水的离解常数。假设情况:弱酸、强碱中和反应,同时假设反应充分且各个时刻温度条件保持恒定,得到基于强酸当量设计的pH中和过程模型为:
(3)
式中:V为反应池体积;PKa=-log10Ka,Ka表示酸的离解常数;u为加入强碱的流量;α表示强碱的浓度;F表示强酸当量系数。
2 废水中和过程神经网络辨识
2.1 RBF神经网络模型结构
RBF神经网络基本思想是将低维空间非线性关系通过相应的基函数投影成高纬空间的线性关系。训练方法快速易行,自学习和容错性能理想,是三层前向网络,输入层由信号源节点构成,隐层的单元数由问题需要决定,输出层输出是隐单元输出通过线性加权得到[6]。图1为RBF神经网络分解结构图。
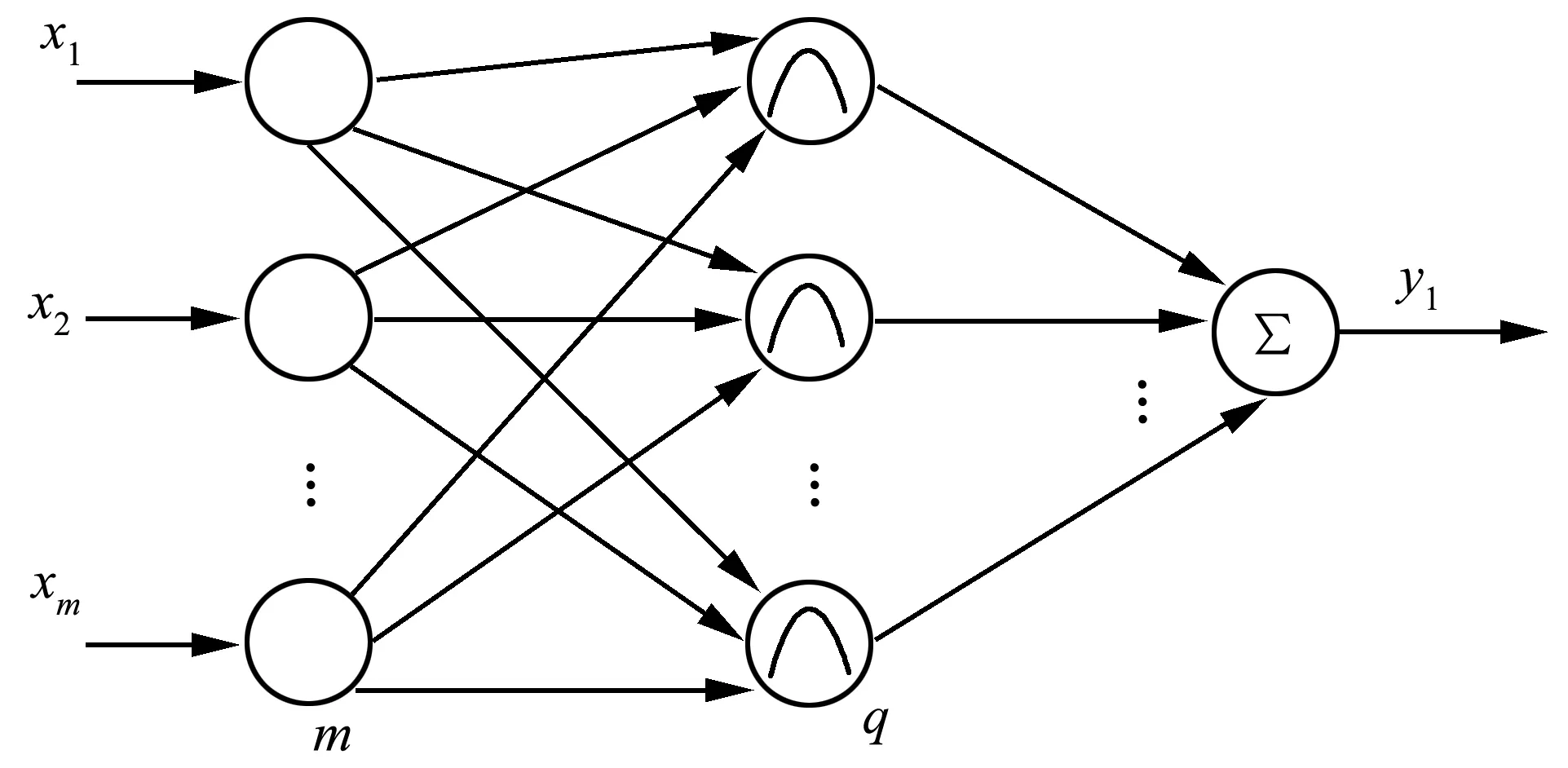
图1 RBF神经网络结构分解图
图中有m个输入,q个隐层,1个输出,设输入和输出分别为:
x(k)=[x1(k),x2(k),…,xm(k)]
(4)
(5)
式中:δi为函数的径向基宽度参数;‖·‖为Euclidean范数;ci为隐层第i个神经元中心。
2.2 混沌粒子群法(CPSO)
以混沌算法遍历性等特点弥补传统粒子群算法的早熟、搜索速度慢的缺点。粒子的位置和速度迭代公式如下:
(6)
(7)
(8)
式中:k为迭代次数;wi和wf分别表示最初和最终的权值。CPSO算法中将常规随机序列换成混沌序列,从而具备了遍历性和伪随机性的优势,可以实现全局优化。用改进的Logistic映射产生混沌运动,其方程为:
x(n+1)=1-r(x(n))2
(9)
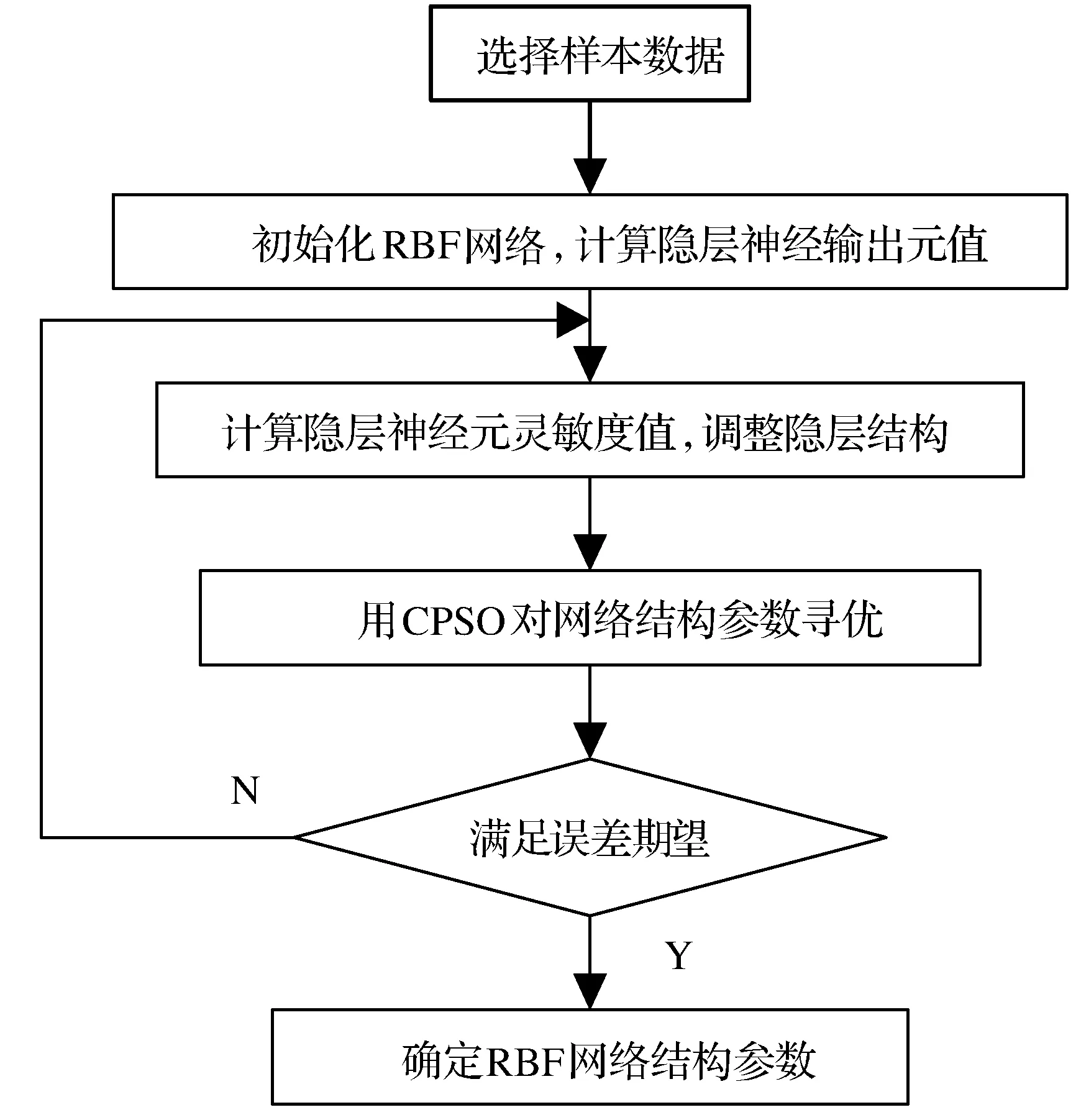
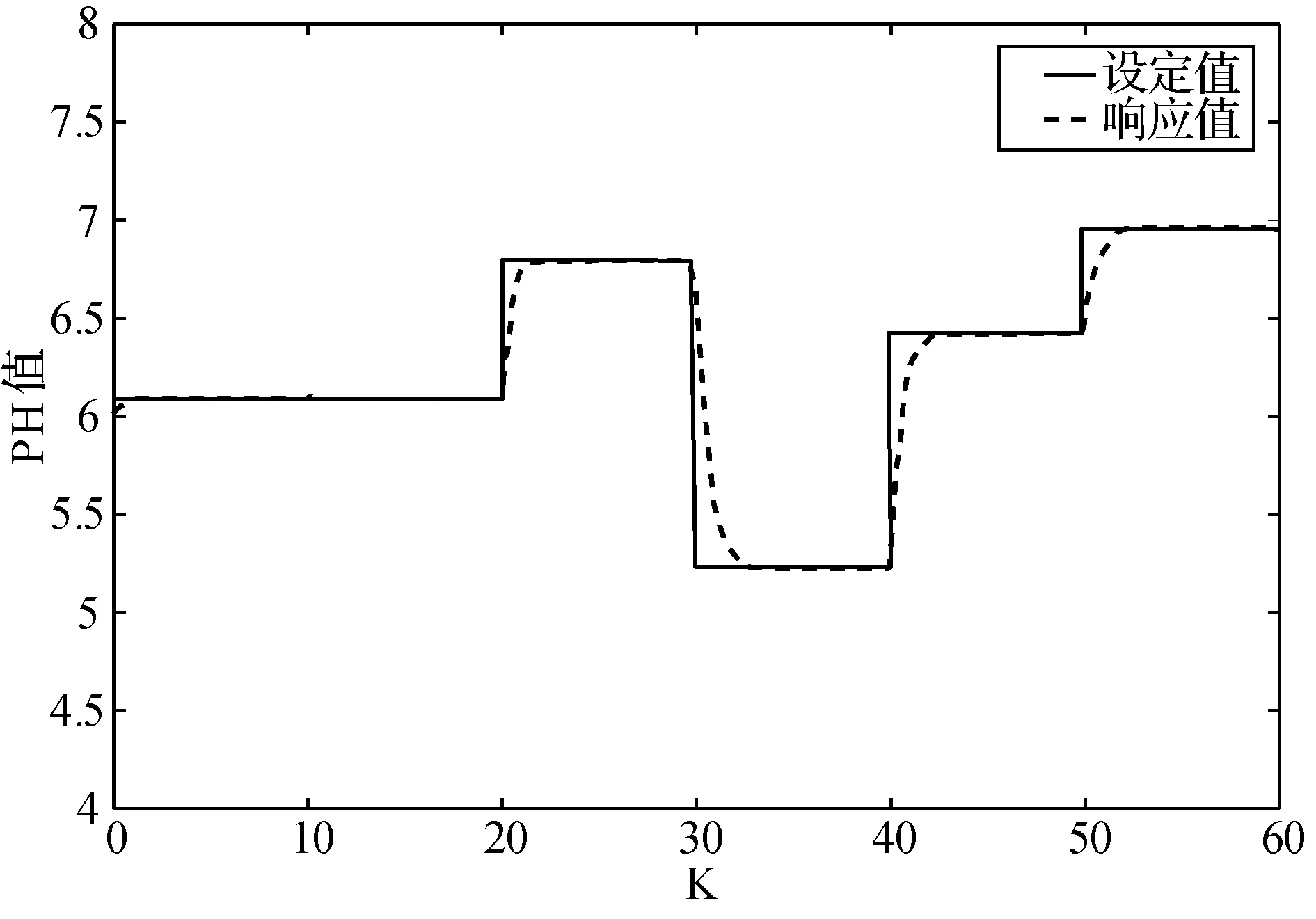
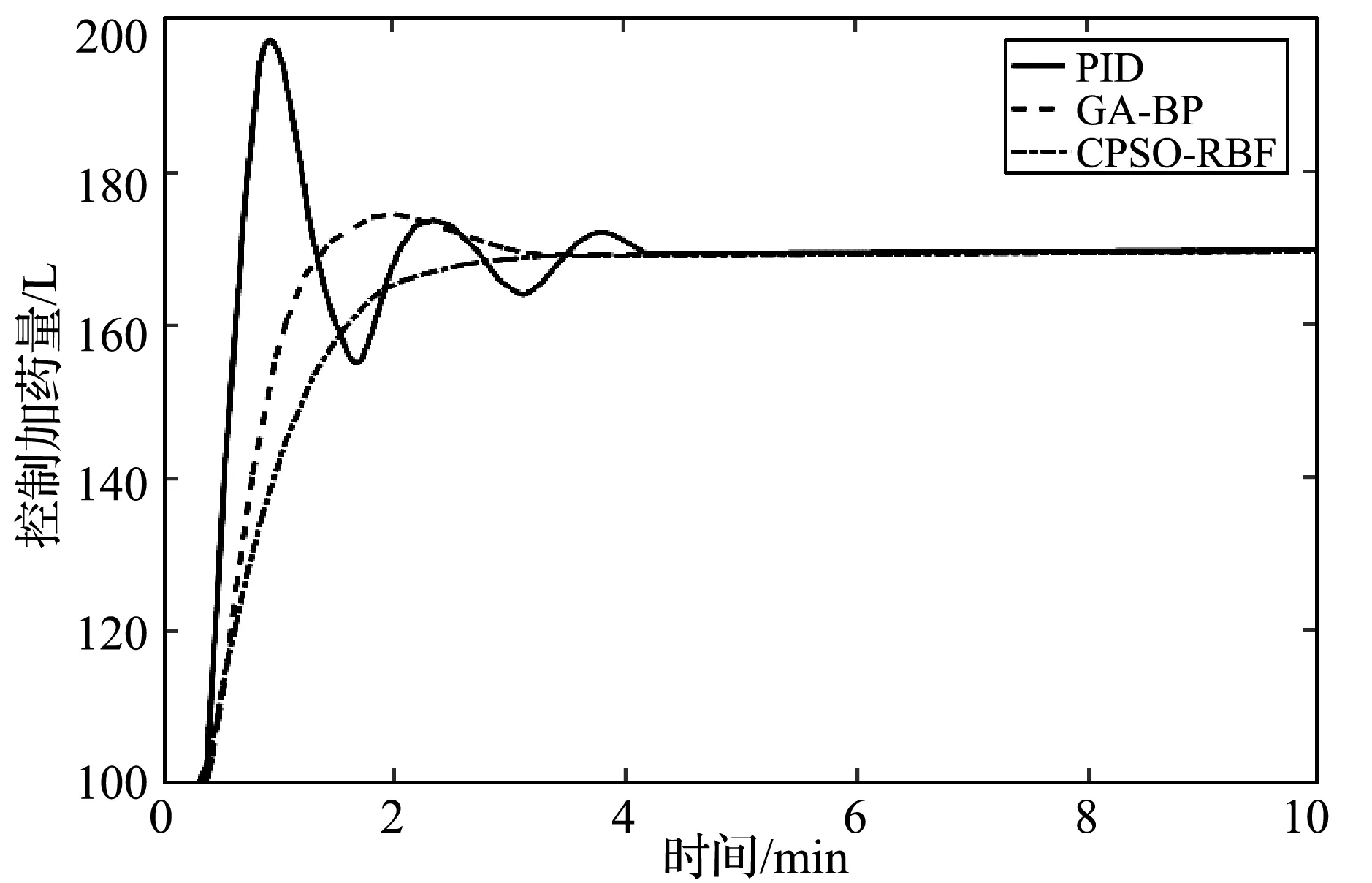
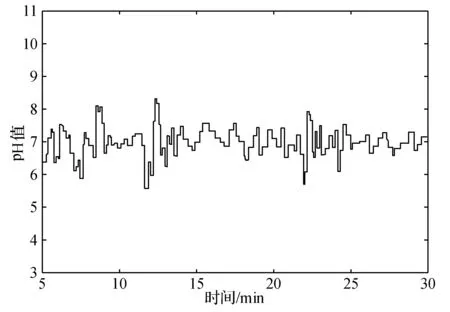
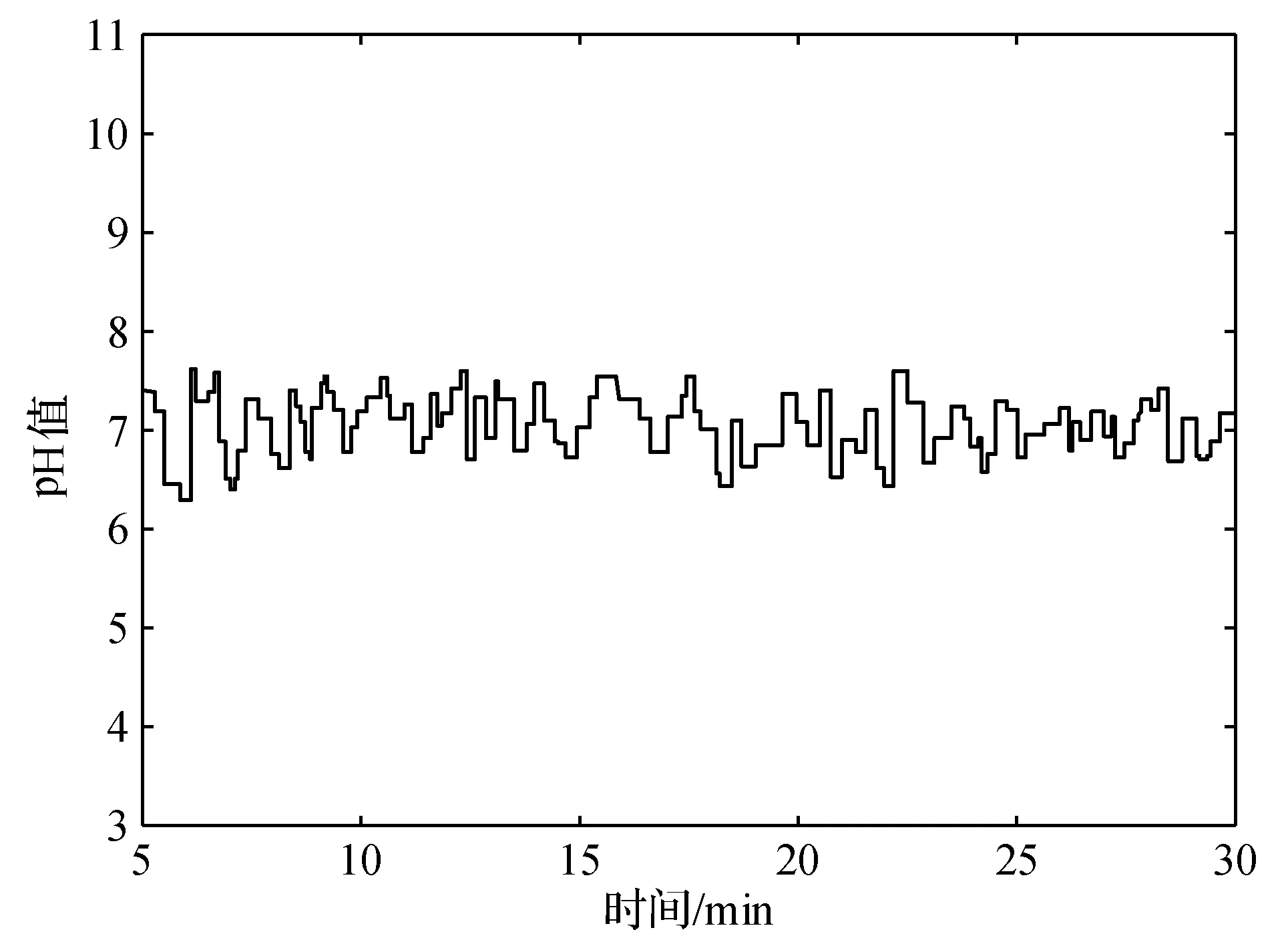
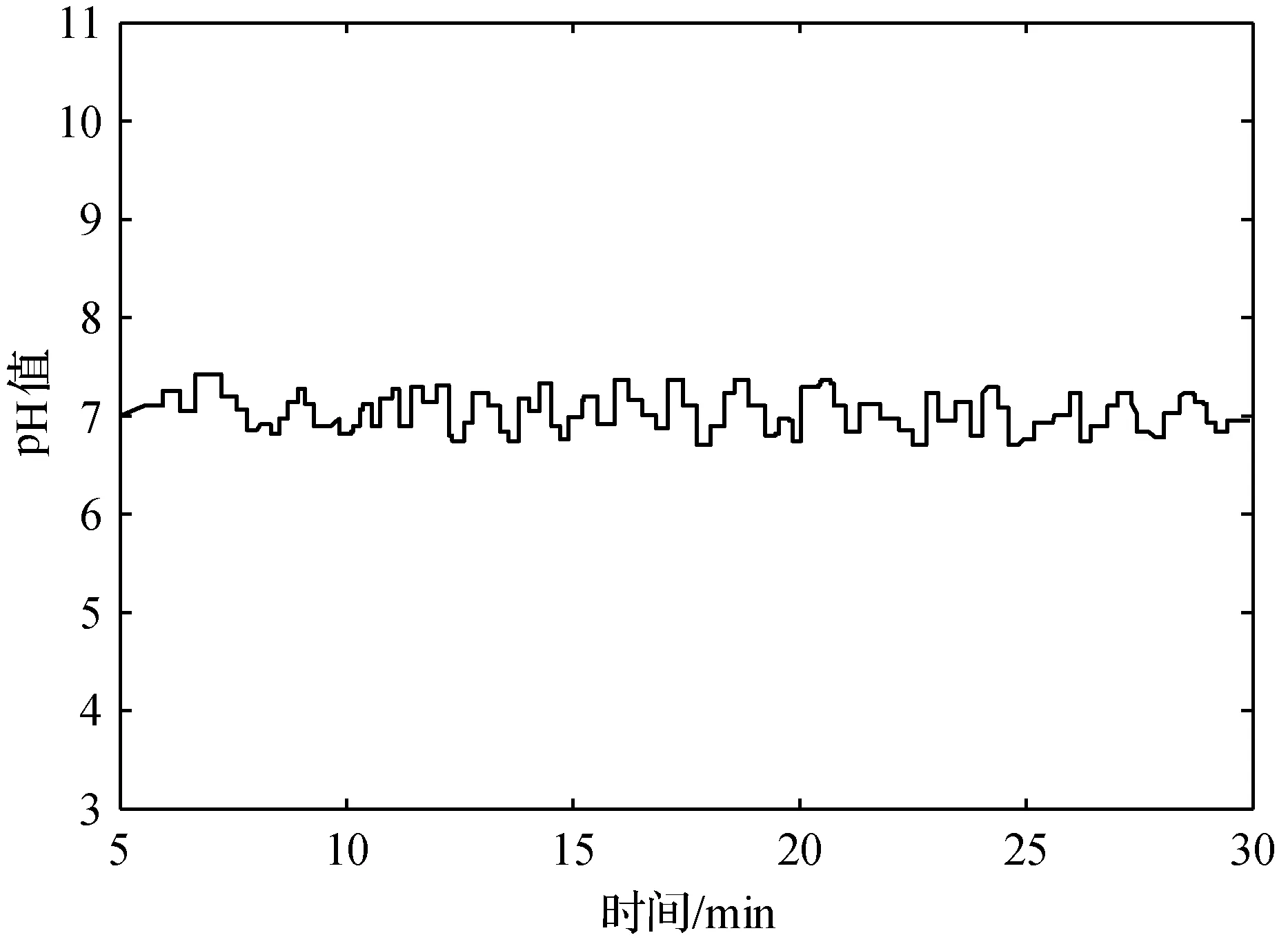
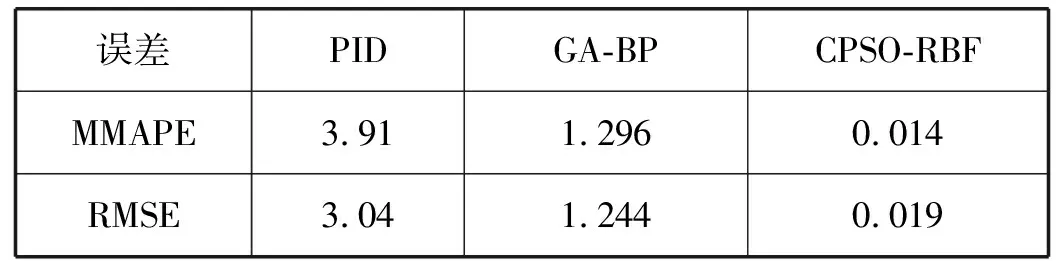
式中:0 ① 确定最大混沌搜索步数cmax=25;优化区间设为(xmini,xmaxi),同时不定向初始化m个混沌变量xi∈(-1,1),i=1,2,…,m;Xbest=Xg,fbest=fg; ② 根据迭代公式进行迭代,持续得到未来变量值; ③ 将迭代所得混沌变量映射到区间(xmini,xmaxi),接着用公式来确定优化量: (10) ④ 计算适应度值fn+1,若fn+1 ⑤ 当到达预设迭代最高次数时则退出迭代、退出算法,否则转到步骤②继续循环迭代优化过程。 (1) 编号。先假设RBF结构如图1所示, 将其网络参数看作为一个粒子,粒子编码为: S=(X1,X2,…,Xq) (2) 子群划分。先将所有粒子分成S份不同量级的粒子, 而每种量级粒子有不同的维数。将每个粒子相对应的量级粒子组合成一个子群体[10], 最后划分出S个子群体。 (3) 适应度计算。取目标函数为均方误差: (11) (4) 算法终止条件。当计算所得适应度值小于预设代数值时,算法终止并输出参数,另外如果算法到达预先设定的最大迭代次数时也会停止。 灵敏度法(SA)是分析一个系统输出值相对于预先设定值发生各种变化时,系统参数在这种变化的影响下而改变的敏感程度[11]的方法,根据不同数据灵敏度的大小不同,删除无效数据,以此来缩小优化区间。 在初步训练后得到一个RBF神经网络,然后计算出不同隐层对网络最终输出的影响度并删改隐层: (12) 式中:Es(h)是whφh(x)对输出值y的灵敏度;zh是隐层输出与相应权值的积;Vh[E(y|zh=whφh(x))]的大小表示zh对y方差的影响。 引入灵敏度法(SA)进一步提高CPSO算法优化效率,提高模型辨识精度,灵敏度算法利用控制对象的输入输出量来修正网络结构信息参数。在进行网络结构参数辨识时,将滞后时间τ与权值间的关系用ω(τ)表示,并且加以训练,τ∈[t1,t2],t1、t2为设定的迟滞时间范围,可借此预设范围进行搜寻准确值。 SA-CPSO算法优化,第一步可称为离线训练,采用所获得的历史运行样本数据进行网络训练学习(步骤见图2)。然后在此基础上进行第二步优化,即进行在线辨识,导入系统实时输入输出数据及误差,实现对神经网络参数同步校正。离线结合了在线优化,既提高了预测精度又有效减少参数寻优时间。 图2 CPSO算法流程 预测控制系统结构如图3所示。 图3 预测控制系统结构图 图3中系统有预设值输入环节、控制器、系统模型、预测模型和反馈校正几个部分。预设值输入环节仿真时可直接设定;神经网络控制器(NNC)由辨识优化后的RBF神经网络构成,其输入包括已知的预设值和反馈环节的反馈量;控制器的输出作为系统模型的控制量对加药泵加药量的快慢进行控制;系统模型则是已选择的强酸当量模型;预测模型的输入包括控制器输出的控制量和当前系统模型输出值,输出当前和下一时刻两个值。 系统模型式(3)离散化后得到: y(k)=f[u(k-d),…,u(k-m-d),y(k-1),…,y(k-n)] (13) 该模型左边为输出值,右侧为输入值的函数,其中:d为非线性系统的滞后拍数;m、n为系统阶次;y(k)为期望输出;f(·)为RBF神经网络实现的非线性函数。式(9)可用如下模型来预测y(k+1)时刻的值[12]: m),y(k),…,y(k-n+1)] (14) m),y(k+p-1),…,y(k-n+p)] (15) 预测控制中,反馈环节至关重要,即使系统控制器和预测模型经过优化,输出值与实际值仍然存在不可忽视的误差,借助反馈校正环节,实时调整控制参数,减小系统误差则尤为重要,时刻补偿误差,时刻保持系统模型最优。采用误差补偿系数hi∈[0,1],其值越接近1,反馈校正越强,其值越接近0,反馈校正能力越弱。补偿后的预测输出为: (16) 本文控制系统中预测控制器(NPC)是由优化后的RBF神经网络构成,相比优化前,控制器的跟踪能力和稳定性进一步提高。RBF预测控制器的输入为 H(K)=[u(k-1),…,u(k-m),ycor(k+ p-d),…,ycor(k-d),yr(k)] (17) 输出为: U(k)=[u(k),u(k+1),…,u(k+M-1)] (18) (19) 采用式(3)表示的系统模型,取加权因子ai=-0.5,-0.7,碱液浓度取30 %。设定时域长度P=3,然后使用SA-CPSO算法对RBF结构进行优化。设CPSO参数:粒子数m取20个,惯性权值ω∈[0.9,0.3],学习因子c1=c2=2.05,经过200次训练学习得误差SSE=1.288。神经网络控制器的初始结构设定为3-5-2,并且设定控制时域M= 2,误差补偿系数设定hi=[0.8,0.6,0.4];仿真如图4所示。 图4 预测控制仿真图 由图可看出本文所设计预测控制算法具有较好的跟踪性、鲁棒性,而且超调小,能够及时灵活地跟随设定值改变控制器参数。 以某电厂2×300 MW机组废水处理系统数据作为本文仿真数据来源,该厂目前在用的控制方式为PID控制,训练预测控制器时选用部分历史数据,样本采集周期T取60 s。在剔除一些不可靠数据后,抽取100组具有代表性的样本,用于预测模型和控制器的训练,可得τ为115 s,d为2,τ表示纯滞后时间,d表示拍数。不同控制策略的实时控制加药泵加药量和输出稳定后pH值的响应曲线对比如图5和图6所示。 图5 控制加药量响应曲线 图6 pH值PID控制效果图 由图5可以对比分析,PID控制方式对加药量和pH值的控制超调量大,调节时间长,控制效果最差。GA-BP控制策略的曲线波动比PID控制方式的略微平稳,超调量稍小,但任然存在,另外该算法达到稳定值所需时间也有所减小。而本文所提CPSO-RBF控制方式具有最短的调节时间和微小的超调量,节约药剂量优势明显。比较分析图6、图7、图8不同控制策略的pH值效果图,可知本文所提控制方法能够实现pH值稳定在最小的波动区间,精确性和鲁棒性最佳。综上说明该控制方式成本最低,控制效果更好。其主要原因是RBF模型训练效果好,精度高,水流速及进口pH值的扰动被考虑在了系统模型中,对系统输入和扰动实现了整体控制。 图7 pH值GA-BP控制效果图 图8 pH值CPSO-RBF控制效果图 计算绝对平均误差(MMAPE)和均方根误差(RMSE)。 (20) (21) (22) 式中:y(k)为第k个输出的pH实测量;yr(k)为第k个pH设定量;M=100为选取点的个数。由式及控制输出pH值即可得如表1所示三种控制策略的误差值。 表1 误差值 分析表1可知,本文所提预测控制输出误差明显小于常规PID控制和GA-BP控制,输出pH 控制在6.6~7.4之间,输出值的变化最为平稳。以在同样设备和环境条件下处理100 t相同成分含量废水为例,加药量量化后由传统PID控制的0.3 t减少为预测控制的0.22 t,废水用药量和加药泵能耗明显减少。 本文所提控制策略,计算量小、响应速度快、鲁棒性好,在辨识优化中引入灵敏度法(SA)有效缩短优化区间,提高辨识速度,预测模型采用辨识优化的神经网络设计。由仿真实验结果分析可知,本文设计的控制方式能够满足中和系统增益变化尺度大的特性,能够满足系统对全局控制品质的要求,为电厂废水处理的智能控制提供理论依据。2.3 基于CPSO算法的RBF神经网络
2.4 SA-CPSO模型辨识算法
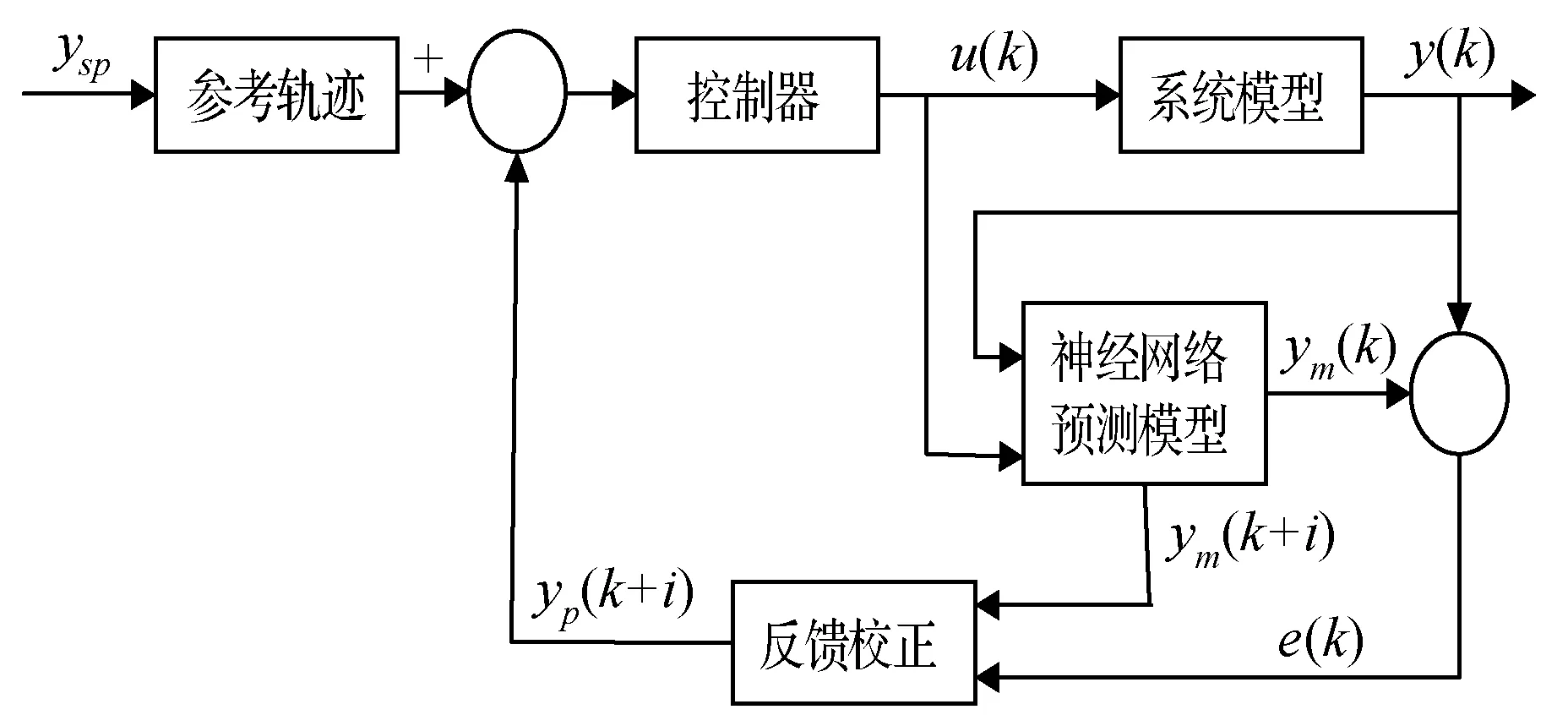
3 废水中和过程的预测控制
3.1 预测控制系统结构
3.2 神经网络模型的多步预测
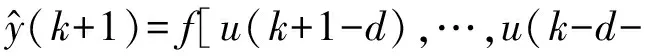
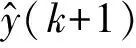
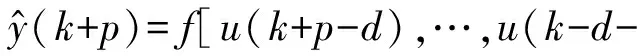
3.3 反馈校正
3.4 RBF神经网络控制器(NPC)
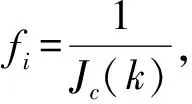
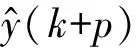
4 系统仿真与试验分析
4.1 pH值预测控制系统仿真
4.2 仿真实验对比
5 结 语
