以ARIMA模型为依托对江苏省居民消费水平进行分析建模与预测

卢颖伟 南京财经大学应用数学学院

一、ARIMA理论与方法分析

ARIMA即时间序列分析的英文简称，为常见的数量分析方式，用于对事物随时间变化呈现出的数量变化规律进行阐述和描绘。采用该方法，需要建立相应的时间序列。伴随着时间的推移，针对预测对象将完成全新序列的组建。而序列数据随机性较强，需要借助数学模型对序列真实内涵进行全面分析。因此借助数学模型，也可以对时间序列未来趋势进行预测[1]。在现实生活中，形成的时间序列多为非平稳序列，变化受各种因素影响。其中一些因素将起到决定性和长期的作用，促使时间序列呈现出一定变化规律和发展趋势。而部分因素将发挥非决定性和短期作用，导致时间序列不规则变化。将这些因素去除，则能对序列变化趋势进行分析。如式（1）所示，为ARIMA（p,d,q）模型结构。式中，Φ（B）=1-φ1B-……-φpB指的是平稳可逆（p,q）阶自回归移动平均模型自回归系数多项式，Θ（B）=1-θ1B-……-θqB则为移动平滑系数多项式。从本质上来讲，ARIMA模型为差分运算和自回归移动平均模型的组合。

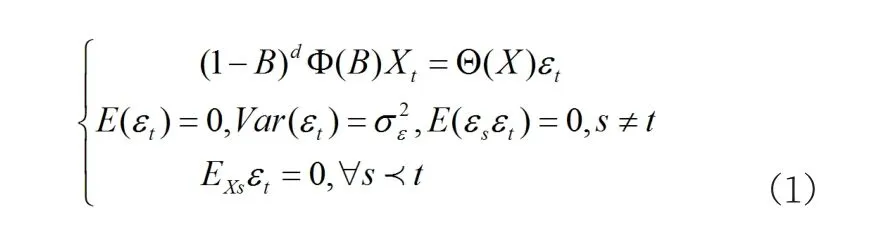
二、江苏省居民消费水平的分析建模与预测

在经济增速放缓的背景下，各地经济发展都受到了一定影响，以至于居民消费水平也随之受到了影响。相较于其他省，江苏省经济发展位列全国前茅，在经济结构转型过程中还应加强调控。因此，还应建立模型对江苏省居民消费水平进行分析和预测，确定江苏省居民未来消费水平变化情况，从而采取有效促使减少经济结构转型给居民生活带来的影响。

（一）数据分析

实际采用ARIMA模型对江苏省居民消费水平进行分析和预测时，需要利用Eviews软件进行模型的建立。从2013年到2017年江苏省居民人均消费水平走势来看，呈现出逐年提升的发展趋势。根据国家统计局的数据可知，2013年，江苏省居民人均消费17925.75元，2014年、2015年、2016年和2017年则分别提升至19163.56元、20555.56元、22130.37元和23468.63元。得到的时间序列呈现出确定性的上升趋势，类似指数增长。由此可知，在较长时间内，受某些确定性因素的影响，江苏省居民消费水平呈现出持续上升的趋势。为对这些趋势进行拟合，还要利用软件建立相应的数学模型。

（二）参数估计

假设江苏省居民消费水平序列为X，对其进行带趋势项和常数项ADF检验，可以得到检验统计量P为1.由此可见，X显著接受存在一个单位根的原假设，由此可知时间序列并不平稳。在江苏省居民消费水平不断提高的背景下，可以得到近似指数函数的曲线，需要利用对数函数进行明显上升趋势的消除。利用获得的新序列Y完成ADF检验，可以得到检验P值为0.9045。未能通过检验，证明序列依然不稳定，因此需要进一步进行差分处理，得到新序列。经过一阶差分处理后，可以将序列趋势基本全部清理，得到符合各种要求的平稳时间序列。重复进行检验，则能得到P为0.0428，最终得到了平稳序列YT。针对序列，利用软件得到相关系数图，则能完成ARMA模型的建立。从分析结果来看，居民消费指数自相关系数不断降低，通过差分处理后则接近0。由此可知，原本得到时间序列无法满足平稳要求，但是经过差分处理得到的序列趋近平稳。采用最小二乘数法对模型参数进行估算，则能得到两个适合的模型。如表1所示，为两个模型检验参数。通过对比，可以发现模型ARMA（1,5）拥有更大的R-squared，因此可以证明模型因变量能够更好的对自变量进行解释。根据统计学理论得知，数据间拥有显著差异性才具有统计学意义，从而判断出得到的模型序列为白噪声序列，具有较强的实效性和差异性，能够利用得到的模型对居民消费水平变化趋势进行预测分析。而该模型拥有较小的SC和AIC，所以容易拟合，可以完成ARIMA（1,5）模型的建立。

表1 模型检验数

结论：采用ARIMA模型对江苏省居民消费水平进行分析和预测，还要完成相应时间序列建立，然后结合时间序列变化趋势进行处理，得到平稳的时间序列，从而完成分析模型的科学构建。在此基础上，才能得到具有较好拟合效果的分析模型，实现对居民消费水平变化趋势的合理预测。从预测分析结果来看，江苏省居民消费水平在未来将得到进一步提升，政府还应采取措施预防通货膨胀效应的发生。