基于MAX274的多通道有源低通抗混迭滤波器的设计

卢育中 李春风

（91388部队95分队 湛江 524022）

1 引言

在水下目标测量试验中，由于受海浪、海流冲击等外部因素，造成获取目标数据存在较大外部干扰信号，给目标数据分析处理带来了较大的影响，如何去除外部干扰噪声，提高信号录取的质量，准确获取目标特征是测量系统设计的一个难题［1］。本文介绍了一种基于MAX274芯片［2］设计制作多通道抗混迭滤波器的设计方法并应用于实际水声信号的采集记录电路，得到了很好的实际应用效果，有效信号录取的质量。

2 滤波器的选择

根据噪声测量系统对水声信号处理的实际测量要求，为了消除海洋中高频的干扰噪声，无失真还原信号，在A/D转换采集记录之前对水听器信号进行抗混迭低通滤波处理，滤除高频信号干扰，在低频范围内，在接近通带的止带产生最佳的衰减，对滤波器特性诸如带内平坦度、带外衰减、过渡带宽度等参数有较高要求时，因此往往采用高阶有源滤波器。通常的有源滤波器是由运算放大器及R、C电路组合而成［5］。由于阶数高，因而使用的元器件也比较多，这样设计出的RC有源滤波器进行参数调整特性亦会造成很大影响，最终的效果并不是很好。加之在设计RC滤波器时，我们还不得不考虑谐振现象。因此，一般说来，具有较大R值的RC滤波器是比较理想的，它不会产生明显的谐振。但在信号频率为几kHz以上，或传输率为kb/s以上的电路中，高R值是不合适的。

Chebyshev滤波器［11］的设计就是为了在接近止带产生最佳的衰减，即，具有最快的滚降。但是它在相位上不是线性的。也就是说，不同的频率分量要至少受同时间延迟的支配。

Bessel型滤波器同受到广泛应用的Buterworth滤波器相比，具有最佳的线性响应，但是滚降就慢得多，并且较早就开始滚降。逐次增大阶次的Bessel滤波器能获得改善的线性相位函数。

椭圆函数滤波器可以产生比Butterworth、Chebyshev或Bessel滤波器更陡峭的截止，不过却在通带和止带代入内容复杂的纹波，并造成高度的非线性相位响应［4］。

通过对比以上三种类型滤波器的特点以及在接近通带的止带产生最佳的衰减等系统设计要求，我们选择了Chebyshev类型滤波器。

3 Chebyshev高阶有源低通滤波器设计原理

3.1 MAX274芯片特点

MAXIM公司开发的8阶连续时间有源滤波器芯片MAX274将4个二阶节合而为一，最高中心设计频率可达150kHz。该滤波器不需要外置电容，每个单元二阶工的中心频率F0、Q值，放大倍数均可由其外接电阻R1～R4的设计来确定。集成化后的二阶节较之由运放和R、C电路组成的二阶节，其外接元件少、参数调节方便、不受运放频响影响，对电路杂散电容也有更优的抗干扰性。

MAX274是包含四个互相独立的二阶滤波单元的高效和集成芯片。通过调整外接的几个电阻，可以组成各种高阶有源低通、高通、带通滤波器，如Butterworth、Chebyshev、Bessel和椭圆函数型等。

采用MAX274/275芯片设计高阶的低通滤波器，对于相同设计指标，Chebyshev和椭圆函数型滤波器，所需二阶节数少于Butterworth、Bessel型，并且MAX274不支持椭圆函数型带通滤波器结构。

图1 二阶滤波单元的原理图

3.2 设计原理

根据MAXIM提供的滤波单元原理图，我们可以先求出所需滤波器的频谱（幅度谱）表达式，计算出滤波单元的传输函数，然后再通过调整滤波器的品质因数Q、增益G和带通滤波器的中心频率F0，用实际滤波器的频谱来似合所需的频谱，图1是二阶滤波单元的原理图。

图1中，整个滤波单元外接四个电阻R1、R2、R3、R4，其余元件封装在芯片内，并有准确参数。每个滤波单元有五个外接管脚，分别为输入（IN）、带通输入（BPI）、带通输出（BPO）、带通输入（LPI）和低通输出（LPO）。图中

系统的截止频率为：

低通滤波器直流输出增益HOLP为

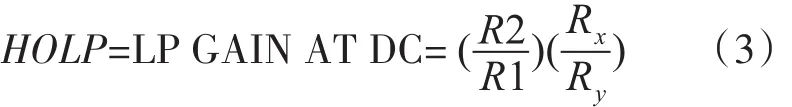
滤波低通信号输出如图2所示。

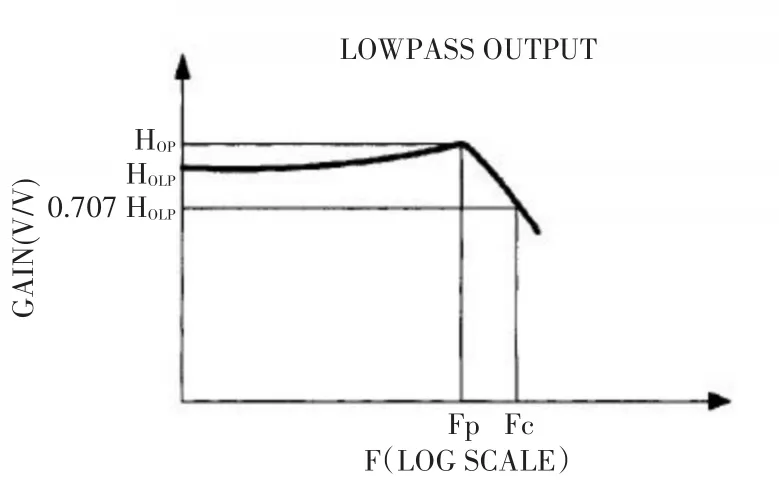
图2 滤波低通信号输出

图中，系统传递函数G（s）为

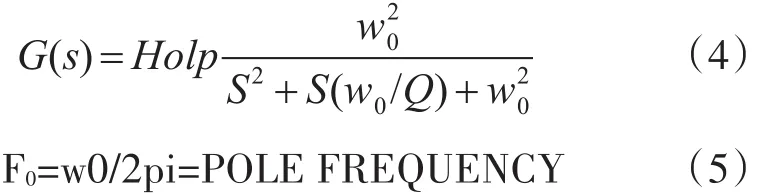
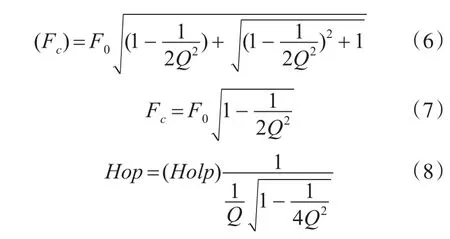
根据以上关系式（1）可知，R2和R4的阻值决定截止频率F0，且有，

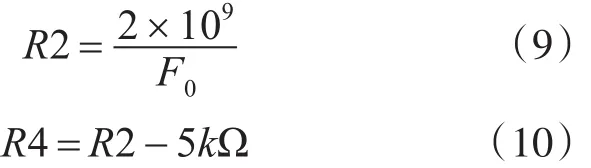
由式（3）可知，电阻R3设置调整滤波器的口若悬河质因数Q，

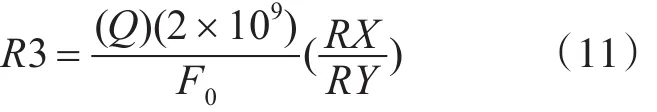
当Fc接高电平时，RX/RY取值为4/1；

当Fc接地时，RX/RY取值为1/5；

当Fc接低电平时，RX/RY取值为1/25；

电阻R1决定滤波器的增益G，R1的值与低通滤波通道的增益G成反比，且由以上公式有

当Fc接高电平时，RX/RY取值为4/1；

当Fc接地时，RX/RY取值为1/5；

当Fc接低电平时，RX/RY取值为1/25；

由式（9）～（12）可知，当低通滤波器中心频率F0确定下来以后，R2和R4的阻值就唯一的确定下来，并且在RX/RY值已知的条件下，Q值决定于R3，而系统增益G为R1与F0乘积的倒数，这样，四个外接电阻与三个系统参数F0、Q、G之间的关系也就确定了。我们只需要通过改变F0、Q、G这三个参数，就可以得到所需要的幅度谱。

4 Chebyshev高阶有源低通滤波器设计实践

当滤波器的阶数较高时，就需要通过多个滤波单元级联来实现。一般来说，止带处的特性曲线变化陡峭，因此，二阶节的Q值较大，求出的电阻值一般也比较大；而中间部分的二阶节则Q值较小，曲线平缓。合理地分配各个中心频率非常重要，它将直接影响到滤波器的结构复杂程度，甚至最终的滤波效果。

在求出各个电阻值后，不要急着将它设计成电路，可以事先通过MATHEMATIC或者是MATLAB对滤波器的频谱进行仿真［12］。观察不同的外接电阻值对整个频带的影响，以求得最佳的通带。

图3为四通道低通滤波器电路图。

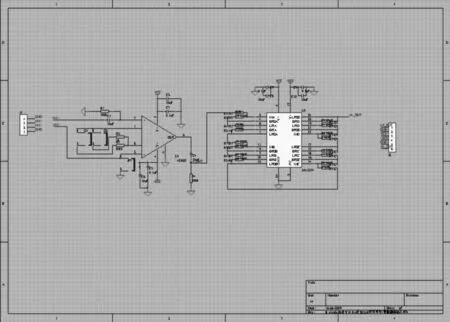
图3 四通道低通滤波器电路图

5 结语

该设计方案已应用于某型水下目标测量系统中，成功地解决了目标因环境噪声等原因引起的外部干扰而不能准确测量的难题。实际应用证明，采用连续时间集成滤波器MAX274设计和制作的Chebyshev高阶低通滤波器，其结构简单，易于设计，性能可靠，避免了传统高阶滤波器电子元件多、不宜调节的缺点。

但是值得提出的是，由于高阶滤波器滤波节数多，因而不可避免地会带来一些高噪声，这对于弱信号来说是极为不利的，在实际应用中就出现了高频测距信号不能完全滤除的现象；另外，模拟滤波器在通带范围内还会产生一定的相移，这也是实际操作过程中需要考虑的因素。