模糊一致集

李 辉，姜广浩，刘东明

(淮北师范大学数学科学学院，安徽淮北 235000)

1 研究背景

自1965年Zadeh引入模糊集的概念[1]以来，众多数学学者对于模糊数学的研究已取得了丰硕的成果，其中对模糊理想的定义就出现多种形式，本文采用其中一种模糊理想的定义方式.白仲林[2]给出了偏序集上一致偏序集的定义，使偏序集得以丰富.Yuan B[3]引入了模糊理想的概念，研究了模糊格上的模糊理想和模糊滤子.姜广浩[4]给出了偏序集上局部极大理想的定义，并探讨了局部极大理想的一些性质.肖璨[5]提出了模糊集在分配格上的一个内部刻画，给出了模糊主理想、模糊次极大理想等定义,并考察了几类模糊理想之间的关系.本文首先在一致集的基础上，结合模糊偏序集和模糊理想的相关知识，给出模糊一致集和模糊一致完备集的定义，并研究它们的相关性质.其次，引入模糊一致理想和极大模糊一致理想的概念，讨论模糊理想与模糊一致理想的关系，给出若干等价条件，并证明极大模糊一致理想的存在性.

2 预备知识

给出如下定义[1-3]：

定义2.1 (i)设X是偏序集，Y⊆X称为X的一致集，若∀x,y∈Y，存在z∈X，使得x≤z且y≤z；(ii)对偏序集上X的任意一致集都存在最小上界，则称X是一致完备的.

定义2.2 设X是非空偏序集，A:X×X→[0,1]为映射，其中[0,1]为单位闭区间，称A是X上的一个模糊偏序关系，若A满足：(i)自反性：∀x∈X，A(x,x)=1；(ii)传递性：∀x,y,z∈X，A(x,y)∧A(y,z)≤A(x,z)；(iii)反对称性：∀x,y∈X，A(x,y)>0，A(y,x)>0⟹x=y，则称偶对(X,A)为模糊偏序集，简称模糊集.

定义2.3 设(X,A)为模糊集，Y⊆X为子集，u∈X，若对∀x∈Y有A(x,u)>0，则称u为Y的一个上界，若对Y的任意上界y∈Y都有A(u,y)>0，则称u为Y的上确界；若有A(u,x)>0，则称u为Y的一个下界，若

对Y的任意下界v都有A(v,u)>0，则称u为Y的下确界.Y的上确界记为supY,用符号表示为∨Y，下确界记为infY，用符号表示为∧Y.若对∀x,y∈X，都有A(x,y)>0或A(y,x)>0，则称A为模糊全序关系，(X,A)为模糊全序集.

定义2.5 设(X,A)为模糊格，Y⊆X为子集，(i)若x∈X,y∈Y，且A(x,y)>0时，有x∈Y；(ii)若x,y∈Y，有x∨y∈Y，则称Y为模糊理想.全体模糊理想记作FIdl(L).

注2.1 若Y⊆X为模糊格(X,A)的一个模糊理想，则(Y,B)为(X,A)的模糊并半格.

3 主要结果

定义3.1 设(X,A)为模糊偏序集，Y⊆X为非空分明子集，若∀x,y∈Y，存在z∈X，使得A(x,z)>0,A(y,z)>0，则称Y为模糊集(X,A)上的一个模糊一致集，(X,A)上的全体模糊一致集记为FU(X).

例3.1 设X={a,b,c},Y={a,b}，规定A(a,c)>0,A(b,c)>0，则Y为模糊一致集.若还有A(a,b)>0或A(b,a)>0,则称(X,A)为模糊全序集.

定义3.2 若模糊集(X,A)中的每个模糊一致集都存在上确界，则称模糊集(X,A)是模糊一致完备的.若对∀Y∈FU(X)，∀x,y∈Y时x∧y,x∨y都存在，则称(X,A)为模糊一致格.

注3.1 每个模糊一致格都是模糊一致完备的，但模糊一致完备集不一定是模糊一致格.因为对∀x,y∈Y，x∧y不一定存在.

注3.2 设(X,A)为模糊一致格，则(X,A)为模糊格.

证明 设(X,A)为模糊一致完备集，Y∈FU(X)，则对∀x,y∈Y⊆X，x∧y,x∨y都存在，故(X,A)为模糊格.

上述推论反过来不成立，即若(X,A)为模糊格，但(X,A)未必为模糊一致格.

例3.2 在图1中，设模糊格L={a,b,c,d,e}，I={a,b,c,d}为模糊一致集，但a∨b=e∉I,即I不为模糊一致格.

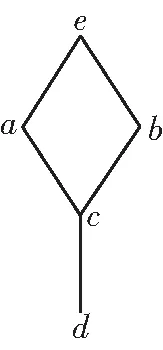
图1 例3.2示意图

定理3.1 设(X,A)为模糊格，D,F∈FU(X)，若D∩F≠∅，则D∩F为模糊一致集.

证明 设(X,A)为模糊格，D,F∈FU(X)，令W=D∩F，由于(X,A)为模糊格，故对∀x,y∈X，x∧y都存在.对∀x,y∈W，即x,y∈D∩F，可知x,y∈D且x,y∈F.由D,F为模糊一致集，故存在z∈X使得A(x,z)>0,A(y,z)>0，故W为模糊一致集，即D∩F为模糊一致集.

定义3.3 设(X,A)为模糊偏序集，若(1)I∈FU(X)；(ii)若x∈X,y∈I，当A(x,y)>0时，有x∈I，则称I为模糊集(X,A)的模糊一致理想.全体模糊一致理想记作FUIdl(L).

定理3.2 设(X,A)为模糊格，若I∈FIdl(L)，则I∈FUIdl(L).

证明 设(X,A)为模糊格，I∈FIdl(L)，x∈X,y∈I，A(x,y)>0有x∈I，且x,y∈Y，有x∨y∈Y，令z=x∨y，故z∈I⊆X,又有A(x,z)>0,A(y,z)>0，即对∀x,y∈I时，存在z∈X,使得A(x,z)>0,A(y,z)>0，故I为模糊一致理想.

推论3.2 定理3.2的逆定理不成立，即I为模糊一致理想，但I未必是模糊理想.

例如在图1中I为模糊一致理想，但不是模糊理想.因为虽然a∈I,b∈I，但a∨b∉I，故I不为模糊理想.

在何条件下模糊理想是模糊一致理想呢？下面给出一个等价条件.

命题3.1 设(X,A)为模糊一致完备集，I⊆X，则I为模糊一致理想⟺I为模糊理想.

证明 必要性证明.设(X,A)为模糊一致完备集，I为其上的一个模糊一致理想.∀x∈X,y∈I,A(x,y)>0，有x∈I，又由(X,A)模糊一致完备，故x∨y存在，且x∨y∈I,故I为模糊理想.

充分性证明.设I∈FIdl(L),由定理3.2可知I∈FUIdl(L).故充分性成立.

定理3.3 设(X,A)为模糊集，Y为其上的模糊一致集，则↓Y={x∈X:∃y∈Y,A(x,y)>0}为一个模糊一致理想.

证明 (i)设c∈↓Y，d∈X，使得A(d,c)>0，由Y为模糊一致集，故存在x∈Y使得A(c,x)>0，由传递性A(d,x)>0，可知d∈↓Y.

(ii)设x,y∈↓Y，于是存在a,b∈Y，使得A(x,a)>0,A(y,b)>0，进而A(x,a∨b)>0，A(y,a∨b)>0，令z=a∨b，于是对任意的x,y∈↓Y，存在z∈X,使得A(x,z)>0,A(y,z)>0，故↓Y为模糊一致集.综上↓Y为一个模糊一致理想.

注3.3 若将定理3.3中(X,A)为模糊集改为模糊一致完备集，其余条件不变，则↓Y为一个模糊理想.这是因为在证明(ii)中若(X,A)为模糊一致完备，则z∈↓Y，故↓Y为模糊理想.

命题3.2 设(X,A)为模糊格，Y为(X,A)上的一个模糊一致理想，则↓Y⊆↓supY.

证明 由Y为模糊一致理想，故对∀x,y∈Y，∃z∈X，使得A(x,z)>0，A(y,z)>0.取z=supY,即∀x,y∈Y，x,y∈↓supY，故↓Y⊆↓supY.

命题3.3 设L为模糊偏序集，Y为它的模糊一致理想，则对∀x∈Y,有Y=∪↓x，其中↓x为模糊主理想.

定理3.4 设Y是模糊偏序集(X,A)的一个模糊一致理想，且x∈XY，令I=∪{↓(x∨a):a∈Y}，则I是(X,A)的一个模糊理想，且Y⊆I.

证明 (i)任取b1,b2∈I，x∈XY，则存在a1,a2∈Y，使得A(b1,x∨a1)>0，A(b2,x∨a2)>0，故A(b1∨b2,(x∨a1)∨(x∨a2))>0，即A(b1∨b2,x∨(a1∨a2))>0.令z=x∨(a1∨a2)，则b1∨b2∈↓z.

(ii)下证z∈I.事实上，对任意a∈Y，有I=∪(↓(x∨a))=↓(∪(x∨a)).对任意a1,a2∈Y，有x∨(a1∨a2)∈∪(x∨a)，即z∈∪(x∨a)，进而z∈↓(∪(x∨a))，故z∈I.因此，对任意b1,b2∈I，b1∨b2∈I,故I为一个模糊理想.

定义3.4 设(X,A)为模糊偏序集，Y为(X,A)中的模糊一致理想，若∀x∈X，使得Y在不包含x的模糊一致理想中极大，则称Y为(X,A)的一个极大模糊一致理想.即若x∉Y,x∈I∈FU(X)且Y⊆I，则Y=I.

定理3.5 设(X,A)为模糊格，Y为(X,A)的模糊一致理想，对∀a∉Y，则必存在关于a的极大模糊一致理想M，使得a∉M且Y⊆M.

注3.4 在图1中{a,b,c,d}，{a,c,d}，{b,c,d}均为关于元素e的极大模糊一致理想，{d}是关于元素c的极大模糊一致理想，但{c,d}不为极大模糊一致理想，因为{c,d}包含于{a,c,d}和{b,c,d}中.

注3.5 根据模糊一致集的定义，若z∉Y，则模糊一致理想Y是关于z的极大模糊一致理想；若z∈Y，则模糊一致理想Y是模糊理想.