选好例题 注重实效 解法自然

☉山东省乳山市第一中学 滕建峰

在近几年的高考题与模拟题中，经常会碰到求解多变元代数式的最值或取值范围问题，特别是双变元代数式的最值或取值范围问题.此类问题往往难度较大，思维方式多变，方法有时也多样.下面结合一道双变元代数式的最值问题来加以实例剖析，结合多维角度切入，达到殊途同归.

例题 （2018届江苏省南师大附中、淮阴中学、海门中学、天一中学高三2月联考·14）已知a>1，b>2，则的最小值为____.

分析：这是一道双变元在已知条件下代数式的最值问题，这类问题一直受备命题者的青睐.涉及此类双变元代数式在满足限制条件下的取值范围问题，可以通过换元思维、求导方法、待定系数法，以及几何模型法等思维角度来处理，解决的关系如何转化对应代数式中的根式，加以合理转化与应用，思维多样，方法各异.通过认真审视这道试卷，在不同视角下，得到了该题的不同解题思维与对应的精彩解法.

角度1——换元法1

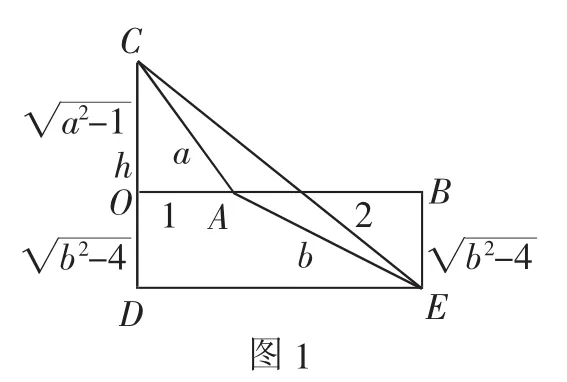
解法7：由于a>1，b>2，如图2，构造平面几何模型，设AB⊥AC，AB⊥BD，且|AC|=1，|BD|=2，连接CD交AB于点F，设|CF|=a，|FD|=b，过C作CE⊥BD交DB的延长线于点E，设∠DCE=θ.

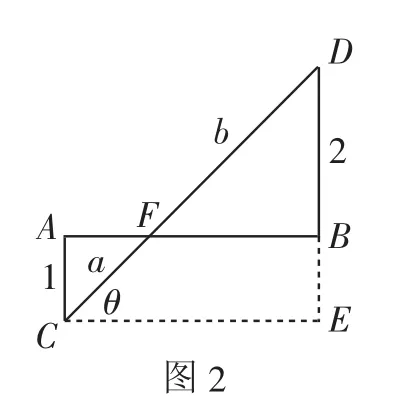
点评：解法1与解法2均是通过引入参数m，n，根据基本不等式或柯西不等式来转化，进而结合基本不等式来确定最小值问题；解法3与解法4均利用基本不等式加以转化，再分别从求导法或待定系数法来确定相应的关系式的最大值，从而得以确定双变元代数式的最小值问题；解法5利用柯西不等式来转化分母中的根式，再通过换元思维，结合基本不等式来确定双变元代数式的最小值问题，回归不等式本质；而解法6与解法7利用不同的平面几何概型的建立，通过两个直角三角形的关系，结合三角形的性质或三角函数的最值，可以达到“秒杀”的效果，只是对应的不同的几何模型的构造具有非常大的想象力与创新力.

通过“一题多解”可以将主干知识进行“串联”，同时“并联”起数学思想方法和核心素养，开拓学生的解题视野，有效促进学生思维品质的改善和创新发展能力的提升，体验到数学的乐趣，收获成功的喜悦，增强学习数学的兴趣和信心.