一题四解，妙求范围

☉江苏省宜兴中学 杨志刚

二次函数衔接起初中与高中数学，是高中数学中的重要内容之一，也是各类考题中比较热衷的问题背景之一，已经成为高考命题的高频考点之一.特别是二次函数与方程的交汇，二次函数与绝对值的交汇等问题，往往整合初中与高中知识，加以有机融合与拓展，这就更需要我们多加研究，以便了解和掌握二次函数的图像与性质，总结相应的解题规律，拓展思维.同一数学问题，可以从多方位、多角度、多层次入手，就会得到多种解题思路和方法，从而提高对数学知识的理解和掌握，同时也提升数学解题能力，培养优良的数学素养.

例题（江苏省某市4月联考·14）若方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，且x1＜x2＜x3＜x4，则2（x4-x1）+（x3-x2）的取值范围是______.

分析：本题主要考查二次函数的图像与性质，绝对值及其应用，函数与方程，函数的零点，函数的图像与性质，导数及其应用等众多的知识.通过导数、三角函数、线性规划及柯西不等式等相关知识的融合，采用不同的切入点，处理方法各异，均可达到目的.

思路1：结合二次函数的对称性得到x1+x4=x2+x3=2，通过引入参数t使得x1·x4=-1-t，x2·x3=-1+（t0＜t＜2），进而得到通过构造函数结合求导，利用函数的单调性来确定相应最值问题，进而确定代数式的取值范围.

解法1：因为方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，x1＜x2＜x3＜x4，所以x1+x4=x2+x3=2，x1·x4=-1-t，x·2x3=-1+（t0＜t＜2）.

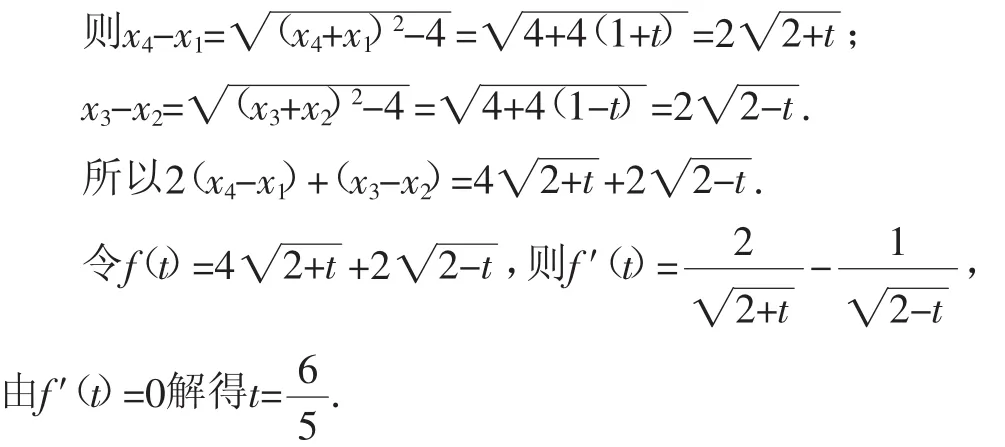
所以2（x4-x）1+（x3-x2）的取值范围是

思路2：结合二次函数的对称性得到x1+x4=x2+x3=2，通过引入参数t使得x1·x4=-1-t，x2·x3=-1+（t0＜t＜2），进而得到通过三角换元结合三角关系式的转化，利用三角函数的图像与性质来确定代数式的取值范围.

解法2：因为方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，x1＜x2＜x3＜x4，所以x1+x4=x2+x3=2，x1·x4=-1-t，x2·x3=-1+（t0＜t＜2）.

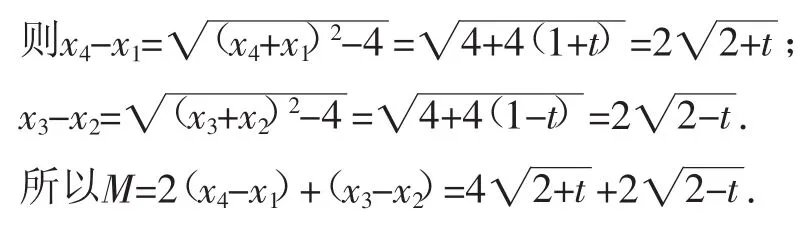
所以2（x4-x1）+（x3-x2）的取值范围是

思路3：结合二次函数的对称性得到x1+x4=x2+x3=2，通过引入参数t使得x1·x4=-1-t，x2·x3=-1+（t0＜t＜2），进而得到通过引入参数建立对应的约束条件，利用线性规划，结合目标函数z=4m+2n在确定平面区域内的取值情况来确定代数式的取值范围.

解法3：因为方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，x1＜x2＜x3＜x4，所以x1+x4=x2+x3=2，x1·x4=-1-t，x·2x3=-1+（t0＜t＜2）.

对于目标函数z=4m+2n，结合图像，过点A（2，0）时，zmin=8；当直线z=4m+2n与圆m2+n2=4在第一象限相切时，此时有可得

所以2（x4-x1）+（x3-x2）的取值范围是

思路4：结合二次函数的对称性得到x1+x4=x2+x3=2，通过引入参数t使得x1·x4=-1-t，x·2x3=-1+（t0＜t＜2），进而得到2（x4-结合柯西不等式确定该关系式的上限，再利用0＜t＜2在两极端情况时的取值，通过连续函数的取值情况来确定代数式的取值范围.

解法4：因为方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，x1＜x2＜x3＜x4，所以x1+x4=x2+x3=2，x1·x4=-1-t，x2·x3=-1+（t0＜t＜2）.

所以2（x4-x1）+（x3-x2）的取值范围是

其实，解题的思维一定不能单一，具体解题时应该以常规方法优先，然后逐步优化，当面临较为特殊的结构时，往往多思考就有更为巧妙的方法.因而，当我们解完一道题以后，要不断领悟反思，多角度切入进行深度挖掘，从而达到触类旁通、一题多解的效果.通过典型实例的一题多解，可以使得我们的解题思路更加开阔，数学知识的掌握更加熟练，同时思维拓展，妙法顿生，提高解题速度，培养发散思维能力，有助于激发我们学习的主动性、积极性和趣味性，从而全面提高我们的知识水平和思维能力.