数学运算核心素养在解题体验中“落地”——以2018年江苏卷第13题为例

☉江苏省如东高级中学 郭 伟

数学运算核心素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，它包含了：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等数学能力.众所周知，数学解题活动需要通过计算、推理来实现，因此，解题教学是发展学生数学运算核心素养的有效手段.显然，那种“就题论题”、“题海战术”式的解题教学是无法承载发展核心素养的重任，那么，数学运算如何在解题教学中“落地”呢？

一、问题剖析：体验运算之势

题目（2018年江苏卷第13题）在△ABC中，角A、B、C所对的边分别为a、b、c，∠ABC=120°，∠ABC的平分线BD交AC于点D，且BD=1，则4a+c的最小值为______.

剖析：如图1，此题以三角形边角之间的关系为问题背景，考查学生综合运用各种知识解三角形的能力.由于本题要求的结果是4a+c的最小值，而最值的一般套路往往是转化为函数或基本不等式来求解，因此，本题的解题方向是明确的，解题的难点在于找到一组关于a、c的等量关系式，这其实就是在考查学生的运算能力，即把题目条件中的几何关系式转化为代数式，然后通过运算来获得关于a、c的等式.我们把题目中的几何条件与可能对应的代数表示用一张表格列出来，这样容易找到解题的突破口.

图1

几何条件 可能的代数表示∠ABC=120° 用向量的夹角表示、用余弦定理或正弦定理表示∠ABC的平分线交AC于D用内角平分线定理表示、用向量共线定理表示、利用面积关系进行表示BD=1 作为三角形的一条边，利用余弦定理、正弦定理的表示

通过上述表格分析，本题有两种解答视角：几何与向量.每种视角又可以细分为若干种方法.通过对问题进行多重视角的分析与解答，学生经历不同的运算表示，从而使学生的数学运算核心素养得到充分的发展.

二、几何视角：体验运算之巧

在数学知识中，几何关系虽然直观，但其内部蕴含的逻辑关系却比较复杂，往往相互依赖，共生共存，这就给问题的解决提供了多重思维视角.立足不同几何关系获得的解题思路，在运算上看似大相径庭，但到最后都会殊途同归，让人感到异曲同工之妙.

1.根据面积表示等量关系

角平分线BD把△ABC分成两部分，因此整个三角形的面积就是两个小三角形面积之和.如果能够把这个两个小三角形面积表示出来，就能得到一个等量关系.

解法一：因为S△ABC=S△ABD+S△BCD，所以acsin120°=化简得，ac=c+a⇒所以4a+c=（4a+c）当且仅当c=2a，即a=，c=3时等号成立，所以4a+c的最小值为9.

2.结合内角平分线性质利用正弦定理表示等量关系

解法二：因为BD是角平分线，因此三角形满足内角平分线的性质，即于是AD与DC就可以用三角形的边a，b，c表示出来，接下去就可以利用正弦定理列出边角之间的等量关系.

3.结合内角平分线性质利用余弦定理表示等量关系

解法三：其实，还可以用余弦定理表示边角之间的等量关系.在△ABD与△CBD中，利用余弦定理得到因为所以把两式相除得化简得（a+c）（a-c）=（a-c）ac，即a=c或ac=c+a.

若a=c，因为BD=1，所以a=c=2，则4a+c=10；若ac=c+a，后续的做法和前面一致.最后得到4a+c的最小值为9.

4.利用图形隐藏的几何性质表示等量关系

解法四：如图2，过D点作DE∥AB交BC于E.这样作辅助线的好处有两点，一是可以利用平行相似比列等式，二是把分散在不同位置的几何性关系集中到一处，解法更加简洁.

图2

显然，有∠DBE=∠BDE=60°，所以△BDE是正三角形，则BD=DE=EB=1，EC=a-1.由化简得ac=c+a.

除了上述辅助线的画法，我们还有其他的画法，如图3所示，过A作AE∥BC交BD延长线于点E.所以∠E=∠CBD=∠ABD=60°，所以∠BAC=60°，故△ABE为等边三角形，所以AE=BE=AB=c.因为BD=1，则DE=c-1.由AE∥BC得

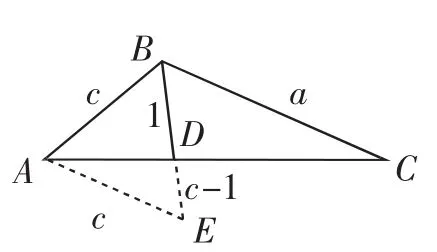
图3

综上，尽管考虑问题是视角不同，运算的式子不同，最后都能得到ac=c+a这一关键等式，“条条大路通罗马”，这就是运算的奥妙所在.

三、向量视角：体验运算之法

向量是沟通代数、几何、三角的桥梁，是重要的解题工具.相比于一般的几何法，向量法的优点在于运算套路基本固定.它一般遵循两大运算法则：一是基向量法则，二是坐标运算法则.

1.运用基向量运算借助共线定理表示等量关系

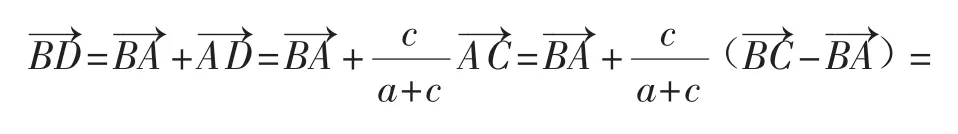
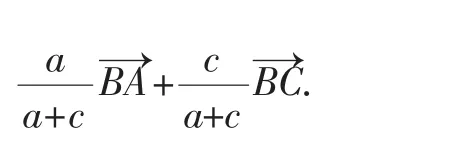
2.运用坐标运算借助共线定理表示等量关系如图4，以B为原点，BC为x轴建立直角坐标系，

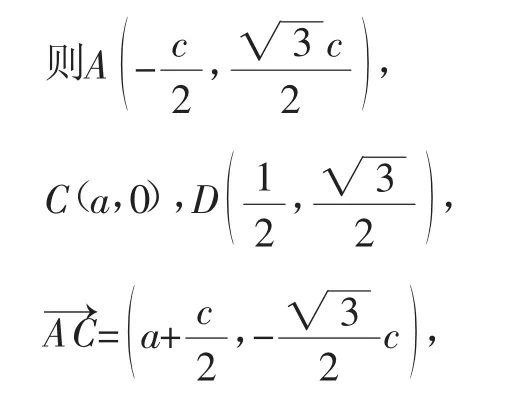
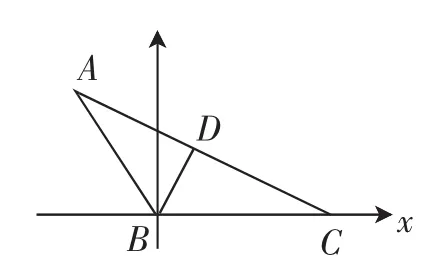
图4

四、拓展变式：体验运算之本

题目的拓展与变式对于发展学生的运算核心素养具有重要的作用，在类比中提炼出某类问题的通解通法，形成程序化的解题策略；在对比中完善和发展数学运算能力，培养科学严谨的理性精神，这才是运算的根本价值之所在.本题的运算主要涉及到“角平分线性质”与“基本不等式求最值”两个知识点，因此，可以围绕着这两个方面进行拓展与变式.

【题组一】角平分线性质的应用

变式1：如图5，在△ABC中，角A、B、C所对的边分别为a、b、c，且a2+c2=b2-ac，∠BAC的平分线AD交BC于点D，1，则cosC=______.

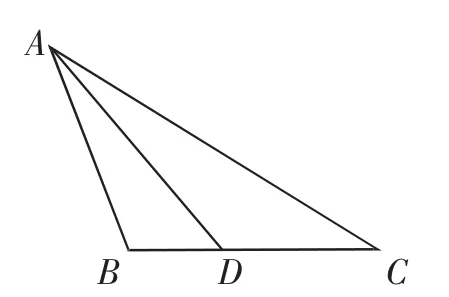
图5

变式2：在△ABC中，AD是∠A的平分线，若则AD的取值范围是______.

变式3：在△ABC中，角A、B、C所对的边分别为a、b、c，且，∠A的平分线交BC于D，且则S△ABC=______.

意图：通过多重视角挖掘角平分线的几何性质，把几何性质代数化，列出等量关系，通过运算获得相关的结论，从而掌握这一类问题的解题套路，提升学生的运算转化能力.

【题组二】基本不等式的应用

拓展1：已知A，B，C是平面上任意三点，BC=a，CA=b，AB=c，则的最小值是______.

解析：由b+c≥a，得

拓展2：已知正数x，y满足的最小值为______.

解析：由得到x+y=xy，则所以9x+4y=（9x+

意图：上述两道求最值的拓展性问题用到了相对比较复杂的运算技巧，这也是学生在运用基本不等式求最值时需要掌握的.通过问题的解答，进一步提升学生数学运算的核心素养.

学生通过不断的解题体验，获得情感体验，激活其数学思维，数学运算的技巧在情感交融状态中达到一种理解和心领神会，从而使数学运算核心素养的构建由肤浅逐步走向深入.