一道三角形面积最值题的多解剖析

☉安徽省临泉一中 张凯华

解三角形主要通过对任意三角形边角关系的探索，掌握正弦定理、余弦定理，并能利用它们解决一些简单三角形度量问题及一些与测量和计算有关的实际问题.该部分是每年高考中的基本考点之一，大都运算量大、公式应用多，这就要求我们不仅具有较高的运算水平、较强的运算能力和较大的记忆能力，还应善于审题，采用相应的策略，优化过程.特别对于解三角形中的最值问题，备受命题者青睐，更是各类考试中的热点题型.下面结合一道三角形面积的最值题加以多解剖析.

例题在△ABC中，若AB=1，tanB=2tanC，则△ABC面积的最大值是______.

分析：本题给出三角形的一边AB=c=1，以及角B，C的正切值的三角关系式，解决问题的关键就是如何把关系式tanB=2tanC加以巧妙转化，可以利用同角三角函数基本关系式、直角三角形中的边角关系等加以转化，转化为涉及三角形的相关边以及角的正弦值或余弦值，再代入三角形的面积公式，利用基本不等式法、三角函数的图像与性质法等来确定对应的最值即可，进而达到求解问题的目的.

结合题目条件tanB=2tanC转化为正、余弦的关系式，结合正弦定理与余弦定理转化为边的关系式，得以确定再由条件和余弦定理求出cosB，由同角三角函数基本关系式可得sinB的值，代入三角形的面积公式，利用含参数a的关系式的基本不等式法来确定三角形面积的最值即可.

解法1：由tanB=2tanC，可得则有sinBcosC=2cosBsinC.

而由余弦定理可得：

根据条件过A点作AD⊥BC交BC于点D，引入参数h=AD，把BD表示成h的关系式，同时利用条件把BC也表示成h的关系式，代入三角形的面积公式，利用含参数h的关系式的基本不等式法来确定三角形面积的最值即可.

解法2：过A点作AD⊥BC交BC于点D，设AD=h，则知0＜h＜1.

根据条件过A点作AD⊥BC交BC于点D，把AD、BC表示成角B的三角关系式，同时利用条件把CD也表示成角B的三角关系式，代入三角形的面积公式，结合二倍角公式，利用三角函数的图像与性质来确定三角形面积的最值即可.

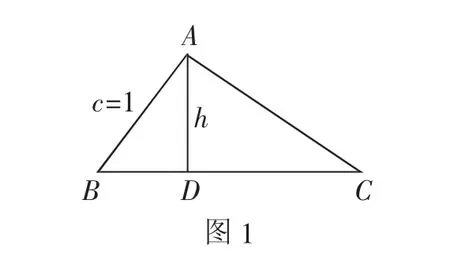
解法3：如图1，过A点作AD⊥BC交BC于点D.

而AB=c=1，

可得AD=sinB，BD=cosB.

根据条件过A点作AD⊥BC交BC于点D，引入参数x=BD，把AD表示成x的关系式，同时利用条件把CD也表示成x的关系式，代入三角形的面积公式，利用含参数x的关系式的基本不等式法来确定三角形面积的最值即可.

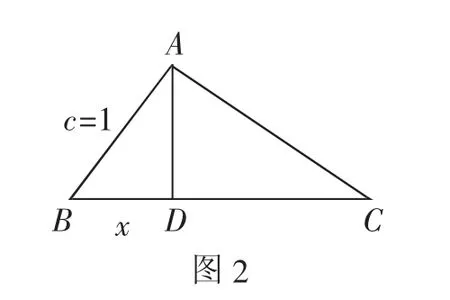
解法4：如图2，过A点作AD⊥BC交BC于点D，而AB=c=1，设BD=x，则知0＜x＜1.

结合题目条件tanB=2tanC转化为正、余弦的关系式，结合两角和的正弦公式加以合理转化与应用，同时利用三角形的内角和公式与诱导公式加以转化得到sinA=3cosBsinC，结合正弦定理转化为a=3cosB，代入三角形的面积公式，结合二倍角公式，利用三角函数的图像与性质来确定三角形面积的最值即可.

解法5：由tanB=2tanC，可得

则有sinBcosC=2cosBsinC，

可得sinBcosC+cosBsinC=3cosBsinC，

即sin（B+C）=3cosBsinC，亦即sinA=3cosBsinC，

结合正弦定理可得a=3ccosB=3cosB（c=AB=1）.

点评：在解决三角形问题中，比较常见的思维方法就是正弦定理与余弦定理，这也是解决此类问题的典型方法.而涉及三角形的面积的最值问题，关键是通过代数运算，将几何模型代数化，利用正弦定理、余弦定理、三角相关公式等来转化与解题，利用基本不等式、三角函数的图像与性质等来确定最值问题.

通过从多个不同角度来处理，巧妙地把该题的底蕴充分挖掘出来，多角度出发，多方面求解，真正体现对数学知识的融会贯通，充分展现知识的交汇与综合，达到提升能力，拓展应用的目的.进而真正达到在学中“悟”，在“悟”中不断提升解题技能.正如我国著名数学家苏步青先生所言：“学习数学要多做习题，边做边思索，先知其然，然后知其所以然.”