圆柱工件表面缺陷视觉检测补偿方法研究
2018-10-22孟繁明王道档郭天太
孔 明,孟繁明,王道档,赵 军,刘 维,郭天太
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
圆柱工件是船舶、汽车、武器和航空航天等众多机械制造领域中必不可少的零件之一,圆柱工件的质量也是机械的使用寿命、安全性和可靠性等指标好坏的关键因素.其中,工件的表面质量也是国内外厂家所关心的重要指标之一.受铸件工艺、设计技术以及运输刮碰等客观因素的影响,圆柱工件表面通常会有裂纹、气孔、缝隙、白点、污渍、擦伤、锈迹等缺陷,严重降低了后续产品的性能.所以对工件表面缺陷的检测是必不可少的[1].
工件表面缺陷的检测方法主要有目视检测、超声检测、磁粉检测、渗透检测、涡流检测以及光电检测[2]等方法.其中人工目视检测的方式,检测效率低,成本提高,且缺乏可靠性和规范性;超声检测对平面型缺陷敏感但难以检测细小裂纹;磁粉检测限于铁磁材料,在检测后要进行工件退磁处理;渗透检测设备简便,适用所有材料,但检测后需要清洁工作;涡流检测限于导体材料,需要检测标准.以上检测方法均适用于抽检,不适合流水线大批量检测.随着制造业的大规模、批量化生产,尤其在精密制造领域,基于机器视觉的检测方式以其自动化程度高、识别率好,且是非接触测量等优点,逐渐成为在线检测的主流方法.
在圆柱工件外观缺陷检测中,由于工件表面是曲面,所以缺陷的多变性使其与平面的缺陷检测存在一些差异.宋宇宁[3]等人研究了内衬套的缺陷检测,使用低角度照明的方式,利用图像形态学和GrabGut分割算法检测工件表面缺陷.该方法检测时需在暗箱里进行,不适合真实的工业现场.孙雪晨[4]等人利用邻域加权分割对凸轮轴表面缺陷提取,该测量系统搭建在生产流水线两侧,利用流水线停留时凸轮轴自身的旋转采集图像,进行缺陷检测,但是在流水线上,凸轮轴的旋转需要电机带动,如果每个凸轮轴都搭配一个旋转装置无疑增加许多成本,且凸轮轴的旋转时间受算法限制不能过快,所以该方法在实时检测时的效率不高.张静[5]等人采用左右2个条形光源照明,将局部图形空间纹理模式与图像强度对比度相结合,对缺陷检测的不同种类有较好的鲁棒性,提高了检测微小缺陷的准确性,但由于没有考虑缺陷在曲面的补偿问题,所以在单次采集检测时,会出现漏检、错判的情况.
本文围绕上述问题展开了分析研究,利用理想小孔成像模型,通过对模型的畸变标定,得到工件曲面不同位置的点像素与实际尺寸的对应关系曲线.搭建流水线检测系统,利用4个CMOS相机采集圆柱工件图像,通过单次采集即可判断缺陷是否合格.该检测系统可以实时检测缺陷,大大提高了出场效率和质量.
1 检测原理
1.1 系统结构
根据圆柱工件生产流水线的特点,将检测系统设计在流水线两端,在检测到工件出现后,采集工件图像并进行检测分拣,实现了工件流水线上的实时检测.检测系统由光源照明、图像采集和图像处理三部分组成,其结构示意图如图1.

图1 检测系统结构图Figure 1 Structure of detection system
由于圆柱工件的表面是曲面,所以照明方式会影响检测的准确度[5].采用平行背光照射时,目标轮廓比较突出,但正面亮度不够,无法分辨缺陷所在.正面平行光照射时,圆柱工件中线部分形成高亮,边缘部分出现模糊,丢失待检测缺陷的信息.考虑到工业现场环境,本文采用日光灯照明,环形光源置于工件底部侧面照明,这样工件两侧轮廓分明,缺陷在靠近轮廓边缘时,会增强缺陷信息强度,更利于检测.
采集图像时,相机一次可获得圆柱工件整圈表面三分之一左右,由于缺陷在图像边缘时的信息不完整,所以一次采集检测的范围是工件圆周的100°左右,所以本系统使用4个CMOS采集图像,这样可以一次采集到圆周工件的整周.通过COMS相机采集图像,进入图像处理步骤.
系统的图像处理共分为四步,分别是预处理、提取缺陷、缺陷几何测量以及分拣[6-9].其中预处理部分主要是滤波去噪,本文采用的滤波方法是高斯滤波.通过对预处理的图像进行缺陷检测后,将得到的缺陷信息代入到经过修正的小孔透视模型,根据处理结果,实现合格与不合格的检测判定.
1.2 基于小孔模型的补偿模型
根据照相机透镜成像的原理,建立检测的小孔成像模型.图2是检测系统的俯视模型,将检测系统分成三部分,分别为:待测圆柱工件,相机透镜和成像平面.
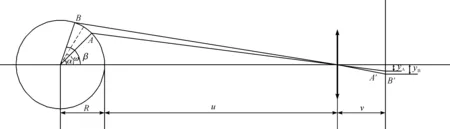
图2 小孔摄像机投影模型Figure 2 Pinhole camera projection model
根据小孔成像的投影模型[10],可以知道圆柱工件擦痕的端点A、B在像平面成像位置A′和B′,根据相似三角形的几何模型,可以得到点A,B与光轴的距离在像平面对应的yA和yB.对应关系式如下:

(1)
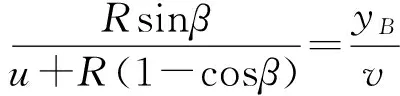
(2)
式(1)(2)中:α和β分别是擦痕端点A、B和工件圆心的连线与光轴的夹角,圆柱工件的半径为R,工件与透镜之间的距离为u,透镜与像平面之间的距离为v.
由模型可看出,擦痕端点A、B和工件的圆心构成了一个扇形,那么该扇形对应的圆心角、擦痕中点和工件圆心的连线与光轴的夹角ω及擦痕端点A、B和工件圆心的连线与光轴的夹角α和β四个角度之间存在一定的对应关系,假设擦痕AB的长度为L,那么这种关系可表示为:

(3)

(4)
显然,擦痕AB在像平面对应的长度L′为
L′=yB-yA.
(5)
将式(1)、(2)、(3)、(4)代入式(5),可以的得到:
L′=
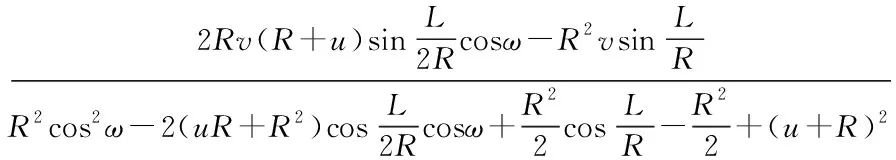
(6)
同理,擦痕中点对应在像平面像上,与光轴之间的距离V为
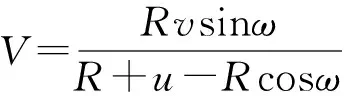
(7)
由于L′和V都是擦痕对应在像平面的实际长度,如果想知道擦痕对应在像平面的像素点位置和个数,需要要做进一步处理.本文所建立的小孔成像模型是理想状态下的模型,在实际中,摄像机光学系统并不能完全符合小孔成像模型,此外还存在加工误差和装配误差,使得曲面在摄像机图像平面上所成的像与理想成像之间存在光学畸变[11].在修正小孔成像模型时,我们认为是像素的大小存在畸变,所以通过标定来修正像素大小.
工件擦痕AB在像平面的像素点个数
N=L′/K.
(8)
理论上每像素点对应的实际尺寸

(9)
工件擦痕AB的中间在像平面的像素点位置
a=V/K′+M.
(10)
式(9)(10)中,M为像平面中点的像素点位置,K和K′为修正后的像素大小.b为修正后的小孔成像模型中的每像素点对应的实际尺寸,a为工件擦痕在像平面上成像的像素点位置.
在绘制理论曲线时,将待标定的像素大小K和K′暂时设为1,M设为0,式(6)和式(7)中ω的取值范围是-50°~+50°,每5°取一点,擦痕实际尺寸L分别设为2 mm、4 mm和8 mm.根据模型计算得到擦痕的旋转角度与每个像素点对应的实际尺寸的理论关系,如图3.以及擦痕中点在像平面的位置与每个像素点对应的实际尺寸的理论关系,如图4.三条标定前的曲线高度重合,差值小于0.1,验证了模型的正确性.

图3 擦痕在不同角度时每像素点对应的实际尺寸Figure 3 Actual size per pixel of the scratch at different angles
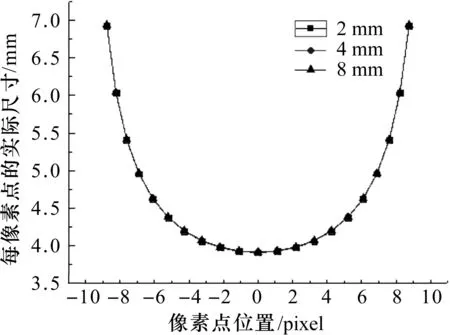
图4 擦痕在不同像素点位置时每像素点对应的实际尺寸Figure 3 Actual size per pixel of the scratch in different pixel positions
2 标定与拟合
为验证模型的可行性,在三坐标平台上搭建实验装置如图5.本文实验采用柱形瓶子模拟圆柱工件,插在转台上,分别制作网格长度为2 mm、4 mm和8 mm的棋盘格标定纸,贴在瓶子周围.环形光源置于瓶子底部.选用SONY公司的FL3-88S2C型号COMS相机,有效像素h×v为1 048×1 328.相机对准瓶子中线,采集标定纸图像.

图5 试验系统实物装置Figure 5 Experimental system
采集不同尺寸的棋盘格图像前,需要保证中心目标方块的中线与相机屏幕的竖直中线重合,作为目标方块正对相机时的图像.棋盘格图像在预处理后,目标方块的左右边缘所在像素点位置的均值,分别距离相机屏幕左右两侧的像素点个数相等或差值小于5个像素点,即认为此时目标方块的位置在屏幕的中间.对准图如图6.

图6 目标方块对准图Figure 6 Target square alignment diagram
此时的图像认为是0°图像,然后转动底部转台,每次旋转5°,左右各10次,得到中心方块在-50°~+50°的图像.
图像处理的流程图如图7,首先对采集的图像预处理,包括灰度化、高斯滤波和二值化.然后,为方便处理,截取有意义的区域.最后,检测目标方块的位置和长度.
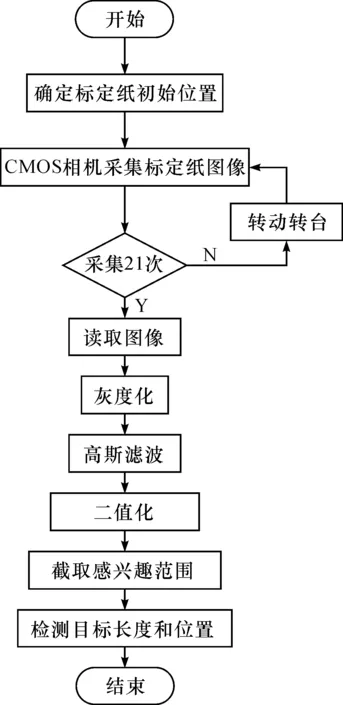
图7 像素点采集流程图Figure 7 Pixel point acquisition flow chart
处理COMS相机采集的图像,目标方块旋转不同角度,根据小孔成像模型,可以计算得到其旋转度数与每像素点对应的实际尺寸理论值.调整式(8)中K值,得到8 mm、4 mm和2 mm标定纸的旋转角度与每像素点对应的实际尺寸的测量与理论图,如图8.已知K值,调整K′,得到8 mm、4 mm和2 mm方格在像平面的像素点位置与每像素点对应的实际尺寸测量与理论关系,如图9.
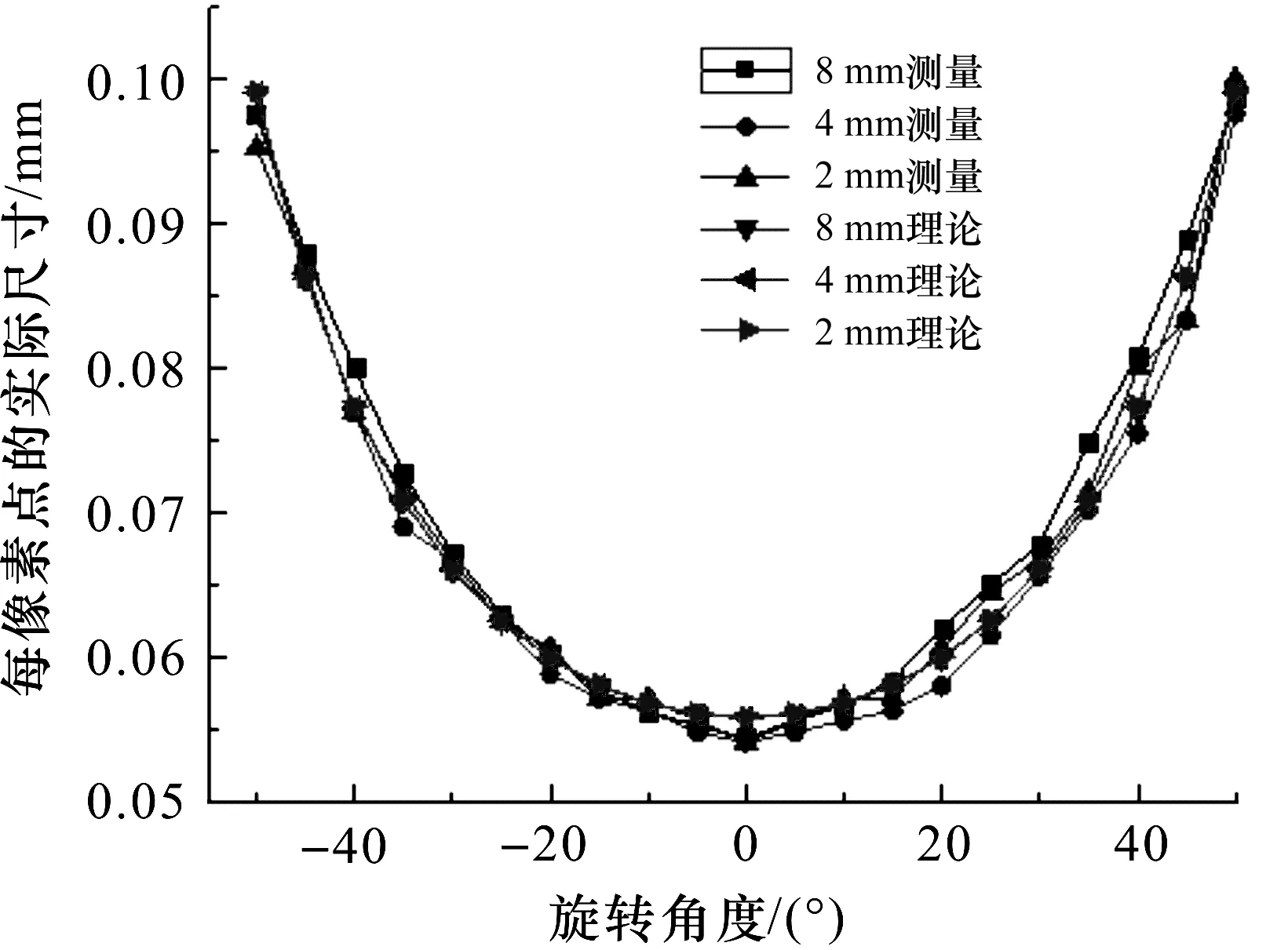
图8 旋转角度与每像素点对应的实际尺寸测量与理论关系Figure 8 Measurement and theoretical relationship between the rotation angle and the actual dimension corresponding to each pixel point

图9 方块位置与每像素点对应的实际尺寸测量与理论关系Figure 9 Measurement and theoretical relationship between the square position and the actual size per pixel
根据标定出来的K和K′值,代入模型计算出方块在像平面的像素点位置与每像素点对应的实际尺寸关系.使用傅里叶级数拟合理论曲线,得到拟合方程:
y=2.27×109-3.398×109cos(9.794×10-5x)-
2.213×108sin(9.794×10-5x)+1.351×
109cos(2×9.794×10-5x)+1.767×
108sin(2×9.794×10-5x)-2.227×108cos
(3×9.794×10-5x)-4.402×107sin(3×9.794
×10-5x).
(11)
图10为方程曲线.在拟合傅里叶方程时,根据拟合参数调整项数个数,最终项数个数为3,其中拟合后的参数如表1.可以看出,拟合的结果很好.
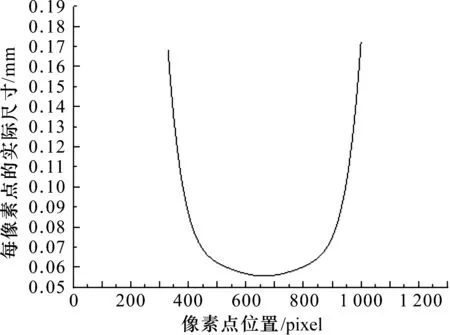
图10 傅里叶拟合曲线Figure 10 Fourier fitting curve

和方差均方差误差决定系数6.436×10-63.869×10-40.999 2
3 测量研究
为验证理论模型的正确性,本文采用一条10 mm的线段代替擦痕,采集擦痕在不同位置时的图像,通过图像处理的方法得到擦痕的参数,滤波后的二值化图像如图11所示,通过拟合关系曲线计算擦痕的理论长度.其中在采集图像时,步骤与标定时的采集方法相同,正面采集一次后,旋转转台,左右各采集10次,共采集21次图像.

图11 滤波后的检测图像Figure 11 Filtered image detection
图像处理得到擦痕的相关参数后,用三种方法计算擦痕的理论长度.中点替代法:将擦痕中点的像素点位置带入拟合方程(11),得到该位置每像素点代表的实际尺寸,认为擦痕每像素点的实际尺寸都是该值,用带入方程后得到的值乘擦痕像素点个数,即为擦痕的理论长度.积分法:将图像处理检测出来的擦痕首尾两端像素点位置作为端点,求方程(11)在此区间的定积分,即为积分法得到的擦痕理论长度.传统方法[4]:没有做曲面补偿的传统检测方法一般只采集缺陷的正面,即缺陷在圆柱工件整圈约六分之一范围内左右,认为缺陷在不同位置时每个像素点代表的实际尺寸是一样的,即用像素点个数乘每个像素点代表的实际尺寸.三种方法计算得到的擦痕理论长度如图12.
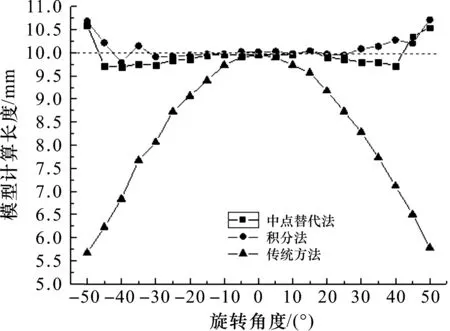
图12 擦痕的理论长度Figure 12 Theoretical length of the scratch
模拟擦痕的实际长度为10 mm,图12为擦痕在不同位置时,使用三种方法所计算出的擦痕长度,可以看出,在-45°~+45°之间时,中点替代法的相对误差较积分法略大,在±50°时,结果反而比积分法好.这是因为拟合曲线在两端出现失真,导致积分法的相对误差突然增大,所以将两端的曲线舍去,认为拟合曲线在-45°~+45°时是准确的,即圆柱工件的四分之一整圈.经计算,在适用范围内,中点替代法的平均误差为1.56%,积分法的平均误差为0.91%,传统检测方法的平均误差为14.58%.
本文以实际圆柱工件为例进行检测.首先用白纸围住工件并标记擦痕的两端,再用游标卡尺测量标记的两端点长度,取三次测量平均值,认为擦痕的实际长度为17.01 mm.在实验台上重新标定计算拟合曲线,在擦痕正对相机和擦痕在左右不同角度各取4次,共9次测量.使用积分法计算擦痕长度,其中擦痕正对相机是计算的长度为17.09 mm,其余位置的长度如表2.经计算平均相对误差为1.57%,受处理算法的不完善等影响,此结果相比实验室的理想擦痕准确度低.

表2 计算的擦痕长度

图13 实物检测Figure 13 Target detection
4 结语
针对圆柱工件表面缺陷检测时出现的曲面缺陷检测时物理尺寸不准确的问题.本文提出一种圆柱工件表面缺陷视觉检测的标定和补偿方法,通过圆柱上点像素和实际物理尺寸的对应关系曲线,在圆柱工件检测时,对不同位置的缺陷进行补偿,取得了良好效果.搭建检测系统,实验结果表明,这种方法可以抑制噪声干扰,理想条件下,理论测量结果与实际相差0.91%,提高了检测准确度,节约了时间和成本,为基于计算机视觉的光电检测提供了新的思路和方法.
