驱动桥桥壳振动模态分析及有限元优化研究

赵冰，范先虎

（陕西汉德车桥有限公司，陕西 西安 710200）

前言

模态分析在工程中应用甚广，例如对悬索桥进行模态分析，可知它在风或其它激励下是否会发生共振，并可预估寿命。在机械领域中，对零部件进行模态分析，有助于识别振动引起的故障和噪声。本文使用有限元分析手段，除了对桥壳模态进行分析，还使用有限元优化模块对零件进行了轻量化和固有频率的优化。

1 桥壳的固有模态分析

对模型进行模态分析最终是为了得到三个量：频率、振型和阻尼。但是一般情况下，仅可以得到频率和振型。结构的频率与质量及刚度有关，边界条件则影响着振型和刚度计算。因此施加不同的约束条件，会得到不同的模态振型和频率。

本文模型采用轻卡驱动桥壳，约束条件为固定桥壳两端。通过有限元分析，得到其前8阶模态分析结果，见图1、图2和表1。

图1 桥壳2阶模态

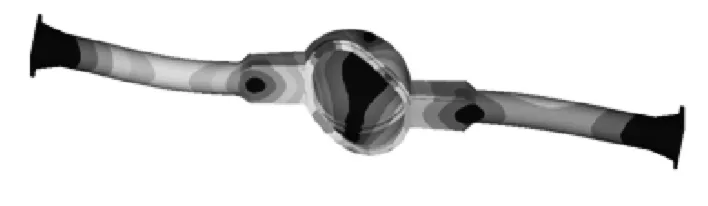
图2 桥壳8阶模态

2 桥壳结构的动力学模态分析

2.1 桥壳的频率响应分析

频响分析和模态分析类似，用于计算零件本身的特性。零件实际工作中的振动状态，需要利用试验方法、实地采集或动力学分析去计算出实际的激励频谱，然后将其加载到结构上进行计算，从而可以得出每一点的振动速度、加速度和位移信息。做频响分析的目的是看结构对于哪个频段的响应比较大，然后再与激励去对比。若存在着重合，而且响应强的频段恰恰又是激励强度大的频段，那就要通过结构改进去改善共振问题。

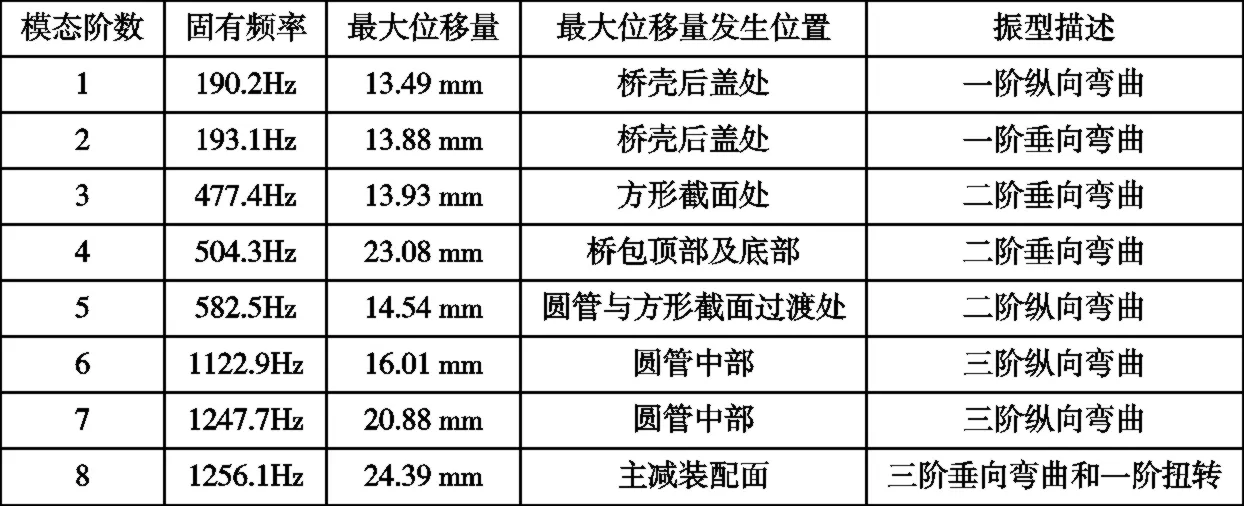
表1 桥壳各阶固有模态分析结果

本文模型，采用某实验场地的比利时路谱。其中，桥壳圆管中部某点计算结果为，X和Z方向响应较微弱，三个方向上的响应与激励的幅值变化趋势基本一致。Y方向上幅值较大。最大幅值出现在起始频率，见图3。

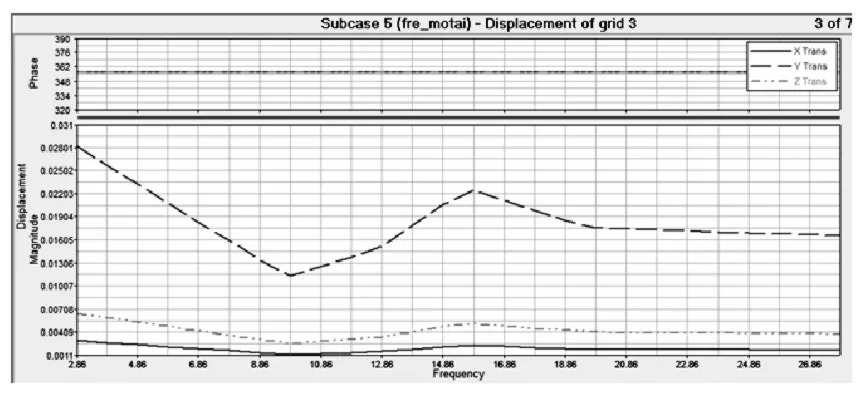
图3 比利时路况的响应结果曲线

2.2 桥壳的模态瞬态动力分析

瞬态动力学分析，用于确定承受随时间变化的承载结构的动力学响应，亦称为时间历程分析。瞬态动力学的基本运动方程是：

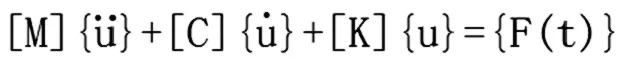
其中，［M］为质量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵，｛u｝为节点位移向量，为节点速度向量，为节点加速度向量。

在任意给定的时间内，瞬态动力学的基本运动方程可看作是一系列考虑了惯性力（方程第一项），阻尼力（方程第二项）的静力不平衡方程。

本文模型的瞬态动力响应激励采用的激励形式为：f(t)=AF(t-τ)。F是与时间相关的动载荷，振幅A的类型为力或者位移。动载荷计算方法为线性插值法。在桥壳板簧处施加轴荷。

桥壳圆管中部某点的瞬态分析曲线图，见图 4。分析结果：位移量的增幅在0.039mm左右，衰减至零时，位移量为7.81mm。

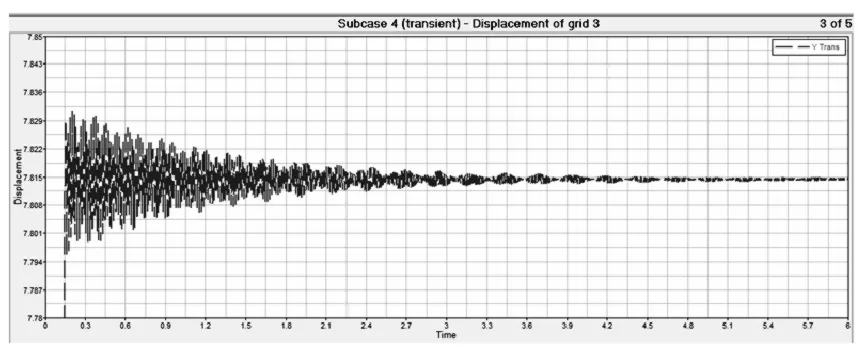
图4 瞬态响应分析曲线

3 桥壳的结构优化分析

3.1 桥壳的轻量化

本文在模型的静态工况的基础上进行轻量化，其中包括结构模型的载荷和约束。选取进行体积优化的结构作为优化目标，设置材料应力范围，结果要求设计区域的材料最少。其原理是以单元密度作为设计变量，除去低密度区的单元，从而去掉不必要的材料。设计人员需要结合实际应用，考虑结构是否需要封闭及制造工艺性，确定最终方案。本文模型一共进行了14次跌代。通过改变密度阈值，可以得到不同的等值面图，见图5和图6。

图5 密度阈值为0.3时的等值面图

图6 密度阈值为0.8时 的等值面图

3.2 桥壳的形貌优化

形貌优化用于设计薄壁结构的强化压痕，在解决轻量化问题的同时满足强度和频率等要求，可以在板形结构中找到最佳的加强肋分布。为了便于制造，可以增加合理的对称约束。由于本模型的优化区域为方形，故将生成的肋设置为直线形且采用对称约束。

优化过程进行2步迭代后结果,起肋最大高度为1.6mm。起肋效果见图7。

图7 形貌优化结果

3.3 桥壳固有频率的优化

桥壳作为承载件，地面和悬架传来的振动、传动系自身的振动都会通过桥壳相互影响。共振不利于传动系的寿命，还会引发较大的噪音。下文主要讨论通过结构优化，避免桥壳固有频率与主减速器的齿轮副的啮合频率范围的重叠。

通过理论计算，可以得到轮齿的啮合频率。啮合频率公式如下：

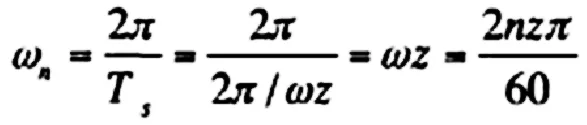
式中，n、z分别为齿轮的转速和齿数。

本文中，桥壳的第一阶固有模态频率与理论计算得到的主减速器啮合频率较为接近，目标定为提高桥壳的第一阶固有频率。计算结果见图8。

图8 提高1阶固有频率的形貌优化结果

4 结束语

桥壳作为承载件，不仅要考虑承载性能，还要考虑作为传动系的封闭腔体应注意的共振问题。