某全地形车双横臂独立悬架转向梯形断开点优化研究

赵萍，姜永晴，肖冰

（陕西重型汽车有限公司，陕西 西安 710200）

前言

悬架是现代汽车上的重要组成部分，它把车架与车轮弹性连接起来，用于传递车架和车轮之间所有的力和力矩，缓和由路面不平传递给车身的冲击载荷，保证车辆平顺行驶。悬架一般由弹性元件、导向机构和减震器组成。独立悬架由于能较好地保持车轮与路面的接触，提高离地间隙、改善通过性，被越来越多的应用于轿车、轻型客车和越野车上。不等长双横臂式独立悬架通过合理的设计摆臂参数能获得良好的综合性能。独立悬架采用断开式转向梯形，为了使悬架与转向梯形相匹配，主要工作就是确定断开点位置。对断开点位置进行合理的优化。作者以某全地形越野车不等长双横臂式独立悬架为研究对象，在ADAMS中建立转向及悬架系统虚拟样机，研究在该悬架系统下断开点位置与车轮跳动时前束角变化趋势，使车轮上下跳动时，由转向杆系与悬架运动干涉所引起的前束角变化尽可能小。

1 简化模型的建立

双横臂独立悬架的简化模型如下图1所示，以前悬架一半结构为研究对象，悬架结构由上横臂EC、下横臂GD、主销EG构成，C、D点为销轴连接（假定销轴与车辆纵向平行），E、G点为球头连接，OU为转向梯形臂、UT为转向梯形横拉杆、两端球头铰接连接、T点为断开点。当车轮上下跳动时，悬架上下摆臂分别绕C、D点转动，横拉杆UT同时绕T点转动，UT同时拉动OU，使车轮绕主销转动，产生车轮前束角α。现在悬架系统建立前提下，建立悬架系统和转向梯形的平面理论模型，利用平面作图法，初步确定断开点T位置坐标。此方法由于忽略了主销后倾角和上下摆臂摆动轴线空间角度的影响，用此方法确定的断开点位置具有一定参考性，但无法达到最优，仍有优化空间。结合ADAMS仿真软件，建立空间仿真样机，对断开点位置做进一步仿真优化。

图1 双横臂悬架理论简化模型

2 虚拟仿真样机的建立

以双横臂悬架理论简化模型为基础，在ADAMS/View中建立悬架及转向系统的仿真模型，如下图2所示。将车轮、轮轴、主销和转向梯形臂GF以固定副连接，上横臂与主销连接点B、下横臂与主销连接点C、横拉杆与转向梯形臂连接点F、断开点与摇臂连接点E均为球形副连接，上、下横臂与车身连接点A、D分别绕地面做旋转运动，轮胎支撑于试验平台上，与平台之间为点面接触，在平台上施加上下运动的移动副，模拟车轮跳动。

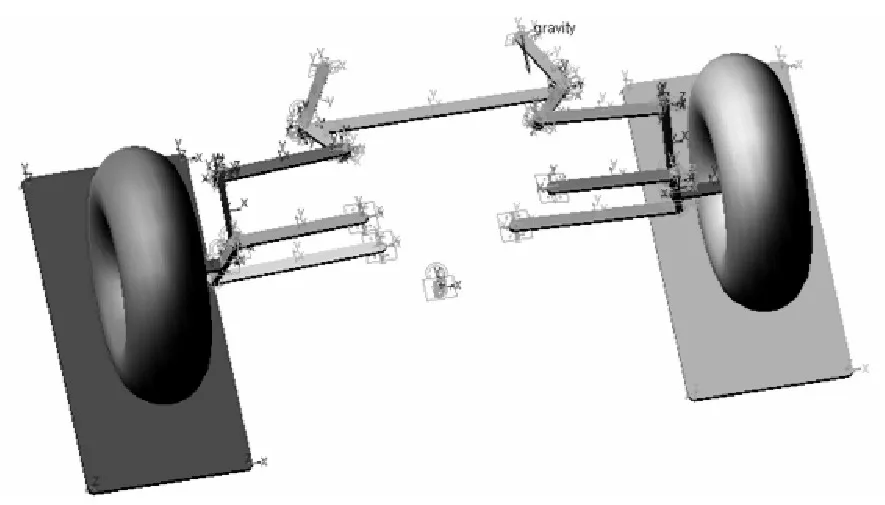
图2 虚拟样机简化模型

以某全驱车悬架及转向系统为研究对象，以平面作图法初步确定断开点坐标为（X、Y、Z），当车轮上下跳动时，得到目标函数与车轮跳动量曲线图，如下图3所示，设定向上为正。由图3目标函数仿真曲线得出，在车轮上下跳动时，优化前的车轮前束角分别为0.14°和0.42°，仍可进行进一步优化。

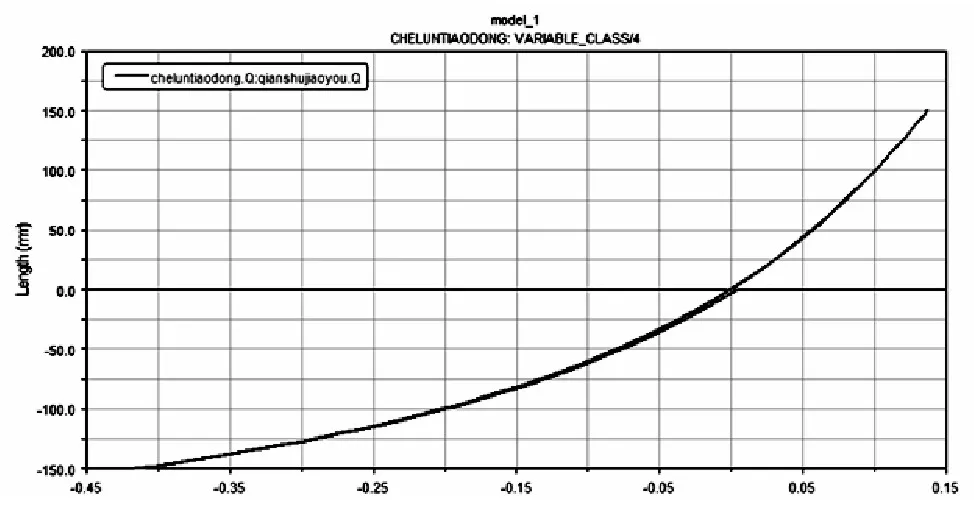
图3 目标函数变化曲线

3 优化仿真

在ADAMS/Insight中进行参数化优化分析，设置断开点坐标为变量（DV_1、DV_2、DV_3），前束角α为目标函数，优化的目标函数求最小值，考虑断开点空间位置约束，设置相应约束条件，进行仿真分析。设置断开点坐标变量变化范围，考虑到断开点基础坐标为平面作图法得到坐标，设置坐标变量变化范围为百分比相对偏差±10%，对三个设计变量设置2个水平，共进行9次矩阵模拟试验。选择目标函数的最小值为研究对象，通过不断调整变量，得到最优仿真结果。优化后的仿真结果曲线如下图4所示，由图4优化后的目标函数仿真曲线得出，当车轮上下跳动时，优化后的车轮前束角分别减小为0.09°和0.1°。

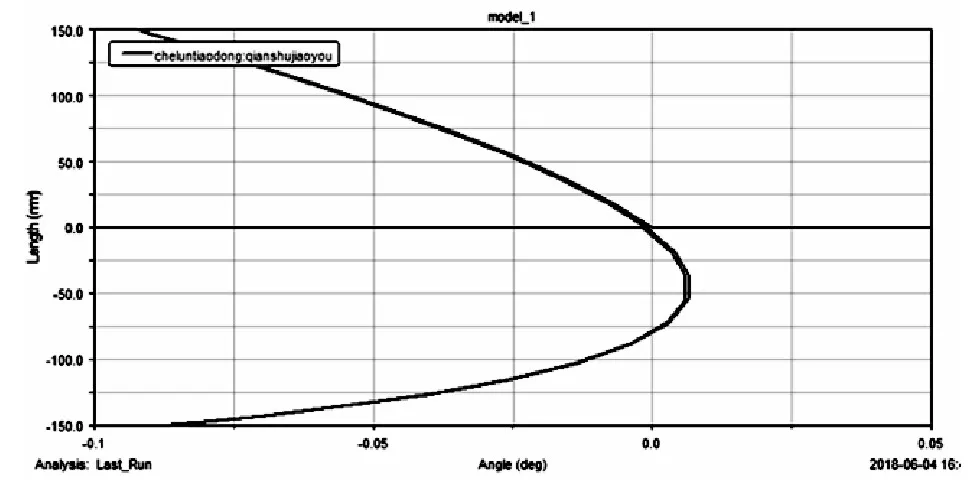
图4 优化后目标函数变化曲线

4 结果分析

通过对断开点坐标进行参数化设置，优化仿真，使车轮上跳时前轮前束角由最大值0.14°减小为0.09°，车轮下跳时前束角最大值由0.41°减小为0.1°。优化后的车轮前束角变化值控制在0.1°内，满足前束角设计要求。

5 结语

本文在以某全地形车双横臂独立悬架设计完成基础上，通过匹配设计断开式转向梯形，确定断开点位置坐标。得出了断开式梯形设计步骤，首先进行梯形设计理论分析，结合平面作图法初步确定断开点位置坐标，最后在ADAMS中建立虚拟样机，优化仿真分析。该设计方法具有一定的通用性，能很好的指导独立悬架转向梯形断开点的设计，通过该方法优化后能得到较小的理想前束角，从而能减轻轮胎的磨损及提高转向操纵的稳定性。