探究气候变化因素对国家脆弱性程度的影响

2018-10-20田萌萌

炎黄地理 2018年7期

田萌萌

摘要：当今气候变化的不稳定日益影响着人们的生活。由于气候变化引起的各种灾害也增加了国家的环境脆弱性。为了研究气候变化对FSI的影响，并确定其影响的程度，计算干预成本在某个特定区域的大小，本文通过建立基于主成分分析，干预成本模型和优化模式的BP神经网络模型来探究解决上述问题。使用主成分分析，将定量的15个气候影响因子筛选，划定为三类：暴露程度，敏感性和适应性，对FSI体系进行定义。利用澳大利亚，叙利亚和乍得2006年至2017年气候变化影响因子的因子数据对建立BP神经网络模型检验，对这些国家的国家脆弱性进行综合评估。在BP神经网络模型的基础上，通过对以上三个归类指标的回归分析，提出影响FSI的气候变化的直接和间接手段，给出解决措施。又建立干预成本模型，使用回归分析来确定项目成本与年份之间的关系，湖泊治理成本与年度之间的关系。全面考虑到鉴于较大区域的总影响是小区域整体影响的结果，却不是简单的求和过程。因此，本文通过添加权重算法，优化BP网络模型适用区域的模型区域，并绘制结果，以便运用与更大的区域范围。

关键词：国家脆弱指数；主成分分析；BP神经网络模型；干预成本模型；气候变化

1 背景

气候变化与自然生态系统和人类社会系统密切相关。气候的自然波动是地球气候系统所具有的基本特征之一，生态系统和人类社会能够适应一定范围内的气候变化。然而随着人类社会活动的增加，特别是工业革命以来人类活动工业化过程的经济活动引起的气候变化导致灾害性气候事件频发，冰川和积雪融化加速，水资源分布失衡，生物多样性受到威胁。气候变化还引起海平面上升，沿海地区遭受洪涝、风暴等自然灾害影响更为严重，小岛屿国家和沿海低洼地带甚至面临被淹没的威胁。气候变化对农、林、牧、渔等经济社会活动都会产生不利影响，加剧疾病传播，威胁社会经济发展和人民群众身体健康。

脆弱性是区域承灾体受到灾害打击时所表现出来的脆弱程度，国家脆弱性是指国家原本的正常社会运行系统的功能被扰乱，超过了该国承受的“阈值”，政府为其人民提供基本生活必需品的能力；一个不愿或不能为其人民提供基本生化必需品的国家是一个脆弱的国家。因此研究一个国家是否脆弱，采用什么方法降低其脆弱性，以及现在影响越来越明显的因素气候变化如何增加国家的脆弱性等一系列问题，可以找到某个国家是脆弱国家的原因，以及通过哪些措施减缓该国的脆弱性程度。气候变化所产生的影响具有显著的区域性差异和无法直接观测的特点，但是根据不同国家气候变化的特点制定减缓国家脆弱性的措施可以有效的预防和降低气候变化对该国的影响。因此，不论是从减缓国家脆弱性还是从预防方面，该问题的研究都有很大的意义。

2 假设

全球气候变化在未来一段时间内不会发生灾难性的变化，除了变量因素外其他因素保持稳定。一个国家经济、政治和社会价值可以被衡量。

3 定义总体主要变量

4 模型建立与分析

4.1 Model1主成分分析模型

在前期搜集的12个原始数据（Z1，Z2，Z3，…Z12）基础上，对各气候条件指标量分析筛选，最终留下3个气候指标（Z13，Z14，Z15）。故我们一共可以确定15个指标。这15个指标之间存在一定的相关性，若直接把此种一定程度上有重叠的信息直接输入神经网络进行预测，不仅会给网络运行造成负担，还可能降低神经网络的泛化能力。因而我们考虑使用主成分分析得到相对较少且线性无关的变量代替原有15个指标，达到降低维数且尽可能多的反映原有信息的目的。

利用SPSS对搜集到的15个指标相关数据进行处理，得出以下表数据结果。

由碎石图知，从第三个主成分起，变化趋势开始趋于缓慢，故可以考虑用前3个主成分反映原15个指标；由表可看出，前三个主成分的累积贡献率达到86.2%。因此，我们考虑只取前三个主成分，且它们能反映原15个指标的大部分信息。

（表2中1，2，3列下的数据分别表示3个主成分对应的特征向量，且对中间计算数值进行了省略）

综上，前三个主成分分别表示为：

Y1=0.947Z1+0.792Z2+0.835Z3+0.254Z4…+0.794Z15 （1）

Y2=-0.207Z1-0.520Z2-0.346Z3+0.859Z4…-0.295Z15 （2）

Y3=-0.058Z1+0.145Z2-0.148Z3+0.034Z4…+0.209Z15 （3）

其中，C1，C2，C3，E1，…X1表示原12个指标。

为了方便之后对主成分做实际意义的解释，对于表2中数据进行旋转变换得表3，使表中所有的数据要么偏向于0要么偏向于+1或-1.

依旋转成分矩阵得表4中三个参数的比较，将15个指标划分，将三个主成分定义为暴露程度，敏感性，适应能力。其中暴露程度理解为对国家脆弱性的直接威胁及气候变化的性质和程度（如CO2排放量，森林面积，耕地面积）；敏感性指能加重或缓解不利因素的自然-社会条件，适应能力理解为能避免潜在影响的适应能力措施。

由此得出以下神经网络结构图：

4.2 Model2 BP神经网络模型

（1）BP神经网络的算法设计图

（2）模型的变量（参数）表

（3）模型的假设条件

1）训練步骤是按照数据批量形式进行的；

2）阈值写成与权值相似的形式，阈值看做样本输入为1的随机数，下面会做具体说明；

3）原始数据给出了2006～2017 每年多个国家的相关数据。通过数据库收集的三个气候变化因子的但数据输入是按照每一行的作为一个输入维度，将15个因子的具体数据进行转置处理；

4）第一层神经元中放置的是线性函数，所以网络第一层输入和输出都等于实际输入样本的值，=X；

5）隐含层神经元激励函数为单机S型函数。

6）隐藏神经元的计算方式：

7）网络学习速率：

8）训练的目标误差：

9）M=F

（3）模型的具体步骤

1）样本的收集和准备

所研究的国家脆弱指数根据现有的指标体系，与c1，c2，c3…等十二个因素有关。根据题目要求，我们通过数据搜索决定引入氣候因素变量对于国家脆弱指数的影响。且将co2排放量，森林面积，耕地面积作为参与模型建立的气候因素。这十五个因子便是网络输入样本，”国家脆弱指数”便是网络训练的输出样本.从而建立了15输入1输出的BP网络模型。国家脆弱指数作为衡量一个政权或者政府为其人民提供生活必需品的能力和意愿能力对于社会稳定环境和国家治理以及其他诸多方面有着重要关系，因此成为当今越来越受重视的一个指数。

2）确定网络的初始参数

网络训练的参数根据实际拟合效果进行自主选择。样本输入采取批量输入，因此选用matlab进行for循环运算，可求的符合要求的动态拟合图形。根据假设条件可知。

3）初始化网络权值和阈值

初始化网络即给网络的权值和阈值赋予随机数矩阵。因为是15个输入因子14个隐含层神经元，则第一层与第二层之间的权值为14*15的随机数。

神经网络的阈值是指用来激活神经元而设置的一个临界值。根据神经网络的结构可知第二层神经元的阈值为14*1的矩阵。

同理，第二层与第三层之间的权值为1*14的随机数矩阵；

同理，第三层阈值

4）计算第一层神经元的输入和输出

设X为输入样本，则输入规模为15*12的矩阵。此处需要对输入和输出样本做归一化处理以便达到相同量级。是一个15*12的矩阵。

5）计算第二层神经元的输入

对于第二层，神经元的输入一定来自第一层所有神经元的值与阈值的和，即，是一个14*12的矩阵，其中ones是一个全为1的矩阵。

6）计算第二层神经元的输出

假设隐含层神经元激励函数为单机S型函数，即为

所以二层神经元的输出：

同时第二层输出也是一个14*12的数据矩阵

7）计算第三层的输入和输出

第三层即输出层与第二层类似，，是一个1*12的矩阵

对于国家脆弱指数的分层为三层，输出数据之后结束。

8）计算能量函数E

计算能量函数（网络输出与实际样本之间的误差平方和）的目的是达到预定误差就可停止训练网络。假设实际输出样本为Y，

9）计算第二层与第三层之间权值与阈值调整量

这是一个链式偏微分：

因此，是一个1*14的矩阵

同理，

可知，是一个1*1矩阵

10）计算第一层和第二层隐藏层之间权值和阈值调整量

计算第二层和第三层之间的权值和阈值调整量，而后才计算第一层与第二层之间权值和阈值调整量，得出误差反向。

对于激励函数

求导的特征：

从而得到：

因此，是一个14*15的矩阵：

同理，

为14*1的矩阵

11）计算调整后的权值和阈值

把t时刻的各层权值和阈值加上各自的调整量赋予t+1时刻的权值和阈值：

12）网络输出的值得还原

之前初始化数据对输入和输出样本进行了归一化处理，最后需将还原成原始数据的量级。

是一个1*14的矩阵。

（4）模型结果图示

下面根据2006～201715个因子数据为输入样本，2006～2017叙利亚的FSI为输出样本进行网络训练动态拟合，选出相对精确地拟合求的结果。

在加入气候指标的条件下，我们重新定义国家脆弱性指数，并将它划分为极度脆弱、中度脆弱、轻度脆弱、稳定，划分标准如下：将苏丹和瑞士两个国家的三级指标代入模型，得到两个国家在含有气候影响下的脆弱性指数，分别为27.4，123.1，所以粗略划定范围是（27.4，123.1），由于两个数据具有特殊性，故应适当扩大该区间，得到（20，140），将其等间距划分为四等份，国家脆弱性指数小于第一分割点值的国家定义为稳定型国家，介于第一分割点值和第二分割点值的定义为轻度脆弱国家，介于第二分割点值到第三分割点值的定义为中度脆弱国家，大于第三分割点值的定义为极度脆弱国家，如下图

计算各分割点值的公式：

得范围为（20，50），（50，80），（80，110），（110，140）

4.3Model 3 回归模型（分析）

对于各国家，通过对气候指标与国家脆弱指数，气候指标与除气候指标外12个指标进行回归分析，利用R2值解释气候变化通过哪个气候指标直接或间接增加了国家脆弱性。

利用BP神经网络模型和MATLAB软件，可得到加入气候变化条件下国家脆弱性指数随年份的变化曲线，即有气候条件下国家脆弱性指数的具体值已知了。我们可以选取某个国家为研究对象，分别对3个气候变化指标CO2排放量，耕地面积，森林面积与该国家脆弱性指数间进行回归分析，分别得到CO2排放量，耕地面积，森林面积与该国家脆弱性指数的相关系数，比较这三个相关系数值，最大R2值对应的那个指标体现出它与国家脆弱性指数的关系很大，能直接影响国家脆弱性指数，因而气候变化就是通过该R2最大值对应的指标直接影响了国家脆弱性。

下面考虑间接影响，再次运用回归分析求出3个气候变化指标与其他12个指标的相关系数，根据R2值大小判断各气候指标与其它12个指标间关系的强弱，R2值越大，说明该气候指标与另一指标间关系越强，因而气候指标可通过先影响该相互关系较强的指标进一步影响国家脆弱性。

（注：以下结果分析中若R2>0.5，我们认为两者由相关关系，且R2越大，关系越强）

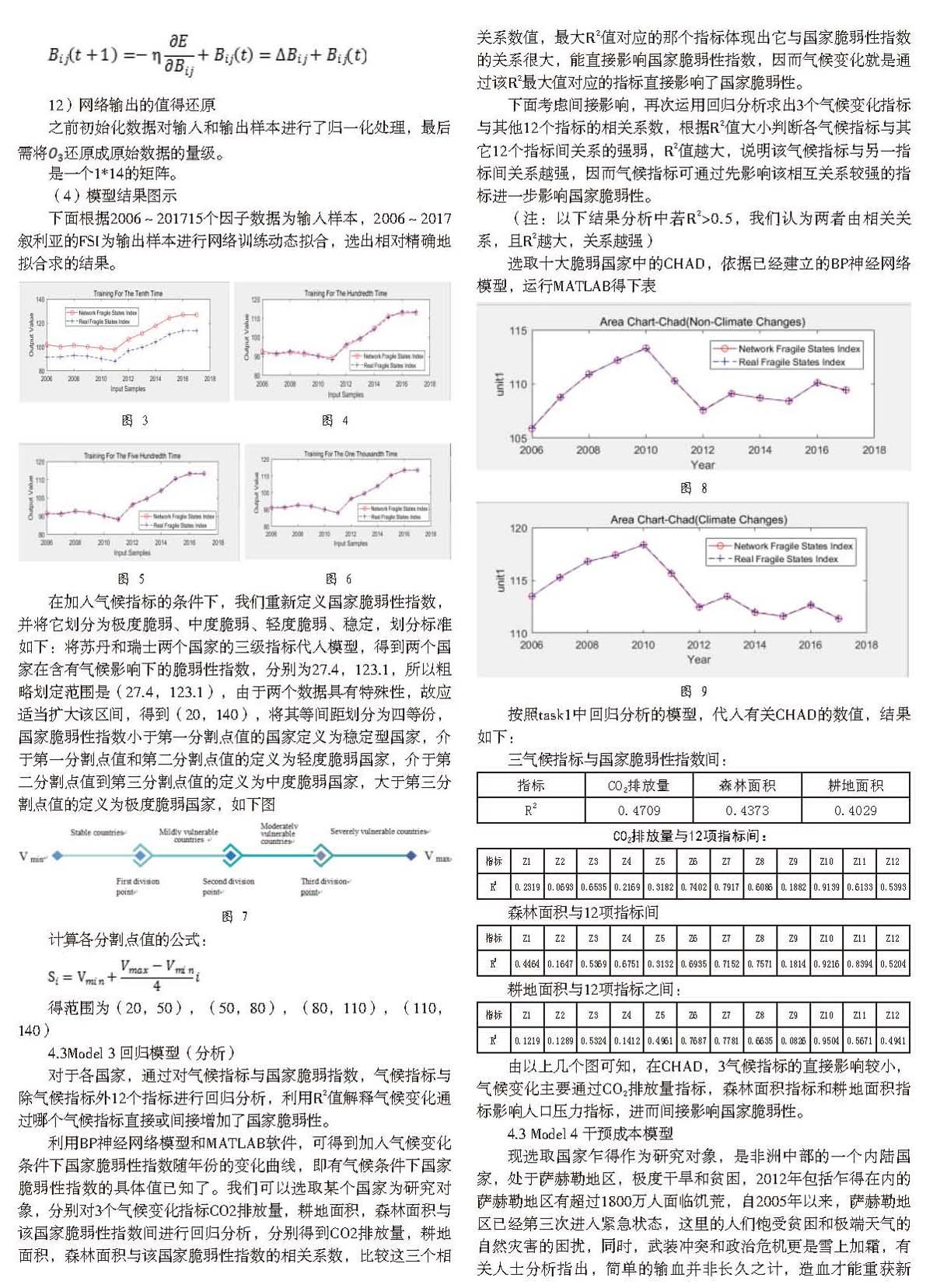
选取十大脆弱国家中的CHAD，依据已经建立的BP神经网络模型，运行MATLAB得下表

按照task1中回归分析的模型，代入有关CHAD的数值，结果如下：

三气候指标与国家脆弱性指数间：

由以上几个图可知，在CHAD，3气候指标的直接影响较小，气候变化主要通过CO2排放量指标，森林面积指标和耕地面积指标影响人口压力指标，进而间接影响国家脆弱性。

4.3 Model 4 干预成本模型

现选取国家乍得作为研究对象，是非洲中部的一个内陆国家，处于萨赫勒地区，极度干旱和贫困，2012年包括乍得在内的萨赫勒地区有超过1800万人面临饥荒，自2005年以来，萨赫勒地区已经第三次进入紧急状态，这里的人们饱受贫困和极端天气的自然灾害的困扰，同时，武装冲突和政治危机更是雪上加霜，有关人士分析指出，简单的输血并非长久之计，造血才能重获新生，因此，要提高乍得的灾害风险管理能力，减轻气候变化的风险，防止乍得的脆弱指数进一步提高，并解释人类干预的成本，建立一个干预成本模型，再从植被种植与防治乍得湖面积减小的成本分析。

4.3.1假设

①不考虑土壤及地形的影响，即国家内部的所有研究的地质是均匀的，换句话说，树苗在该国的任何地区的存活率是相同的；②当国家森林覆盖率由如今的9.3%到20%，便可以认为该国家以达到其干涉预期；③由于湖泊治理是长期的方案，所以可以近似认为在森林覆盖率到达期望值时，湖泊治理的成本并没有改变很大，因此可以用该国人均GDP的5%来表示湖泊治理。

4.3.2研究方法：

植树的成本主要有人工成本，树苗成本，管理费这三个成本子项目，现在，拟分析树的种植的三个成本子项目对总成本是否会产生显著影响，显然，该问题是两个以上自变量对一个因变量的数量变化关系，因此，采用多元线性回归模型进行分析：

Y=β1x1+β2x2+β3x3+ε （1）

其中：y为因变量，即植树的总成本；x1，x2，x3为自变量，即植树的三个成本子项目；

β1，β2，β3是自变量系数，ε是误差项。

4.3.2树苗种植成本增长分析

查找近四年来植树成本增长表如表1所示，年增长率增加5%，人工成本和管理费分别增长4.1%和3.6%，可知，植树成本的增长主要是受人工成本与管理费这两个成本子项目的影响，这位降低成本提供了参考方向。

4.3.3植树成本模型构建

由于三个成本子项目的相关性很小，所以总成本就可以近似成三者的加和，根据假设，当植被覆盖面积到达20%时，可以认为在植被方面已经达到了指标，为减小误差，接下来用一元线性回归找到人工成本，树苗成本，管理费这三项分别与时间的关系：

人工成本：y1=19.975x^2-80470x+8E+07；

树苗成本：y2=-37.267x^3+225321x^2-5E+08x+3E+11；（2）

管理费： y3=-28.8x^3+174147x^2-4E+08x+2E+11；

所以，植树成本是Y1=y1+y2+y3

4.3.4 以乍得为例

乍得湖是非洲第四大湖，由于干旱等自然现象和大规模灌溉等人为因素的影响，使得乍得湖面积急剧减少，而乍得湖面积的减少又加重了干旱的程度，使农业灌溉的水竞争力又加大，从而形成恶性循环，并且由于农业灌溉在一定的时间内不会有太大的变化，因此可以假设乍得湖的治理成本用该国人均GDP的5%表示，即：

Y2=5%*GDP （4）

即：Y2=0.0785x^5-75.795x^4+6E+0.6X^3-1E+10X^2+1E+13x-5E+15

最终，干预成本W可以表示为：

W=Y1+Y2 （5）

比如，2018年的人均GDP为600，求出的干预成本为5672.18元。

5 模型扩展

对于小区域，比如一个城市的脆弱指數，可通过查阅文献找到该城市的各三级指标（即影响城市脆弱指数的影响因子）和脆弱性指数，在用BP神经网络模型利用MATLAB软件，将实际脆弱性与网络输出的脆弱性比较，结果发现相关的值都与实际指标相符合。可以说明我们建立的模型可应使用于较小的区域。

对于大区域，比如一个州，全世界，是无法直接根据已建立的模型求解。模型不适用于较大地区主要是因为较大地区的各项三级指标是根据组成各大地区的各部分的三级指标给出的，各部分的各项指标是已知的，但是由于内在因素的影响，比如地形，地貌，战争，气候等等，区域小的这些因素可直接得出带入模型，但是区域大时需要考虑各部分某一因素对整个区域的该因素的权重，进而间接求出大区域的各项指标。

因此可利用多元回归等模型先得出各项指标模型，在带入数值求的结果，将结果作为已建立的BP网路模型就可以得出结果。这便是对我们模型的一个完善和修改。

假设：在大区域的适应能力方面，其权重根据各小部分（如国家）在大区域内的地位（可以根据国家GDP来排名）来表示，级地位越高，其适应能力越强，其脆弱性越小，假设Dij

（j=1，2…n，i=1，2…n）代表第i小区域的第j个反映适应能力的三级指标，Dj代表大区域的第j个反应适应能力的三级指标，Pij（i=1，2，3…，j=1，2，3）代表第i个小区域第j个三级指标在大区域内的排名，该大区域可以分成N个小区域，可以根据排名来计算权重Eij：

所以能求出大区域的个三级指标：

这样，大区域的各三级指标可以求出来，再代入原有的模型就可以求出大区域的脆弱性。

6 模型评价

我们基于衡量国家的脆弱性的模型，其衡量标准是很容易计算的，并且在计算国家脆弱性时几乎涵盖了所考虑的所有的指标，而且计算国家脆弱性所需要的在国际组织的数据库中也有，因此，它可以很容易地用于计算大多数国家脆弱性指数；在考虑各气候指标对国家脆弱性直接和间接影响时，用回归分析该法简单直接地找到它们之间的关系，用较为简单的方法解决了问题；干涉成本模型中，直接找到了年份与成本的关系式，直接代入年份就可以算出成本，思路简单可信；BP神经网络模型突出优点就是具有很强的非线性映射能力和柔性的网络结构，结合本体，可较为简单的得出结论。但由于找到的数据有限，本文仅对找到数据的指标进行了主成分分析，因此存在对国家脆弱性指数有影响的气候指数但没有考虑的情况；模型简单虽然是该论文的一大优点，但是同样会有精度不够高，不全面的缺点，但是方法的可行性不可否认；干预成本模型中得到的年份与成本的关系太过复杂，对计算的要求很高，而且以现有知识无法明确的找到治理湖泊成本与人均GDP的关系。

参考文献

[1] 刘毅，黄建毅，马丽.基于DEA模型的我国自然灾害区域脆弱性评价[J].地理研究，2010，29（7）：1153-1160

[2] 温宁，刘铁民.基于对抗交叉评价模型的中国自然灾害区域脆弱性评价[J].中国安全生产科学技术，2010，7（4）：24-28

[3] 杨菲，贾姗姗.区域社会系统脆弱性评价[J].国家科学社会基金项目，2014，3（4）：13-16

[4] 何斌，赵菲菲，李小涵，王前锋.区域农业干旱脆弱性评价及影响因素识别[J].北京师范大学学报（自然科学版），2012，48（3）：282-286

[5] 权轶，张勇传.组合预测方法中的权重算法及应用[J].科技创业月刊，2006，（5）.

[6] 马咏真，吴卢荣.中国火灾最佳灰色回归组合预测模型[J].中国安全科学学报，2006，16（1）

[7] 周慧，王晓光.基于BP神经网络的中国火灾灰色回归组合预测模型[J].统计与决策，2008（14）：39-41

[8] 张志涌，杨祖樱.MATLAB教程[M].北京市海淀区学院路37号：北京航空航天大学出版社，2015.1-100

[9] 刘浩，韩晶.MATLAB R2016a 完全自学一本通[M].北京市海淀区9万寿路：电子工业出版社，2016.1-289

[10] 卓金武.MATLAB在数学建模中的应用[M].北京市海淀区学院路37号：北京航空航天大学出版社，2014.1-241

[11] 谢金星.数学模型[M].北京市西城区德外大街4号：北京鑫海金澳胶印有限公司，2011.1-213