基于SVDI的变工况旋转机械故障诊断方法

宋 涛，王瑜琳，赵明富，钟年丙

(1.光纤传感与光电检测重庆市重点实验室，重庆 400054; 2.重庆理工大学 电气与电子工程学院，重庆 400054; 3.重庆公共运输职业学院重庆 402247)

振动信号因其信息丰富，能很好的反映旋转机械设备的运行状态而成为旋转机械设备故障诊断中最常用的信号源[1-2]。基于振动信号的智能故障诊断其一般模式为：构建故障样本库-实测振动信号-特征提取-模式识别。该模式需要收集不同故障的信号作为样本，然后通过特征提取、模式识别判断待测信号的故障类别。如果机械设备工作在平稳工况下(即恒速恒载)，该方法比较可行，已取得广泛应用，并有较好的故障识别效果[3-5]。但在一些旋转机械设备实际的工作中，非平稳工况不仅非常常见[6-7]，且具有比平稳工况更强的破坏性，更容易产生故障。由于振动信号在不同工况下的特征不一致，上述故障识别模式存在较大的局限性，变工况下的故障识别存在极大困难。

针对变工况的旋转机械设备，有学者提出基于静电监测方法对变工况下的滚动轴承进行故障诊断[8]，但该方法传感器复杂，安装困难，成本较高。更多学者基于振动信号时频分析研究变工况旋转机械故障诊断方法，以降低振动信号特征与速度工况的关联性。如希尔伯特变换[9-10]、阶比跟踪[11-12]、Kalman滤波[13]等。但这一类分析方法一方面计算相当复杂、比较耗时，另一方面更多依据经验进行人工分析，难以实现自动特征提取和后续的模式识别。另一种思路是构建完备样本库，即收集所有工况下的各种故障信号，故障诊断时根据实际运行工况选择相应工况下的信号作为样本进行模式识别。而事实上，该模式实现难度和代价非常大，因为工况通常是在一定范围内连续任意变化的，很难构建完备样本库。

针对变工况下故障诊断存在的上述难题，本文提出一种基于奇异值分解插值(Singular Value Decomposition Interpolation,SVDI)算法[14]的变工况下旋转机械设备故障诊断方法。该方法的思路为：在旋转机械设备运行工况的范围内，采集多种离散工况下的故障信号构建非完备样本库。故障诊断过程中，根据实际运行工况，利用样本库中与实际工况最接近的前后多种(四种)离散工况下的信号作为原始样本，对其进行特征提取，并采用SVDI方法对其进行拟合插值，估计出实际工况下故障特征值作为故障诊断的训练样本，再采用模式识别方法进行故障诊断。变转速下齿轮箱故障诊断的实例表明该方法的有效性。

1 SVDI算法原理

X(γ)=[x1(γ)x2(γ)…xj(γ)…xn(γ)]

(1)

xj(γ)∈Rm×1表示工况α(γ)下某种故障的第j组特征向量。如果能在工况范围内获得任意工况下的样本数据，即构建完备样本库，将能获得很高的识别精度。但实际上，运行过程中的转速和负载可能是工况范围内任意变化的连续值，无法获得所有工况的样本数据，但可以获得多种工况下的样本数据。假设获得样本的运行工况集合为

Γ={γ1,γ2,…,γl},γ1<γ2<…<γl

(2)

所有这些特征矩阵构成特征矩阵集合表示为

Z={Xγ1,Xγ2,…,Xγl}

(3)

(4)

用Xγ的协方差矩阵Cγ描述特征矩阵Xγ的形状和方向，Cγ如式(5)所示

(5)

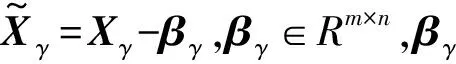
(6)

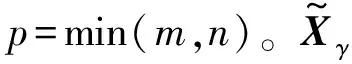
σγ，1≥σγ,2≥…≥σγ,r

σγ,r+1=σγ,r+2=…=σγ,p=0

(7)

将式(6)代入式(5)得

(8)

该式为协方差矩阵Cγ的奇异值分解。由式(8)可以看出如果已知Uγ、Σγ和n，那么Cγ可计算出来。协方差矩阵Cγ表示点云Xγ的形状和方向，进一步可以看出左奇异矩阵Uγ代表了特征空间Xγ的方向，Σγ控制Xγ的尺寸。

(1)基于样条法的均值插值

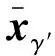
(-2t3+3t2)xγk+1+(t3-t2)ρk+1

(9)

(10)

ρk是用于决定样条方向的切向量，ρk有多种定义方式，最常用的定义方式是基数样条，定义如下

(11)

其中c是张力参数，用于控制切向量的长度，如果c=0，ρk则退化为Catmull-Rom样条

(12)

(2)Uγ和Vγ估计

(13)

其中t∈(0,1)，

(14)

(15)

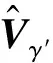
(16)

(17)

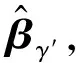
(18)

2 基于奇异值分解插值算法的变速工况下故障诊断流程

基于SVDI算法的旋转机械设备变速工况故障诊断方法流程如图1和图2所示(此处以变转速为例)。

具体步骤如下。

图1 样本库构建Fig.1 Sample library construction

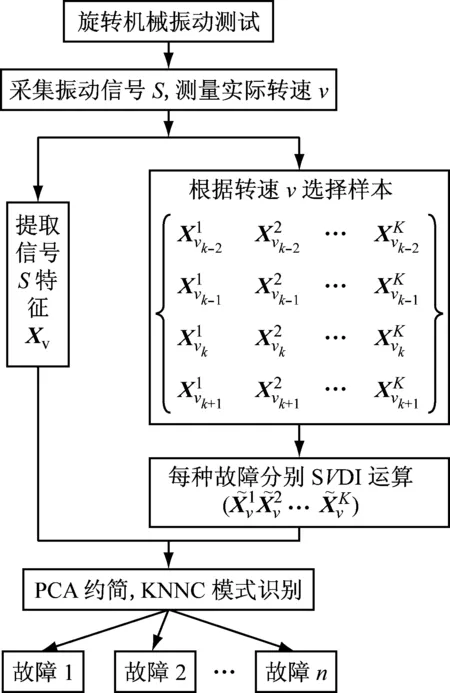
图2 基于奇异值分解插值算法的变速工况下故障诊断流程Fig.2 Fault diagnosis process under variable condition based on SVDI algorithm

步骤2 实测旋转机械设备振动信号S，并测量其转速v，提取信号S的振动特征Xv。如果v∈Γ，即样本库中有对应工况的样本信号，无需进行SVDI运算，此文不赘述。

3 变速情况下的旋转机械故障诊断应用

应用美国预测与健康管理协会提供的多种速度工况下齿轮箱故障振动数据进行故障诊断测试。该测试中所用齿轮箱结构如图3所示。图中32T、96T、48T、80T分别为输入轴齿轮、中间轴齿轮1、中间轴齿轮2、输出轴齿轮，IS、ID、OS分别指输入轴、中间轴、输出轴。

齿轮箱由输入端至输出端经过两级减速，在齿轮箱输入轴和输出轴分别安装一个振动加速度传感器同步采集振动加速度信号，型号为Endevco(10 mv/g)，同时安装一个转速计采集转速信号，分辨率为10脉冲/转。三个传感器的采样频率均为66 666.67 Hz (200 kHz/3)。

图3 齿轮箱结构图Fig.3 The structure of gearbox

该齿轮箱共采集了8种状态下的数据，包括正常状态和7种故障状态，每种故障可能是单一零部件故障或者复合故障。本实验取其中五种正常/故障状态进行测试，五种状态下各零部件对应的正常/故障状态如表1所示。表中IS:IS、ID:IS、OS:IS分别表示输入轴、中间轴和输出轴的输入端轴承。

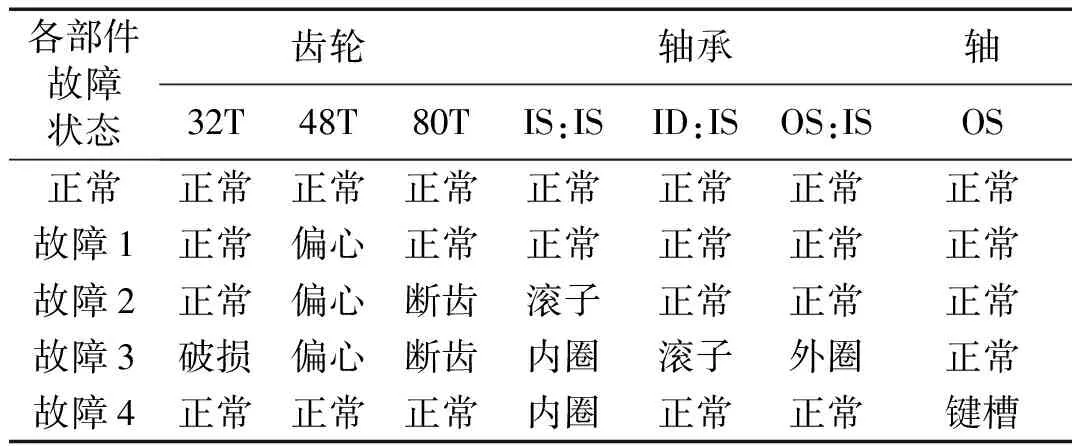
表1 齿轮箱故障状态Tab.1 The fault status of gearbox

该试验台每种故障数据分别在5种不同的转速下采集获得，分别为输入轴转速1 800 r/min(30 Hz)、2 100 r/min(35 Hz)、2 400 r/min(40 Hz)、2 700 r/min(45 Hz)、3 000 r/min(50 Hz)。本实验以输入轴30 Hz、35 Hz、45 Hz、50 Hz四种转速下的振动数据作为训练样本，以输入轴转速40 Hz的数据作为测试样本。上述5种速度工况下的故障1对应的振动信号时域波形如图4所示。

图4 五种速度工况下的故障1对应的振动信号时域波形Fig.4 The vibration signal waveform of fault 1 under five speed conditions

将30 Hz、35 Hz、45 Hz、50 Hz四种转速下每种正常/故障状态的振动数据各取50组作为训练样本，样本长度为4 096点，每组数据分别提取时域、频域特征，见文献[15]。将40 Hz转速下的每种状态的振动数据各取50组作为测试样本，长度为4 096点。并提取其时域、频域特征。样本的构建和样本数如表2所示。

显然训练样本中不包含测试样本所属的工况，因此，这里采样SVDI算法，利用30 Hz、35 Hz、45 Hz、50 Hz四种转速下的样本特征估计出40 Hz转速下的样本特征。

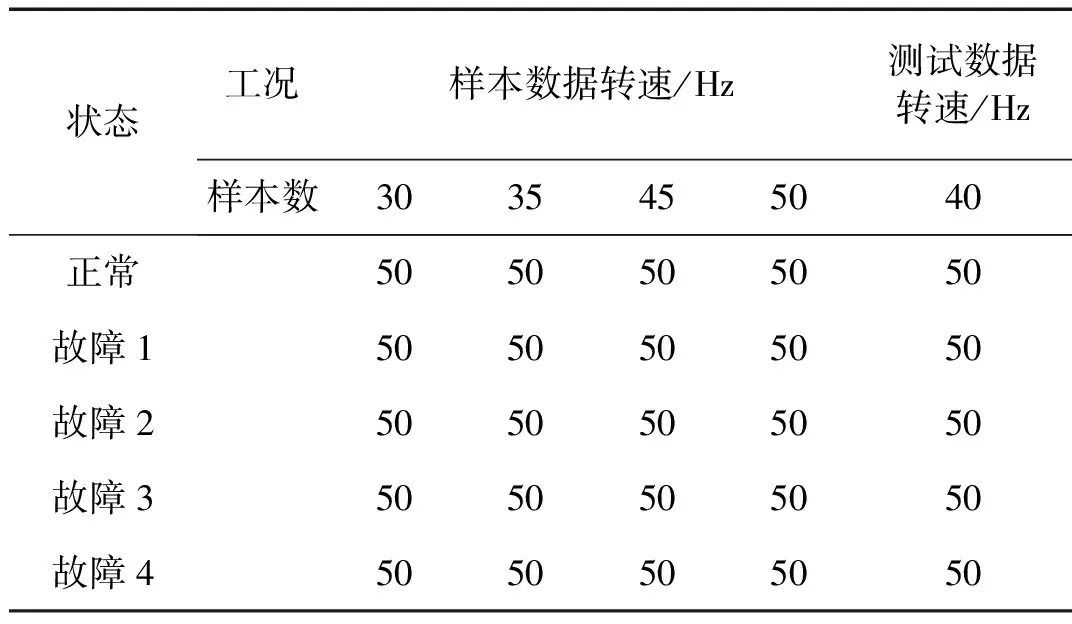
表2 样本构建表Tab.2 Sample construction table

以该估计值作为训练样本，并采用PCA方法将时频域特征23维高维特征值降低至8维，降维后的特征分布如图5所示(取其前三维绘制)，可以看出测试样本特征在空间分布上与相应正常/故障状态下的训练样本非常接近，反而，如果训练样本和测试样本不一致，其特征值在空间分布上将呈现分离现象。

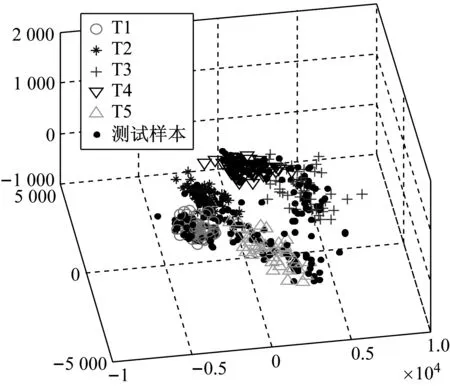
图5 样本特征空间分布图Fig.5 The space distribution of sample characteristics

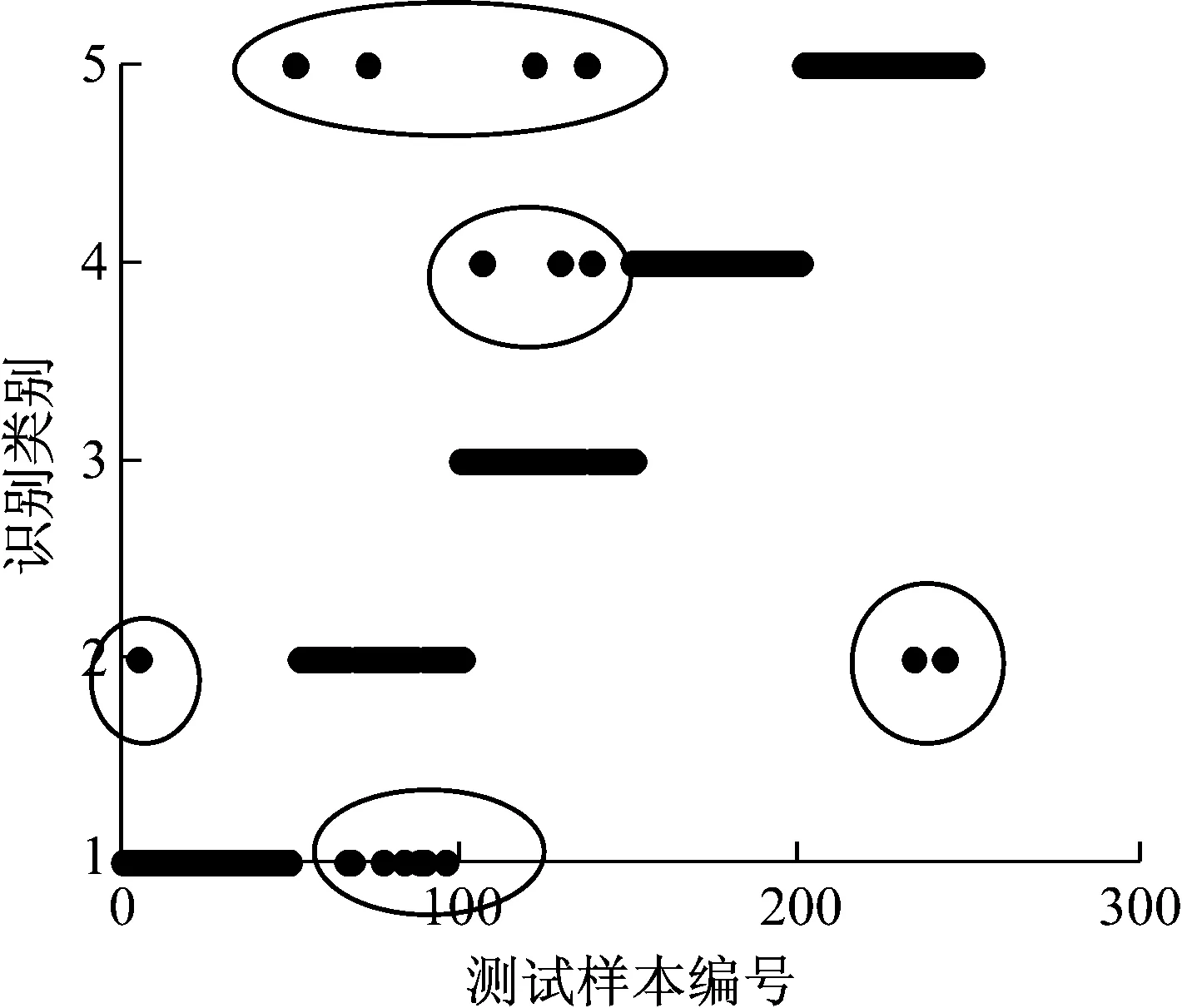
图6 测试样本模式识别输出Fig.6 The pattern recognition output of test samples

最后采用简单实用的k-近邻分类器对测试样本进行分类，近邻分类器邻域大小设置为20，五种正常/故障状态的分类输出分别设置为：正常->1、故障1->2、故障2->3、故障3->4、故障4->5，五种正常/故障状态共250组测试样本的输出如图5所示，其中圆圈标注的是误识别样本，共计18组样本识别错误，识别率高达92.8%。

为了对本方法进行比较，实验中取30 Hz、35 Hz、40 Hz、45 Hz、50 Hz五种转速下的振动数据分别作为训练样本，并以40 Hz转速下的振动数据作为测试样本，每种状态识别率以及本文方法的识别率如表3所示。可以看出，如果样本库中有对应工况的样本，则识别率最高，这种情况通常在变工况运行的设备中难以满足。如果样本库中没有对应工况的样本，而选择其它工况的数据作为样本，识别率将急剧降低，工况差异越大，识别率越低。而采用文本的SVDI方法，估计出对应工况的特征样本，将有效提高故障诊断识别率。

表3 故障诊断结果对比Tab.3 Comparison of fault diagnosis results

4 结 论

变速运行下的旋转机械设备由于无法获取完备样本库而导致故障诊断困难，奇异值分解插值算法只需采集多种离散工作下的信号构建不完备样本库，利用离散工况下的样本数据提取特征矩阵，并将特征矩阵分解为能代表特征矩阵空间位置、形状和方向的均值向量、奇异值、左右奇异矩阵，再利用插值算法估算出待测工况下的均值向量、奇异值矩阵、左右奇异矩阵，并重构待测工况下的特征矩阵作为训练样本，最后对同工况下的训练样本和测试样本采用模式识别算法进行故障诊断。该算法针对旋转机械设备运行工况范围内的任意时变工况都能有效地对其进行故障诊断。多种转速工况下的齿轮箱故障诊断实例表明了该方法的有效性。