基于自适应频带冲击强度的滚动轴承故障量化评估

张 龙，成俊良，李兴林，杨世锡

(1.浙江大学 机械工程学院，杭州 330027；2.华东交通大学 机电与车辆工程学院，南昌 330013；3.杭州轴承试验研究中心 博士后工作站，杭州 310022 )

准确可靠地告知设备维护人员何时进行何种维修是设备管理的最终目标，而故障定性和定量诊断是其技术基础。故障定性诊断即通常所谓的故障诊断，旨在故障发生后识别其性质和发生部位[1]，目的是科学指导维修过程，告诉维修人员“如何做”。而近年来渐受关注的预诊断技术(Prognositcs)则侧重研究设备剩余有效寿命预知问题[2-5]，试图告诉维修人员“何时做”。

故障量化评估是预诊断和维修决策的基础，准确评估设备当前故障劣化程度或者说性能退化程度是进行有效剩余寿命预测的前提。故障量化评估常用方法包括简单参数法和基于特征提取的相似度评估算法等。简单参数法通常直接从动态信号中提取单一参数来刻画故障劣化程度，包括峭度(Kurtosis)、歪度(Skewness) 及均方根值(RMS)等。Caesarendra等[6]以峭度作为故障程度量化评估指标，利用逻辑回归和相关向量机进行故障劣化趋势预测。Honarvar等[7-8]利用幅值校正后的振动信号的歪度检测轴承故障，实验结果表明该指标相比峭度而言对干扰性冲击不敏感、对载荷和转速变化的鲁棒性更强。RMS因能有效反映动态信号的强度，在实际中应用更为广泛。Wang等[9-10]在研究轴承预诊断问题时以振动信号通频带RMS描述滚动轴承故障程度。李力等[11]将RMS与转速之比和连续小波能量熵进行加权融合，得到一个轴承故障定量诊断指标。王红军等[12]利用速度信号通频带RMS(烈度)和特征频率幅值作为故障劣化程度敏感因子，利用支持向量机对设备劣化趋势进行预测。

考虑到各种信号处理方法和智能算法在故障模式识别中取得的良好效果，一些基于特征提取和相似度评估的故障程度评价方法相继被提出。这些方法首先对无故障阶段的信号进行特征提取并建立基准模型，最后通过评价测试样本与基准模型之间的几何距离或概率依存度来评价测试样本与无故障状态之间的相似性，从而定量评估故障程度。如Pan等[13]利用小波包节点能量方法提取轴承振动信号特征，利用支持向量数据描述(Support Vector Data Description,SVDD)建立包围无故障轴承特征空间的超球体，以测试信号特征向量到该超球体的距离作为轴承健康指标。Shen等[14]基于模糊SVDD空间距离和设备运行时间，研究了具有单调性质的故障程度指标并利用滚动轴承加速疲劳试验数据验证了方法的有效性。Yu[15]利用非线性流型方法进行特征降维并建立无故障样本高斯混合模型 (Gaussian Mixed Models,GMM)，将测试样本属于该GMM的概率作为轴承健康评估指标。

基于特征提取和相似度评估的方法期望通过合适的信号处理方法进行深层次信息挖掘，以提高故障程度评估的敏感性、一致性和鲁棒性等。然而实际应用中尚存在一些问题：① 计算量大,需要进行信号处理、特征提取、基准模型模型建立以及相似度评估；② 计算复杂,SVDD、GMM以及隐马尔科夫模型(Hidden Markov Models,HMM)[16]等的训练和测试过程复杂；③ 需要训练数据,需要无故障阶段数据建立基准模型，若设备在获取训练数据过程中发生突发故障则无法及时预报；④ 过早饱和,当GMM和HMM等概率型方法表明测试样本与无故障基准模型之间相似度为零时，设备可能并未完全进入真正的失效状态，即存在模型极限值早于真实物理失效的情况。上述不足导致基于特征提取和相似度评估的方法在工程实际应用，特别是便携式巡检仪器实现上存在困难。

事实上，工程实际中评价机器运行状态时应用最为广泛的仍然是时域统计指标如RMS等[17]，这些指标具有无需信号域变换、信息损失小、计算过程简单以及计算量小等优点。其缺点主要是与真实故障程度之间的敏感性和一致性不足等，如RMS与故障发展之间的一致性较好，但对早期故障不够敏感；Kurtosis能及时发现早期故障，但与故障发展趋势之间的相关性较差。要解决上述问题，应先了解故障轴承振动特性。当滚动轴承发生裂纹、点蚀、剥落和压痕等局部故障时，运行过程中损伤点会撞击与其接触的其它原件表面，从而产生冲击力并激励轴承系统共振。共振解调通过对局部故障冲击引起的共振频带进行带通滤波去除干扰，并通过包络解调判断有无故障和故障发生部位。大部分研究中评估故障严重程度时用到的RMS通常是指包括噪声在内的通频带即所有信号成分的有效值，因此并不能纯粹地反映故障冲击强弱。基于此，Li等[18]将3 000～5 000 Hz频率范围的RMS作为滚动轴承故障量化指标。然而被激励的轴承系统共振频率会随故障形式、位置和故障程度而改变[19]，因此最合理的方式应是针对具体信号自适应选择最优带通滤波频带。

自适应带通滤波能够去除大部分的噪声干扰信号，但对通带内的噪声却无能为力，因此带通滤波信号的RMS反映了冲击信号和噪声成分总体强度。包络谱谱峰因子(Crest of Envelope Spectrum,EC)是作者提出的反映信号中冲击成分强弱的指标[20]。本文将带通滤波信号的RMS与其EC值的乘积作为滚动轴承冲击类故障量化评估指标，反映带通滤波信号中冲击成分的强度，为故障定量评估提供一种早期故障敏感、一致性好且计算简单的方法。论文介绍了方法的理论背景，并通过人工植入故障实验和疲劳试验数据分析验证方法的有效性和优越性。

1 自适应频带冲击强度

1.1 复平移Morlet小波滤波器

Morlet复小波定义为高斯函数与复指数函数之积，其时域和频域表达分别如式(1)和(2)所示

(1)

(2)

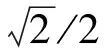
(3)

可知Morlet小波等效于一个通带为[f0-β/2,f0+β/2]的带通滤波器。用带宽参数β代替式(2)中的σ，Morlet小波的频域表达式可以写为

(4)

通过选择不同带宽β并对中心频率f0进行平移可得到不同的滤波器，同时因为Morlet小波的时域为复函数，所以这种小波滤波被称为复平移小波滤波。

连续小波变换本质上是求被分析信号与不同尺度的小波之间的卷积。根据时域卷积定理，小波滤波过程可以采用频域相乘的方式进行

WT(f0,β)=F-1{X(f)Ψ*(f)}

(5)

式中:F-1表示傅里叶反变换；X(f)为被分析信号x(t)的傅里叶变换。根据Hilbert变换的性质，复小波滤波所得的复信号WT(f0,β)的实部和虚部互为Hilbert变换对，因此可以直接利用式(5)的结果获取滤波后信号的包络S(t)

(6)

式中：Re和Im分别表示取实部和虚部。复小波滤波的优势之一就在于滤波和解调可以同步实现。

1.2 自适应最优频带选择

由冲击引起的周期性阻尼衰减振动是滚动轴承局部故障的典型特征，也是衡量带通滤波效果的准则。广泛应用作带通滤波器优化目标的Kurtosis只能反映冲击强弱而不能反映冲击的周期性，研究表明Kurtosis随冲击响应周期性增强反而降低[21]。为此作者提出包络谱谱峰因子(EC)，用于同时度量信号中冲击成分的能量大小和周期性规律强弱。

设信号x(t)最优滤波后由式(6)得到的包络信号S(t)的离散形式为S(n)，n=1,2,…,N，N为偶数。可由式(7)得到S(n)的频谱，即最优频带包络谱ENV(m)。

m=0,1,…,N-1

(7)

根据傅里叶变换的性质可知，周期性信号在频谱中表现为高能量的稀疏离散分量，而高斯噪声信号的频谱特性为低幅值的噪声系列(理论上为常数)。因此，包络谱中的最大值ENVmax与均方根值ENVrms之比能近似表示包络谱中周期性成分所占能量比。

ENVmax=max[ENV(m)],

m=0,1,…,N-1

(8)

(9)

包络谱谱峰因子EC定义为

(10)

为了避免与转频相关的故障如齿轮局部故障和转子碰摩等带来的影响，上式中ENVmax与ENVrms分别定义为包络谱ENV(m)在[n×fr,fs/2]范围内的最大值和有效值，其中fr和fs分别表示轴承旋转频率及信号采样频率。对于滚动轴承中常见的内圈和外圈局部故障，其故障特征频率的估计公式分别为内圈BPFI≈0.6×Num×fr，外圈BPFO≈0.4×Num×fr，式中Num为滚动体数量、fr为转频。可见，当滚动体数量大于等于5时，两种故障特征频率均≥2×fr。因此为排除转频等低频成分在包络谱中的影响，在计算包络谱最大值和包络谱均值时可以舍去2×fr之前的频率成分，即n可取为2。对于滚动体数量小于5的情况，n则可直接取0，因为通过对滤波器中心频率f0取值的范围限制，包络谱中转频影响已很小。指标EC越大意味着滤波后信号的周期冲击成分所占比例越大，这由冲击成分的强度和周期性强弱同时决定。

EC用于评价不同的{f0,β}组合的滤波效果及频带内冲击成分的能量比例。设定滤波器中心频率的寻优范围为[k×fr,0.45×fs]，为排除转频故障如转子和齿轮故障的影响，k可取为40，该范围可按线性或对数规律均匀分割，取值点数主要考虑计算量与精度的平衡，实验结果表明100个取值点能得比较满意的中心频率寻优结果。带宽太窄将不足于覆盖冲击故障引起的边频带，太宽又会引入更多的噪声，因此许多文献推荐带宽为三倍的最大故障特征频率[22]。对于外圈固定的滚动轴承而言，其最大故障特征频率通常为内圈故障频率(BPFI)，所以实际上可以固定滤波器带宽为β= 3×BPFI。但是为了进一步确保解调结果的可信度，取β=[3,3.5,4,4.5,5,5.5,6]×BPFI，带宽候选值只有7个，不会过于增加寻优过程计算量。

1.3 自适应频带冲击强度

本文提出自适应频带冲击能量(Shock Value of Selected Frequency Band,SVSB)作为滚动轴承故障量化评估指标，其计算流程如图1所示。首先根据被测轴承的转速和结构参数确定轴承故障特征频率，再结合采样频率并由1.2所述以确定Morlet滤波器中心频率和带宽参数的寻优范围。计算寻优范围内所有{f0,β}组合得到的滤波信号的EC值，其中最大EC值对应的组合即为最优滤波器参数。定义由最优滤波器依据式(5)所得最优滤波信号为Xfiltered(i)，则其均方根值Xf-rms如(12)式所示。

Xflltered(i)=Re[WT(f0,β)],i=1,2,…,N

(11)

式中：Re表示取实部。

(12)

本文提出的自适应频带冲击冲击强度指标SVSB(Shock Value of Selected Frequency Band,SVSB)定义为

SVSB=Xf-rms×EC

(13)

式中:Xf-rms表示自适应选择的频带内信号总强度，EC表明冲击成分所占的比例，因此SVSB有望能反映信号中单纯周期性冲击成分的强弱并定量反映局部故障的严重程度。

图1 自适应频带冲击强度计算流程Fig.1 Procedure of SVSB

2 人工植入故障数据分析

在如图2所示的轴承齿轮故障综合试验台上进行滚动轴承人工植入故障实验，试验台由变频电机通过皮带传动驱动。试验台包括右半部分的齿轮传动部分和本文用到左半部转子轴承故障实验部分。实验轴承型号为NU205EM内圈可拆式滚子轴承，安装在最下端的实验轴承座中。通过电火花加工共模拟了四种不同程度的内圈故障，如图3所示，凹槽宽度分别为0.05、0.17、0.45和1.00 mm。

加速度传感器通过磁座安装在试验轴承座的上方，采样频率为12 000 Hz，轴承内圈转速为1 218r/min，通过螺旋加载结构向转子施加80 kgf的力，可计算滚动轴承内圈故障特征频率BPFI=155.6 Hz。四种不同内圈故障程度各采集3组信号，如图4所示，可以看到随着故障程度的加深，冲击现象越发明显并且幅值有所增大。图5给出了12个信号的RMS值及每种故障程度的RMS均值，可以发现除了1 mm故障程度外，其余三种故障程度之间的区别不大，并且0.45 mm故障程度的RMS总体小于0.17 mm情况，这主要是因为两者故障尺寸相差不大，而0.45 mm时因为冲击明显噪声量减小导致信号总体能量减小。上述现象不利于区别不同故障程度大小并跟踪故障程度的发展。

图2 轴承齿轮综合故障模拟试验台Fig.2 Test rig for bearing and gear fault simulation

图3 不同故障程度的轴承内圈Fig.3 Inner race with different fault

(a) 0.05 mm(b) 0.17 mm

(c) 0.45 mm(d) 1.00 mm

图4 不同程度内圈故障信号
Fig.4 Vibration of diffferent inner race fault severity levels

图5 不同程度内圈故障信号的RMS值Fig.5 RMS values of different inner race fault levels

为此对各信号进行最优Morlet小波滤波，利用EC值最大确定最优滤波频带，最终得到的最优滤波器带宽均为带宽参数寻优范围的下限即3×BPFI，因为带宽过大将使EC值的分母增长速度大于分子，从而EC值下降。所得最优滤波器中心频率值如图6所示，可见除0.05 mm故障外，其余各组内信号的中心频率相差不大，但各组间中心频率值存在一定差距，说明针对信号本身进行滤波器优化的必要性。图6中各中心频率数据点处竖线长度表示最优滤波器带宽值。0.05 mm故障对应的三组数据中最后一组的中心频率与前两组差别较大，可能是因安装轴承时预紧力大小不一致造成轴承系统固有频率存在差异。利用得到的最优滤波器对图4中的各信号进行最优带通滤波，结果如图7所示，可见信号中噪声得到了进一步的消除，冲击特征得以增强。

图6 不同故障程度信号的最优滤波器中心频率f0Fig.6 The optimal f0 of the signals of inner race faults

计算图7中各最优滤波信号的RMS与EC值，其乘积即为本文提出的自适应频带冲击强度指标(SVSB)。SVSB结果如图8所示，可以看到图5中RMS不能很好区分的0.17 mm和0.45 mm两种故障情况在此得到了很好的辨识，后者的3个样本值及平均值均大于前者。且随着故障程度的增长，SVSB值逐步增长，各不同故障程度的SVSB取值范围之间不存在重叠，且差别较大，利于不同故障程度的辨识和故障发展趋势的跟踪。

图4原始信号的RMS和图7中最优滤波信号的RMS、Ec和SVSB值详细结果如表1所示，从中可以看到各参数随故障程度的变化情况。

(a) 0.05 mm(b) 0.17 mm

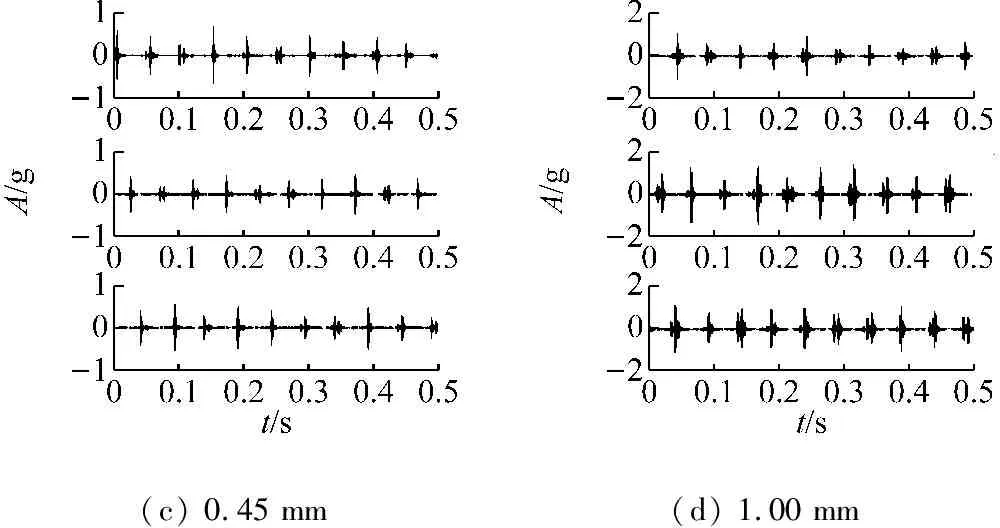
(c) 0.45 mm(d) 1.00 mm

图7 不同程度内圈故障信号的最优滤波结果
Fig.7 Filtered signals of different inner race fault levels

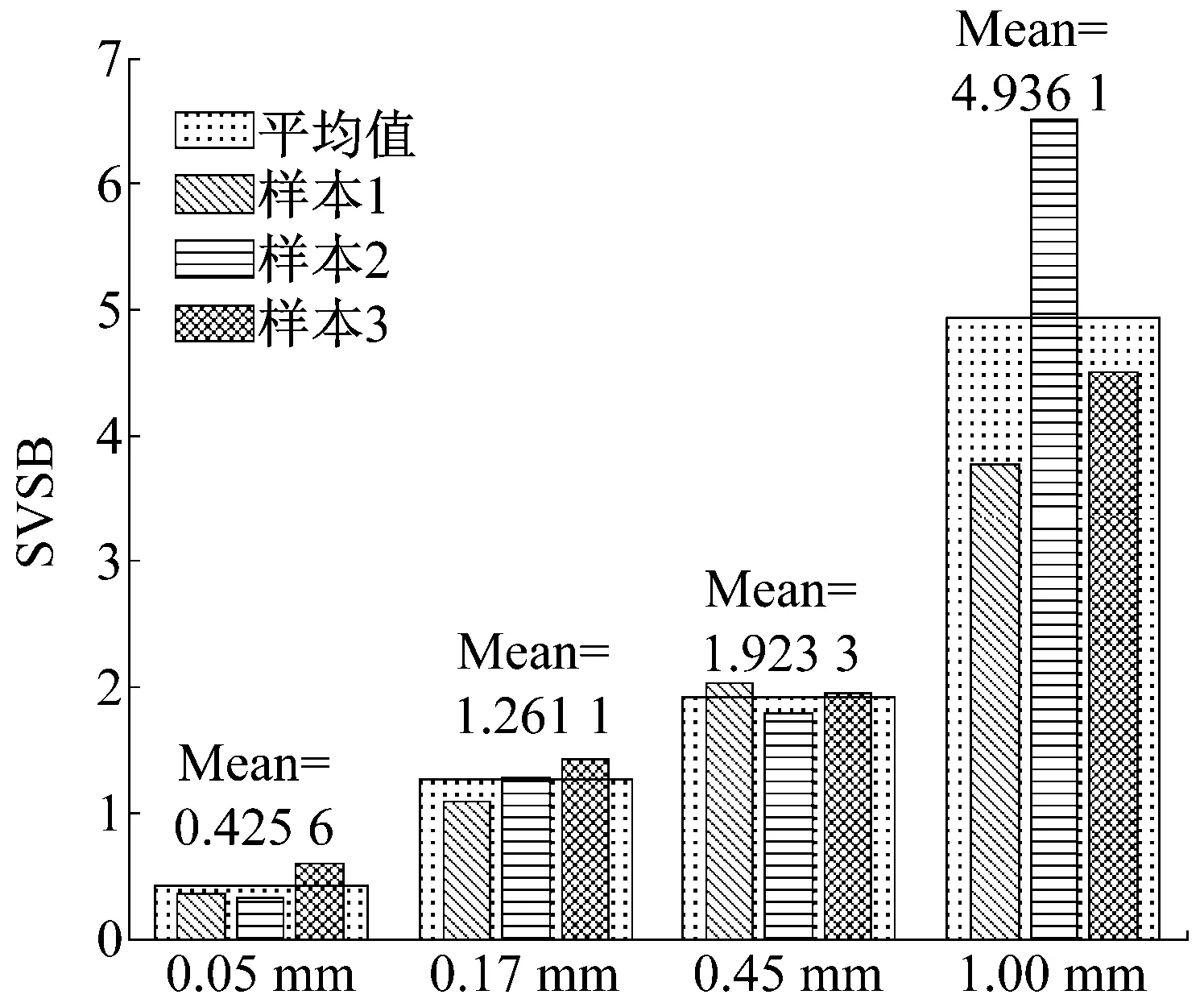
图8 不同程度内圈故障信号的SVSB值Fig.8 SVSB values of various inner race fault levels

3 疲劳试验数据分析

上述内圈故障是人为加工制造的，不能完全反映真实使用过程中滚动轴承故障发生发展过程。为了验证本文方法在自然故障演化过程中的早期诊断及跟踪能力，对滚动轴承疲劳试验数据进行分析。实验数据来源于美国辛辛那提大学智能维护中心，图9(a)是滚动轴承疲劳试验台的整体结构示意图，图9(b)是试验台局部照片[23-24]。

电动机通过皮带传动驱动主轴以2 000 r/min的转速旋转。主轴上安装有四个型号为Rexnord ZA-2115的双列滚柱轴承，其中两端的轴承固定在机体上，中间的两个轴承通过杠杆机构向主轴施加径向载荷。由转速及轴承结构参数可知内圈故障特征频率BPFI = 297.9 Hz。疲劳试验于2004.02.12 10:32:39开始至 2004.02.19 06:22:39结束，最终解体发现轴承1发生了严重外圈故障。试验过程中通过安装在轴承座上的加速度传感器以20 000 Hz的采样频率每隔10 min采集振动信号一次，共采集到984个数据文件，每个文件包含4列长为20 480点的数据，本文分析的是第一列。计算984组原始信号的RMS值，结果如图10，故障发生最为明显的时刻为703，此时RMS存在阶跃。仔细观察可以发现RMS曲线在No.534和No.703之间，近似按线性规律逐步增大，但是534时刻RMS值为0.084 3，较之前533时刻的0.081 0增长幅值较小，增长比例仅为4.07%，不利于早期故障检测。

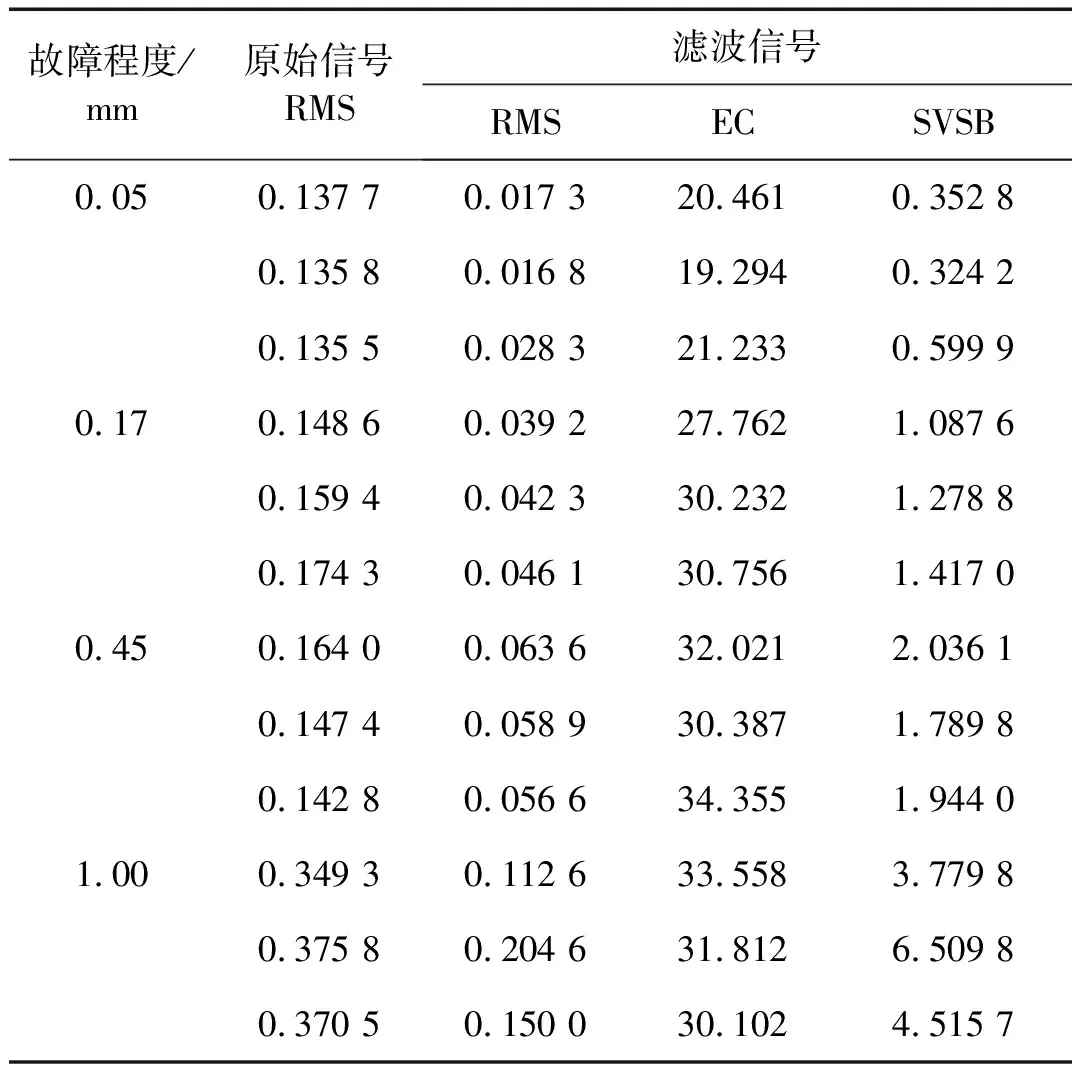
表1 人为植入内圈故障信号各参数计算结果Tab.1 Parameters of original and filtered signals of

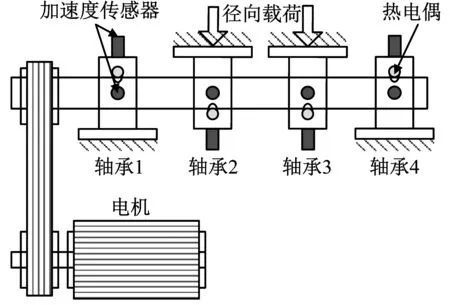
(a) 整体示意图

(b) 局部照片

图10 原始振动信号RMS值Fig.10 RMS of original vibration signals

观察图10的RMS曲线可以发现，轴承性能退化过程存在不断重复出现的“故障出现—劣化—磨平”现象。如534～703时刻即可视作故障出现并劣化的过程，而703～786则是故障剥落点被逐步磨平，冲击变小。786～850过程中剥落点在原基础上再次产生并劣化，之后至900时刻再次磨平。整个过程都是剥落点在原来基础上重复出现和磨平，所以故障总体上在波动中增大，因此RMS虽然存在波动，但总体呈增大趋势。疲劳试验过程中典型时刻的时域波形图如图11所示，可以看到对应RMS值较小的时刻，如534的早期故障时刻、786和900的剥落被磨平时刻，信号中冲击成分并不明显。本文疲劳试验台结构单一，所采集的振动信号受外界干扰小，因此RMS反映的信号总体强度水平基本上由信号中的冲击强度所决定，即RMS在一定程度上反映了信号的冲击强度。

对疲劳试验过程的984组信号进行最优Morlet小波滤波，所得最优滤波器宽度均为3×BPFI，最优中心频率则如图12所示，可以看到中心频率在早期故障发生时刻534处存在大幅度变化。计算各滤波信号的RMS和EC值，其乘积即为本文提出的自适应频带冲击强度(SVSB)，结果如图13。将SVSB与RMS相比较，可以得出如下结论：① 534时刻的SVSB相对于533时刻的增幅为209.5%，存在明显陡峭的增幅，因此相比RMS更便于早期故障检测；② 存在和RMS类似的故障反复出现-磨平现象，说明SVSB同样能跟踪轴承性能劣化过程。同时SVSB的故障出现-磨平过程波动幅度较RMS大，说明SVSB能以更为明显的趋势描述故障劣化过程。典型时刻的最优滤波结果如图14所示，相对图11可以看到噪声得到抑制且冲击特征明显增强。

(a) No.534

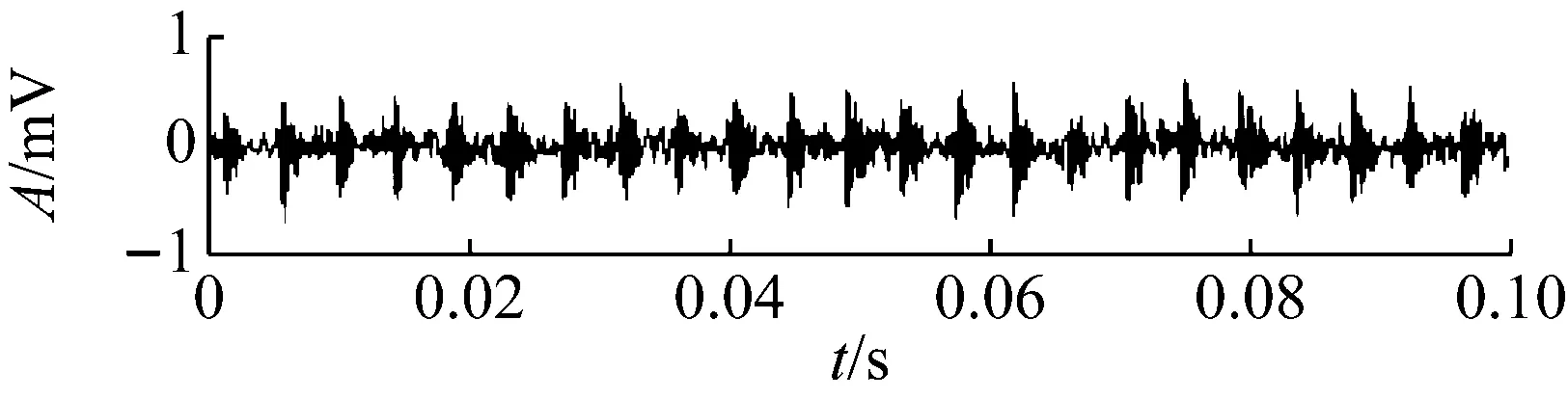
(b) No.703

(c) No.786

(d) No.850

(e) No.900

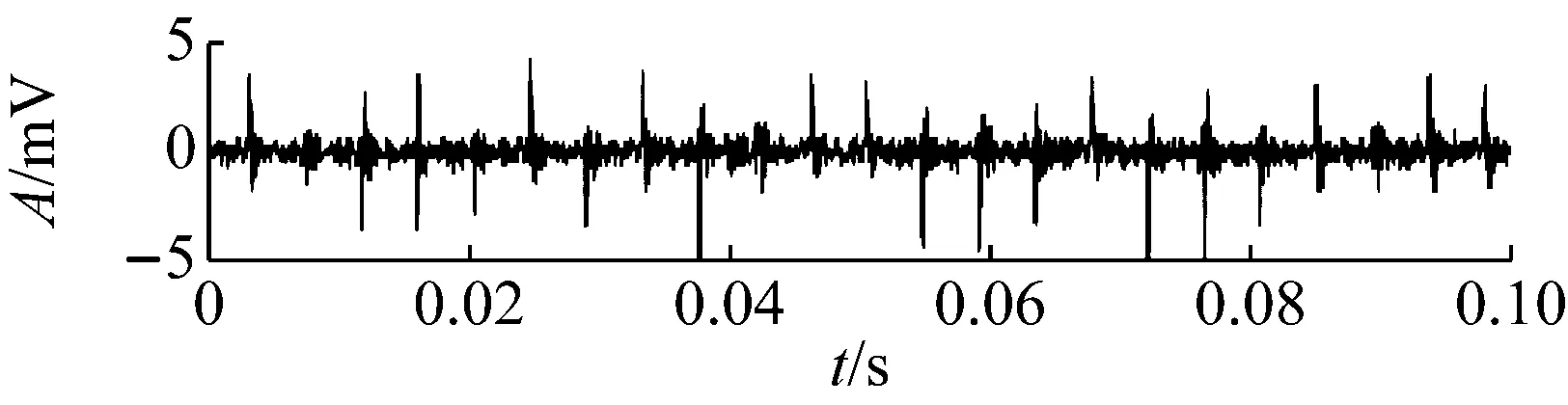
(f) No.980

图12 疲劳试验滤波器最优中心频率f0变化过程Fig.12 Optimal center frequency (f0) of run-to-failure test

若将滤波器中心频率固定在某一个值如自适应滤波中680时刻对应的中心频率4 636.2 Hz，则所得SVSB结果如图15所示。可以看到相比于自适应滤波对应的图13所示的SVSB，图15的早期故障检测能力明显降低，说明了自适应选择滤波频带的必要性。

图13 疲劳试验过程SVSB值Fig.13 SVSB of run-to-failure test

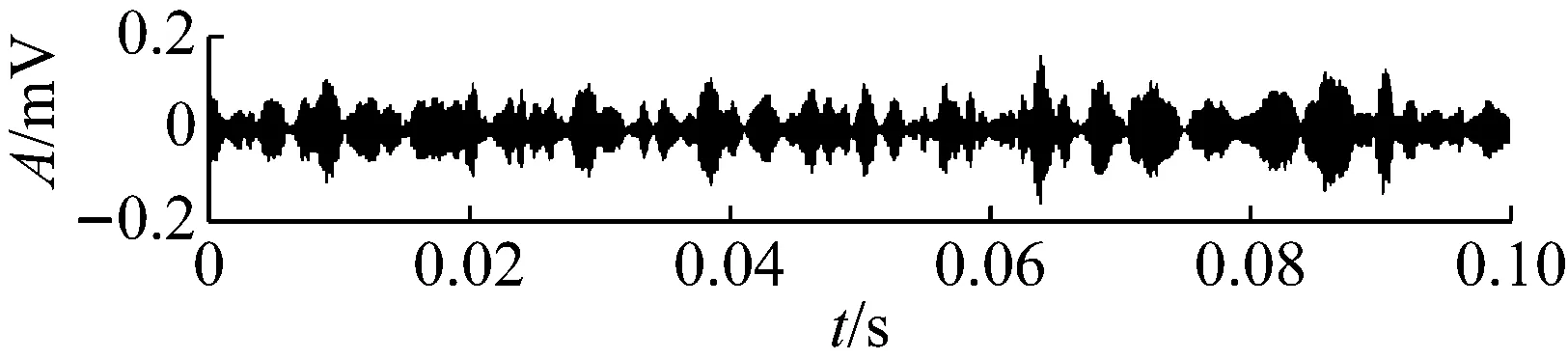
(a) No.534

(b) No.703

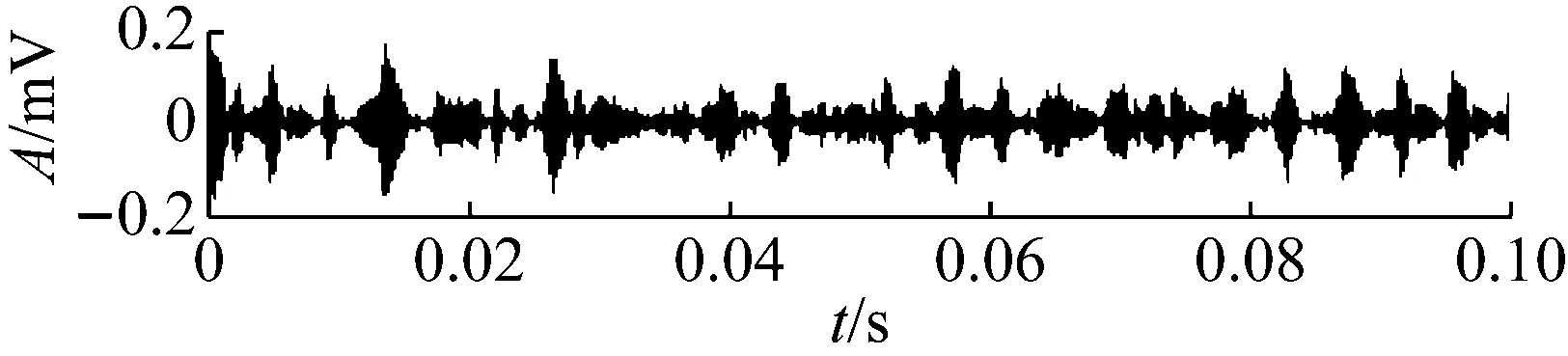
(c) No.786

(d) No.850

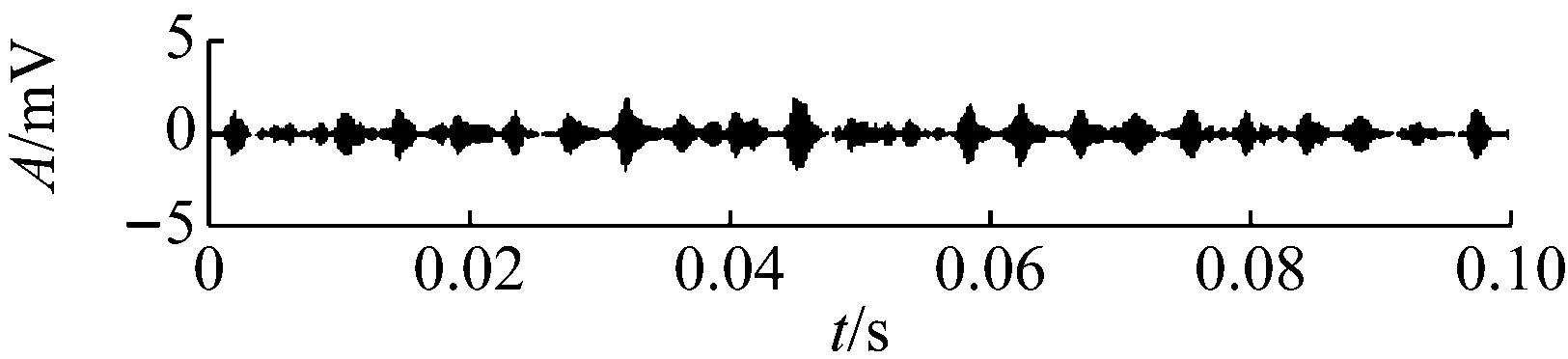
(e) No.900

(f) No.980

图15 滤波器中心频率固定为f0 (680)时的SVSBFig.15 SVSB with keeping f0 equal to f0 (680) = 4 636.2 Hz

4 结 论

故障量化评估是剩余寿命预测和状态维修的基础，故障量化指标应具有计算简单、早期故障检测能力强及与故障发展趋势一致性好等优点。针对常规时域方法如均方根值(RMS)不能及时发现早期故障而基于空间距离和概率相似度的评估方法存在算法过于复杂低效等问题，本文提出了一个新的故障量化评估指标——自适应频带冲击强度(SVSB)。SVSB是指利用自适应复平移Morlet小波对信号进行自适应带通滤波之后，滤波信号的RMS与其包络谱谱峰因子(EC)的乘积。SVSB中RMS指带通滤波后信号的总体强度，而Ec表示其中冲击分量所占比例，因此SVSB能有效反映信号中单纯冲击分量的强度，有望为滚动轴承局部冲击类故障评估补充一种新方法。

利用人工植入的离散故障程度轴承内圈数据和外圈故障疲劳试验数据验证了本文方法的有效性，并与常规RMS进行对比凸显了本文方法的优越性。