基于ITD与稀疏编码收缩的滚动轴承故障特征提取方法

余建波，刘海强，郑小云，周炳海，程 辉，孙习武

(1.同济大学 机械与能源工程学院,上海 201804；2.上海航天设备制造总厂,上海 201100)

滚动轴承是机械设备最为关键部件之一，轴承的缺陷和损伤将直接影响设备稳定运行甚至造成整个设备的损坏[1]。点蚀、裂纹等原因使得轴承在运行时产生具有一定周期的冲击信号[2]，而故障信号的频率特征能够反映轴承的故障类型。文献[3]表明旋转机械故障产生的振动信号的概率分布函数往往具有稀疏分布的特征，但是这些特征往往会被背景噪声所淹没。因此，在强背景噪声下振动信号冲击特征的有效提取是滚动轴承故障诊断的关键。

时频分析法是处理非线性、非平稳信号的常用方法[4-5]。如短时傅里叶变换(Short Time Fourier Transform,STFT)、小波变换(Wavelet Transform,WT)、经验模态分解(Empirical Mode Decomposition,EMD)、局部均值分解(Local Mean Decomposition,LMD)等[6]能同时从时域和频域揭示信号成分，在机械故障诊断中取得了广泛应用。短时傅里叶变换方法简单高效，但受Heisenberg不确定原理的限制，时频分辨率较低。小波变换具有可变的时频窗口，但要求选择基函数，有限的时宽也有可能导致能量泄漏。EMD基于信号本身的局部特征时间尺度，虽有很大发展，但还存在端点效应、模态混叠和负频率等问题。相对于EMD而言，LMD在端点效应和负频率方面的改进较为明显，但计算速度较慢，也会出现虚假分量。固有时间尺度分解(Intrinsic Time Scale Decomposition,ITD)是由Frei提出的一种自适应时频域分析方法[7]，其分解过程不会出现过包络和欠包络现象，同时端点效应被严格限制在两端。最近，ITD在故障诊断中得到了有效的应用。罗颂荣等[8]用ITD将原始信号分解成若干个PR分量，提取第一个PR分量的无量纲时域统计参数组成故障特征向量。杨宇等[9]提出内禀尺度分量( Intrinsic Scale Component，ISC)的定义，采用改进的ITD算法有效地识别转子的故障类型。张小龙等[10]通过提取由ITD分解得到的PR分量的Lempel-Ziv 复杂度作为特征向量，然后利用支持向量基(Support Vector Machine，SVM)识别出轴承的故障类型。

稀疏编码收缩(Sparse Code Shrinkage，SCS)是Hyvarinen[11]提出的一种基于最大似然估计的降噪方法，该方法不但成功地应用于稀疏性分析和图像降噪[12]，而且应用到机械设备故障信号诊断中。Fyfe等[13]利用稀疏编码收缩中的极大似然估计作为小波阈值降噪的软阈值函数，可识别出齿轮故障，但是其没有前置滤噪单元，导致稀疏编码收缩降噪效果不佳。Wang等[14]通过SCS和小波包相结合的降噪方法滤除裂纹信号包含的噪声。

针对滚动轴承故障信号具有周期性冲击的特点和经常被背景噪声所淹没的问题，本文提出了一种基于ITD与SCS集成的轴承故障特征提取方法(命名为ITD-SCS)。ITD分解得到的PR分量保留了原始信号的冲击特性；奇异值分解(Singular Value Decomposition,SVD)可滤除PR分量含有的噪声并提高其稀疏性；SCS能有效提取稀疏信号的主要冲击部分。通过仿真信号和轴承振动数据的分析以及与经典的基于多尺度的滤噪方法对比验证了本文所提方法在轴承故障诊断的可行性和优越性。

1 固有时间尺度分解

对于任意信号Xt，定义L为基线信号提取算子，Xt可以作如下分解

Xt=LXt+(1-L)Xt=Lt+Ht

(1)

其中Lt=LXt是基线信号，Ht=(1-L)Xt是一个固有旋转分量。

假设{Xt,t≥0}是一个实值信号，{τk,k=1,2,…}代表Xt的局部极值点所对应的时刻，为方便起见定义τ0=0。如果Xt在某一个区间有恒定值，考虑附近的信号存在波动，仍然认为Xt在这个区间包含着极值，选择τk为此区间的右端点。为了简化符号，记Xk=X(τk)，Lk=L(τk)。

假设Lt和Ht在区间[0,τk]上有定义，Xt在[0,τk+2]上有定义。我们可以在区间(τk,τk+1]上的连续极值点之间定义一个分段线性的基线信号提取算子L，即：

(2)

其中t∈(τk,τk+1]，

同时0<α<1，一般取α=0.5。

定义了基线信号之后，我们可以定义一个固有旋转分量提取算子H，即：

(3)

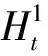
(4)

2 ITD-SCS方法

ITD可把信号分解成频率和幅值都依次降低的几个PR分量和一个基线分量L。前几个PR分量既包含较多的冲击信号特征，又混有大量的噪声。充分考虑ITD与SCS方法在振动信号处理应用中的要求和优点，针对轴承故障信号提出一种基于ITD与SCS集成的轴承故障特征提取方法。ITD-SCS流程如图1所示，其中s表示SVD重构阶次，m为Hankel矩阵的秩，其具体运行步骤如下：

(1) 对采样信号进行ITD分解，得到多个PR分量和一个基线分量L，计算每个PR分量的加权峭度值，选择指标大的若干个PR分量作为后续研究对象；

(2) 对每一有效PR分量构造相应的Hankel矩阵，进行SVD分解，对于每一个Hankel矩阵迭代重构阶次进行SVD重构并计算其峭度值，选择峭度值最大的重构信号为最终PR重构信号；

(3) 合成所有经过SVD重构的PR分量，采用SCS提取重构信号的冲击特征，对提取的冲击信号进行包络谱分析，实现轴承故障诊断。

图1 ITD-SCS故障特征提取流程Fig.1 ITD-SCS fault diagnosis flow chart

2.1 固有旋转分量选择

峭度[15]是反映信号分布特性的无量纲统计参量，可以描述信号中冲击成分所占比重的大小

(5)

式中:σ和μ分别表示信号的标准差和均值;E(t)表示变量t的数学期望。虽然峭度能够描述信号中冲击成份所占比重的大小，但是峭度并不能描述每一个尺度函数中其冲击成份占总信号的权重比。因此用峭度来选择ITD分解后的PR分量是不合理的。本文提出一种加权峭度的指标来选取有效的尺度分量，其可以表示为

PW=K×AM

(6)

2.2 奇异值分解降噪

有效PR分量既包含故障冲击特征又混有高频噪声，大量的噪声会导致故障特征难以提取。考虑到SVD可将信号分解为加噪信号子空间和噪声信号子空间，通过选择有效的重构阶次可将噪声信号子空间去除掉，本文选择SVD对信号进行降噪，作为SCS的前置处理，以提高信号的稀疏性。

对于一个实矩阵A∈Rm×n,无论其行列是否相关，必定存在正交矩阵U∈Rm×n和正交矩阵U∈Rm×n，使得下式成立

A=UDVT

(7)

式中:D是对角阵，D∈Rm×n，表示为D=(diag(σ1,σ2,…,σq),0)(m≤n)或其转置(m>n)，0表示零矩阵，q=min(m,n)，且有σ1≥σ2≥…≥σq>0即矩阵A的奇异值。

对于一个单独的一维信号序列，为了利用SVD对其进行处理，必须构造出一个矩阵。设有离散信号y(i)，i=1,2,…,N，N为信号的长度，利用此信号可以构造矩阵如下

A=

S+W

(8)

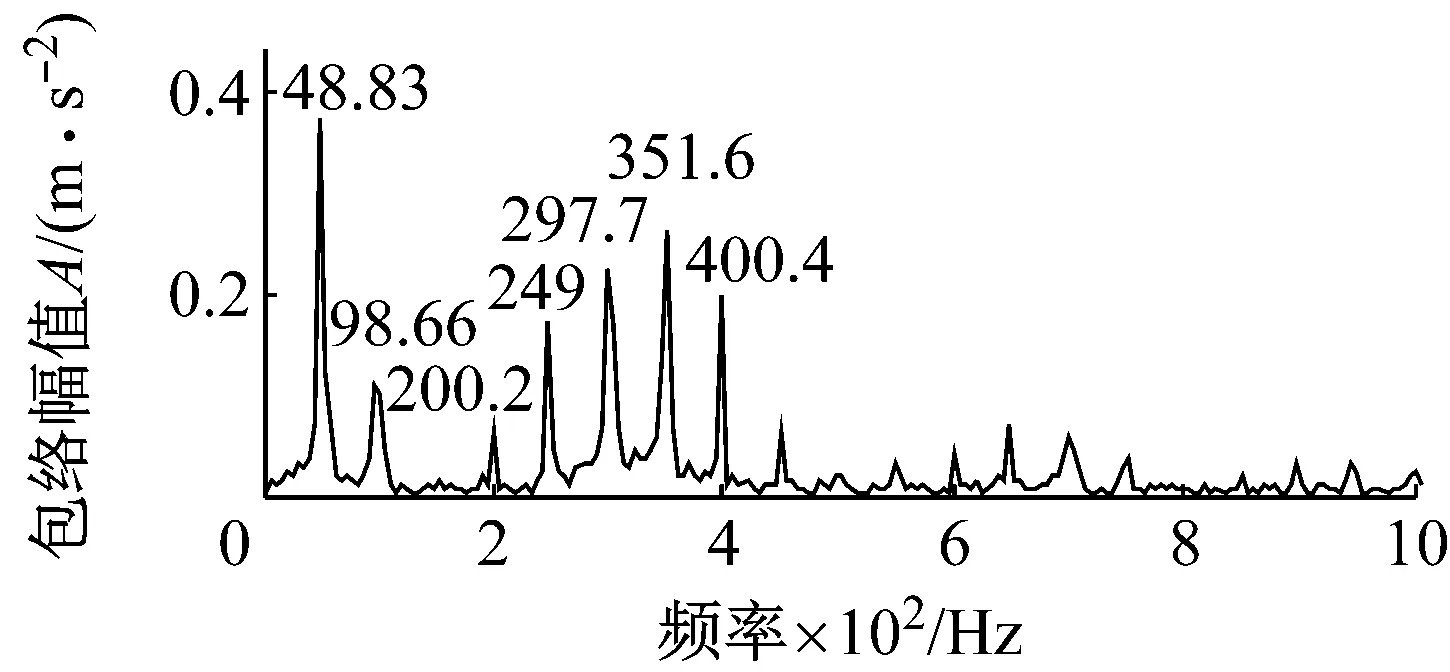
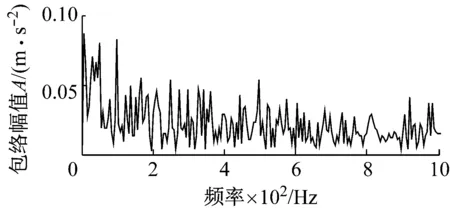
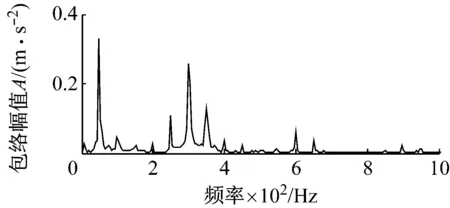
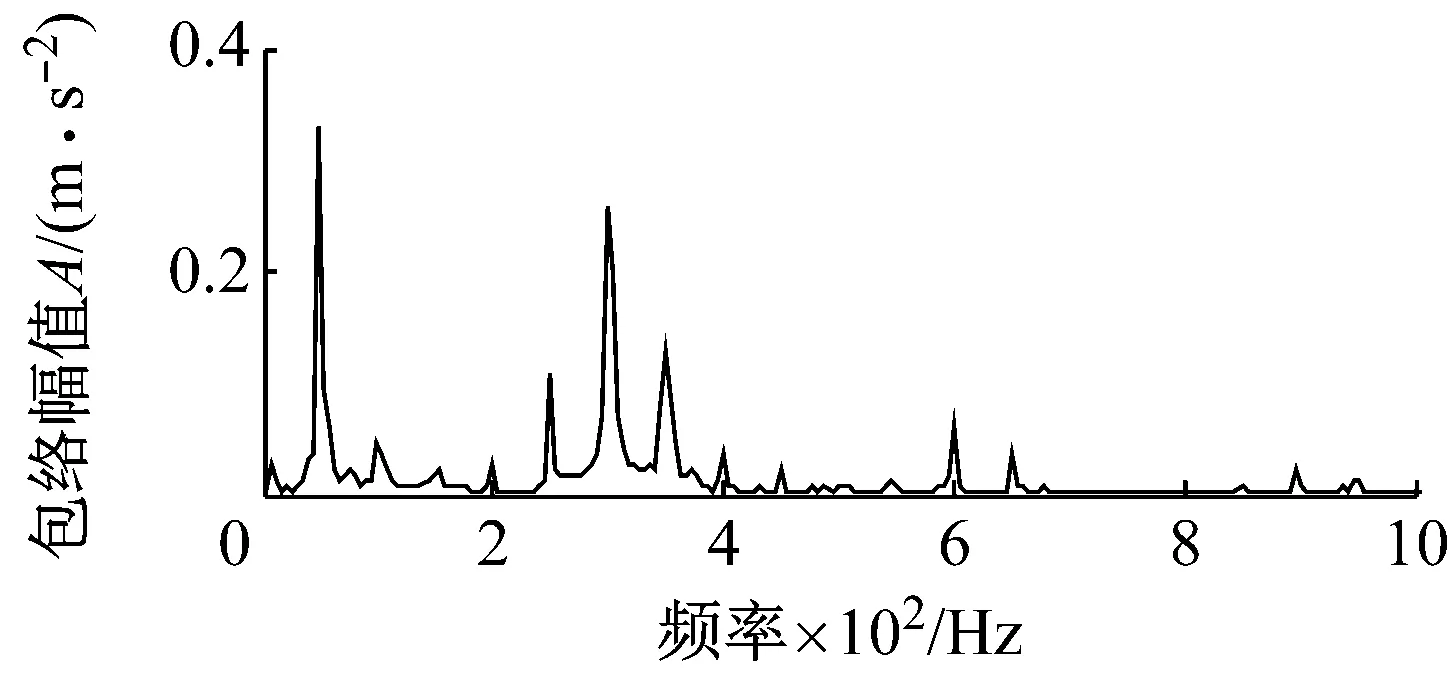
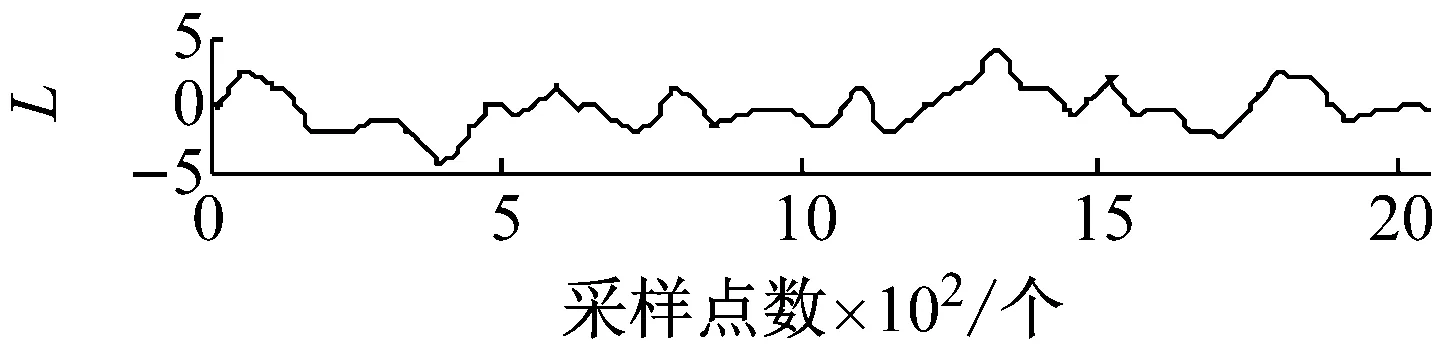
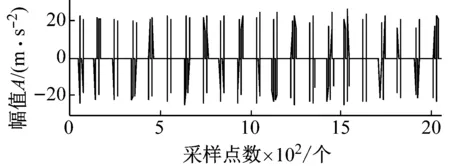
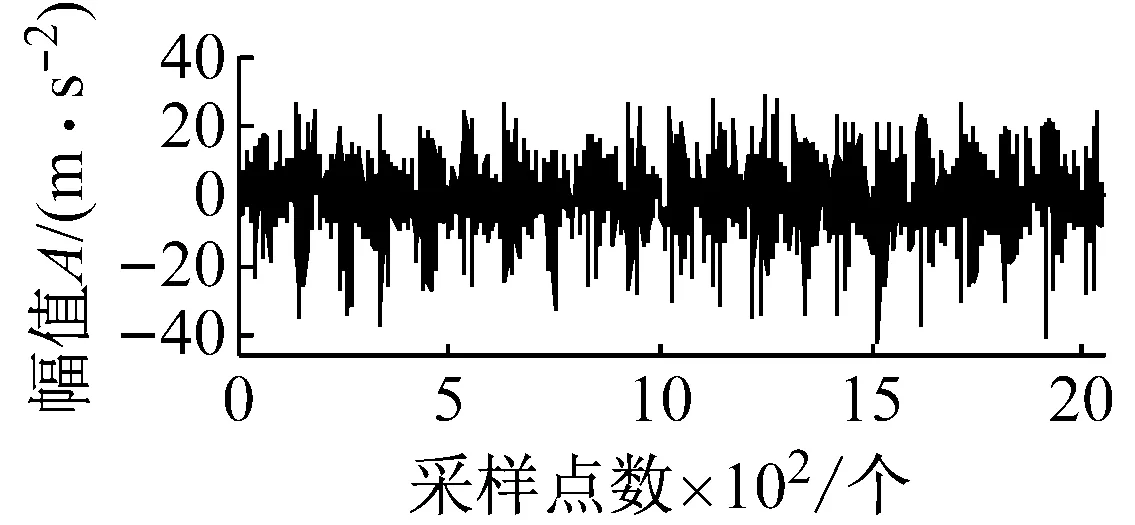
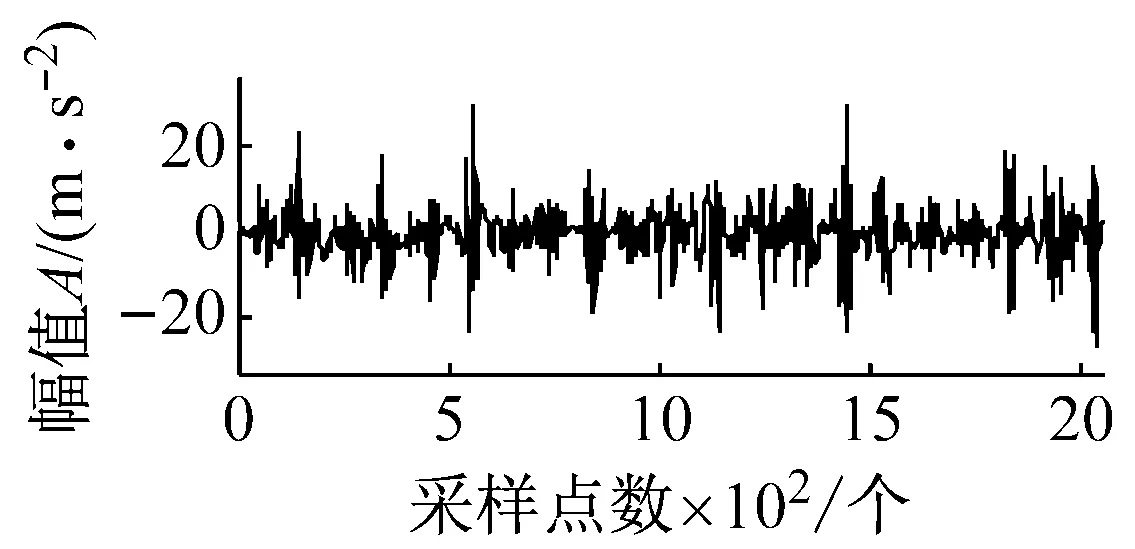
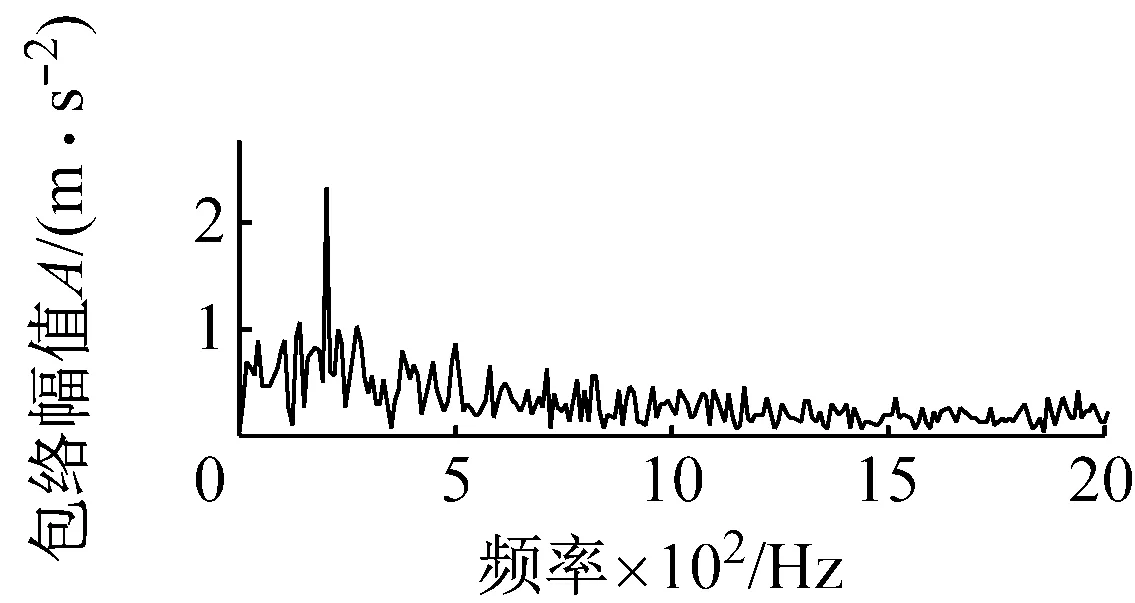
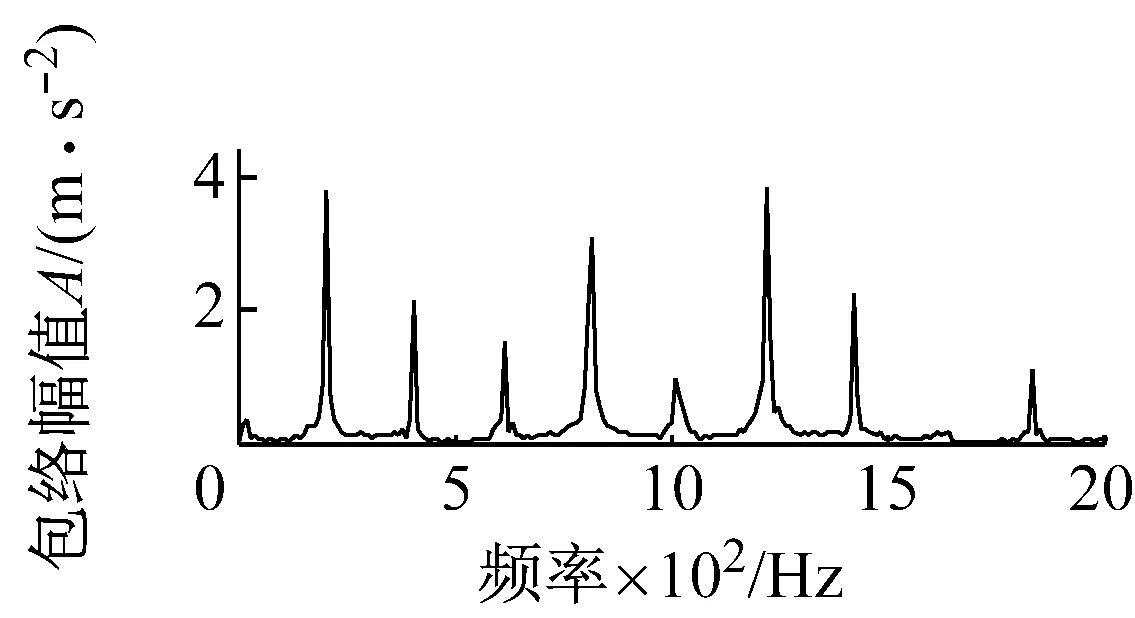
式中: 1

最后，本文对每一有效PR分量构造的Hankel矩阵通过迭代重构阶次重构PR分量并计算重构信号的峭度值，选择峭度达到最大时对应的重构信号为最终的PR重构信号。将所有经过SVD重构的信号进行相加得到新的合成信号。

2.3 基于SCS的故障冲击特征提取

经过SVD重构的信号滤除了大量的噪声，同时其稀疏性也得到增强，但是通常会包含一定的噪声，即SVD重构过程中不为零的奇异值对应子信号包含的噪声仍然存在，可能导致信号的冲击特征并不显著。为了进一步去除SVD重构过程中包含的噪声并提取冲击特征，本文提出了基于SCS的信号冲击特征提取方法。其主要原理如下

假设x是原振动信号，v是均值为0，方差为σ2的高斯白噪声,则测量信号为

y=x+v

(9)

当轴承单元产生故障时，其振动信号x通常表现出强烈的超高斯特征。采用如下概率密度函数来模拟超高斯信号(Super-Gussian Signal)

(10)

式中:d是x的标准差;α为一个控制着概率密度函数的稀疏性的常数。对于冲击信号的概率密度函数，文献[13]建议设α为1，同样适合本文。

(11)

(12)

式中:σy是y的标准差。

3 仿真分析

为了验证ITD-SCS的有效性，对轴承内圈故障仿真信号加以分析，并与典型的多尺度滤噪方法WTD-SVD[17]、EMD-WTD[18]与EMD-SVD[19]进行比较。图2(a)给出了一个轴承内圈故障仿真信号，其故障频率为50 Hz，冲击信号周期为200，初始相位为零。图2(b)为仿真信号添加均值为零的高斯白噪声的含噪信号。从图2(b)可以看到轴承故障信号已经被噪声淹没，很难发现相关的故障特征。

(a) 轴承内圈故障仿真信号

(b) 加噪后的仿真信号

图3为经过各种方法滤噪后的信号及相应的包络谱。从图2(a)中可以看出，该仿真信号三个相邻最大的峰值之间的间隔为30个采样点，每次冲击间隔为

(a) ITD-SCS

(b) WTD-SVD

(c) EMD-WTD

(d) EMD-SVD

200个采样点。在图3(a)中也可得知其相邻三个最大峰值之间的距离是30个采样点，每一次冲击间隔为198或者202个采样点，说明每间隔198或者202个采样点，就会产生一次故障冲击。从图3(b)、(c)和(d)可以看出，在时域方面WTD-SVD、EMD-WTD与EMD-SVD三种方法都没有很好地滤除故障信号中的噪声，提取故障冲击特征。在频域方面WTD-SVD和EMD-WTD的包络谱图中有很多高频峰值且没有提取故障倍频，EMD-SVD的包络谱虽然呈现倍频，但是其倍频峰值明显低于本文方法的倍频峰值。综上，ITD-SCS能够有效滤除噪声，提取故障的冲击特征，从时频域诊断出该故障为轴承内圈故障，提取效果整体优于其他方法。

4 实例分析

为了进一步验证本文所提方法的有效性，采用实际运行状态下轴承从正常到最终失效的全寿命振动数据作实例分析。加速轴承寿命试验机(ABLT-1A)由杭州轴承试验研究中心提供。它由交流电机驱动，在同一根轴上同时进行四个轴承的寿命试验。试验台总体如图4所示，轴承各参数如表1和表2所示。

表1 轴承结构参数Tab.1 Structure parameters of bearing

表2 轴承外圈故障数据Tab.2 Fault data of outer race

图4 轴承试验台Fig.4 Bearing test bed

对轴承外圈故障失效的样本进行研究。测试过程每隔10 min进行数据采样，每次采样2 048个数据点。该轴承整个寿命共经历了119个采样周期，取轴承全寿命测试过程中出现早期故障特征时的一组振动信号进行分析(即第105个采样周期)。图5(a)为采集的故障信号时域波形图，波形较复杂且伴有大量噪声，仅通过时域波形无法了解故障信息。从图5(b)的幅值谱也可以看到，由于故障冲击的作用，系统的固有频率已被激起，但由于噪声的影响，频率集中在中、高频处，而故障诊断所关注的低频段的故障频率难以观察到，因而从幅值谱图中也难以诊断出轴承的故障类型。

(a) 外圈故障信号时域波形

(b) 外圈故障信号幅值谱

图6呈现了对故障信号进行ITD分解得到4个PR分量和一个L分量。每个PR分量对应的加权峭度值指标的计算结果如表3所示，选择加权峭度值大的PR1与PR2分量。ITD分解得到PR1与PR2分量增强了信号的冲击特征，但是还存在大量的噪声。对每个PR分量构造Hankel矩阵进行SVD分解，有效重构阶次选择重构阶次对应峭度值最大的阶次，图7为PR1每一重构阶次和对应的峭度值，重构阶次为25时重构的信号具有最大峭度值，得到重构信号如图8(a)所示。图8(b)为PR1和PR2分别经过SVD降噪后的合成信号。通过PR分量选择和SVD重构进一步提高了信号的稀疏性。最后，SCS提取合成信号的周期性冲击特征，如图9(a)所示，可以清晰地看到周期性的冲击特性，共包含了21次明显的冲击。可以看出同一冲击相邻峰值之间的距离为17个采样点，相邻冲击之间的距离为97或98个采样点，从而有故障周期约为0.004 85～0.004 9 s，可知故障频率为204.08 Hz和206.185之间。

同时对提取的细节信号进行包络谱分析，如图9(b)所示，可以看到中高频率成分得到了抑制，频率峰值集中在低频处，205.1 Hz、410.2 Hz、820.3 Hz、1 016 Hz、1 426 Hz等峰值频率均是205.29的近似倍频，故障频率以及其倍频的谱线清晰且突出。

图10(a)、(b)和(c)分别为WTD-SVD、EMD-WDT、EMD-SVD诊断轴承故障信号的结果图。四种方法滤澡结果的包络谱都能够提取出故障频率为205.1 Hz。ITD-SCS和EMD-SVD方法提取了故障的倍频410.2、615.3等倍频，另外两种方法没取得较好倍频提取效果。ITD-SCS在故障频率的幅值明显高于EMD-SVD方法求取的幅值。四种方法有效性从时域冲击特征提取，1倍频幅值和2 000 Hz内频率主要峰值为故障倍频的次数三个方面进行了比较，如表4所示。可知，ITD-SCS能够有效滤除信号中含有的随机噪声，并提取故障的周期性冲击特征，提取效果整体优于其他方法。

图6 外圈故障信号ITD分解结果Fig.6 The ITD results of outer race fault signal

表3 PR分量的加权峭度值Tab.3 Weighted Kurtosis of each PR

图7 PR1 重构阶次峭度值Fig.7 Kurtosis reconstruction of order

(a) PR1的SVD滤噪结果

(b) SVD滤噪后重构信号

(a) 时域波形图

(b) 包络谱

表4 四种方法分析结果比较Tab.4 Comparison of analysis results of four methods

(a) WTD-SVD

(b) EMD-WTD

(c) EMD-SVD

5 结 论

滚动轴承故障信号通常具有周期性冲击的特点，且经常被复杂的噪声所淹没，难以在早期及时有效地提取故障特征。本文提出了一种固有时间尺度分解和稀疏编码收缩集成的强背景噪声下信号冲击特征提取方法。该方法首先对振动信号采用ITD分解，获得多个PR分量。以加权峭度值为指标，选择有效的PR分量，突显信号的冲击特征。以SVD作为SCS的前置滤噪单元滤除每个有效PR分量的噪声，从而保留振动信号的冲击特征并提高信号的稀疏性。最后采用SCS提取出振动信号的冲击特征。ITD-SCS与其他典型多尺度滤噪方法(包括WTD-SVD、EMD-WDT和EMD-SVD)在仿真和轴承振动信号比较结果表明，ITD-SCS能有效提取弱故障信号的冲击特征实现故障诊断，并且诊断效果优于其它方法。