平头弹正侵彻单层和多层钢靶的SPH模拟和解析分析
2018-10-20肖毅华董晃晃周建民
肖毅华,董晃晃,周建民
(华东交通大学 机电与车辆工程学院,南昌 330013)
金属材料在防护结构中应用广泛,研究其抗侵彻性能具有重要意义。多层金属靶的抗侵彻性能受到国内外研究者的广泛关注。人们通过实验、数值模拟和解析方法等途径开展了相关研究,取得了一些重要成果。Woodwarda等[1]开展了2024-T351铝合金靶的侵彻实验,结果显示:对于平头弹,多层靶的弹道极限速度高于等厚度单层靶,且厚度组合(即各层的厚度及其顺序)对双层靶的抗侵彻性能有重要影响,当前后层等厚时弹道极限速度最高,然后依次为前厚后薄和前薄后厚;对于锥头弹,多层靶的弹道极限速度随层数和厚度组合不同可能高于也可能低于单层靶。Gupta等[2]进行了低碳钢靶和铝靶的正、斜侵彻实验,结果表明:当组成双层靶的板较厚时,双层靶的抗侵彻性能与等厚度的单层靶差不多,而当板较薄时双层靶的抗侵彻性能低于单层靶;另外,接触式多层靶的抗侵彻性能高于间隙式多层靶。Corran等[3]进行了低碳钢靶的侵彻实验。结果表明:双层靶中两层板的排列顺序对其抗侵彻性能有重要影响,前薄后厚的双层靶优于相反组合的双层靶;同时,多层靶相对于等厚度单层靶的好坏与靶板总厚度有关;另外,接触式多层靶较间隙式多层靶有一定优势。郝鹏等[4]采用轻气炮实验和数值模拟研究了2A12铝合金靶抗卵头弹侵彻的性能,结果表明:接触式双层靶的弹道极限速度高于间隙式双层靶,但都低于单层靶;同时,靶板结构对抗侵彻性能的影响随着弹体侵彻速度的增加而减小。Dey等[5]通过实验和数值模拟研究了平头和卵头弹侵彻Weldox 700 E钢靶的过程。结果表明:对于平头弹,接触式和间隙式双层靶的弹道极限速度高于单层靶,而对于卵头弹则相反。Teng等[6]模拟了不同质量的平头和锥头弹侵彻Weldox 460 E钢靶的过程,发现:对于平头弹,双层靶的抗侵彻性能优于同重量的单层靶,而对于锥头弹,双层靶的抗侵彻性能略差于单层靶。Iqal等[7]模拟了卵头弹侵彻1 mm厚1100-H12铝靶和锥头弹侵彻12 mm厚Weldox 460 E钢靶的过程,结果表明:对于两种靶板材料,单层靶的抗侵彻性能都略高于等厚度的双层靶。Flores-Johnson等[8]采用LS-DYNA模拟了直径7.62 mm的APM2弹侵彻Weldox 700 E钢靶和7075-T651铝合金靶的过程。结果显示:单层靶的抗侵彻性能优于同材料、等厚度的多层靶。Xiao等[9]采用SPH数值模拟和解析方法研究了锥头弹侵彻Weldox 460 E钢靶的过程,系统地分析了靶板的层数、总厚度和厚度组合对多层靶抗侵彻性能的影响。
综上可见,多层靶的抗侵彻性能受很多因素影响,包括弹体形状、靶板厚度、厚度组合、间隙等,且对于不同材料的靶板这些因素的影响可能不同,因此其研究十分复杂。本文针对Weldox 460 E钢靶,采用光滑粒子流体动力学[10](SPH)方法开展了平头弹正侵彻单层和多层钢靶的模拟,系统地分析了靶板的层数、厚度和厚度组合对多层靶抗侵彻性能的影响。同时,建立了预测多层靶弹道极限速度的解析模型,将解析模型与SPH模拟预测的弹道极限速度进行了对比。
1 SPH方程
本文研究平头弹正侵彻钢靶过程。由于问题具有轴对称特性,采用二维轴对称SPH方法进行求解以节省计算时间。计算使用的SPH程序为自编程序。采用的轴对称SPH基本方程为杨刚等导出的具有对称形式的方程,详细推导过程参见文献[11-12]。同时,采用人工应力法来避免拉伸不稳定性,并用粒子-粒子型接触算法来准确地处理接触界面,最终得到本文计算用的SPH方程的形式如下
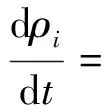
(1)
(2)
(3)
式中:i,j为粒子编号,N为粒子总数;r,z和θ分别为径向、轴向和周向坐标;t为时间,ρ为密度,η=2πrρ,m为质量,v为速度,σ为应力;W为三次样条光滑函数;Q为人工黏性,fnR为人工应力项,F为接触力。人工黏性Q按下式计算
(4)
式中:CL和CQ分别为线性和二次系数,分别取为0.5和1.0;c是声速;μij的计算表达式为
(5)
式中:dij表示粒子i和j间的距离,且
(6)
(7)
式中:h表示粒子的光滑长度。在人工应力项中,f按下式计算得到
(8)
式中:Δp表示局部粒子间距;而人工应力分量Rrr、Rzz和Rrz则按下式计算
(9)
其中
(10)
(11)
(12)

(13)
式中:Nc为与粒子i接触的粒子总数,Fnij和Fτij分别为法向和切向接触罚力。法向接触罚力的计算式为
(14)
式中:αp为罚力系数,Δt为时间步长,nij为粒子i和j的平均法向量,P为粒子i和j之间的穿透距离,其计算式为
(15)
其中
B=nij·xji,xji=xj-xi,
C=(dij)2-(Ri+Rj)2
(16)
式中:x=(r,z)表示位置矢量,Ri和Rj分别为粒子i和j的半径,Ri=Δpi/2,Rj=Δpj/2;平均法向量nij按下式确定
(17)
式中:ni和nj分别为粒子i和j的单位外法向量。切向接触罚力Fτij的计算式为
(18)

(19)
其中
Δvni=(Δvi·nij)nij
(20)
2 平头弹正侵彻钢板的SPH模型及其验证
图1给出了平头弹正侵彻单层和多层钢板的SPH模型。弹体长度为80 mm,直径为20 mm,质量为0.197 kg。弹体材料为Arne工具钢,采用双线性弹塑性材料模型,其模型参数见表1。靶板具有直径500 mm的圆形自由变形区域,其材料为Weldox 460 E钢。靶板材料采用Børvik等[13]提出的材料本构模型,模型参数见表2。弹体离散为19 551个粒子;靶板的粒子间距为0.2 mm,粒子数目随厚度变化而变化。模型采用固定粒子对靶板周边进行约束。固定粒子被赋予靶板粒子相同的材料性能并纳入靶板粒子的SPH近似计算,其位移始终置为0。对于单层板,固定粒子布置在靶板边缘粒子的上下方;对于多层板,固定粒子布置在靶板边缘粒子的外围。考虑到摩擦的影响,弹体与靶板和靶板各层间的摩擦因数均取为0.05[14]。
Børvik等[15]开展了平头弹侵彻不同厚度单层Weldox 460 E钢靶的实验,得到了不同侵彻速度下的弹体剩余速度。本文采用上述实验数据来验证SPH模型的合理性。图2比较了实验和SPH模拟得到的不同厚度单层靶的弹体剩余速度曲线。图中实线为最小二乘法拟合得到的弹体剩余速度曲线。拟合模型为

(a)单层板
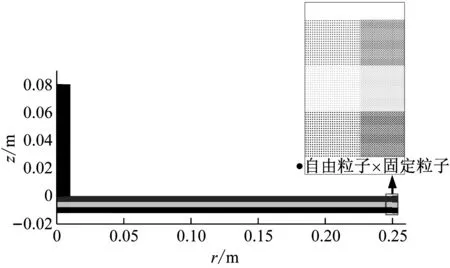
(b)多层板

表1 弹体的材料参数Tab.1 Material propeties for the projectile

表2 靶板的材料参数Tab.2 Material propeties for the target
(21)
式中:vi为侵彻速度,vr为剩余速度,vbl为弹道极限速度,a和p为模型参数。由图2可知,对于不同的靶板厚度,实验得到的弹体剩余速度和SPH模拟得到的剩余速度符合较好。表3比较了采用实验和SPH模拟得到的弹道极限速度。实验方法获得的弹道极限速度计算解取为弹体穿透钢板的最小侵彻速度和未穿透时的最大侵彻速度的均值,拟合解为采用上述拟合模型拟合实验数据得到的弹道极限速度。对于四种不同厚度的靶板,SPH模拟结果均与实验数据接近,最大误差为11.0%。综上所述,本文建立的SPH模型能够较好地预测Weldox 460 E钢靶的抗侵彻性能。

(a)6 mm

(b)8 mm
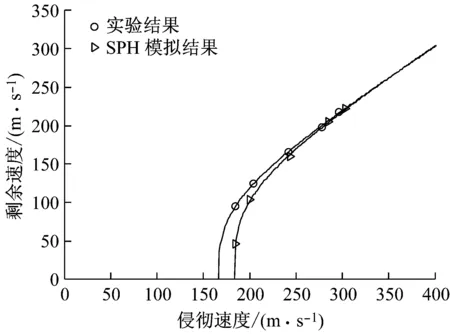
(c)10 mm

(d)12 mm

表3 弹道极限速度的对比Tab.3 Comparison of ballistic limit velocities
3 平头弹侵彻钢靶的数值模拟
本节将利用上述验证的SPH模型进一步开展平头弹侵彻单层和多层Weldox 460 E钢靶的数值模拟研究。对于单层靶,主要考虑厚度对靶板的抗侵彻性能的影响。对于多层靶,主要考虑层数、靶板总厚度和厚度组合对靶板的抗侵彻性能的影响。
3.1 厚度对单层板抗侵彻性能的影响
考虑6种不同的靶板厚度,厚度变化范围为2~12 mm,间隔为2 mm。图3给出了不同靶板厚度下弹体的剩余速度。可见,在相同的侵彻速度下,弹体剩余速度随着靶板厚度的增加而减小。同时,随着靶板厚度的增加,靶板的弹道极限速度越来越大,其抗侵彻性能随之提高。

图3 弹体侵彻不同厚度的单层靶时的剩余速度Fig.3 Residual velocity versus impact velocity for mono-layer targets with different thickness
图4给出了不同厚度的单层靶的弹道极限速度。可见,弹道极限速度随靶板厚度的增加而单调增加,且呈非线性增长趋势。弹道极限速度vbl与厚度T之间的关系可用以下经验公式较好地描述
vbl=b1Tb2
(22)
式中:b1和b2为常数。当vbl和T分别以m/s和m为单位时,通过最小二乘法拟合可以得到b1=3.09×103和b2=0.60。图4中的实线为由经验公式(22)得到的弹道极限速度曲线。

图4 不同厚度靶板的弹道极限速度Fig.4 Ballistic limit velocity versus target thickness
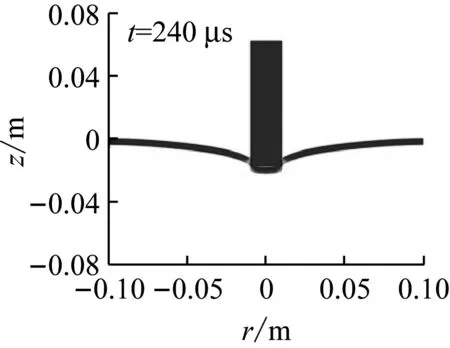
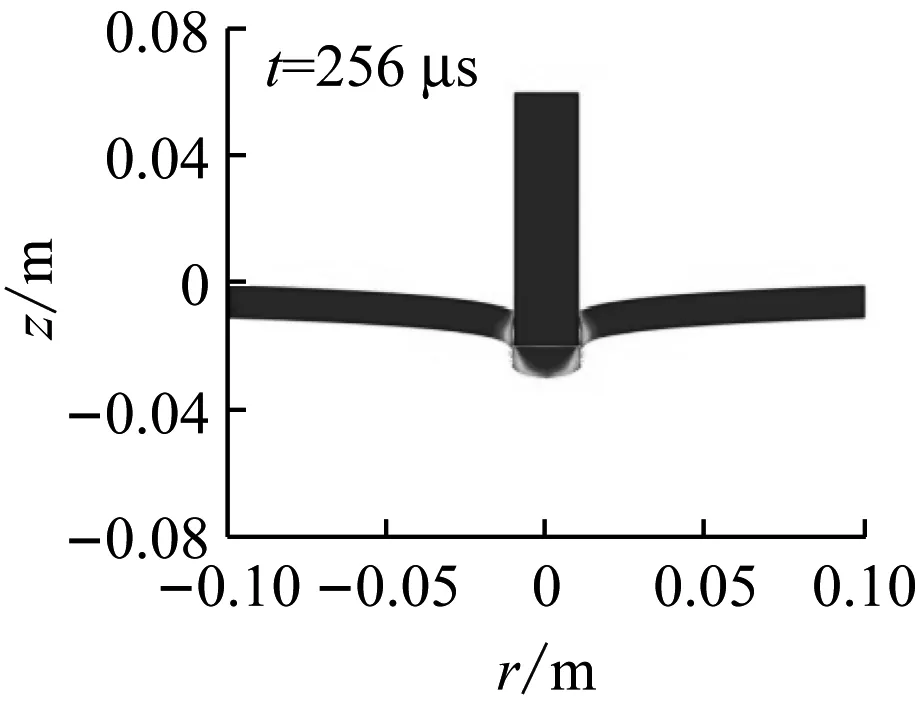
图5为弹体以接近弹道极限速度侵彻不同厚度单层靶的变形图。可见,随着靶板厚度的增大,靶板的抗弯刚度增加,靶板的整体变形范围和变形量逐渐变小,变形局部化更严重。另外,各种厚度的靶板在失效过程中,均形成了一个直径与弹体直径相近的圆柱形塞块。
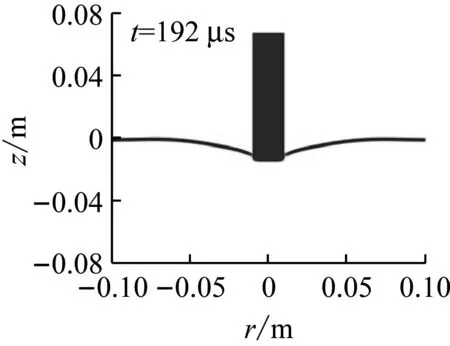
(a) 2 mm,vi=80 m/s
(b) 4 mm,vi=110 m/s

(c) 6 mm,vi=145.6 m/s

(d) 8 mm,vi=165.2 m/s
(e) 10 mm,vi=185 m/s

(f) 12 mm,vi=200.4 m/s
图5 平头弹以接近弹道极限速度侵彻不同厚度单层靶的变形
Fig.5 Deformations of mono-layer targets with different thickness under impact of blunt projectiles at impact velocities close to ballistic limits
3.2 层数对多层靶抗侵彻性能的影响
考虑(6 mm)2、(4 mm)3和(3 mm)4三种多层靶板。三种靶板的总厚度均为12 mm,层数分别为2,3,4,每种靶板各叠层厚度相等。图6给出了弹体侵彻不同层数的多层靶的剩余速度,并与相同厚度单层靶的结果进行了对比。由该图可见,层数对靶板抗侵彻性能的影响较复杂。在较高的侵彻速度下,弹体侵彻双层靶和三层靶的剩余速度高于侵彻单层靶的剩余速度,而在较低侵彻速度下出现相反的规律。另外,弹体侵彻四层靶的剩余速度在各种侵彻速度下都高于侵彻单层靶的剩余速度,但两者的差异随侵彻速度的降低而缩小。双层靶和三层靶的弹道极限速度分别为203.8 m/s和204.9 m/s,分别比单层靶的弹道极限速度高5.8%和6.3%。四层靶的弹道极限速度为192.0 m/s,略低于单层靶。
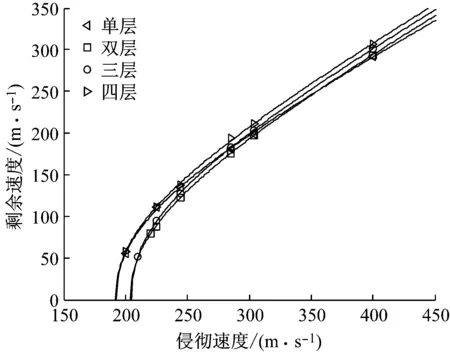
图6 多层靶弹体剩余速度Fig.6 Residual velocity for layered target
图7给出了平头弹以相同侵彻速度(vi=244.2 m/s)侵彻不同层数的靶板时弹体的速度历程曲线。可见,由于单层靶刚度较大,对弹体的抗力较大,因而弹体减速较快,但单层靶发生冲塞失效后,对靶板的抗力迅速消失,且弹体与形成的塞块间不发生碰撞,因此弹体减速时间短。而对于多层板,分层使得靶板刚度降低,对弹体抗力减少,因而弹体减速较慢。但是,由于弹体与靶板的前层接触作用时,靶板的后层被加速并发生变形,弹体与靶板后层间的相对速度变小、相互作用时间变长。另外,靶板前层失效产生的塞块在靶板后层的约束下与弹体产生碰撞,并在弹体推动下穿透靶板后层。这样,平头弹在侵彻多层靶时的减速时间较长且速度变化过程复杂。对于不同层数的多层靶,分层导致的靶体抗力减小程度和弹靶相互作用时间增长程度不同,从而其抗侵彻性能也就出现不同。

图7 弹体速度历程Fig.7 Velocity histories of the projectile
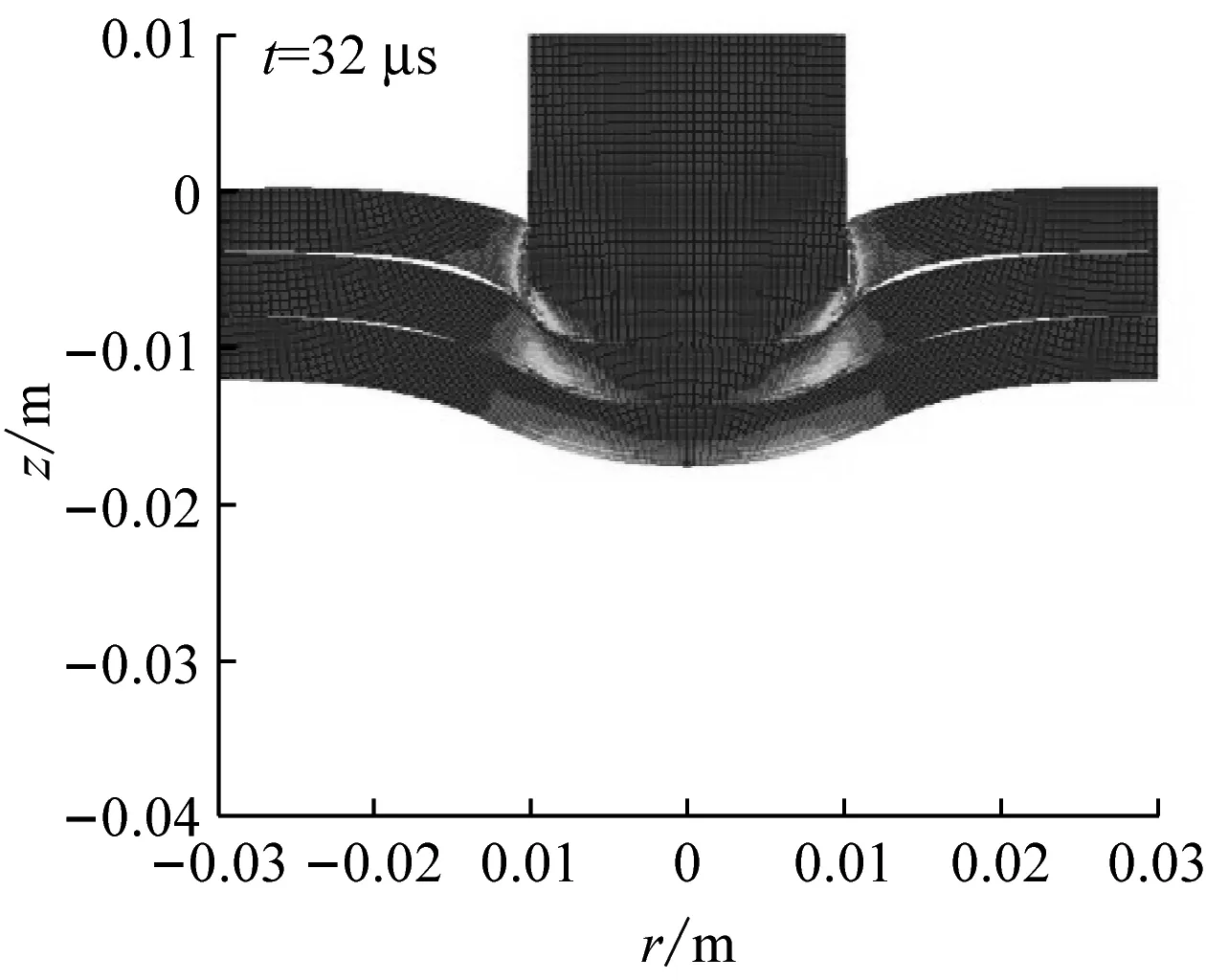
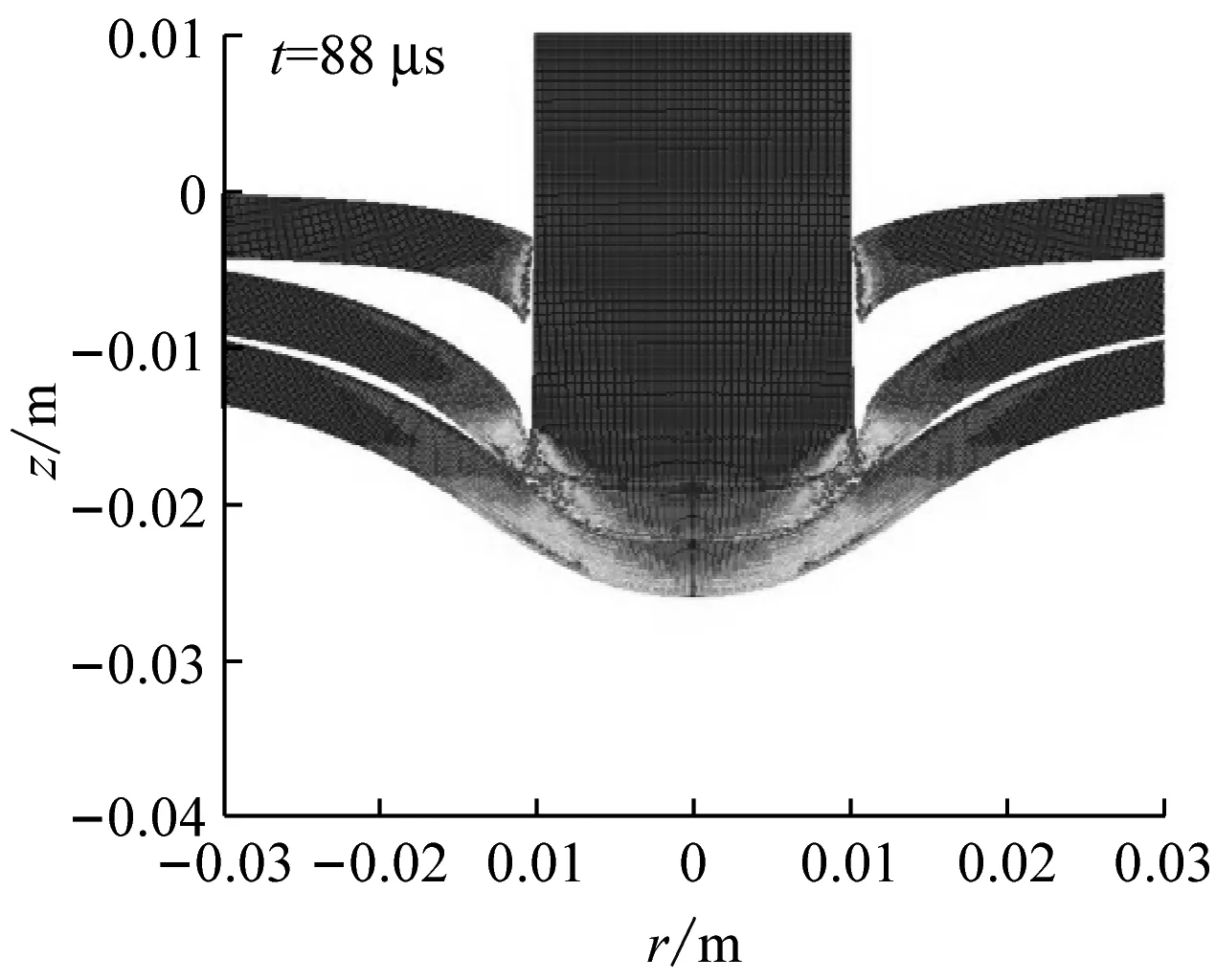
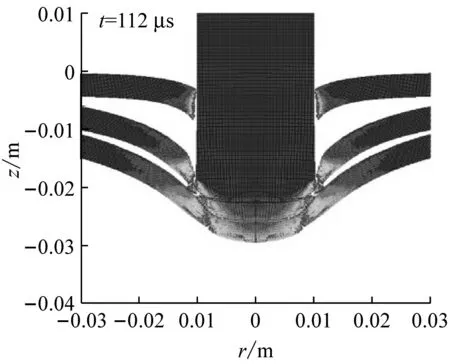
图8给出了相同侵彻速度(vi=244.2 m/s)下不同层数靶板的变形图。可见,沿侵彻方向越靠后的叠层,其弯曲变形越大。这主要是因为各叠层间存在接触相互作用力,而这个作用力阻碍前一叠层的变形、促进后一叠层的变形。另外,与单层靶的破坏形式相似,多层靶中每一叠层在侵彻过程中均会形成一个较大的塞块。各叠层的塞块形状存在一定的差异,形成的机制也有所不同。以三层靶为例,图9给出了三层靶在侵彻过程中不同时刻的变形图。可见,第一层靶主要是由于绝热剪切失效而形成塞块;第二层靶主要是受弹体、第一层靶板的塞块以及第三层靶板的共同挤压作用,发生较大压缩变形后而产生塞块;第三层靶受弹体和两个塞块的冲击作用,沿约45°方向发生破坏而形成塞块。叠层越靠后,对应的塞块直径越小。

(a)单层

(b)双层

(c)三层
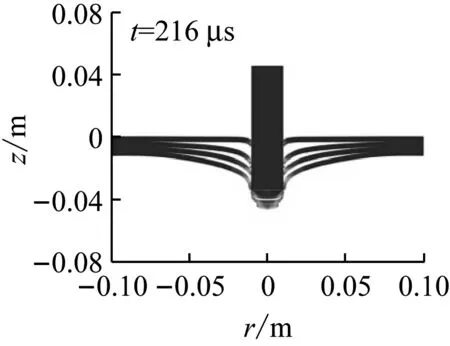
(d)四层
(a)
(b)
(c)
3.3 总厚度对双层靶板抗侵彻性能的影响
模拟了(2 mm)2、(4 mm)2和(6 mm)2三种不同总厚度的双层靶。图10给出了平头弹侵彻不同总厚度双层靶的剩余速度,并将其与对应厚度的单层靶的结果进行了对比。由图10可见,随着双层靶总厚度增大,弹体的剩余速度减小,靶板的弹道极限速度增大、抗侵彻性能提高。同时可见,在高侵彻速度下,弹体侵彻相同厚度的单、双层靶的剩余速度差异较小,而在低侵彻速度下,两者的差异相对较大。
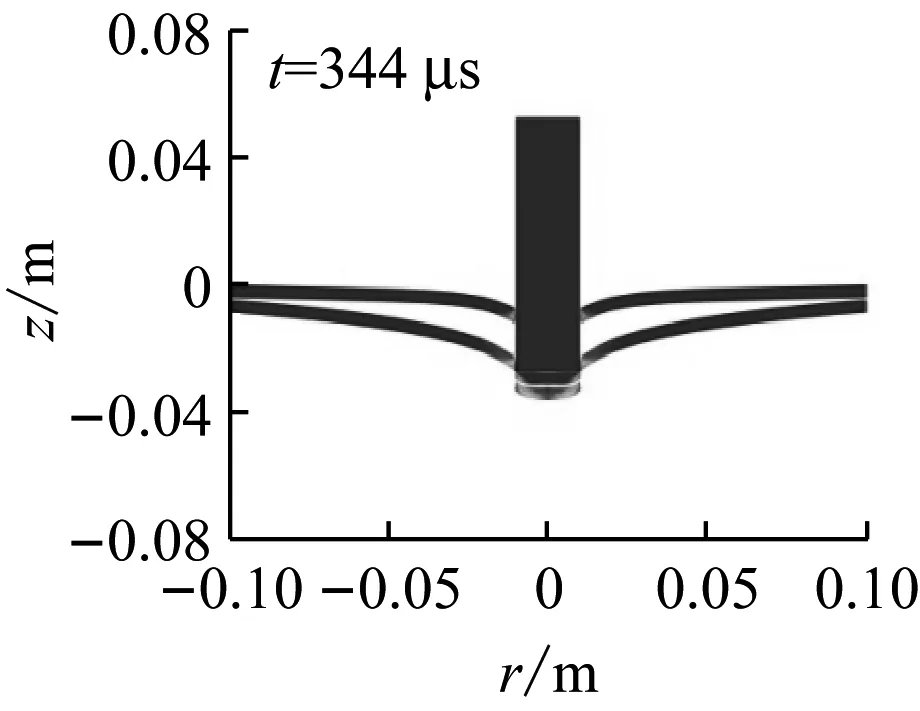
表4对比了不同总厚度的单、双层靶的弹道极限速度。由该表可见,相同厚度的单、双层靶的弹道极限速度都存在一定的差异,说明分层对靶板抗侵彻有一定影响。并且,总厚度不同,分层对靶板抗侵彻性能的影响规律也不同。当总厚度较薄(4 mm和8 mm)时,双层靶的抗侵彻性能低于等厚度的单层靶;而当总厚度较厚(12 mm)时,双层靶的抗侵彻性能高于等厚度的单层靶。图11给出了弹体以接近弹道极限速度侵彻两种不同总厚度双层靶的变形图。(6 mm)2双层靶的变形图见图8(b)。

图10 不同厚度靶板的弹体剩余速度Fig.10 Residual velocities of the projectile for targets with different target thickness
表4单、双层靶的弹道极限速度
Tab.4Ballisticlimitvelocitiesofmonolithicanddouble-layeredtargets

总厚度/mm层数靶厚配置弹道极限速度vbl/(m·s-1)相对差异/%4单层-99.84双层(2 mm)288.2-11.68单层-163.18双层(4 mm)2153.3-6.012单层-192.712双层(6 mm)2203.85.8

(a) 4 mm,vi=100 m/s
(b) 8 mm,vi=160 m/s
图11 平头弹以接近弹道极限速度侵彻不同总厚度双层靶的变形
Fig.11 Deformations of double-layered targets with different total thickness under impact of blunt projectiles at impact velocities close to ballistic limits
3.4 厚度组合对双层靶抗侵彻性能的影响
进一步模拟了平头弹侵彻四种不同叠层厚度组合的12 mm厚双层靶,即2 mm+10 mm靶、10 mm+2 mm靶、4 mm+8 mm靶和8 mm+4 mm靶,并结合前面已模拟的(6 mm)2双层靶,研究叠层厚度组合对双层靶抗侵彻性能的影响。图12给出了弹体侵彻不同厚度组合的靶板的剩余速度。由图12可知,各种厚度组合的12 mm厚双层靶的弹道极限速度都大于等厚度单层靶的弹道极限速。同时,厚度组合对双层靶的弹道极限速度影响较明显。薄板在前、厚板在后的双层靶的抗侵彻性能比薄板在后、厚板在前的好。2 mm+10 mm双层靶具有最高的弹道极限速度,而10 mm+2 mm双层靶的弹道极限速度最低,前者较后高约14.5%。图13给出了相同侵彻速度(vi=244.2 m/s)下不同厚度组合的双层靶的变形图。
4 平头弹侵彻多层钢靶的解析研究
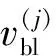

图12 不同厚度组合的双层靶的弹体剩余速度Fig.12 Residual velocities of the projectile for double-layered targets with different thickness configuration
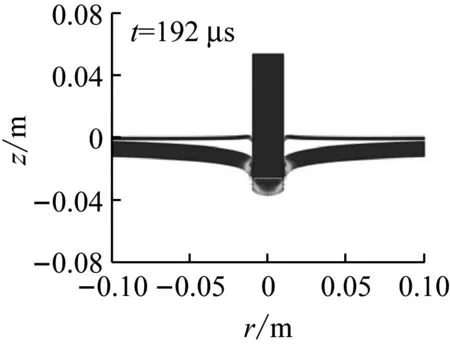
(a) 2 mm+10 mm

(b) 10 mm+2 mm

(c) 4 mm+8 mm
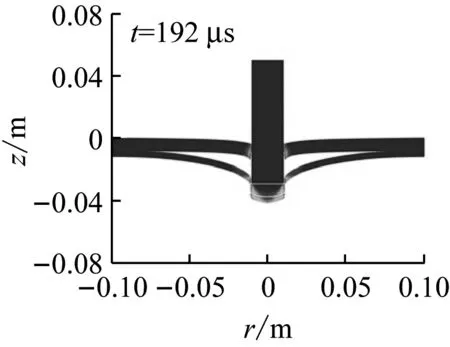
(d) 8 mm+4 mm
(23)
(24)
式中:vi和vr分别为多层靶的弹体侵彻速度和剩余速度。令式(24)中的vr=0,最终得到多层靶的弹道极限速度计算式为
(25)
其中
(26)
式中:T(j)为多层板的第j层的厚度。将前面得到的单层Weldox 460 E钢靶的弹道极限速度拟合公式(22)代入式(26),可得到函数G的表达式为
G(T)=(b1Tb2)2=9.55×106T1.20
(27)
表5对比了按式(27)计算得到多层靶的弹道极限速度和前面用SPH模拟得到的结果。可见,解析结果和SPH模拟结果比较接近,但存在一定的差异。对于大部分多层靶来说,解析方法预测的弹道极限速度均小于相应的SPH模拟结果。其主要原因是解析方法忽略了多层靶中各层间的接触作用,且没有考虑靶体中形成的塞块对侵彻过程的影响,而SPH模拟综合考虑了这些因素的影响。同时,由表5可知,解析方法不能反映厚度组合对弹道极限速度的影响。如:对于4 mm+8 mm双层靶和8 mm+4 mm双层靶,解析方法给出了相同的弹道极限速度。定量地来看,解析结果和SPH模拟结果的相对误差基本都在10%以内,仅有1种情况超出该范围,达到19.1%。这说明应用该解析方法来预测多层Weldox 460 E钢靶抵抗平头弹侵彻的性能具有较高的可信度。
表5不同方法计算的弹道极限对比
Tab.5Comaprisonbetweenballisticlimitvelocitiespredictedbydifferentmethods

总厚度/mm层数靶厚配置vbl/(m·s-1)SPH模拟解析结果相对误差/%4单层-99.8--4双层(2 mm)288.2105.0-19.18单层-163.1--8双层(4 mm)2153.3159.1-3.412单层-192.7--12双层(6 mm)2203.9203.00.412双层2 mm+10 mm225.6208.67.512双层10 mm+2 mm197.1208.6-5.812双层4 mm+8 mm223.3204.38.512双层8 mm+4 mm212.6204.33.912三层(4 mm)3204.9194.94.912四层(3 mm)4192189.41.4
5 结 论
本文采用SPH方法和解析方法研究了平头弹体正侵彻Welox 460 E钢靶过程,得到如下主要结论:
(1)对于单层靶,靶板的抗侵彻性能随靶板厚度的增加而增加,靶板弹道极限速度与厚度之间的关系可以用经验公式vb1=3.09×103T0.60来描述。
(2)对于总厚度为12 mm的多层靶,层数为2和3的多层靶相对等厚度的单层靶可以提高弹道极限速度,而层数为 4的多层板的弹道极限速度略低于等厚度的单层靶的弹道极限速度。
(3)对于不同总厚度的双层靶(靶中两层板的厚度一致),靶板的抗侵彻性能与靶板总厚度成正比。当总厚度较薄时,双层靶的抗侵彻性能低于等厚度的单层靶;当总厚度较厚时,双层靶的抗侵彻性能高于等厚度的单层靶。
(4)对于不同厚度组合的12 mm厚双层靶,各种厚度组合的双层靶的弹道极限速度都大于等厚度单层靶的弹道极限速。同时,厚度组合对双层靶的弹道极限速度影响较明显。薄板在前、厚板在后的双层靶的抗侵彻性能比薄板在后、厚板在前的好。
(5)解析方法与SPH方法得到的多层靶弹道极限速度比较接近,相对误差基本都在10%以内(仅有1种情况超出,误差为19.1%),但解析方法不能反映厚度组合对靶板弹道极限速度的影响。
