基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法

2018-10-20秦仙蓉孙远韬

振动与冲击 2018年19期

李恒，张氢，秦仙蓉，孙远韬

(同济大学机械与能源工程学院，上海 201804)

滚动轴承是大多数机械传动装置的关键性零件，同时又极易损坏，若发生故障，甚至对整个机械设备造成严重破坏。由于从机械设备现场采集到的轴承振动信号，往往具有非平稳的特点，且噪声干扰严重，给故障模式识别带来了巨大的困难。近年来，随着监测的设备群规模变大，每个装备需要的测点增多，每个测点的采样频率高，从开始服役到寿命终止的数据收集历时长，致使机械设备故障诊断领域也进入了“大数据”时代[1]。如何利用“大数据”来提高强噪声、非平稳信号的故障诊断精度，将成为今后的研究热点。

目前，针对强噪声和非平稳信号的轴承故障诊断，主要集中于特征提取方法的研究，希望找到能反映轴承故障模式，并对工况和噪声不敏感的特征。张小龙等[2]提出通过ITD-形态滤波滤除高频噪声信号后，用Teager能量谱提取有效故障特征的方法；钱林等[3]提出了变分模态分解(VMD)和自适应形态学滤波结合的方法，对故障信号进行降噪处理后提取故障特征频率；Unal等[4]利用Hibert-Huang变换分析滚动轴承振动信号，并通过傅里叶变换(FFT)提取故障特征。上述方法存在两个主要问题：①人工提取对噪声和工况不敏感的故障特征较为困难，且需要一定的先验知识；②将故障诊断分为信号预处理、特征提取和故障分类三个孤立的阶段，破坏了各个阶段的耦合关系，并造成了一部分故障信息的损失。因此，将预处理、特征提取和特征分类统一到一个框架下的端到端的故障诊断方式逐渐成为研究热点。目前，部分学者提出基于深度学习的端到端的故障诊断方法，不仅能够自适应的提取故障特征，而且能直接处理原始的故障信号。其中，Tamilselvan等[5]提出了一种基于深度置信网络(DBN)的故障诊断方法，验证了深度学习方法在故障模式识别方面的优势及可行性。

卷积神经网络(Convolution Neural Network，CNN)是一种有监督的深度学习算法，被广泛的应用于模式识别领域。魏东等[6]提出了基于CNN的输电线路内外故障模式的识别方法。CNN不同于其他深度学习算法的三大突出特点：局部感受野、权值共享以及池化。不仅降低了网络的复杂度，也减少了过拟合的风险，使得构建处理海量数据的深度学习框架成为可能。

Lu等[7]将CNN应用到滚动轴承的故障诊断中去，并验证了该方法在噪声环境下了鲁棒性。虽然在诊断结果上有一定的提高，但是存在着两个主要问题：①以时间序列重构的二维矩阵作为卷积神经网络的输入，丢失了故障信号的频率信息；②样本量少且CNN模型简单，没有体现CNN在处理大数据方面的优势。因此，本文提出了一种短时傅里叶变换(Short-time Fourier Transform,STFT)和CNN相结合的故障诊断方法，同时考虑了时域和频域信息，并利用CNN对故障特征进行的自适应提取，实现端到端的故障诊断。最后实验验证了CNN在处理“大数据”方面的优势，以及针对强噪声非平稳信号的鲁棒性。

1 短时傅里叶变换

短时傅里叶变换是针对时变、非平稳信号的一种联合时频分析方法。能将一维的故障振动信号变换成适应于CNN处理的二维矩阵：一种包含时域和频域信息的特征谱。

1.1 短时傅里叶变换的定义

STFT的基本思想是采用固定长度的窗函数对时域信号进行截取，并对截取得到的信号进行傅里叶变换，得到时刻t附近很小时间段上的局部频谱。通过窗函数在整个时间轴上的平移，最终变换得到每一时间段上局部频谱的集合，因此，STFT是关于时间和频率的二维函数。基本运算公式如下

(1)

式中:f(t)为时域信号；g(t-τ)为中心位于τ时刻的时间窗口。由此可以看出，STFT就是将信号f(t)乘以一个以τ为中心的窗函数g(t-τ)所做的傅里叶变换。

1.2 参数选择

对于STFT，影响其变换效果的因素有两个：窗函数类型和窗的宽度。选取好的窗函数能有效减少频谱泄露和谱间干扰[8]，而窗的宽度则影响着时域和频域的相对分辨率：窗宽则频率分辨率高；窗窄则时间分辨率高。因而需要根据特定信号的特征来合理选择窗函数宽度。时域和频域的分辨率可由下列公式计算得到

(2)

(3)

其中T和F分别表示时频谱图的时间和频率分辨率，[·]表示向下取整运算。Nx是参与STFT的样本长度，Nw是窗口宽度，No是窗口重叠宽度，Nf是参与傅里叶变换的点数，一般取Nf等于Nx。根据图像分辨率的定义，将时频谱的分辨率P定义为

P=T×F

(4)

P值大小决定了时频谱所包含的信息量，这些信息既包括有用的故障信息，也包含噪声干扰。因此合理的T和F，能够使故障信号显著，噪声干扰减少。

在轴承故障诊断实践中，故障特征频率是一种重要的参考指标。针对滚动轴承的振动信号，可以以故障特征频率的一倍频为依据选择样本长度，以二倍频为依据选择STFT的窗口宽度。滚动轴承的故障频率可以由下列公式计算得到

(5)

(6)

(7)

式中:fBPI、fBPO和fBS分别为滚动体过内圈频率、滚动体过外圈频率和滚动体自转频率;fH=n/60为内圈旋转频率;n为转速;d和D分别为滚动体和节圆直径;Z为滚子数目;α为接触角度。

2 卷积神经网络

卷积神经神经网络CNN是一种前馈神经网络，近年来在图像识别和目标检测方面有着出色的表现，能很好的处理过拟合问题，使更大规模的深度学习得以实现[9]。自从Lecun等[10]提出LeNet-5之后，卷积神经网络的基本结构就被确定下来，主要由卷积层、池化层和全连接层组成,如图1所示。

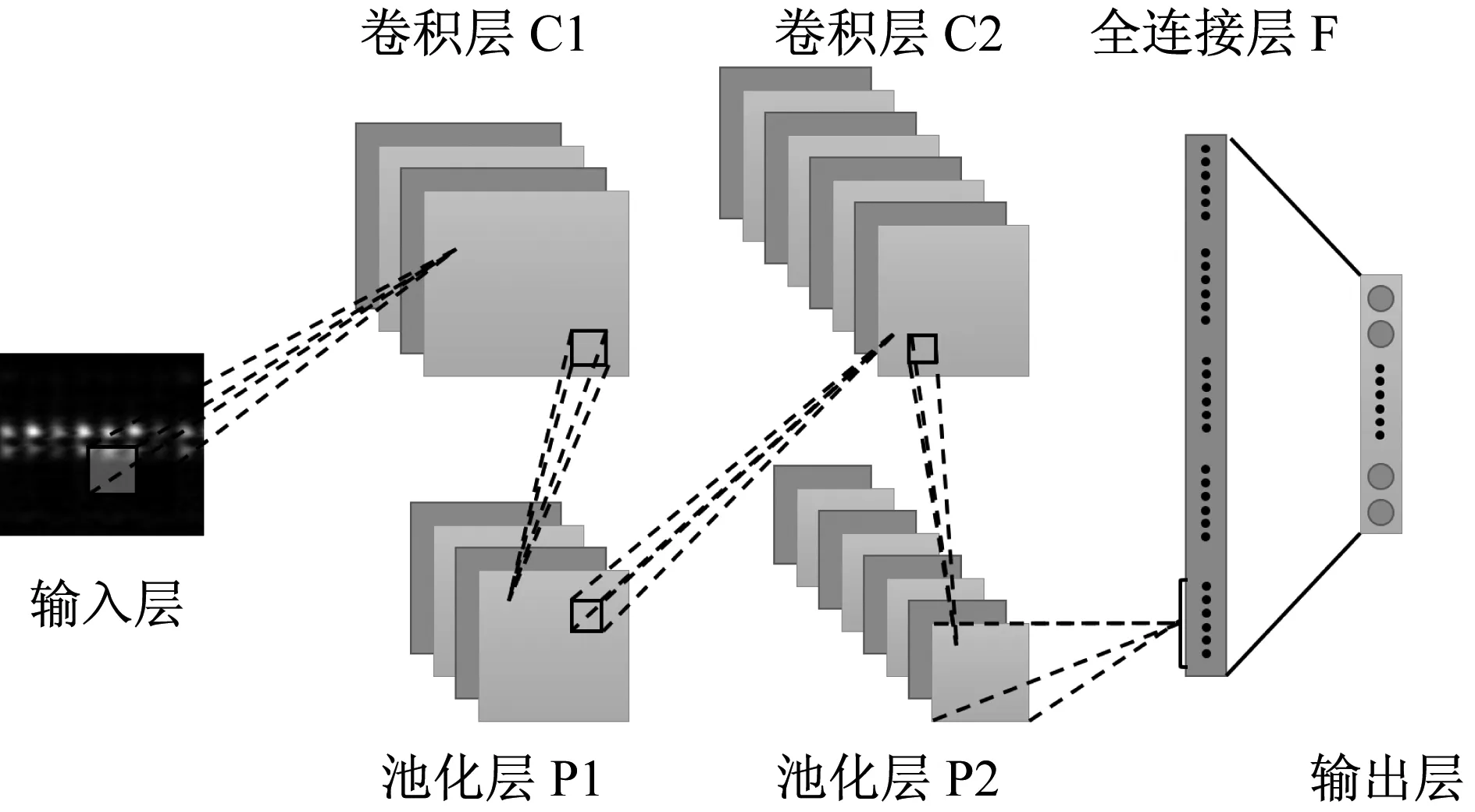
图1 卷积神经网络结构Fig.1 Structure of convolution neural network

在本文中CNN的输入为时频谱，经过卷积层、池化层和全连接层后，输出为故障类型的类标。CNN的学习过程主要分为前向传播过程和反向参数更新过程。

2.1 前向传播阶段

卷积神经网络的前向传播过程主要为三个部分：卷积层、池化层和全连接层。

2.1.1 卷积层

在卷积层上，用多个卷积核与输入图像进行卷积，加上偏置后通过一个激活函数就可以得到一系列特征图[11]，卷积过程数学表达式为

(8)

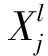
f(x)=max(0,lg(1+ex))

(9)

2.1.2 池化层

池化层常接在卷积层后面，对特征图进行降维，同时在一定程度上保持特征尺度的不变性。常用的池化方法有：最大值池化(Max Pooling)、平均值池化(Mean Pooling)、随机池化(Stochastic Pooling)等。池化层一般只进行降维操作，没有参数，不需要进行权值更新。

在池化层上，对卷积层输出的特征图在每个不重叠的大小为n×n区域进行池化操作，选取每个区域上的最大值或者平均值，最终使输出图像在两个维度上都缩小了的n倍。

2.1.3 全连接层

输入图像经过多个卷积层和池化层的交替传播之后，依靠全连接层网络针对提取的特征进行分类。在全连接层上，输入是所有特征图展开的一维特征向量经加权求和并通过激活函数后得到的

yk=f(wkxk-1+bk)

(10)

式中：k为网络层的序号;yk为全连接层的输出;xk-1是展开的一维特征向量;wk为权重系数;bk为偏置项。激活函数f(·)常使用Softmax，是一种适用于分类任务的激活函数。

2.2 反向参数更新

对于一个具体的分类任务，CNN的训练目标是最小化网络的损失函数，因此选择一个合适的损失函数十分重要。常见的损失函数有均方误差函数、交叉熵函数、负对数似然函数等[13]，本文选用效果较好的交叉熵作为损失函数，表达式如下

(11)

式中：n为该类故障的样本数;t为预测值;y为真实值。在训练过程中，最小化损失函数的方法是梯度下降法。通过对式(11)求一阶偏导数，可以逐层更新卷积神经网络的可学习参数(w和b)

(12)

(13)

式中：w′和b′为更新后的权重和偏置;w和b为现有的权重和偏置;η为学习速率参数，用来控制权值更新的步长。η太大，会使网络陷入局部最优；η过小，则会增加网络的训练时间。

2.3 基于CNN的故障诊断流程

基于CNN的故障诊断方法能够将信号预处理、故障特征提取和故障模式分类融合到一起，实现故障特征自适应提取及智能诊断的具体流程,如图2所示。采集的振动信号经STFT后，被分成训练集和测试集。首先将训练集输入到CNN中进行参数学习，并用梯度下降法不断更新权重(w)和偏置(b)。然后将训练好的参数应用于测试集，得到故障诊断结果。

3 试验验证

本节将针对滚动轴承实测的振动信号，验证所提出方法的可行性和有效性，并讨论该方法在变转速工况和强噪声环境下的鲁棒性。

3.1 数据集描述

数据集1 美国凯斯西储大学所公开的轴承试验数据。试验用电动机转速为1 792 r/min，采样频率为12 kHz。本文将驱动端轴承座的振动信号分为10种故障模式，依次为正常状态以及内圈、外圈和滚动体分别在损伤斑点为0.18 mm、0.36 mm、0.54 mm三种直径下的故障模式。每类故障的振动信号被分为400个样本，共建立了一个具有4 000个样本的故障数据集。对每种故障类标采用“独热(one-hot)”的编码方式，即设置一个向量，其维数与故障类别数相同，除了某一位数字是1以外其余各维数字都是0。例如将正常轴承信号的类标设置为0，则可以编码成([1,0,0,0,0,0,0,0,0,0])。

图2 基于CNN的故障诊断流程图Fig.2 Flowchart of the CNN-based method for fault diagnosis

滚动轴承型号为SKF6205，参数见表1。由式(5)～式(7)计算出故障特征频率,如表2所示。根据一倍频和二倍频所对应的特征周期确定样本长度为0.085 s(1 024个采样点)，STFT的窗口宽度为0.01 s(128个采样点)。

表1 滚动轴承SKF6205参数Tab.1 Parameters of the SKF6205

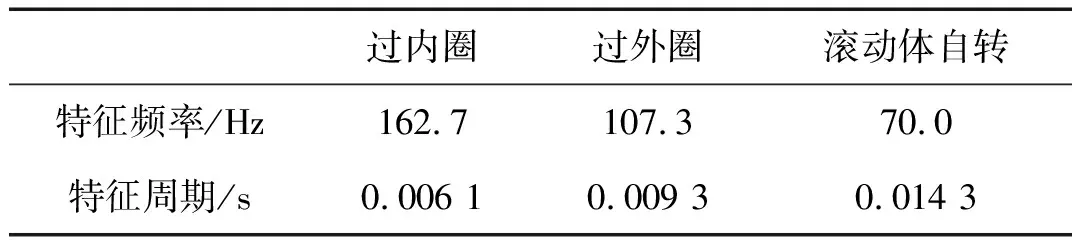
表2 SKF6205故障特征频率Tab.2 Fault frequencies of the SKF6205

STFT采用64点和114点两种不同的重叠点数，得到两种不同分辨率的时频谱。由式(2)～式(4)可以计算得到分辨率分别为65×15和65×65，将这两种时频谱都输入到CNN进行故障识别，以正确率为指标选择其一作为输入。图3为内圈和外圈故障情况下，不同分辨率的时频谱。

数据集2 由QPZZ-II旋转机械故障试验平台(见图4)采集到的轴承实验数据。实验使用东华测试的便携式数据采集分析系统(DH5901)采集轴承座处的振动信号，采样频率为12.8 kHz。分别测试轴承在转速600 r/min、900 r/min、1 200 r/min的运行状态，并设置一个600～1 200 r/min的升速过程模拟变转速非平稳运行工况。实验用轴承型号为N205E和NU205E，分别为外圈可拆卸式和内圈可拆卸式，滚子数目为13个，其他参数与SKF6025相同，如表1所示。计算转速900 r/min情况下的特征频率,如表3所示。试验前用线切割加工的方式，分别在内圈、外圈和滚动体上加工出不同损伤程度的凹槽，如图5所示。

图3 不同分辨率下的故障时频谱Fig.3 Time-frequency spectrums of faults at different resolutions

图4 QPZZ-II旋转机械故障试验平台Fig.4 QPZZ-II rotating machinery test rig

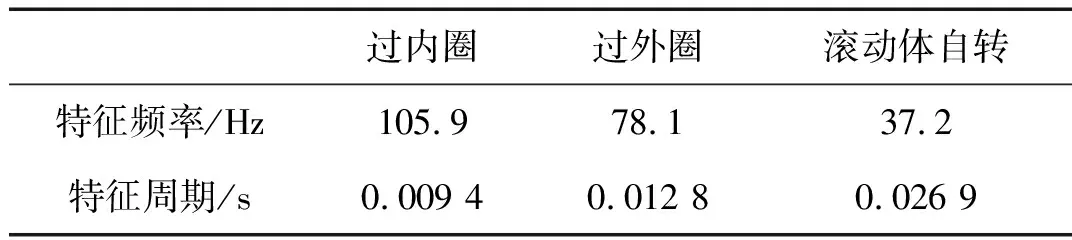
表3 N205E/NU205E故障特征频率Tab.3 Fault frequencies of the N205E/NU205E

图5 滚动轴承内圈和滚动体的故障形式Fig.5 The faults of inner ring and rolling element

试验安排了9种模式的故障：正常、内圈和外圈轻-中-重三种程度的故障、滚动体轻度和重度故障。在每类故障中选取400个样本，建立一个具有3 600个样本的数据集。同样可以根据故障特征频率确定样本长度为1 024个采样点，STFT的窗口宽度为128的采样点。

3.2 卷积神经网络模型建立

目前，对如何确定CNN的结构尚没有明确的方法，很大程度上取决于经验。卷积层中卷积核的大小和数目、池化层的大小及层数、全连接层的神经元数目等参数的选择都影响着CNN的识别效果。本文在LetNet-5基础上，改变一些网络参数，从中寻找适应于滚动轴承故障诊断的CNN模型。其参数如表4所示，其中C表示卷积层，P表示池化层，F表示全连接层。

表4 LetNet-5模型的参数Tab.4 The parameters of LetNet-5

将卷积层C1和C2的卷积层数目、卷积核大小(C1和C2相同)以及全连接层F的神经元数目作为变量，并定义取值范围为

{′C1′:2,4,8,16,32,64;

′C2′:2,4,8,16,32,64;

′F′:128，256,512,1024,2 048;

′卷积核大小′:2×2,4×4,5×5,6×6;}

这些参数可以组合成576种CNN模型，以遍历的方式，同时考虑识别正确率和训练时间两个指标，在这些组合中确定最优的网络结构。在实验过程中，发现去掉LeNet-5模型中的C3层，并在输入层和卷积层C1之间增加一个池化层P0之后，能在取得高故障识别正确率的同时大大减少训练时间。结果如表5所示，实验平台为windows10+Python，CPU采用英特尔Core i5-6500。

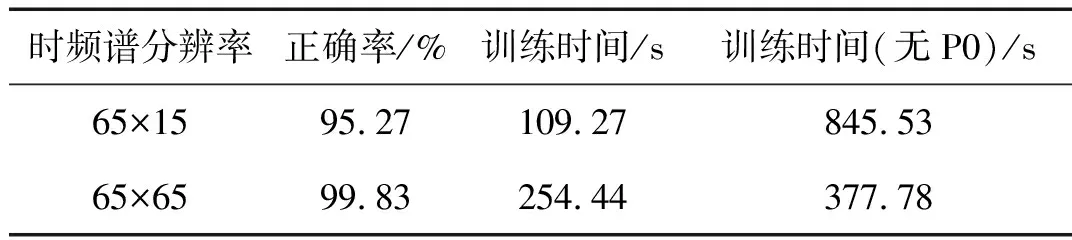
表5 最优网络结构的识别结果Tab.5 Fault identification results of optimal network structure

取正确率最高的情况，确定输入为65×65的时频谱，最优网络结构,如表6所示。为一个8层的CNN模型“In-P0-C1-P1-C2-P2-F-Out”，卷积核大小为4×4。可将时频谱分辨率修改为64×64(消去一行一列)，都圆整成2的倍数形式，能减少一定训练时间，且对最后的正确率影响不大。

表6 卷积神经网络的结构Tab.6 The structure of convolution neural network

确定输入和网络结构之后，本文分别使用不同的输入数据格式和网络结构，如表7所示。设计了两组对比试验：①验证输入为二维图谱的方法比输入为一维时间序列具有更好的故障识别效果。对比实验采用“In-H1-H2-F-Out”的5层BP神经网络结构直接对一维时间序列进行训练，这里的H1和H2代表隐层。时间序列样本长度取1 024个采样点;②验证以STFT后的时频谱作为CNN的输入比Lu等直接对时间序列重构得到的时间图作为输入具有更高的故障识别正确率。时间图是将时间序列按行重新排列得到的二维矩阵，本文将1 024个采样点重构成32×32的时间图作为输入。其使用的7层CNN结构为：“In-C1-P1-C2-P2-F-Out”。

表7 输入数据格式设置Tab.7 The formats setting of the input data

对于“3.1”节所建立的数据集，同样采用遍历的方法，得到表7中所设置的三种网络结构，能很好的兼顾计算时间以及训练集的收敛速度。

在数据集1中，有10类故障，每类故障有400个样本，总共4 000个样本，分成3 200个样本的训练集和800个样本的测试集。同时在数据集2中选取900 r/min转速下的9类故障信号组成具有3 600个样本的数据集，并分成3 000个样本的训练集和600个样本的测试集。训练过程采用“抓包”的形式，即每步从训练集中抓取一个子集输入网络做进行训练，并在每次训练之后将得到的参数应用于测试集，将识别出的故障类标与正确类标比较，并按下式计算每个子集的正确率

(14)

式中:ui为子集中第i个样本的识别结果，若识别正确，ui等于1，识别错误，ui等于0；N为子集样本数，本文中为50。

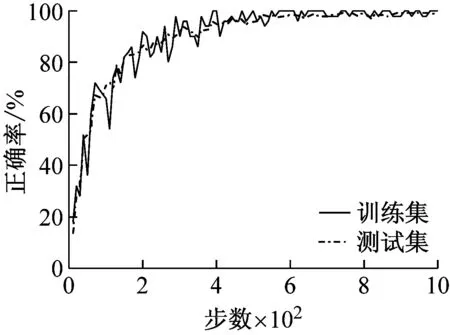
图6表示采用两个数据集进行轴承故障诊断模拟实验的结果。每幅图的横坐标代表训练步数，纵坐标代表故障识别正确率。由图6(a)和图6(d)可以输入为时间序列虽然在训练集上都达到了100%的故障识别正确率，但测试集的正确率仅为60%和30%。图6(b)和图6(e)所示输入为时间图，故障识别正确率有了一定的提高，达到了90%和60%，且训练集和测试集的差距减少。如图6(c)和图6(f)所示，将时间图替换成STFT后的时频谱，则不仅在训练集和测试集上都取得了非常高的识别精度，而且收敛速度也得到了明显的提升。

输入为时间序列

(a)

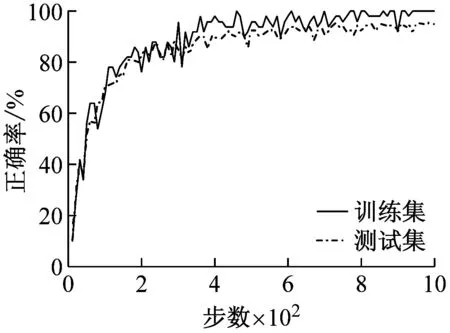
(b)

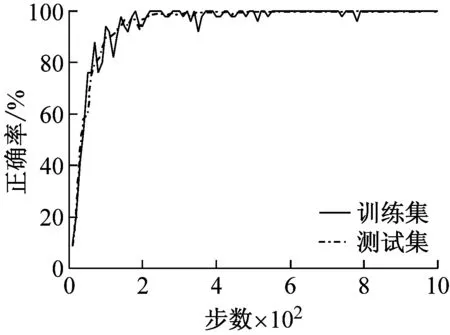
(c)

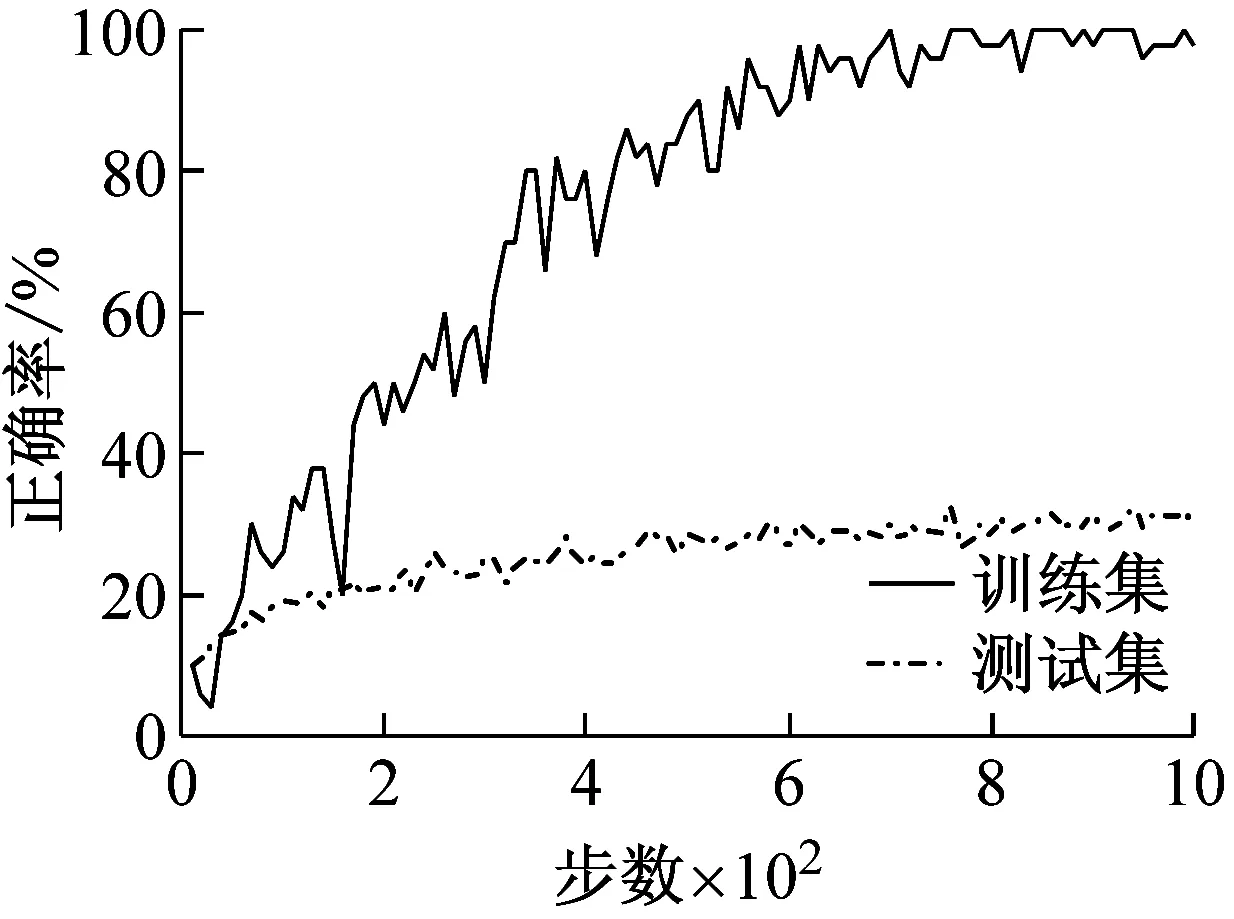
(d)

(e)

(f)

表8给出了三种输入格式下，CNN所需的训练时间以及对单个样本进行识别的时间。在实际的故障诊断中，由于CNN的网络参数是事先训练好的，所以故障诊断的时间效率应该用识别时间作为评价标准。从表8可知,虽然三种输入形式在训练时间上存在较大差距，但是在对单个样本的识别时间上，差距不大，都在1 s左右。

表8 三种形式输入的时间效率Tab.8 The time efficiency of the three forms of input

从实验结果中可以看出，输入为时间序列和时间图时，在数据集1上取得的效果要优于数据集2，这是由于在QPZZ-II旋转机械故障试验平台进行实验时，轴承装配间隙比较大，噪声干扰严重，振动信号呈非平稳性。而使用STFT与CNN结合的识别时频图的方法在两个数据集上都取得了很高的故障识别正确率，说明此方法具有一定的鲁棒性，能够处理非平稳和强噪声干扰的信号。

3.3 方法鲁棒性验证

将时频谱输入CNN经训练后得到的网络参数，直接用于鲁棒性验证试验。在数据集2中，选取变转速运行时的振动信号样本一共1 000个样本，分成10组，进行故障识别，并与“3.2”节中恒定转速900 r/min下的故障识别正确率进行对比，结果如图7所示。

由图7可知，对于恒定转速900 r/min的轴承振动信号数据，“3.2”节中训练得到的卷积神经网络参数能很好的识别出故障类别，但在变转速情况下的故障识别正确率却差了很多，这是因为所使用的网络参数是在900 r/min的恒定转速数据集上训练得到的，CNN提取的特征不能很好的排除转速变化的影响。因此，希望能通过构造一个更加庞大的数据集，包含各种转速下的故障信息，并输入到CNN中进行学习，得到对变转速工况不敏感的故障特征。试验采用包括600 r/min，900 r/min和1 200 r/min转速下的所有的故障信号，建立了具有10 800个样本的数据集。经训练得到网络参数，应用在测试集上。得出的识别结果,如图8所示。

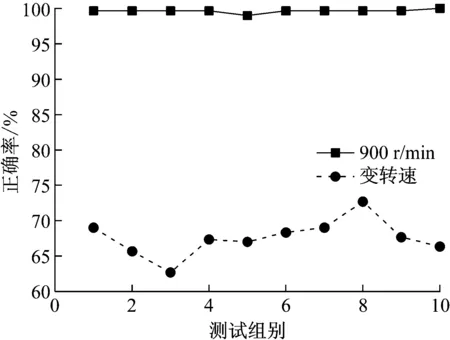
图7 变转速与恒定转速识别结果对比Fig.7 Results of fault recognition between variable speed and constant speed

图8 大数据集下变转速与恒定转速识别结果对比Fig.8 Comparison of variable speed and constant speed in bigger dataset

使用一个包含各种转速的故障数据集进行训练得到的网络参数，能很好的识别出变转速和恒定转速情况下的故障模式。说明CNN是一种基于数据驱动的故障诊断方法，数据量越大，故障模式越完整，诊断效果越好。同样，在解决噪声干扰时，也可以通过增加数据量的方式提高模型的鲁棒性。图9为变转速工况下正常和外圈重度故障的振动数据分别加上10 dB和20 dB的高斯噪声后的时域图像。使用与图8一样的网络参数进行故障识别。得到的结果,如图10所示。

从图10可知，在识别受噪声干扰的故障信号时，正确率明显下降。同样使用增加数据的方法，构造一个包含噪声干扰在内的数据集，输入到CNN中进行训练，提取出对噪声不敏感的故障特征，进行故障识别，结果如图11所示。

表9总结了不同数据格式在各种环境下的故障识别正确率。可以看出，如果采集到的轴承振动信号能包含各种工况、各种环境下的各类故障模式，那么基于STFT和CNN的故障诊断方法，能够取得非常好的故障识别率。这就建立了鲁棒性和数据量之间的关系，说明此种方法是一种适应于处理“大数据”的故障诊断方法。

正常外圈重度故障

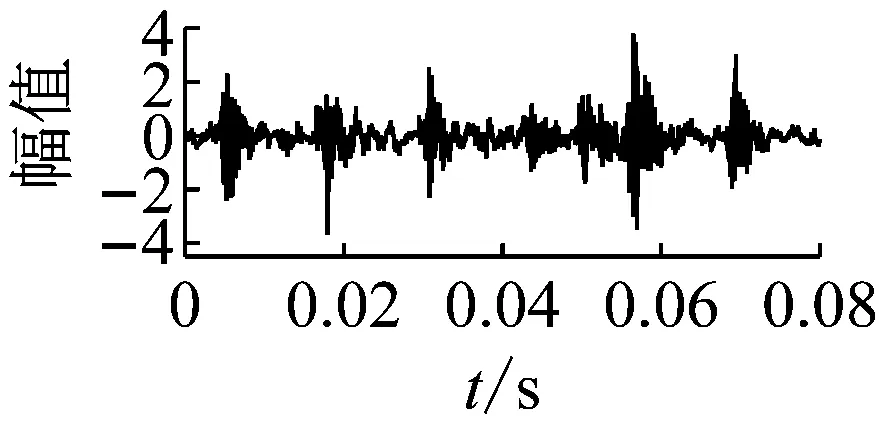
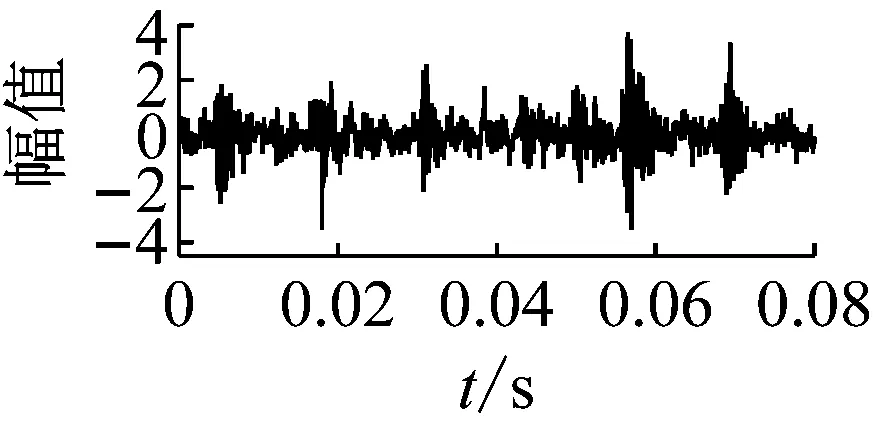
图9 不同噪声下的振动信号时域图像Fig.9 Time domain images of vibration signal with different noises

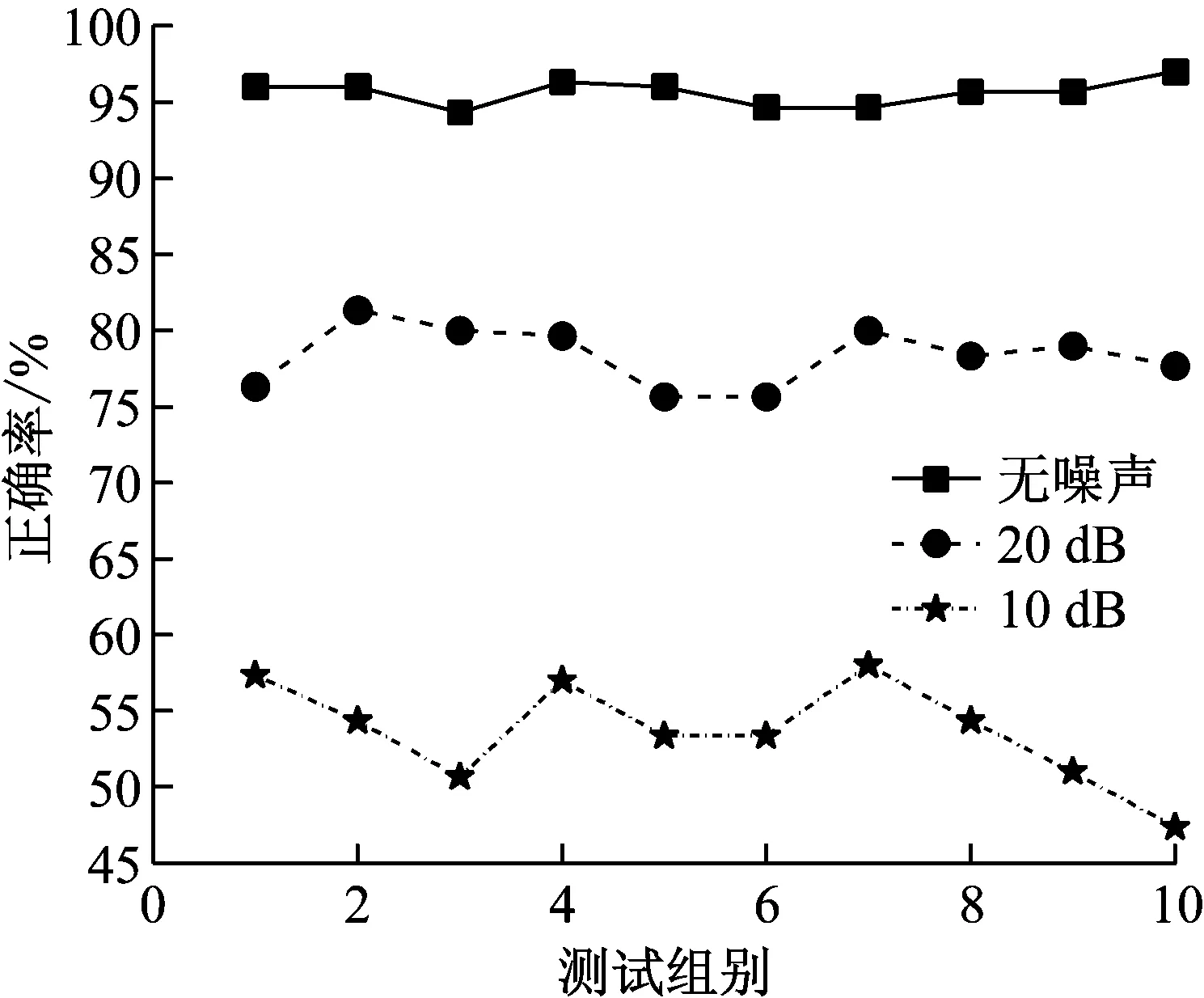
图10 不同噪声下的故障识别结果Fig.10 Results of fault recognition under noises

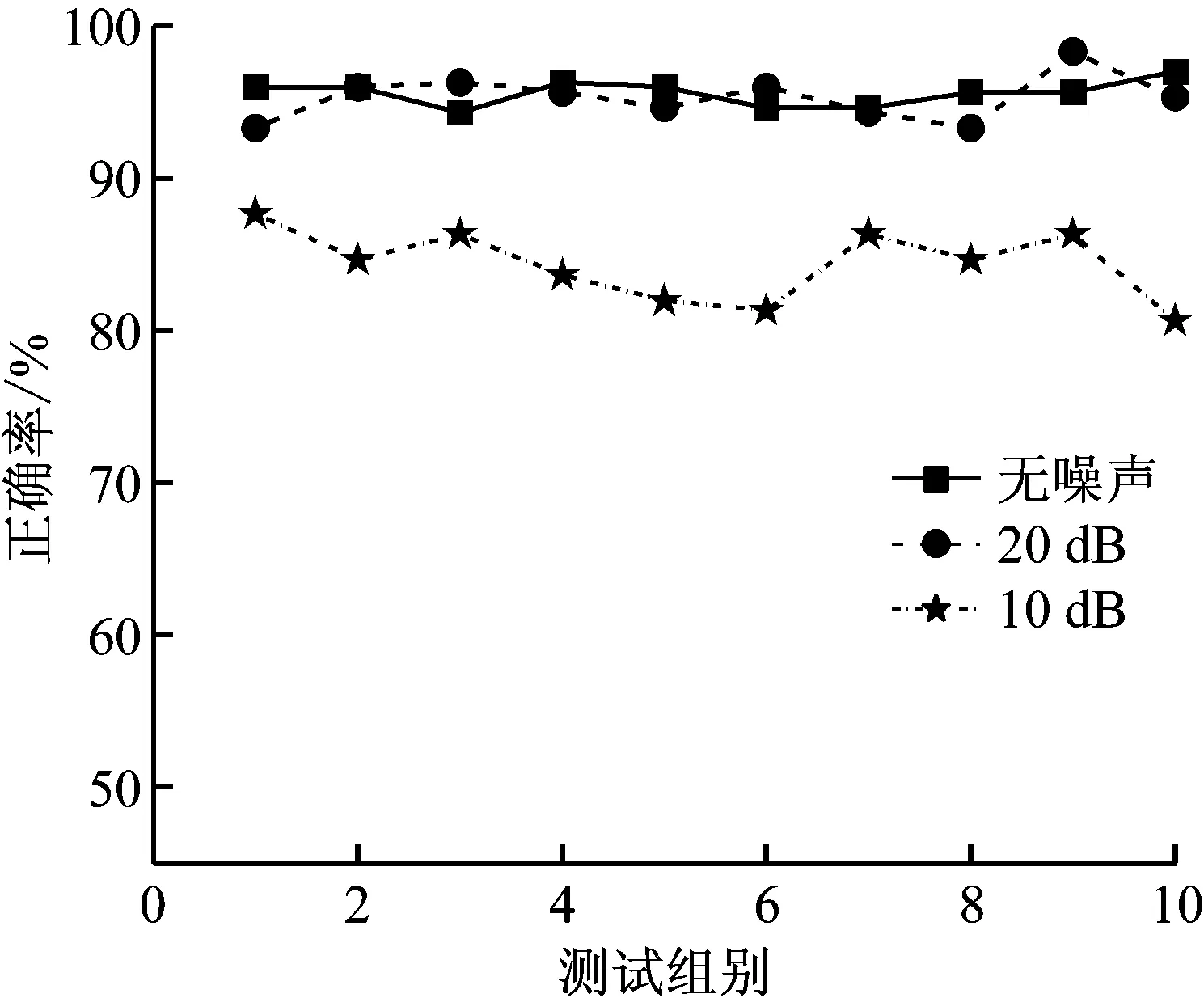
图11 带噪声数据集故障识别结果Fig.11 Results of fault recognition under noises with bigger dataset

4 结论

本文提出了一种基于STFT和CNN的滚动轴承故障诊断方法。将故障信号的预处理，特征提取和分类结合在一起，一定程度上实现了端到端的轴承故障诊断。首先根据滚动轴承故障特征频率选择合适的样本长度和STFT的窗口宽度，然后用遍历的方法，在LetNet-5模型的基础上选择合适的网络参数，构建适应于轴承故障诊断的CNN模型。通过滚动轴承故障模拟试验验证了：