一种基于环的串行级联CPM方法

马子骥，卢 浩，董艳茹

(湖南大学 电气与信息工程学院，长沙 410082)

0 引 言

近年来，随着通信技术与航空事业的快速发展，后舱通信的需求急剧增加，空中WIFI上网的概念开始浮现。实现旅客空中接入的诉求要求未来航空通信系统具备宽带传输能力和更广泛的互联互通能力。然而，航空公司的民航航线、航班日益增加导致了航空通信系统间的互干扰日益严重[1-2]。

连续性相位调制(continuous phase modulation，CPM)方式相对于传统的幅度键控(amplitude shift keying，ASK)、脉冲幅度调制(pulse amplitude modulation，PAM)、正交幅度调制(quadrature amplitude modulation，QAM)等技术，波形连续频谱集中，因而有更大的带宽利用率；包络恒定使得CPM信号对非线性信道引起的非线性失真不敏感，因此，适用于瑞丽衰弱信道或者是严重多径衰弱的场景中[3]；网格编码能与外编码级联，使得系统能够利用软信息迭代译码来改善误比特性能[4]。在Rimoldi分解模型[5]的基础上，Moqvist P[6]引入串行级联卷积码(serially concatenated convolutional code，SCCC)的串行级联结构实现了一种串行级联连续性相位调制方案。串行级联连续性相位调制(serially concatenated continuous phase modulation，SCCPM)系统有效地结合了SCCC和CPM的优点，能获得更高的编码增益。近年来，有学者利用多调制指数代替单调制指数方案[7]，以及引入干扰对齐的方式到SCCPM系统中[8]，来改善系统误比特性能。

本文从级联编码的角度，在兼顾航空通信系统带宽利用率的同时，设计了一个能有效降低同距离通信所需的发射功率的SCCPM方案。

1 CPM原理

1.1 CPM分解模型

根据文献 [5]，CPM信号的带通信号可表示为

(1)

(2)

(1)—(2)式中：kT≤t≤(k+1)T；fc为补偿后的载波相位；φ0为信号初始相位；Es为一个周期内的码元能量；W(τ)是分解模型中的数据无关项。

由(1)式和(2)式，CPM可以分解为一个有限状态的连续相位编码器(continuous phase encoder，CPE)和一个无记忆调制器 (memoryless modulator，MM)，如图1所示。

图1 CPM分解模型Fig.1 CPM decomposition model

1.2 CPM错误事件

分解模型下的CPM系统，由基于网格编码的连续性相位编码器和无记忆调制器实现。当译码检测的路径偏离原来的CPE编码路径时，便会产生错误的译码，发生CPM错误概率事件。在CPM调制中，网格编码并不会产生均匀错误概率事件[9-10]。当计算其错误事件时，需要考虑所有的可能检测路径与编码路径组合。根据文献[7]，CPM错误事件仅仅和差分符号序列相关，可以由归一化欧氏距离和来评价。

一个长度为N的CPM错误事件的相应归一化平方欧式距离和表述为

(3)

(4)

(5)

当系统发生错误事件时，差分比特序列为非全零序列。通过映射器，比特序列被映射成符号序列。因此，也可以通过相应的方式将差分比特序列转化为相应的差分符号序列。转化的规则为比特对应的绝对值乘以权值再加上符号，将对应的k比特转化为2k进制数。例如差分比特组{-1,1}将被映射成相对应的差分符号-1×2+1=-1。

图2 卷积码(7,5)差分符号示意图Fig.2 Differential symbols diagram of convolutional codes (7,5)

2 基于环的SCCPM方案

本节将基于环的卷积编码与CPE结合，构成基于环的CPM方案，与此同时作为内编码，设计一种基于环的SCCPM系统方案，如图3所示。在发送端，信息序列通过模p环的卷积编码器，输入到基于改进CPE的CPM调制系统中得到输出。在增大CPE的最小距离的同时，避免了符号映射。在接收端通过软输入软输出Log-MAP迭代译码的方式实现译码。

图3 基于环的SCCPM系统框图Fig.3 Diagram of the ring-based SCCPM system

2.1 基于环的卷积码

根据卷积码的编码原理[11]，基于模p整数环的递归卷积码实现方案如图4所示。

图4中，ak和bk分别是系统的输入和输出。系统中“+”代表模p加法。相对于传统卷积码，基于环的卷积码是多进制卷积编码方式，是在模p整数环上完成的卷积编码。编码码率为(l-1)/l，其通用的系统函数为

(6)

图4 环卷积码通用框图Fig.4 Diagram of thering-based convolutional code

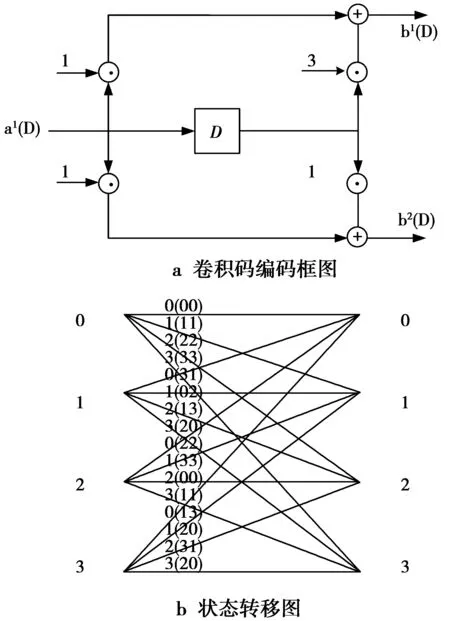
图5 [1+3D 1+D]卷积码编码框图和状态转移图Fig.5 Diagram and state transition diagram of convolutional code

2.2 基于环的CPM方案

针对M=PkM进制的MCPM系统，根据进制数的概念，可以将M进制数p基展开[12]。根据图1，将CPE分解模型输入码元Uk按照基p的形式展开为

(7)

每个输入序列Ui∈{0,1,…,M-1}对应着kM个p进制数。因此，得到的CPE编码结构如图6所示。该结构由kM级模p运算器以及kM×(L-1)+1级延迟单元构成，输入码元Uk逐级通过模p运算器之后被分解，并且输入延迟单元经过L-1级延迟单元输出。

图6 基于模p整数环的CPE结构Fig.6 CPE structure based on modulo p integer ring

在这仅考虑L=1的情况，基于模p整数环的无反馈CPE结构如图7所示。相应的CPM分解模型和CPE结构分别见图7a和图7b。其相应的生成矩阵可以表示为

(8)

(8)式中,IkM-1为单位矩阵。然而此结构下，CPE仍然带有负反馈，因此，可以在CPE结构之前引入预编码器，并且将模p运算移到预编码器端或者在预编码器前直接由映射器完成。其相应的结构见图7c。该预编码器的生成矩阵可以表示为

(9)

将预编码器与CPE级联将产生一个等效的无反馈CPE编码器，相应的框图见图7d，其生成矩阵为

C′(D)=T(D)C(D)=

(10)

将环的卷积编码与CPM中的无反馈CPE编码结合[13]，构成改进的CPE结构。对于调制指数3/4的4CPM，可以设计出很多种码率为1/2的模4环卷积编码结构与无反馈CPE的结合。以生成矩阵为G(D)=[1,1/1+2D]的卷积码为例，基于模4环的卷积码编码的状态转移图及改进CPE的状态网格如图8所示。改进的CPE可以等效为一个码率为1/4的编码器，其状态网格随着卷积码与无反馈CPE合并而合并。在合并之后，改进CPE网格状态数4远小于16(N=pv·pL)，其每个输入对应着4个输出。表1列出了环卷积码编码效率为1/2，调制指数为3/4时，其他合理的环卷积码的设计方案及其合并编码后的最小欧式距离，并与分解模型下CPM编码方案的最小欧式距离进行了对比。

图7 基于模p整数环的无反馈CPE结构Fig.7 Non feedback CPE structure based on modulo p integer ring

图8 基于环的CPM调制方案Fig.8 Modulation scheme of ring-based CPM

3 性能比较与差异分析

在高斯信道下，基于环的SCCPM方案和对照方案的实验条件同时设置为卷积码的码率为1/2，调制方案的记忆长度L=1，调制阶数M=4，调制指数h=3/4，脉冲成形函数g(t)为RC(升余弦脉冲)，基于环的SCCPM方案的外编码卷积码生成矩阵选择为[3D2+D+2,2D+3]，基于环的CPM的卷积码生成矩阵为[1,1/1+2D]，对照组的二进制卷积码生成矩阵为(7,5)8。系统实验条件的选取需要兼顾带宽利用率与功率利用率，与此同时还要考虑系统的设计复杂度。即在保证带宽利用率和功率利用率的前提下，选择合适的参数，使得系统的复杂度最低。其中，增大关联程度L可以适当降低CPM的功率谱密度，但是，随着L的迅速增大，导致CPE网格的状态数呈指数型增长，使得CPM的实现复杂度、计算复杂度与存储复杂度呈指数型增长；采用升余弦脉冲成形函数可以使得CPM信号的功率谱旁瓣下降迅速，能有效抑制带外功率来提升信号的抗噪声能力；同时，CPM系统的状态个数会随着调制阶数M的增大，呈指数型增长，从而增大解调的复杂度；此外，随着调制指数h的增大，将导致CPE编码网格的状态数增大，CPE网格编码与SISO-CPE软译码的时间复杂度与计算复杂度将增大。

表1 编码效率为1/2，调制指数为3/4时环卷积码最小距离

根据试验分析，随着迭代次数的增加，系统的误码率曲线不断下降并趋于收敛；而且随着信噪比的增加，迭代次数对误码率性能的影响越来越明显，当迭代次数大于5次之后，继续迭代对系统的性能改善并不明显，及时地停止迭代可以降低译码过程的计算与时间消耗。经过试验，本文选用的最佳迭代次数为5次,CPM与卷积码的译码方式都为Log-MAP算法。交织方式为伪随机交织。

图9 不同方案系统性能对比Fig.9 Different system performance

对于基于模4环的卷积码串行级联CPM系统，其性能提升的主要原因有以下2方面。

1)同样约束度下，基于环的卷积编码对于二进制卷积编码有更大的自由距离；当交织长度足够大的情况下，自由距离较大的卷积码能更有效地改善系统误比特性能。此外，由表1可知，基于环的CPM系统对于同样参数下的传统CPM最小自由距离也相应增大，意味着基于环的CPM方案拥有更小的差错率。

2)基于模4环的卷积编码输出序列为4进制符号序列，根据CPM差错事件分析可知在符号交织后并不会改变这些差分符号。因为在符号交织时，4进制相邻位置的2比特保持位置不变，当发生CPM错误时，符号交织并不会改变其对应的差分符号。而基于二进制卷积编码后输出为比特序列，合并的任意性将导致所有可能的差分符号。由CPM错误事件分析可知，整个SCCPM系统的错误概率事件是由差分符号序列决定，因此，基于模p环的卷积编码，将产生更少的错误事件。

4 结 论

本文在传统的SCCPM基础之上，提出了一种基于环的串行级联CPM方案。该方案利用基于环的多进制卷积编码和基于环的CPE分别作为内外编码，通过符号交织、迭代译码的方式来获取级联增益。通过仿真分析，与传统二进制SCCPM方案对比，基于环的SCCPM方案有1.25～1.75 dB的增益。并且文章从最小距离和错误概率事件的角度分析了性能差异，证明了其有更好的误比特性能，即到达相同既定通信距离时系统的发射功率更低。针对航空通信系统面临航线与航班日益增多带来的通信系统互干扰，本方案能有效降低其同距离通信所需的发射功率，具有良好的应用前景。