基于类间功率谱差的FRFT-TDCS门限判决算法
2018-10-19任清华徐兵政王桂胜胡诗骏
任清华,徐兵政,王桂胜,胡诗骏,刘 洋
(1.空军工程大学 信息与导航学院,西安 710077;2.中国电子科技集团 航天信息应用技术重点实验室, 石家庄 050081;3.95129部队,河南 开封 475000)
0 引 言
变换域通信系统(transform domain communication system,TDCS)以其独特的利用频谱空穴“主动”抗干扰的思想和低截获(low probability of interception, LPI)、低检测(low probability of interception, LPD)性能引起了通信领域内的广泛关注[1-4]。近几年来,FRFT作为一种新兴的时频变换工具,不断得到完善和发展,成为了对LFM信号良好的处理工具。文献[5]将FRFT引入TDCS,开启了分数阶傅里叶变换域通信系统(transform domain communication system based on fractional Fourier transform, FRFT-TDCS)的崭新时代。
变换域通信系统“主动”抗干扰能力主要体现形式是在变换域上将干扰有效地剔除。因此,门限的设定决定了干扰是否能彻底剔除。传统的TDCS门限设置方法以干扰信号最大频谱幅度的40%作为门限值对干扰频谱进行剔除。国内许多学者在TDCS门限上做出贡献,但是大多是基于傅里叶变换的传统TDCS的基础上。目前,有关FRFT-TDCS的门限设计的文献极其有限,文献[6]利用FRFT-TDCS对单分量线性调频(linear frequency modulation,LFM)干扰进行处理,首先确定最优变换阶次,再进行门限设置,但是在多分量LFM干扰的情况下,不同LFM干扰信号由于最优变换阶次的不同,导致在不同变换阶次下的干扰频谱幅度和位置均不同,难以有效剔除干扰。文献[7]对噪声进行估计,从而自适应地确定门限,达到降低误码率的目的,但是忽略了干扰条件对噪声估计的影响,且没有说明噪声估计的方法。本文从干扰与噪声的特征出发,利用 “类间方差最大既是错分概率最小”的思想[8],根据类间方差算法仅以均值为特征的缺陷,提出类间功率谱差算法,无需对噪声有先验知识。仿真结果表明,该算法能较大地改善系统的抗干扰能力。
1 LFM干扰分数域频谱特征
1.1 分数阶傅里叶变换定义
信号x(t)的α角度的FRFT定义为

(1)
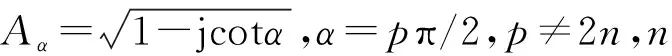
1.2 线性调频干扰定义
LFM干扰是一种典型的非平稳干扰信号,其瞬时频率随时间呈线性变化,多分量LFM干扰可表示为
(2)
(2)式中,ki,fi,Ai分别代表第i个分量LFM干扰信号的调频率、初始频率、幅度。图1为LFM干扰信号的时频分布图。

图1 LFM干扰信号时频分布图Fig.1 Time frequency distribution of LFM interference
图1中,加粗黑线代表了LFM干扰的时频分布,α代表了LFM干扰在时频分布图上旋转的角度。采用文献[9]中的方法对电磁环境中的多分量LFM干扰信号参数进行估计,第i分量LFM干扰信号的最优阶次可计算为
(3)
图2为LFM干扰信号的FRFT域频谱分布图。可以看出,多分量LFM干扰由于调频率ki的不同导致各分量的最优阶次不一致,不同分量LFM干扰仅在其最优阶次时,其FRFT域频谱取得最大值,且明显大于其他变换阶次,其他的分量由于远离其最优阶次,导致FRFT域峰值呈下降趋势。

图2 LFM干扰信号的FRFT域频谱分布图Fig.2 FRFT domain of LFM interference
不同变换阶次下三分量LFM干扰信号的频谱分布如图3所示。可以看出,多分量LFM干扰信号在不同变换阶次下的分数域频谱分布截然不同,根据传统的门限设置方法将干扰信号最大频谱幅度的40%作为门限值(见图3中直线),必将导致部分干扰频谱难以被有效剔除,造成系统性能下降。为此,本文提出自适应的门限设置方法,能够有效剔除干扰频谱。
2 FRFT-TDCS工作原理
由于傅里叶变换在处理非平稳干扰时具有局限性,而FRFT作为一种时频分析工具对LFM干扰良好的处理能力,因此,FRFT-TDCS相比于FFT-TDCS(transform domain communication system based on Fourier transform)具有无可替代的作用,其工作原理如图4所示。
2.1 FRFT-TDCS基函数生成算法
发送端首先将电磁环境在FRFT域进行采样,对干扰信号参数估计,以相位u和变换阶次p为变量,生成[u,p,X(u,p)]三维分数域频谱分布图;选择最优阶次p,同时确定门限值,门限设置可以对干扰频谱进行判决,小于门限值的频谱载波进行保留,设置为1,大于门限值的频谱载波进行剔除,设置为0,得到由0,1序列组成的幅度谱向量A′(k);将伪随机相位ejθk与幅度谱A′(k)相乘生成基函数,表示为
(4)

图3 不同变换阶次下三分量LFM干扰信号分数域频谱分布图Fig.3 Spectrum distribution of three component LFM interference signal under different FRFT orders
为保证每一调制波形均能够以相同的功率进行发射,系统需要对FRFT域基函数进行能量调整
(5)
(6)
(6)式中,ejπφp为FRFT变换核。可以从图2中看出,FRFT-TDCS基函数具有伪随机特性,另外,系统对FRFT域的干扰频谱进行定周期检测,其FRFT域幅度谱向量会根据干扰频谱的变化不断进行更新,对应的基函数也会不断更新,因此,可以始终保持良好的抗干扰能力。在接收端,认为其所处的电磁环境相同(例如蜂群无人机数据链抗干扰通信)。采用相同的方式,可以得到与发射端同样的基函数,进而对信息位进行恢复,FRFT-TDCS基函数时域图如图5所示。
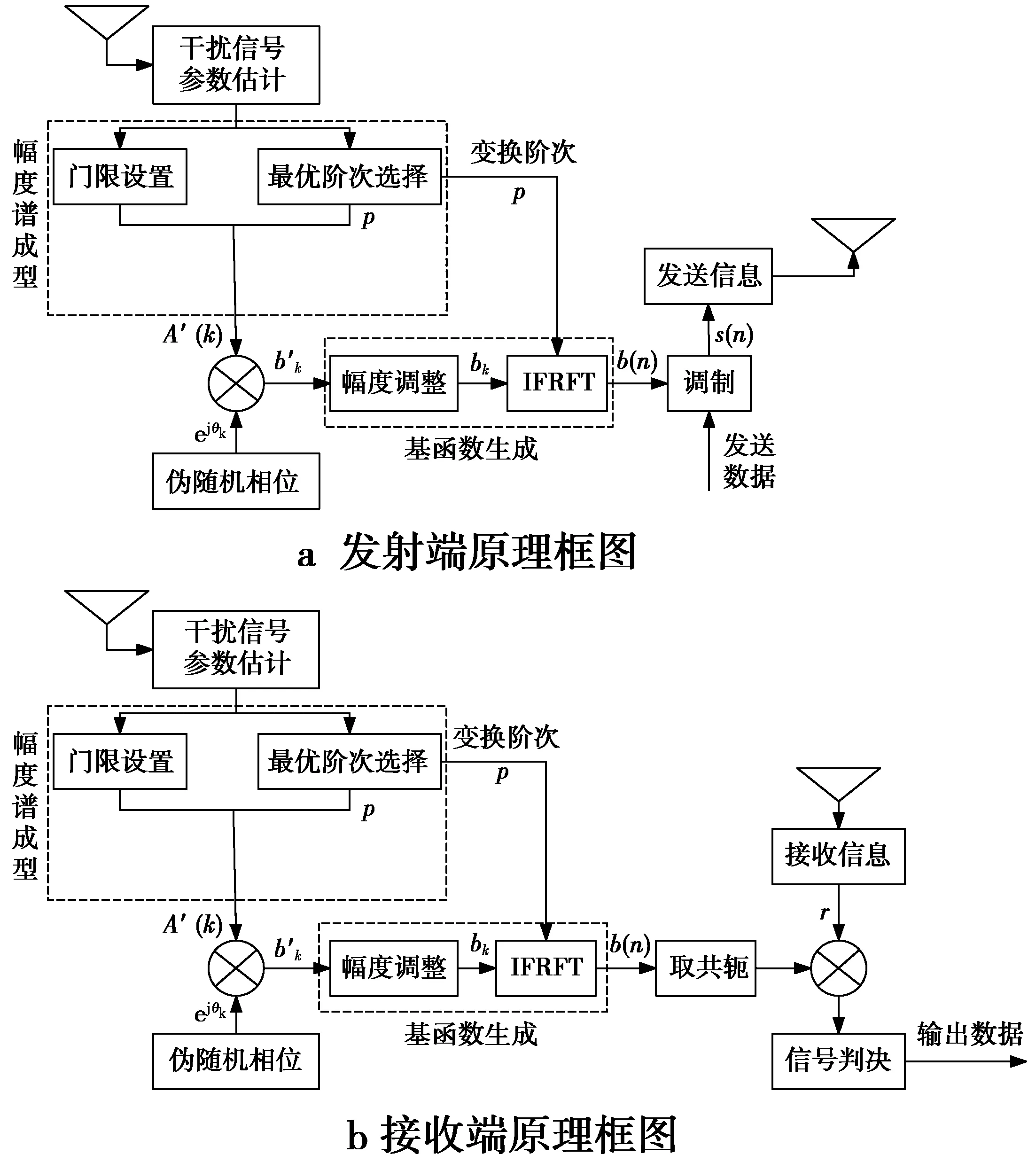
图4 FRFT-TDCS工作原理框图Fig.4 Working principle diagram of FRFT-TDCS
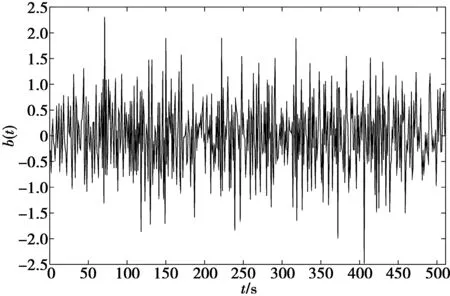
图5 FRFT-TDCS基函数时域图Fig.5 Base function time domain graph of FRFT-TDCS
2.2 调制技术
与传统的通信系统不同,TDCS没有使用载波调制。而是根据信道特征所设计的具有类噪声性能的基函数对信息数据进行调制,以满足系统对LDI/LDP性能的要求。下面对TDCS 2种主要的调制方式的误码率进行研究。
现有的调制技术有双极性(Bipolar)调制、循环移位键控(cyclic shift keying,CSK)调制、以及CSK的改进形式。Bipolar调制是一种简单的调制方式,其将基函数进行翻转,用基函数的正负代表不同发送码元si,解调程序简单,误码率性能较好,但传输效率极低。CSK是利用基函数良好的类噪声性能,将基函数不同移位后的波形生成一个数量庞大发送波形集合,每一发送波形均可以对多个信息位进行调制,提高了频谱利用效率。Bipolar调制和CSK对比如表1所示。

表1 不同调制技术对比
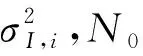
(7)
M为CCSK的调制阶数.则基于CSK调制的TDCS系统误比特率可表示为
(8)

3 基于类间功率谱差的门限判决算法
FRFT-TDCS和扩频通信相比,不再是盲目地利用整个频谱,而是利用FRFT域剔除干扰后的“干净”频谱,具有良好的抗干扰能力。如果门限判决过高,导致干扰未必剔除,造成误码率的必然增高;如果门限判决过低,可能导致剔除不存在干扰的频段,导致频谱率用率降低。
3.1 算法描述
首先,由于在文献[10]中证明FRFT不改变白噪声的统计特性,白噪声不跟随分数阶傅里叶变换的变换阶次而改变。因此,高斯白噪声的幅度不会随着变换阶次的变化而变化。
其次,令相位搜寻点数为u,FRFT变换阶次搜寻点数为v,假设信道中存在LFM干扰j(t)和噪声n(t)
x(t)=j(t)+n(t)
(9)
对x(t)进行变换角度为α的FRFT变换
X(u,α)=J(u,α)+N(u,α)
(10)

(11)
利用门限值k,幅度值被分到L1(0≤i≤k)的概率P1(k)为
(12)
那么分配到L1的分数阶功率谱为
(13)
根据贝叶斯公式得出
(14)
由于设定i的值是来自L1,故P(L1/i)=1。
(15)
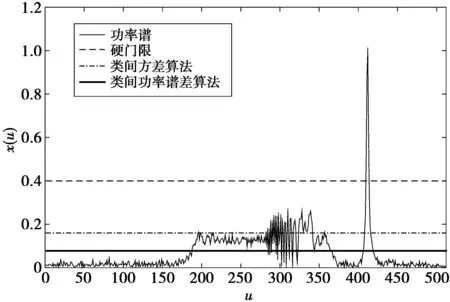
类似地,分配到L2(k (16) 整个分数域三维分布图的分数阶功率谱为 (17) 联合(12),(15)—(17)式可以得到 P1(k)R1+P2(k)R2=RG (18) P1(k)+P2(k)=1 (19) 引进类间功率谱差的概念,定义为 Z(k)=P1(k)(R1-RG)2+P2(k)(R2-RG)2 (20) 将(18) 式和(19)式代入(20)式,可以得出 Z(k)=P1(k)P2(k)(R1-R2)2 (21) 从(21)式可以看出,R1与R2相差越大,Z的值越大,这表明类间功率谱差和类间方差相似,都可以代表类之间的可分性度量,只是类间方差以均值为特征,类间功率谱差以功率谱为特征。因此,寻找最优门限k*使得Z(k)的值最大化。即为了寻找k*,对所有的k的整数值进行计算,并选取使得Z(k)最大的k值。 门限设置步骤描述如下。 1)将电磁环境在FRFT域进行采样。使用p(i)表示幅度值为i的概率; 2)设定门限值为k,计算幅度值i小于k的概率P1和分数阶功率谱R1;计算幅度值i大于k的概率P2和分数阶功率谱R2; 3)利用遍历搜索,将k从0到L-1(即幅度值i的最大值)进行取值,并计算类间功率谱差Z(k)=P1(k)P2(k)(R1-R2)2; 4)得到最佳门限k*,即使Z(k)取得最大值的k值。 P1(k)需要k+1次加法,P2(k)需要L-k-1次加法,R1需要k+1次加法,2k+3次乘法和1次除法,R2需要L-k-1次加法,2L-2k-1次乘法和1次除法,因此,根据(21)式,类间功率谱差算法根据门限值k单次运算量为:加/减法2L+1次,乘/除法2L+7。依此类推,类间方差算法单次运算量为:加/减法2L+1次,乘/除法L+7。虽然相比较类间方差算法,类间功率谱差算法复杂度略高,但是在大干信比情况下抗干扰性能增益尤为明显。 仿真参数设置:①信道模型为加性高斯白噪声信道,固定信噪比为4 dB;②选取9阶线性移位反馈寄存器产生的m序列作为伪随即序列,本原多项式系数向量为[1 1 1 0 1 1 0 0 1] ,移位寄存器初始状态为[0 0 0 0 0 0 0 0 1];③所传输的信息序列为一个长度为10 000的随机序列,迭代次数为1 000次;④LFM干扰信号的时间取值为[-2,2],采样频率fs为128 Hz,采样点数为512(与基函数一致),干扰信号为三分量LFM干扰,调频率k分别为8,12,20 Hz/s,初始频率f0分别为40,15,5 Hz,初始相位均为0 rad,图6为对应的阶次为1.16时,干扰的功率谱图。 图6 阶次为1.16时干扰的功率谱图Fig.6 Power spectrum of interference at order 1.16 从图6可以看出,硬门限是根据峰值40%所设置。对于多分量LFM干扰信号,仅能剔除最优变换阶次为1.16的LFM干扰,严重造成干扰频谱漏检。类间方差算法相比较硬门限有较好的改善,但仍然难以完全剔除干扰,改进的类间功率谱差算法以噪声和干扰的功率谱为特征,较前2种算法均有提高,可以有效剔除干扰频谱。图7,图8分别表示在Bipolar调制、CSK调制下FRFT-TDCS的误码率。 图7 Bipolar调制误码率Fig.7 Bit error rate of Bipolar modulation 仿真结果表明,在Bipolar调制、CSK调制下类间方差和类间功率谱差算法较传统硬门限判决算法,误码率均有所改善;类间功率谱差算法对干扰频谱剔除效果明显好于类间方差算法,尤其在大信干比情况下,仍然可以保持较好的误码率。 图8 BCSK调制误码率Fig.8 Bit error rate of BCSK modulation 针对FRFT-TDCS应对多分量LFM干扰信号难以有效识别干扰的问题,受类间方差启发,利用噪声和干扰分数域功率谱的明显差异,提出了类间功率谱差算法,在FRFT域三维频谱分布图上自适应地确定FRFT-TDCS门限值。仿真结果表明,该算法可以有效区分噪声和干扰,不仅避免了FRFT变换阶次对门限判决的影响,在误码率性能方面也具有明显的优势。3.2 复杂度分析
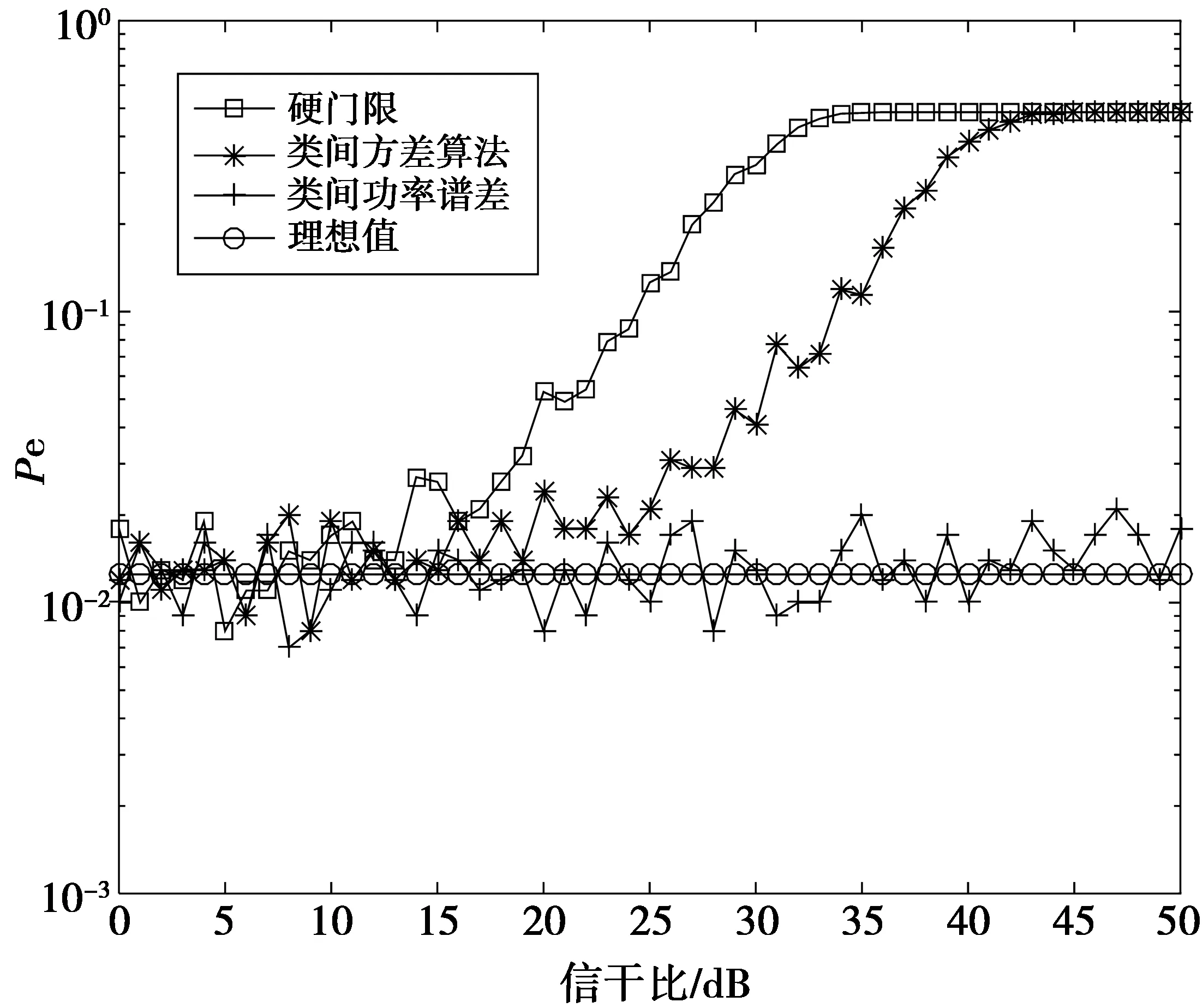
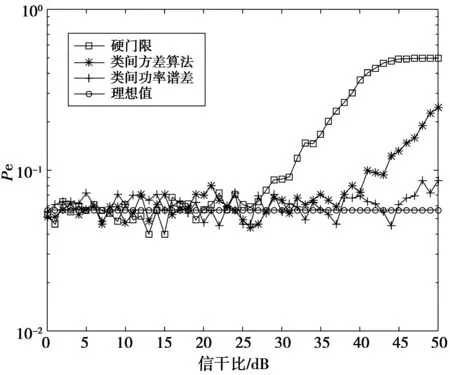
4 性能分析与仿真验证
5 结 论
