三元一阶常系数线性微分方程组的解构造*

赵 临 龙

(安康学院数学与统计学院，陕西 安康 725000)

0 序 言

对于三元一阶线性微分方程组：

(1)

一般都是用基解矩阵，先求出方程组(1)对应的齐次方程组的解，再利用常系数变异法求出方程组(1)的解，这些方法都比较繁琐.[1-14]文献[15]对于n元一阶线性齐次微分方程组的解法进行研究，得到相关结论.本文将对三元一阶线性非齐次微分方程组解法进行深入讨论，给出其解的本质结构.

1 方程组(1)的解结构

对于方程组(1)，设x=(x1,x2,x3)T，f=(f1,f2,f3)T，K=(k1,k2,k3)，其中k1,k2,k3是不全为零的常数，使得

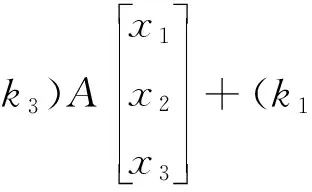
(4)

(k1a12+k2a22+k3a32)x2+(k1a13+k2a23+k3a33)x3+(k1f1+k2f2+k3f3).

(5)

令

k1a1i+k2a2i+k3a3i=λki(i=1,2,3,λ为常数)

(6)

(7)

定义1对于常系数线性方程组(1)，设U=(k1,k2,k3)T，其中k1,k2,k3是不全为零的常数，使得

(A-λE)TU=0⟺UT(A-λE)=0,

(8)

则方程A-λE=0称为方程(1)的特征方程，而将满足(8)的K=(k1,k2,k3)称为特征根λ所对应的特征“行向量”.

结论1[15]设n阶矩阵A的特征根λ的重数为m,则方程组(1)对于常数列向量u1的m-1个广义列向量ui(i=1,2,…,m)满足

(9)

结论2[3]设m阶矩阵A的特征根λ的重数为m,则

(A-λE)m=0.

(10)

定理1如果常系数线性齐次方程组(1)的特征方程(A-λE)=0有3个互异的特征根λ1,λ2,λ3，而λ1,λ2,λ3对应的线性无关的特征行向量分别为Ki=(ki1,ki2,ki3)(i=1,2,3)，则(1)化为代数线性方程组

(i=1,2,3).

(11)

定理2如果常系数线性齐次方程组(1)的特征方程A-λE=0有特征重根λi(i=1或2),其重数分别为m1,m2,m1+m2=3，而对应的线性无关的特征行向量为Km,Km-1(m=2或3)，则(1)化为一阶线性齐次方程

(12)

其中特征根λi对应特征行向量为Ki.

证明：若方程组(1)的特征方程A-λE=0特征根为λi，对应的线性无关的特征行向量Ki=(ki1,ki2,ki3)(i=1,2,3)满足

(13)

则有代数线性方程

, (i=1,2,3).

(14)

即定理1获得证明.

现在，若方程组(1)的特征方程A-λE=0特征根λ为m重根，由结论1，得方程

(A-λE)um=0.

(15.1)

(A-λE)um-1=um.

(15.2)

对于方程组(1)的齐次形式x′=Ax，在(15.2)中，其线性无关的解xm-1=um-1eλt、xm=umeλt(m=2或3)满足方程

λExm-1+xm, (m=2或3).

(16)

1° 对于(A-λiE)xm=0(i=1或2)，由定理1将方程组(1)化为一阶线性方程形式

(Kixm)′=λi(Kixm)+Kif,

(17)

其中特征根λi的对应特征行向量为Ki，i=1或2.

2° 对于(A-λiE)xm-1=xm(m=2或3,i=1或2)，则

λixm-1+xm,

(m=2或3;i=1或2),

(18)

其中xm(m=2或3)为满足(17)的解.

(A-λiE)mum-1=0, (m=2或3).

(19)

对于特征根λi，取对应线性无关的特征行向量为Km-1,有：

Km-1(A-λiE)m=0, (m=2或3，i=1或2).

(20)

于是，有方程

,(m=2或3).

(21)

(Km-1xm)′=λi(Km-1xm)+Km-1(A-λiE)xm-1+

Km-1f.

(22)

此时，由(2°)得到

(Km-1xm-1)′=λi(Km-1xm-1)+Km-1xm+Km-1f,

(m=2或3,i=1或2),

(23)

其中xm为满足(17)的解.

即方程组(1)的化为以下形式

(23)

其中特征根λi对应特征行向量为Ki,m=2或3，i=1或2.证得定理2.

此时，由Ki(A-λiE)m=0(i=2或3)确定Ki.

(1)若(A-λiE)2≠0(i=1)，在(23)中，取Km与Km-1(m=2或3)构成线性无关的行向量，即可.

(2)若(A-λiE)2=0(i=1)，由结论，在(23)中，直接取取Km与Km-1(m=2或3)构成线性无关的行向量，即可.最简单的是直接取单位分向量.

推论如果常系数线性齐次方程组(1)的特征方程A-λE=0有特征根λ重数为3，而对应的线性无关的特征行向量为K，若(A-λE)2=0，则(1)化为一阶线性齐次方程

(24)

其中KI为取单位分向量(1,0,0),(0,1,0),(0,0,1)即可.

2 方程组(1)解理论的应用

例1[4]解方程组

解 由特征方程A-λE=-(λ-1)(λ+2)(λ+3)=0，得到特征根λ1=-1,λ2=-2,λ3=-3.

设λ1=-1所对应的特征行向量K1=(k11,k12,k13)满足

k11-6k13=0,k11+k12-11k13=0,k12-5k13=0.

求得K1=(6,5,1)，有方程

(6x1+5x2+x3)′ =K1Ax+K1f

=-6x1-5x2-x3+e-t，

6x1+5x2+x3=C1e-t+te-t.

(1.1)

设λ2=-2所对应的特征行向量K2=(k21,k22,k23)满足

2k21-6k23=0,k21+2k22-11k23=0,k22-4k23=0.

求得K2=(3,4,1)，有方程

(3x1+4x2+x3)′ =K2Ax+K2f

=-6x1-8x2-2x3+e-t,

3x1+4x2+x3=C2e-2t+e-t.

(1.2)

设λ3=-3所对应的特征行向量K3=(k31,k32,k33)满足

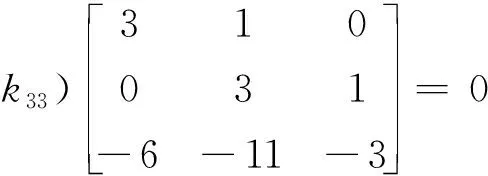
3k31-6k33=0,k31+3k32-11,k33=0,k32-3k33=0.

求得K3=(2,3,1)，有方程

(2x1+3x2+x3)′ =K3Ax+K3f

=-6x1-9x2-3x3+e-t,

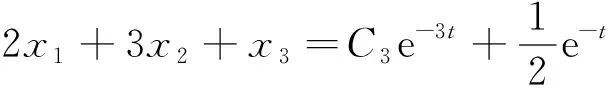
(1.3)

由(1.1)、(1.2)、(1.3)，得到初始条件：x(0)=o的方程组

于是，求得原微分方程组的解

.

例2[3]解方程组

解 由特征方程A-λE=-(λ+1)3=0，得到特征根λ1=λ2=λ3=-1.

设λ1=-1所对应的特征行向量K1=(k11,k12,k13)满足

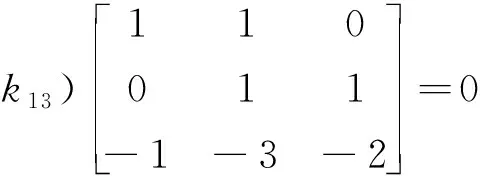
k11-k13=0,k11+k12-3k13=0,k12-2k13=0.

求得K1=(1,2,1)，有方程

(x1+2x2+x3)′ =K1Ax+K1f

=-(x1+2x2+x3)+(t-5)e-t,

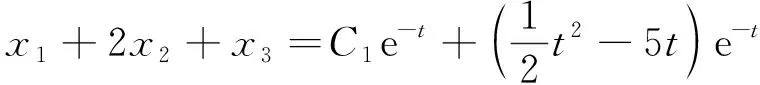
(2.1)

设λ2=-1所对应的特征行向量K2=(k21,k22,k23)满足

=(k21,k22,k33)0=0.

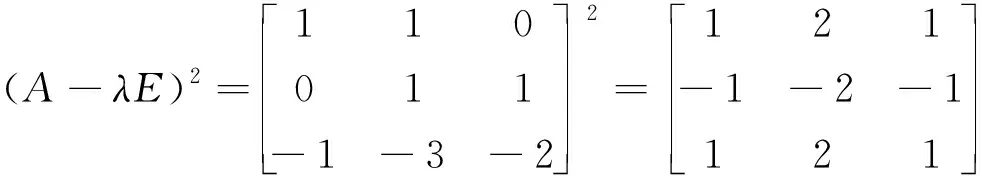
(x1+x2)′ =K2Ax+K2f=x2+x3

=-(x1+x2)+(x1+2x2+x3)

x2= (C2-C3)e-t+(C1-C2)te-t-C1t2e-t+

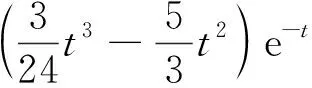
(2.2)

再取K3=(1,0,0)，有方程

(x1)′ =K3Ax+K3f=x2=-x1+(x1+x2)

(2.3)

由(2.1)、(2.2)、(2.3)，得到方程组的解

例3[13]解方程组

解 由特征方程A-λE=-(λ-3)3=0，得到特征根λ1=λ2=λ3=3.

设λ1=3所对应的特征行向量k1=(k11,k12,k13)满足

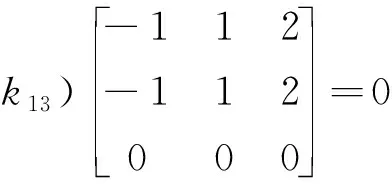
k11+k12=0.

求得k1=(1,-1,0)，有方程

(x1-x2)′=3x1-3x2=3(x1-x2),

x1-x2=C1e3t.

(3.1)

设λ2=3所对应的特征行向量k2=(k21,k22,k23)满足

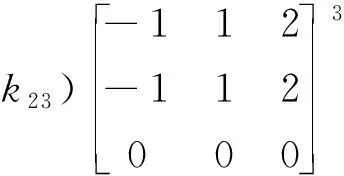
(x3)′=K2Ax=3x3,

x3=C2e3t.

(3.2)

再取单位分向量k3=(1,0,0)，有方程

(x1)′=K3Ax=2x1+x2+2x3=3x1-(x1-x2)+

2x3=3x1-C1e3t+2C2e3t,

C1te3t+2C2te3t.

(3.3)

由(3.1)、(3.2)、(3.3)，得到方程组的解

同样，可得到解(3.3).

3 理论的推广

结论1如果常系数线性非齐次方程组

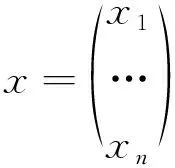
(25)

的特征方程(A-λE)=0有n个互异的特征根λ1,λ2,…,λn，而λ1,λ2,…,λn对应的线性无关的特征行向量分别为Ki=(ki1,ki2,…,kin)(i=1,2,…,n)，则方程组(25)化为方程组

(Kix)′=λi(Kix)+Kif(i=1,2,…,n),

(26)

其中特征根λi对应特征行向量为Ki,i=1,2,…,n.

结论2如果常系数线性非齐次方程组(25)的特征方程A-λE=0有不同的特征根λ1,λ2,…,λm,其重数分别为n1,n2,…,nm,n1+n2+…+nm=n，而λ1,λ2,…,λm对应的线性无关的特征行向量分别为Ki=(ki1,ki2,…,kin)(i=1,2,…,m)，则(25)

化为方程组

(27)

其中特征根λi对应特征行向量为Ki,i=1,2,…,m.