基于脉搏波传导时间和脉搏波特征参数的连续血压无创检测
2018-10-18赵彦峰于双王慧泉朱豪杰王金海
赵彦峰,于双,王慧泉,2,朱豪杰,王金海,2△
(1.天津工业大学电子与信息工程学院,天津 300387;2.天津市医学电子诊疗技术工程中心,天津 300387)
1 引 言
连续血压[1]测量可以实际反映血压在全天内的变化规律,对突发性心脑血管病的预测及对降压药的治疗效果评估有重要意义[2]。
连续血压直接测量法可实现连续血压的测量,被公认为血压测量的“金标准”,但技术要求高,且为有创测量,不能被广泛使用[3]。无创连续血压间接测量是通过分析人体相关特征信号,获取血压值的测量方法。动脉张力法[4]和容积补偿法[5]是两种常用的无创连续测量方法,但其长时间的测量会导致静脉充血而影响测量精度,其应用有一定局限性。基于脉搏波传导时间的连续无创血压测量是利用脉搏波传导时间与血压之间的相关性提出的一种间接测量法,测量装置简单,无袖带的充放气,有利于长时间的血压监测。早在1957年,Lansdown就提出对于某一个体,PTT与血压之间呈线性相关[6],由于不同个体之间的心脏和血管不同,测量会有较大的误差,但许多学者已经证明血压和脉搏之间存在密切的相关性[7]。本研究提取脉搏波特征参数,利用相关分析对脉搏波特征参数进行优化,将优化的脉搏波特征参数加入PTT与血压之间的校正模型中,以克服脉搏波特征的个体差异对本方法无创血压检测的影响。
2 基本原理
血压是在血液循环中,心脏周期性地射血,血液沿着主动脉流动时对血管壁所施加的压力[8]。血液在流动过程中产生周期性的脉搏波,脉搏波波形会随着离心脏距离的不同会有时间上的延迟即脉搏波传导时间,由Moens-Kortweg公式和Hughes[9]推导出人体血压变化与动脉血管壁杨氏弹性量以及脉搏波传导时间的关系[10]:
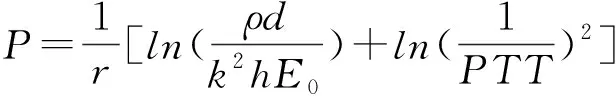
(1)
式中:P为血压值,E0为血压值为零时血管壁弹性模量,h为血管壁厚度,d为血管内径,ρ为血液密度,PTT为脉搏波传导时间,K为无量纲常数,γ为血管特性参数量值。
由上式可知,血压值和脉搏波传导时间具有较好的相关性,由脉搏波传导时间可以间接地得到血压值。见图1,A点为PTT的起点,D点为PTT的终点。
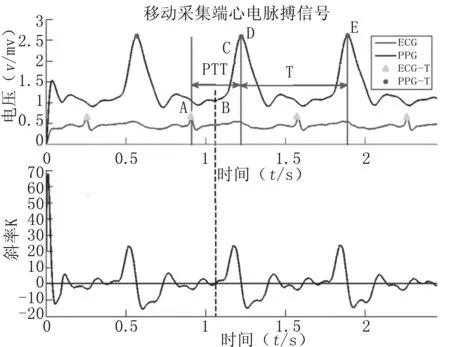
图1 脉搏波特征参数示意图
脉搏波的特征参数有很多,如幅值,时间特性等[11]。常见的脉搏波特征参数[12]有主波的高度h(即D点的幅值)、主波的上升时间t(tBD)、升支最大斜率近似值K(KC)、脉搏波的波形系数、每搏心输出量的特征参数(Z=(h×T)/(T-t))、脉搏波的周期T(TDE)等参数[13]。利用偏最小二乘法进行数据分析,从而间接的计算出血压值。
偏最小二乘法回归的基本作法是先在变量集中提出第一成分t1(t1是x1,x2…,xm的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分u1,并要求t1与u1相关程度达到最大。然后建立因变量y1,y2,…,yp与t1的回归,如果回归方程已达到满意的精度,则算法中止。否则继续第二对成分的提取,直到能达到满意的精度为止。若最终对自变量集提取r个成分t1,t2,…,tr,偏最小二乘法回归将通过建立y1,y2,…,yp与t1,t2,…,tr的回归式,再表示为y1,y2,…,yp与原自变量的回归方程式,即偏最小二乘回归方程。
3 数据采集及处理
脉搏波传导时间的计算关键在于脉搏波传输起点和终点的选择,一般可以采用心电信号的R波作为PTT的时间起点[14],在肢体末端如指尖等设置一光电传感器,记录光电脉搏波(PPG)[15],提取PPG信号的最大值为终点,从而得到延时时间PTT。本实验使用ANALOG DISCOVERY采集卡,双通道、14-Bit、125MSPS采样率,利用氯化银电极和反射式PPG传感器,分别采集50名志愿者的心电信号和脉搏波信号,通过姿态和饮食调整志愿者的血压值,共获得200组不同的血压值数据。被测者性别为25男25女,均为年龄在22~60岁之间,平均年龄为39岁,本研究所有的志愿者均被告知实验的详细内容并征得同意。在测量实验前被测人员应休息10 min,并且保持端坐的状态,使用欧姆龙HEM-7111测量血压,每个被测者测量四次血压,每隔十五分钟测量一次作为一组数据,这样可以避免一次偶然性误差对结果产生较大的影响。采集系统的整体设计见图2。
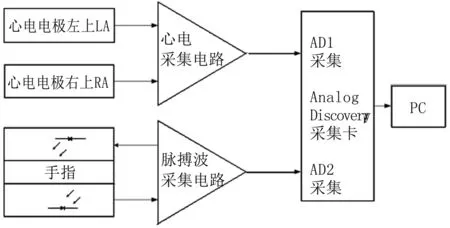
图2 系统整体设计
人体心电信号(ECG)和光电脉搏波信号(PPG)属于非常微弱的生理低频信号,其频率范围在0~30 Hz之间,其幅值范围在0~10 mV之间。人体自身阻抗大,且易受外界环境的影响,所以在采集过程中,采用高输入阻抗、高共模抑制比、低噪声、低温漂的前置放大器对心电信号和脉搏信号进行放大,放大之后的信号通过50 Hz的陷波滤波器滤除工频干扰和巴特沃斯低通数字滤波器进行滤波,获得较平滑的信号,见图3。
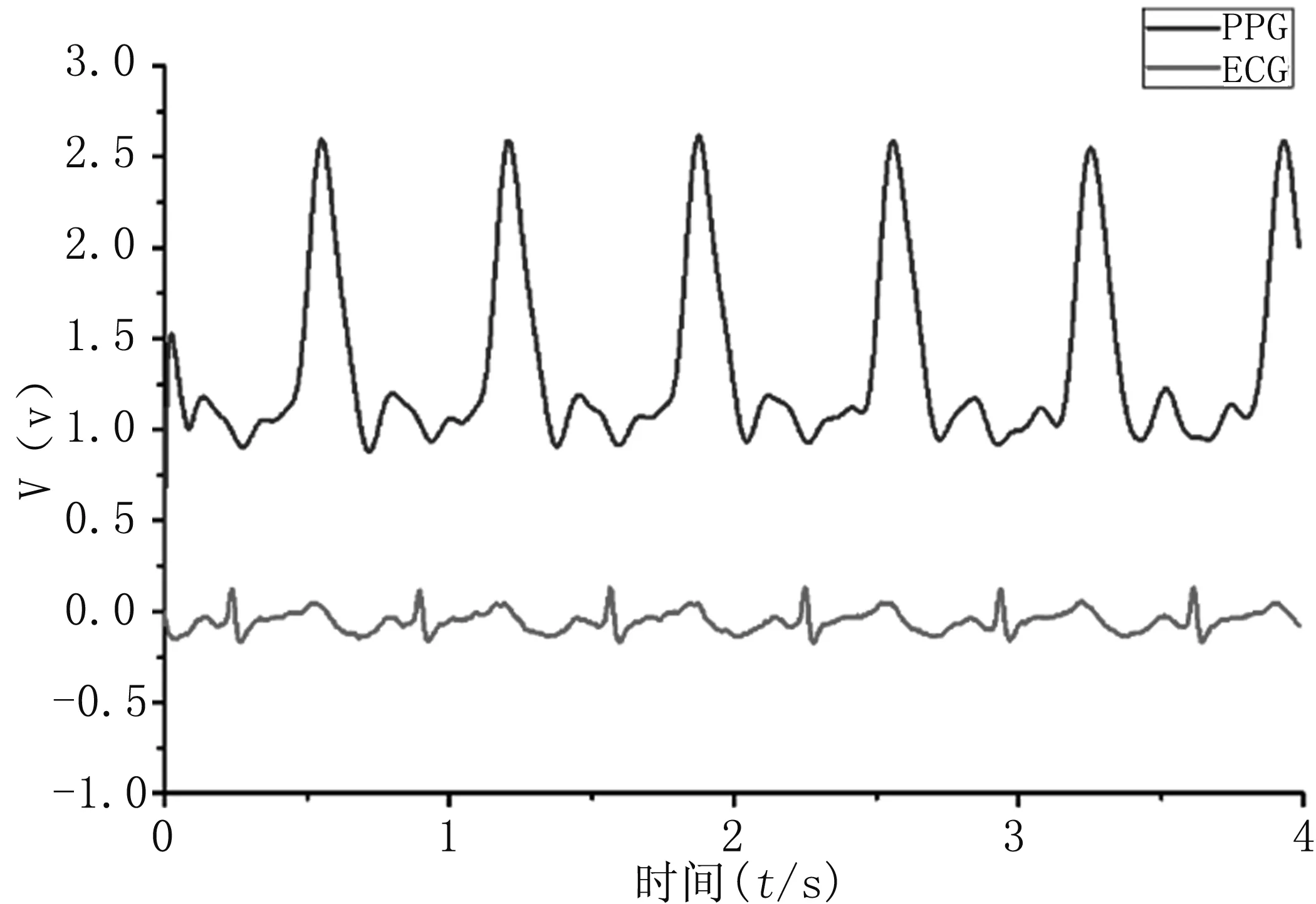
图3 滤波处理后的效果图
4 建模分析
利用Matlab计算200组数据的脉搏波传导时间以及脉搏波特征参数:脉搏波的传导时间(PTT)、脉搏波的波形系数(K’)、主波高度(H)、升支最大斜率(K)、每搏心输出量的特征参数(Z)、脉搏波的周期(T),各参数的范围见表1。
表1血压值及其相应的波形特征参数
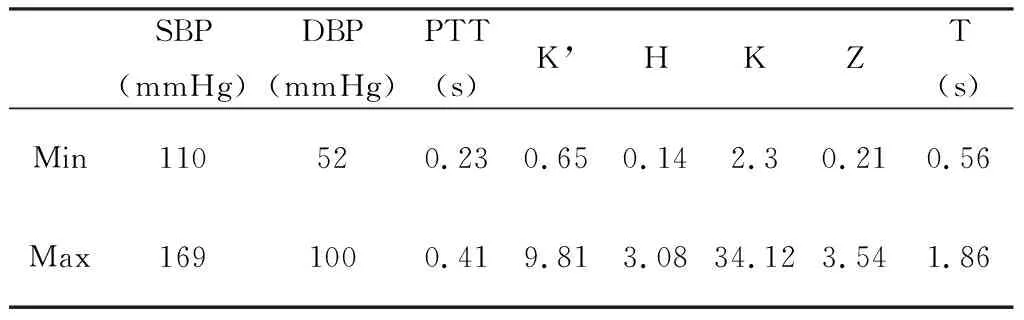
Table 1 The blood pressure value and the corresponding waveform characteristic parameters
对人体动脉收缩压(SBP)和舒张压(DBP)与脉搏波传导时间和脉搏波特征参数进行相关性分析,得到相关系数(R)见表2、3。
表2收缩压和脉搏波传导时间
以及脉搏特征参数的相关性分析结果
Table2Thesimplecorrelationanalysisofsystolicbloodpressureandpulsewaveconductiontimeandpulsecharacteristicparameters

相关系数PTTK’HKZTR-0.61-0.240.320.260.29-0.5
表3舒张压和脉搏波传导时间
以及脉搏特征参数的相关性分析结果
Table3Thesimplecorrelationanalysisofdiastolicbloodpressureandpulsewaveconductiontimeandpulsecharacteristicparameters

相关系数PTTK’HKZTR-0.63-0.410.400.390.42-0.58
从表2、表3可以看出,收缩压与舒张压均与脉搏波的传导时间、脉搏波的波形系数、主波高度、升支最大斜率、每搏心输出量的特征参数脉搏波的周期具有较好的相关性。
由图4可知,收缩压和舒张压预测值与实际测量值的相关性分别为0.76、0.80,线性关系良好,平均绝对误差分别为7.8、6.9 mmHg,满足AAMI国际电子血压计标准。
5 实验结果
为了验证其准确性,对5名新志愿者进行收缩压和舒张压测量,同时采集心电信号和脉搏波信号,利用Matlab对数据进行简单的处理,分析得出脉搏波传导时间和脉搏波特征参数,带入本研究建立的校正模型,实现对收缩压和舒张压的预测。计算结果和预测结果见表4。
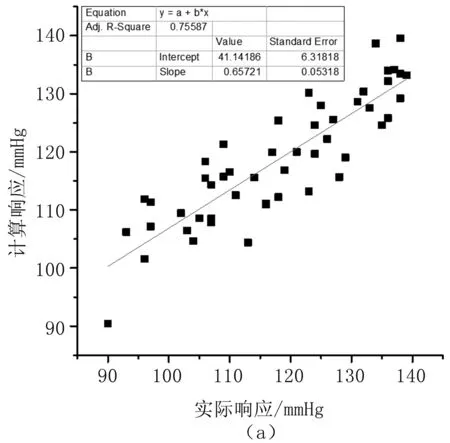
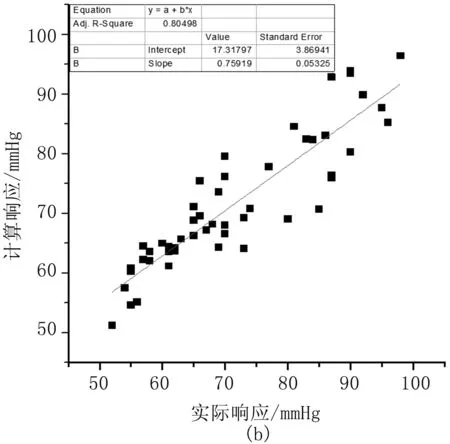
图4 测量值与计算值的对比
表4测试组PTT值、脉搏波特征值及血压预测结果
Table4ThebloodpressurepredictionresultsofPTTvalue,thecharacteristicsofpulsewave
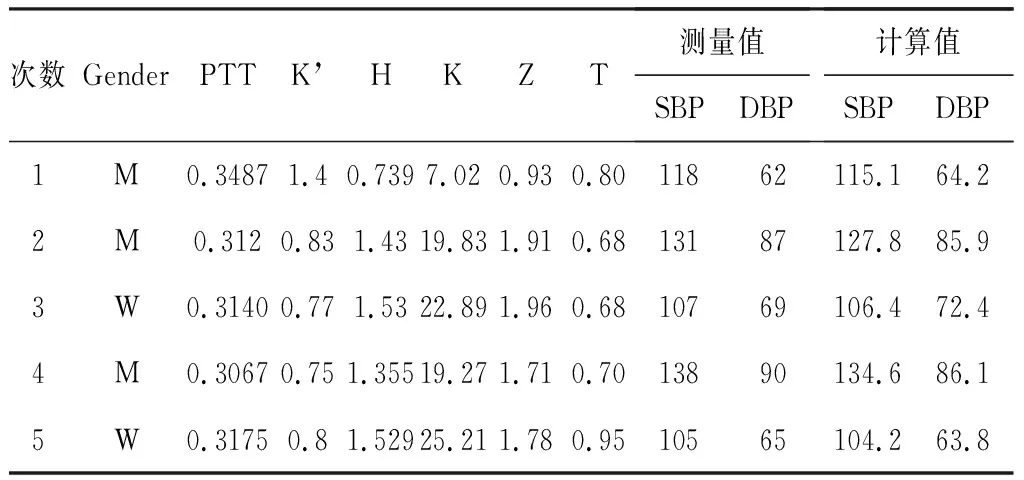
次数GenderPTTK’HKZT测量值SBPDBP计算值SBPDBP1M0.34871.40.7397.020.930.8011862115.164.22M0.3120.831.4319.831.910.6813187127.885.93W0.31400.771.5322.891.960.6810769106.472.44M0.30670.751.35519.271.710.7013890134.686.15W0.31750.81.52925.211.780.9510565104.263.8
图5为血压预测结果,其中SBP(a)为收缩压实际测量值,SBP(c)为收缩压计算值;DBP(a)为舒张压测量值,DBP(c)为舒张压计算值。预测平均绝对误差为5 mmHg之内,满足AAMI国际电子血压计标准。
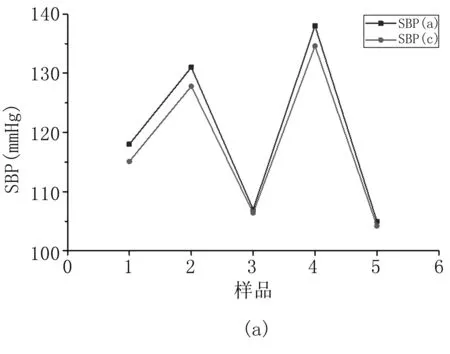
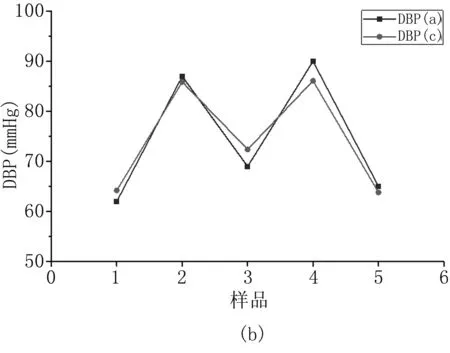
图5 测量值与计算值对比
6 结论
本研究提出了一种连续血压测量的新方法,利用偏最小二乘法分析脉搏波传导时间与脉搏波特征参数的关系,分别建立收缩压和舒张压与脉搏波传导时间PTT以及脉搏波特征参数的回归方程,以此实现血压的连续性、无袖带式检测。实验结果表明,该方法计算得到的舒张压和收缩压的预测平均绝对误差小于5 mmHg,满足AAMI[16]国际电子血压计标准要求。
