一种改进的条件方差和医学图像配准*

相艳，桂鹏，王硕，许春荣，邵党国，刘利军，汤守国

(昆明理工大学 信息工程与自动化学院，昆明 650051)

1 引 言

图像配准是指通过某种空间变换，能使两幅图像的特征点或者对应点在空间上达到一致。其中保持不动的图像称为参考图像，进行空间变换的称为浮动图像。图像配准一般由4个基本模块组成，即几何变换、图像插值、相似性测度和函数优化[1]。相似性测度衡量了参考图像和浮动图像匹配的程度。用于图像配准的相似性测度有相关法、最小化灰度差法、灰度比的方差最小化法、划分一致法、最小化联合熵方法和互信息法等，其中归一化互信息(normalized mutual information，NMI)被认为是配准精度和鲁棒性较好的回溯式配准方法之一[2]。但多模图像配准中NMI函数曲线容易出现局部极值，从而影响配准的精度和鲁棒性。交叉累计剩余熵(cross cumulative residual entropy，CCRE)使用累计剩余分布函数代替概率密度函数，能得到更光滑的配准目标函数[3]，近年来在多模图像配准中得到了很好的应用。但CCRE 需要计算分布函数，每次迭代时间较长，影响了配准效率[4]。Pickering 等人首次提出使用条件方差和(the sum of conditional variance，SCV)进行多模图像配准,使用高斯牛顿法求解量化后图像的SCV极小值，从而得到空间变换参数[5]。文献[6]的实验结果表明这种新的相似性测度与互信息相比，准确度和鲁棒性都有改善。此后，SCV更多被用于视觉追踪、视觉伺服[7-8]。

SCV的主要缺点是它仅使用参考和浮动图像的量化信息计算联合直方图[7]。本研究认为，在计算SCV的联合直方图时，就应该把浮动图像非网格点的插值方法结合进去，从而克服SCV的这个限制。浮动图像非网格点的插值对NMI、CCRE、SCV这些相似性测度曲线的光滑程度都有不同程度的影响。传统的插值方法有最近邻插值、线性插值、PV插值，这些插值方法明显缺陷是会产生插值伪影。插值伪影会产生局部极值，引起全局最优值的移动，从而给函数寻优带来困难，影响配准结果[9]。为了减少插值伪影，提高配准效率，新的插值方法不断涌现。其中一类方法是改变参与计算联合概率密度的邻域点范围，并使用改进的核函数来分配邻域点的权重，针对该类方法，Rohde等人通过频域分析指出，扩大邻域点范围、采用高阶的插值函数能从整体上降低局部极值的出现[10]。然而，随着插值函数阶次的增加，算法的复杂度也相应增加。为此，本研究设计了一种新的插值函数来替代高阶插值函数，从而提高现有SCV算法的性能。

实验结果表明，本研究方法在进行多模图像配准时，在保证准确度的同时，对空间变换较大和噪声较强的情况具有较好的鲁棒性，比NMI、CCRE和原SCV方法具有更高的配准成功率。

2 理论与方法2.1 SCV原理

参考图像和浮动图像的灰度值可以看作两个随机矩阵R、T(n×m)。令x=(x，y)为包含像素坐标的向量，(x，y)∈{1，2，…，m}×{1，2，…，n}，w(x，pa)是一个转换函数，其中空间变换参数pa将像素x从T(x)映射到R，x→w(x，pa)。参考图像和浮动图像之间的条件方差和计算公式为[11]：

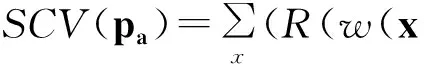
(1)

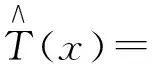
(2)

ε(·)表示数学期望运算。

2.2 改进的插值方法

当参数pa将像素x从T(x)映射到R时，该像素经过空间变换映射到参考图像中时通常为非网格点，而非网格点的空间插值方法会影响联合直方图的计算，从而影响SCV曲线的平滑程度，最终影响配准结果。常用的PV插值法是根据权重分配原则，将每对像素对联合直方图的贡献按权重分配给相邻的四个像素对。PV插值的一个缺陷是当插值点正好落在网格点处时，则该网格点处权重为1，而其他相邻的三个网格点权重为0，这会导致相似性测度容易在整数倍位移处出现局部极值。而改进的PV插值方法通过扩大邻域点范围，使用改进的插值函数来分配邻域点的权重。

以2D图像为例，设浮动图像上某点经空间变换后与参考图像的点q(非网格点)对应，点q的邻域点为qi(i=1，2，…，16)，见图1。p、q点对联合直方图贡献的概率计算如下：

h(T(p)，R(q))+=ωi，i=1，2，…，16

(3)

其中ωi为每个领域点qi的权重。

wi=f(dix)·f(diy)

(4)

上式中dix和diy为点qi(i=1，2，…，16)与q在x和y方向上的距离。

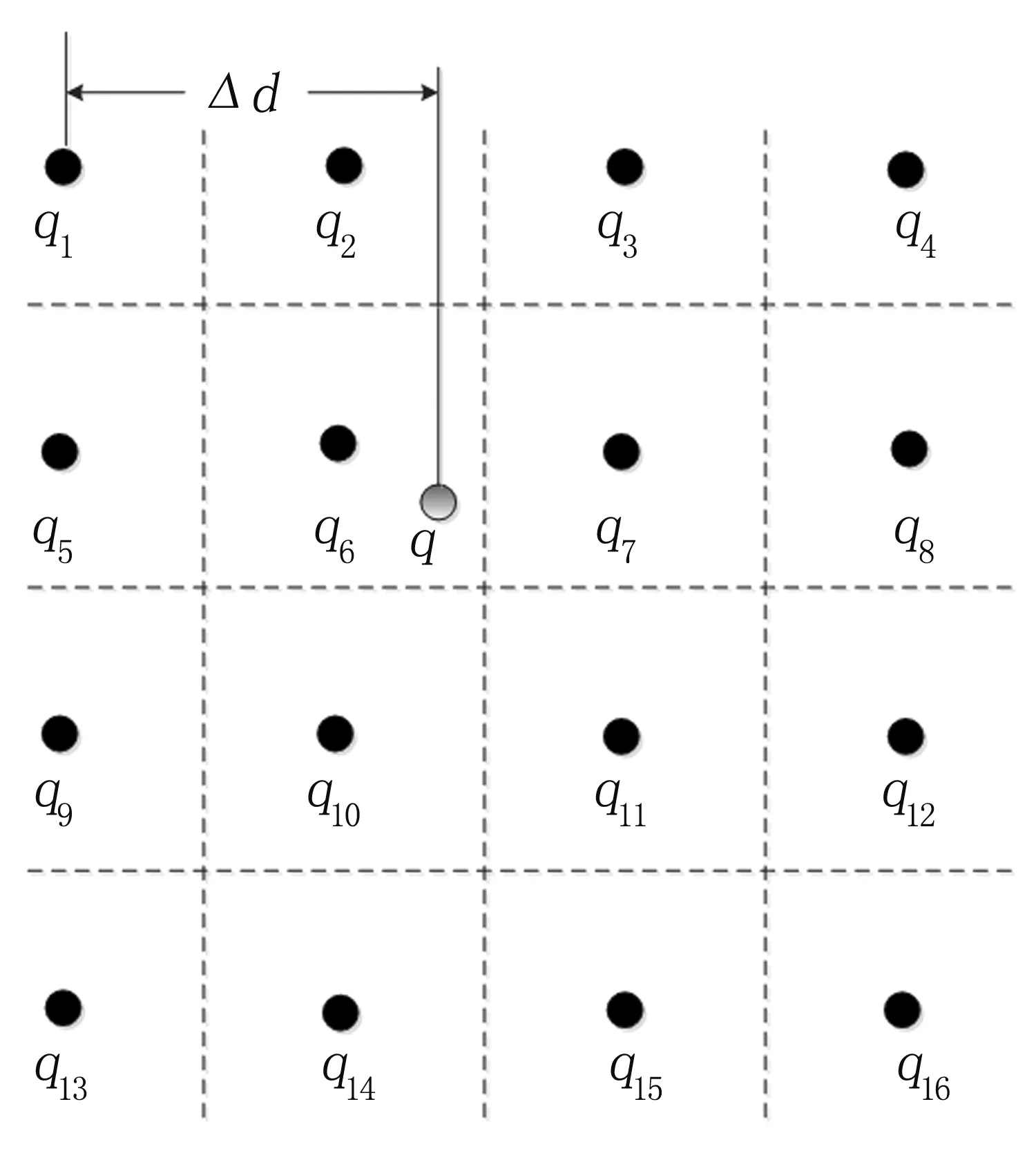
图1 改进的插值方法2D示意图

文献[12]指出，插值函数应该满足以下三个条件：

(1)f(x)≥0；

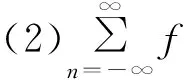
(3)f(x) 为单调递减函数。

本研究提出了一种满足上述三个条件的插值函数，具有如下形式：

(5)

如果令邻域点与插值点达到最大距离时不分配权重，即x=2时f(x)=0，则c=2。此时式(5)可简化为：

(6)

当点q落在非网格点上时，参与联合直方图统计的邻域点数目有16个；而当点q落在网格点q6上时，参与联合直方图统计的邻域点数目是最少的，有9 个。能分配到权重的最多邻域点数与最少邻域点数的比例为16:9，比传统PV插值法的比例4:1要小。该比例越小，说明联合直方图的概率分布越分散[12]，从而SCV出现局部极值的几率降低。

在计算邻域点权重时，上式中的公倍数1/4对邻域点的影响是相同的，因此可将其提出，公式(6)可以进一步简化为:

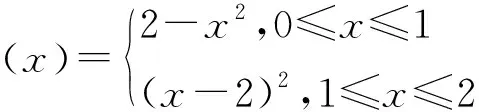
(7)

利用公式(7)计算插值函数的值，相当于在利用公式(6)计算出邻域点单个方向上的插值权重之后，再给每一个插值点权重都扩大4倍。因为这种变换是统一的线性比例变换，因此，不会改变公式(6)的权重分配，还能提高算法的效率。

2.3 本研究的相似性测度

本研究设计的相似性测度计算步骤如下：

(1) 对于寻优过程中给出的空间变换参数pa，将像素x从T(x)映射到R。根据映射至R中的插值点位置计算该点与其16个邻域点的距离，从而利用公式(7)计算出插值函数值，进一步利用公式(4)计算出每个邻域点的权重。

(2) 根据公式(3)计算出每一个插值点贡献给联合直方图的概率，从而得到参考图像和浮动图像的联合直方图，用H(u，v)表示，其中u表示参考图像的灰度，v表示浮动图像的灰度。u=1，2，…，dR；v=1，2，…dT，dR和dT是R和T的最大像素灰度级数目。

(3) 将公式(2)中的数学期望进一步展开为以下公式进行计算：

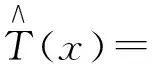
(8)

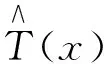
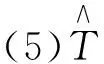
(9)

3 四种相似性测度曲线的比较

以BrainWeb数据集[13]中正常脑部磁共振T1加权第50断层图像为参考图像，见图2(a)，浮动图像为相应断层的PD加权像，见图2(b)。此外，图2(c)为根据公式(8)计算得到的浮动图像的期望值，图2(d)为图1(a)与(c)相减得到的图像,计算图2(d)中像素灰度的平方和，即得到(a)与(b)的SCV。

将图2(b)沿x轴及y轴平移-5～5像素，平移步长为0.1像素，计算其与图2(a)的NMI、CCRE、SCV以及本研究的相似性测度，得到见图3结果(SCV和本研究方法都取负值)。从图3中可以看出，NMI、CCRE、SCV在网格点位置都有不同程度的波动，其中NMI的局部极值最为明显，CCRE次之，SCV也有一定程度的波动，而本研究提出的方法最为平滑。NMI的抖动最为严重，极易使寻优陷入局部极值中，导致配准失败。本研究方法相比其他三种相似性测度，能保证优化算法顺利找到全局最值(最大或最小)，从而成功配准。

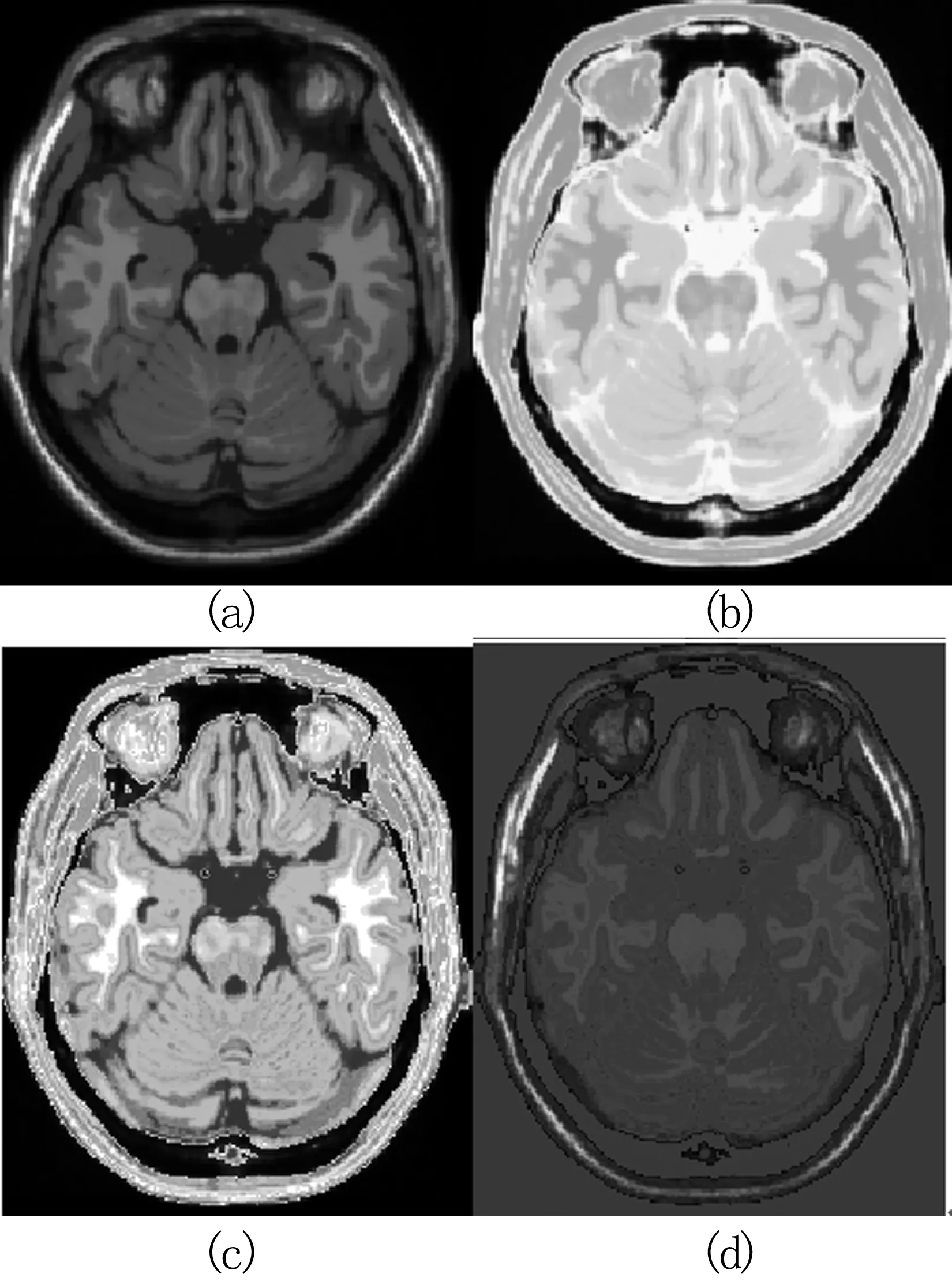
图2 实验所用的医学图像

4 多模图像配准实验

本研究分别针对多模图像配准中，空间变换范围不同或噪声强度不同时，四种相似性测度的表现进行测试，实验一针对的是空间变换范围不同的情况，参考图像为BrainWeb数据集中正常脑部磁共振T1加权第90断层图像，浮动图像为相应断层的T2加权像并做一定的刚体变换，设tx、ty分别为浮动图像沿x和y轴的平移，θ为绕图像中心点的顺时针旋转角度。在一定取值范围内随机选取三个参数的值，每一组测试中随机选取20个不同的刚体变换T=[tx，ty，θ]进行测试，其中第一组测试中tx、ty的绝对值范围为1～2，θ的绝对值范围为0～1；第二组中tx、ty的绝对值范围为14～15，θ的绝对值范围为2～3；第三组中tx、ty的绝对值范围加大至19～20，θ的绝对值范围为3～4,使用步长为5的Powell算法对NMI、CCRE、SCV和本研究方法相似性测度进行寻优，得到不同的配准参数T′=[tx′，ty′，θ′]，并与真实的参数T比较，求取与T的误差△T=[△tx，△ty，△θ]。如果寻优陷入局部极值，则配准失败。本研究中配准的性能评估采用以下公式计算：

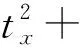
(10)

如果两幅图像完全配准，那么Err=0，如果Powell寻优陷入局部极值，则配准失败。图4为每组测试中20次配准的成功率。

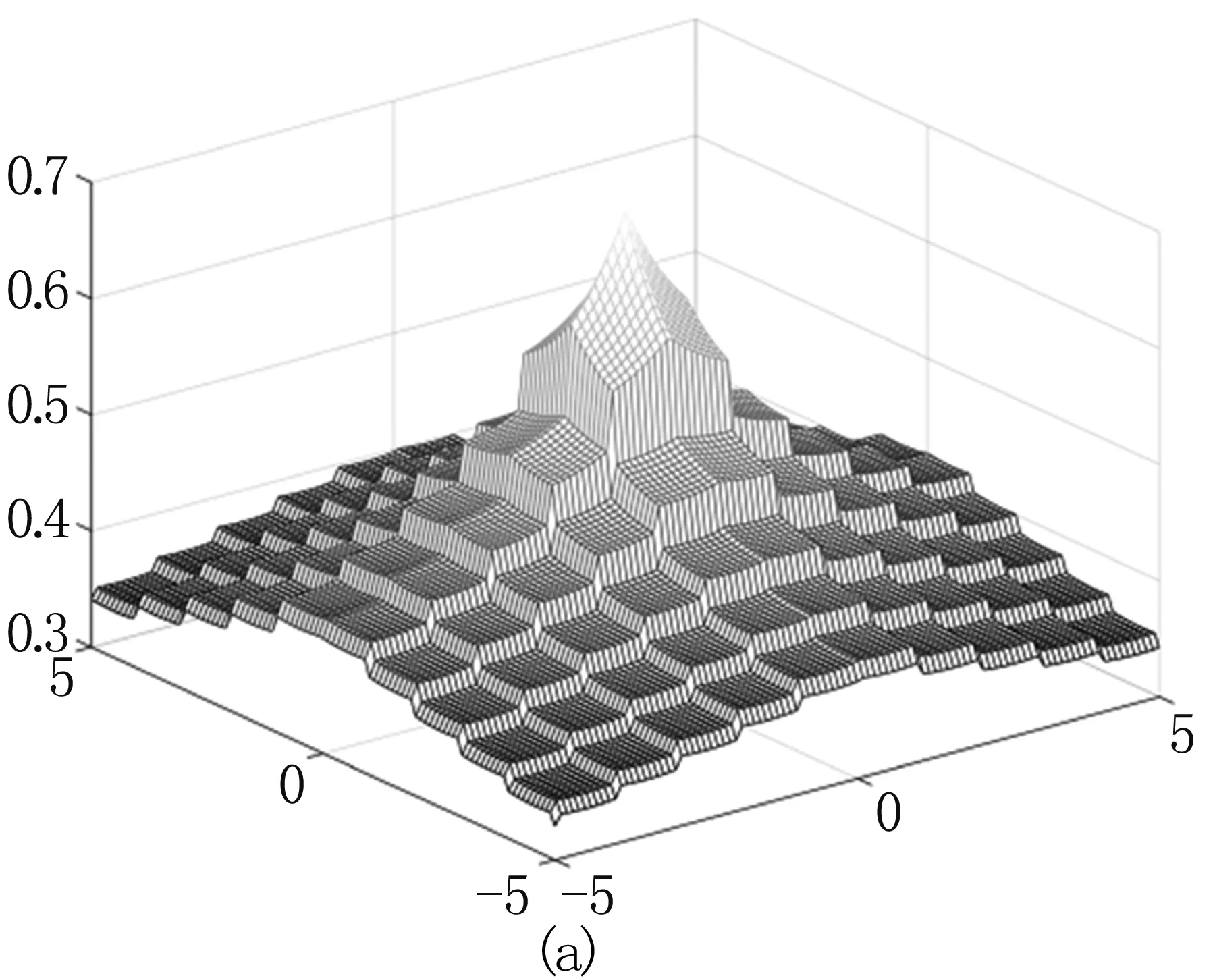
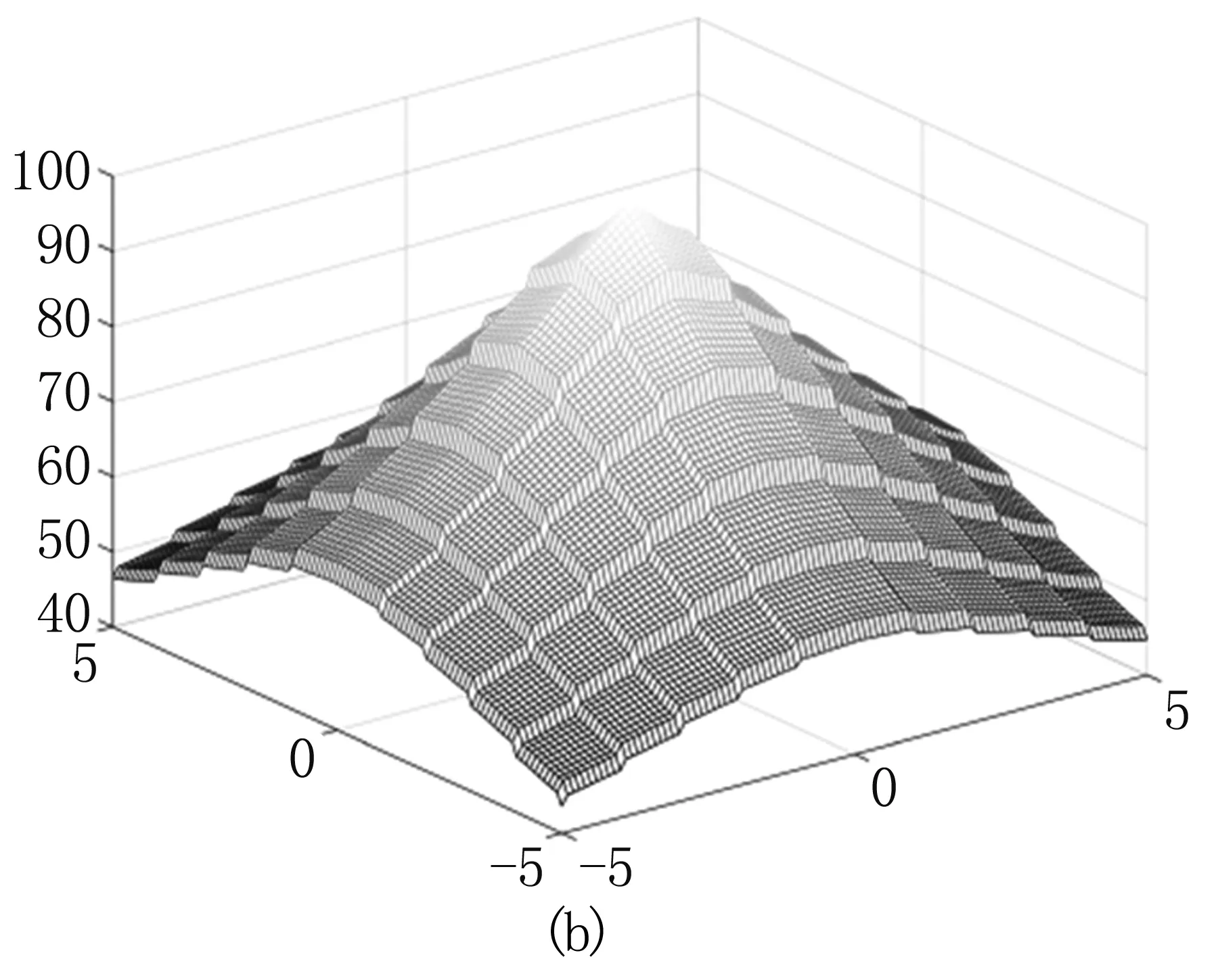
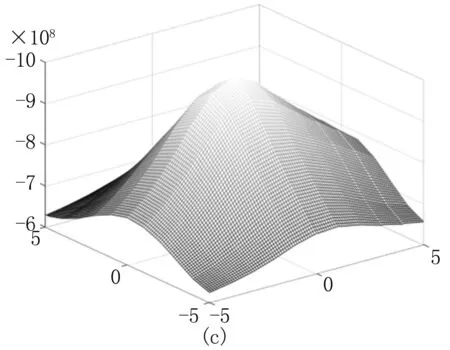
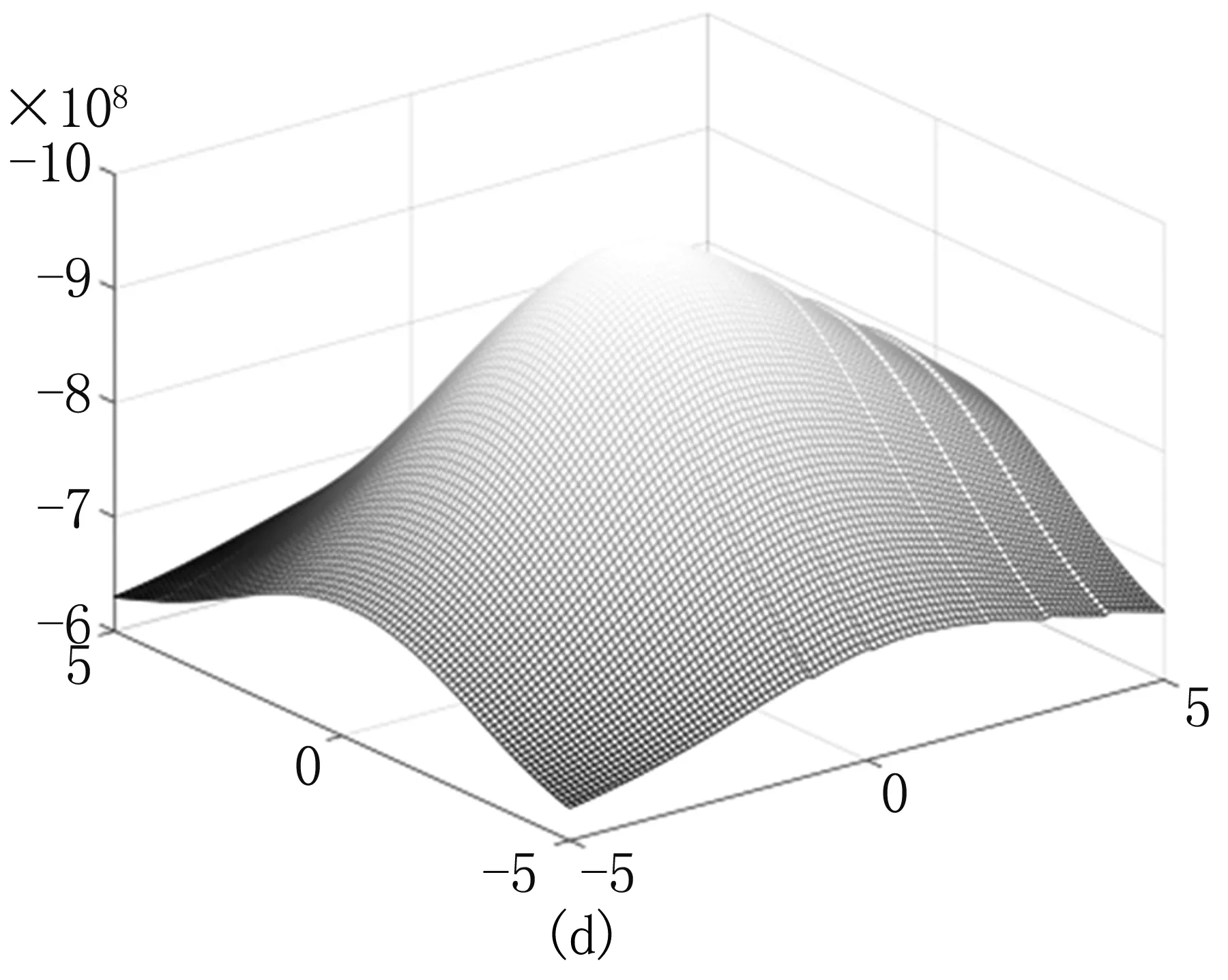
图3 NMI、CCRE、SCV和本研究的相似性测度

由上图可知，第一组测试中，当空间变换不大时， NMI、CCRE、SCV和本研究的方法成功率均达到了100%。第二组测试中，当空间变换加大时，本研究方法配准成功率为100%，SCV为89.47%，CCRE为89.47%，NMI为0。第三组测试中，本研究方法配准成功率为73.68%，SCV为57.89%，CCRE为68.42%，NMI为0。可以看出，当浮动图像相比参考图像的空间变化增加时，NMI、CCRE、SCV方法配准成功率都会降低，本研究提出的方法仍然可以达到较高的配准成功率。

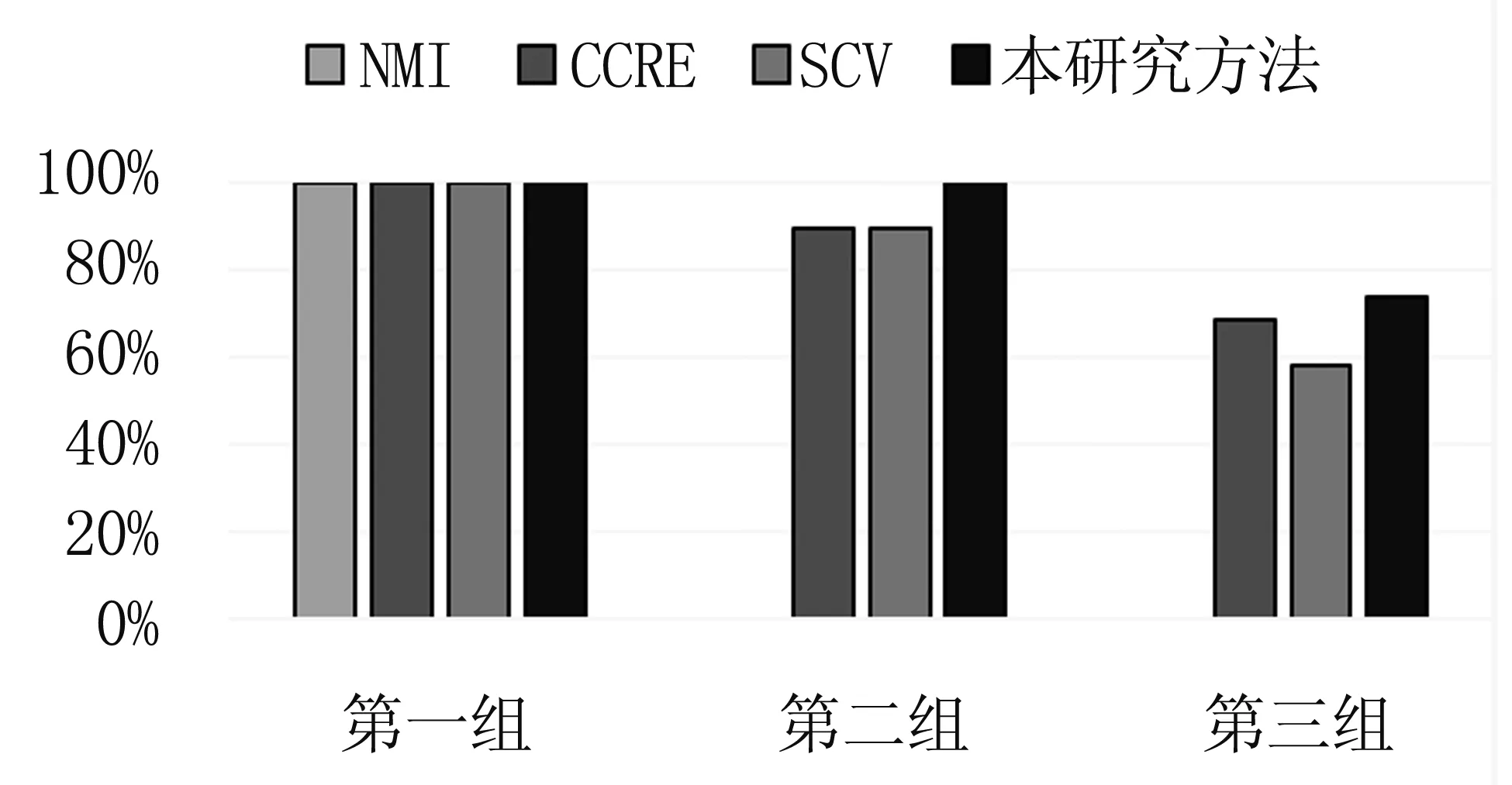
图4 实验一的配准结果

实验二针对的是噪声强度不同的情况。参考和浮动图像与实验一相同，但浮动图像做T=[9，9，2]的刚体变换。每一组测试中参考和浮动图像按照文献[14]的方法随机添加20次强度不同的的莱斯噪声。第四组测试的噪声标准差为14，第五组的噪声标准差为17，第六组的噪声标准差为19。图5为每组测试中20次配准的成功率。

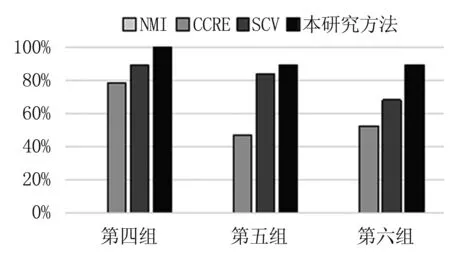
图5 实验二的配准结果

由图5可知，当空间变换大并有噪声存在时，NMI不能完成配准任务，配准率为0。第四组测试中本研究方法配准成功率为100%，SCV为89.47%，CCRE为78.95%。第五组测试中本研究方法配准成功率为89.45%，SCV为84.21%，CCRE为47.37%。第六组测试中本研究方法配准成功率为89.47%，SCV为68.42%，CCRE为52.63%。由图5可以看出，当噪声增大时，CCRE、SCV方法配准成功率都会降低，本研究提出的方法仍可达到较高的配准成功率。

表1列出以上六组测试中，成功配准得到的空间参数误差的平均值。

可以看出，本研究方法在保证配准成功率的同时，具有和其他方法一致甚至明显优于其他方法的配准精度。

表1配准精度

Table 1 Registering accuracy

5 结束语

在多模医学图像配准中，传统相似性测度曲线存在局部极值，为空间变换参数寻优带来困难。针对此问题，本研究提出一种改进的SCV作为相似性测度。实验表明，该方法与NMI、CCRE和原SCV相比有以下优点：(1)当参考图像和浮动图像的空间差别不大时，这四种相似性测度都能完成配准任务，而本研究方法精度最高。(2)当参考图像和浮动图像的空间差别较大或受到较大噪声干扰时，本研究方法的配准成功率最高。如前所述，本研究方法的相似性测度曲线较为光滑，从而提高配准的鲁棒性。(3)综合比较，本研究方法在保证了配准精度的同时对较大的空间变换和较强的噪声具有鲁棒性。该方法可以进一步扩展至3D医学图像配准中。今后将进一步研究该方法的3D配准应用。