基于高斯过程分步分类的阿尔茨海默病辅助诊断*
2018-10-18陈靖靳晨滕升华
陈靖,靳晨,滕升华
(山东科技大学电子通信与物理学院,青岛 266590)
1 引 言
阿尔茨海默病(alzheimer's disease,AD )是一种以脑功能衰退为特征的神经退行性疾病,是老年痴呆最常见的形式[1-2]。2015年根据国际相关组织报告,随着人口老龄化,AD发病率呈明显上升趋势,预计在现有AD患者的基础上,每20年增加1倍,估算到2050年将达到1亿人以上[3]。研究表明,及时诊断、发现AD前期阶段—轻度认知障碍(mild cognitive impairment,MCI)并进行相关治疗,可延缓甚至避免MCI发展恶化为AD,是防治AD的有效手段之一[4-5]。
到目前为止,已有多种生物标志物显示出对AD诊断的敏感性,从而众多分类方法被开发并应用于识别AD、MCI和健康对照组(healthy control,HC),其中支持向量机(support vector machine,SVM)对小样本学习操作简单且识别率高而被广泛应用,但处理高维脑影像数据其准确率并不能令人满意[4-9]。
高斯过程分类(gaussian process classification,GPC)是一种基于概率判别和核函数的贝叶斯机器学习方法,其分类思想是假设映射函数服从均值为协方差矩阵(即核函数)为K的高斯分布先验,然后通过贝叶斯推理获得合适的,使之能够对测试样本类别进行概率预测[10-11]。GPC在识别分类研究中展现出良好的性能,Bazi把GPC应用到遥感图像的分类上,比较了在不同的核函数和近似方法下的分类结果,同时在与SVM的精度比较上取得了更好的结果[12];Chen将GPC和深度信念网络结合,应用于音乐情感检测系统,结果显示性能良好[13];黄维在人脸识别分类中使用GPC,并成功解决了多分类问题[14];耿雪青将GPC应用于运动想象脑电信号分类,并与SVM分类进行比较,证明了该方法的有效性[15]。
对AD分类的研究,可供使用的有标记脑影像数据仍然相对较少。利用GPC解决有监督分类问题,训练样本数量是影响识别率的一个重要因素,若样本数量不足可能会造成类内协方差矩阵奇异或者协方差矩阵的逆阵不稳定,使得映射函数的后验概率参数无法进行估计,除此之外,小样本问题还会使结果产生较大的偶然性。为了缓解训练样本数量少的问题,可以采用无标记样本参与训练。一种做法是半监督分类[16],即用部分未标记数据和标记数据联合进行模式分析,但算法通常较为复杂。本研究设计一种分步的分类模式:先进行一次高斯过程分类,把分类结果确定性强的测试样本作为补充参与训练,以此增加训练样本数量;再对后验概率差异较小、容易造成错分的样本进行二次分类。利用更多的训练样本能更准确地在特征空间表征对应的分类模式,进而提升分类性能。最后,通过实验验证了该方法对AD辅助诊断的有效性。
2 算法
2.1 常规高斯过程分类算法
GPC相对于神经网络和SVM等分类方法的优势首先体现在采用概率模型,模型输出值为测试样本属于每一类的概率数据而不是预测的标签,这一点在临床诊断中更有意义。其次GPC不需要手动设置模型参数,这些参数都是在应用高斯函数求解后验概率时自动获取的。此外,参数相对较少,优化参数和进行收敛则更简单。
GPC包含3个模块:定义映射函数(隐变量函数)、定义似然函数、计算映射函数的后验概率。
在分类问题中似然函数通常定义为一个S形函数,不能直接得到映射函数的后验概率,通常利用高斯函数来逼近后验概率,主要包括Kullback-Leibler散度最小化、期望传播(Expectation Propagation)、Laplace逼近、Markov Chain Monte Carlo方法等[10]。
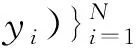
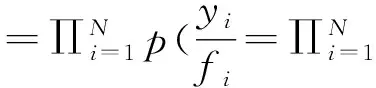
(1)
假设映射函数服从均值为零、协方差矩阵为平方指数协方差核函数(RBF)的多维高斯过程分布,则先验概率p(f/x)表示为:
p(f/x)=N(0,K)
(2)
式中,K为协方差矩阵,由贝叶斯定理可得映射函数的后验概率为:
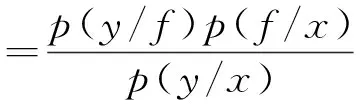
(3)
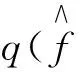
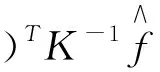
(4)
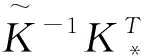
(5)
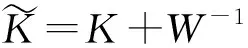
则对于测试样本x*输出为正样本的概率为:
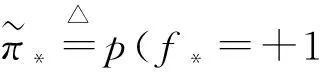
(6)
2.2 高斯过程分步分类
对于AD诊断常用高维脑影像数据,训练样本数量相对较少,直接利用GPC的准确率较低。观察样本从属于正样本的概率,有些数值非常高甚至接近于1、或者非常低而近似于0,对这些样本进行类别判定通常不会产生错误。更进一步,把这些易分样本筛选出来与原有训练数据合并作为新的训练样本,可看作增加了训练样本的数量,从而有可能改善分类性能。这就是高斯过程分步分类(gaussian process stepwise classification, GPSC)的基本思想,处理流程见图1。具体地,先将测试样本进行一次高斯过程分类,得到测试样本对应于每一类的预测概率。当类别之间的预测概率相差不大时,说明该样本的特征不明显,容易造成错分,如两类问题、预测概率近似为0.5。确定模糊概率范围,把预测概率位于此范围内的样本定为易错样本,其他样本为易识别样本。在第二步分类中,将易识别样本作为补充参与训练,对易错样本重新进行分类,从而得到这部分样本最终的判定结果。
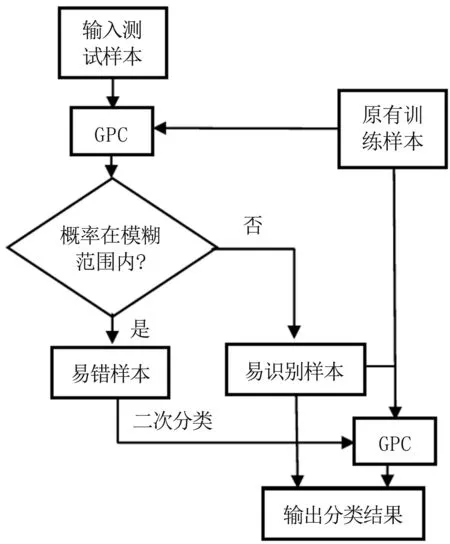
图1 高斯过程分步分类流程图
3 实验结果及分析
实验数据采用(alzheimer’s disease neuroimaging initiative,ADNI) 数据库的磁共振影像(magnetic resonance imaging, MRI)。所用MRI均采用1.5T扫描,对MR图像进行灰度校正和配准,并把大脑分成93个感兴趣区域[18],将每个区域的灰质体积作为样本特征。
实验中共使用807个样本:AD样本为186个,HC样本为226个,MCI样本395个,包括167个进展型MCI样本(progressive MCI, pMCI)和228个稳定型MCI样本(stable MCI, sMCI)。为了验证GPSC算法的有效性,实验将GPSC算法与SVM、GPC两种分类方法进行比较。
GPC的输出结果为测试样本属于每一类的概率值,通过设定阈值判定类别归属;阈值不同,分类灵敏度和特异度也会发生相应的变化,可根据实际需要对灵敏度和特异度进行调节,这也是高斯过程分类方法一个优良特性。为公平比较GPC和GPSC的分类性能,实验中阈值均取0.5,并通过十折交叉验证计算分类指标,具体包括准确率、灵敏度、特异度和ROC曲线下面积(area under curve, AUC)。
3.1 AD vs. HC分类
实验数据是186个AD样本和226个HC样本。SVM、GPC和GPSC等三种分类方法的识别结果见表1,ROC曲线见图2。
表1三种方法对ADvs.HC的分类结果
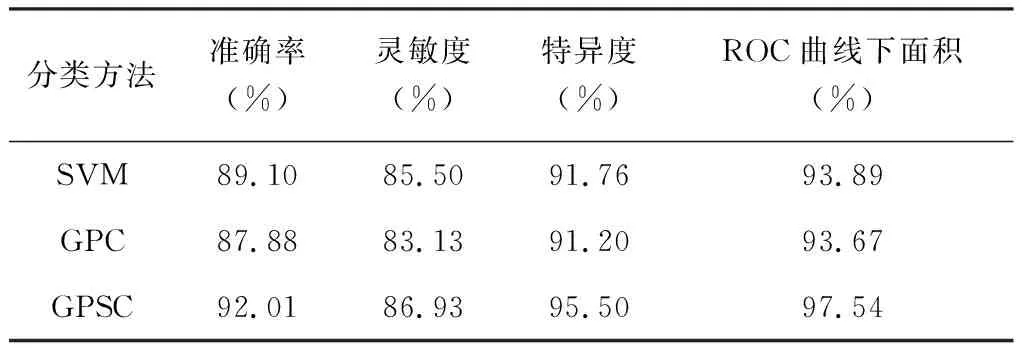
Table 1 Classification results of three methods for AD vs. HC
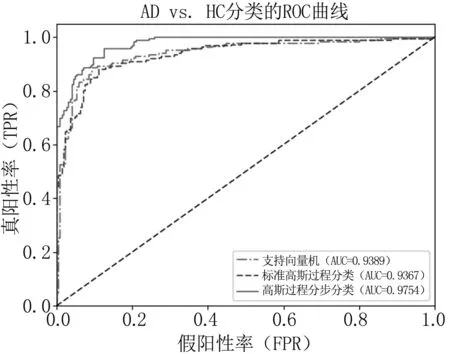
图2 三种方法对AD vs. HC分类的ROC曲线
可以看出,与SVM和GPC相比,GPSC能显著提升分类的准确率、灵敏度、特异度以及AUC值。与此对应,图2所示ROC曲线同样表明GPSC综合性能最优。
3.2 MCI vs. HC分类
本次实验数据为395个MCI样本,其中包括167个pMCI样本和228个sMCI样本,以及226个HC样本。GPSC和SVM、GPC三种分类方法的识别结果见表2,ROC曲线见图3。
表2三种方法对MCIvs.HC的分类结果

Table 2 Classification results of three methods for MCI vs. HC
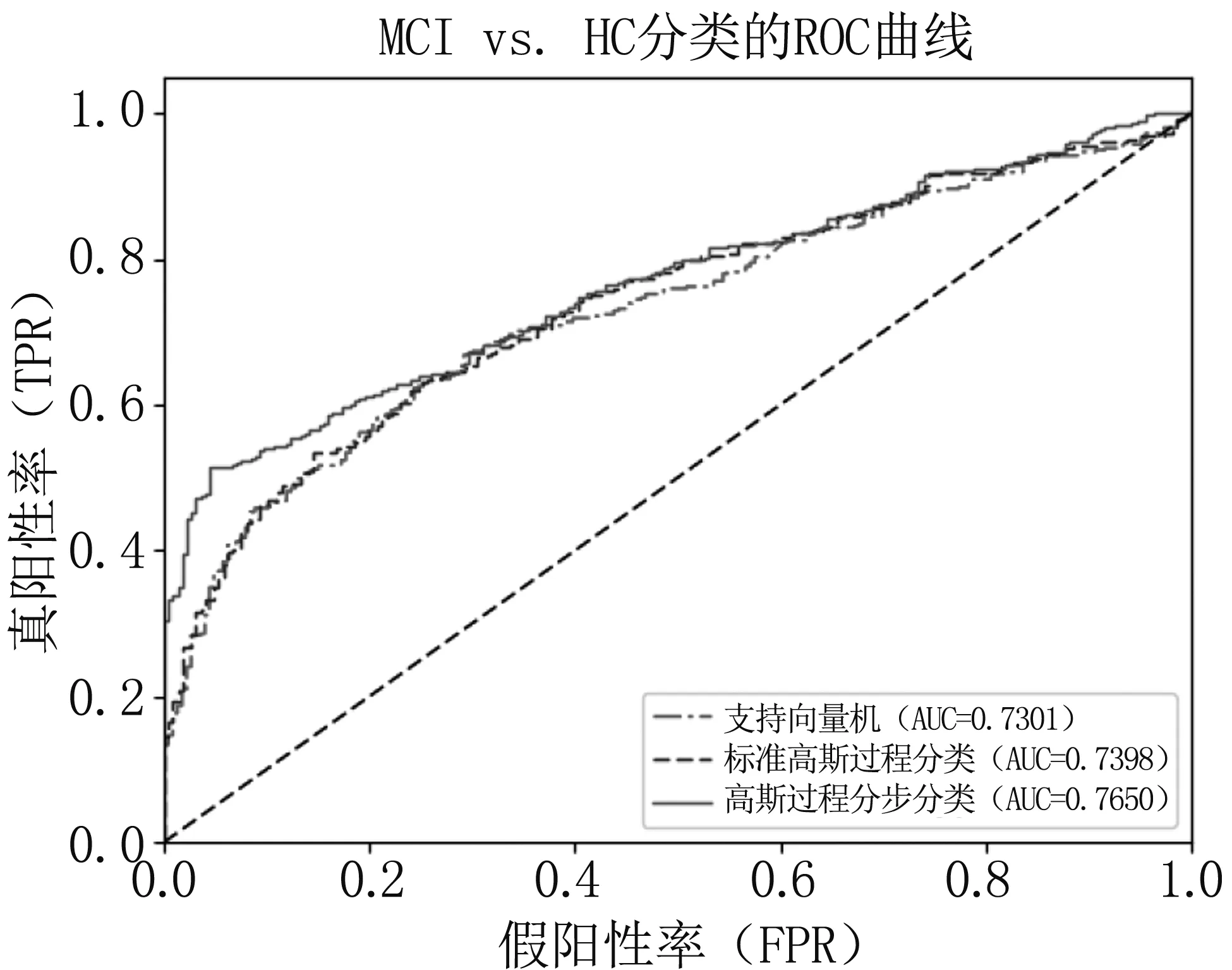
图3 三种方法对MCI vs. HC分类的ROC曲线
从表2可以看出,实验结果和AD vs. HC分类结果一致,GPSC分类性能相对于其他两种分类方法都是最好的。结合图3的ROC曲线,再次证明GPSC分类性能最优。
3.3 pMCI vs. sMCI分类
为充分验证GPSC算法的有效性以及对MCI病情转化预测的准确性,本次实验数据采用167个pMCI样本和228个sMCI样本,两类样本的区别为是否在18个月内转为AD患者,若转为AD患者,则为进展型MCI即pMCI,反之为sMCI。GPSC和SVM、GPC三种分类方法的识别结果见表3,图4是相应的ROC曲线。
表3三种方法对pMCIvs.sMCI的分类结果
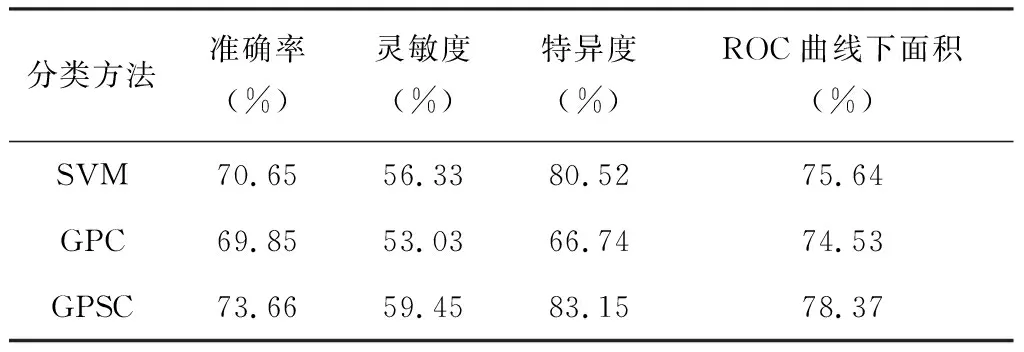
Table 3 Classification results of three methods for pMCI vs. sMCI
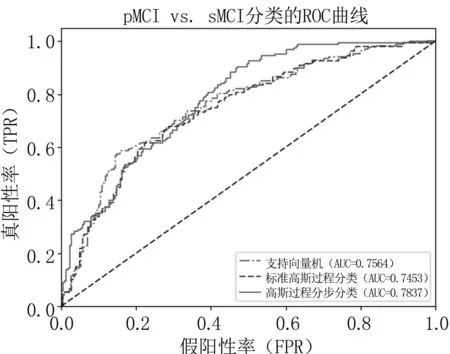
图4三种方法对pMCIvs.sMCI分类的ROC曲线
Fig4ROCcurvesoffourmethodsfor
pMCIvs.sMCIclassification
从表3可以看出,GPSC对于病变特征相似且不符合老年痴呆诊断标准的pMCI和sMCI样本依然具有分类能力,准确率、灵敏度、特异度以及AUC值同样高于其他两种分类方法,图4的ROC曲线也证明了GPSC算法的有效性。
4 结论
受限于数据的高维度和有限的训练样本数量,常规高斯过程分类和SVM在对结构性脑影像数据进行分类时的准确率不是非常理想。本研究提出基于分步分类模式的高斯过程分步分类方法:先对测试样本进行一次高斯过程分类,根据预测概率是否在模糊范围内,将测试样本分为易错样本和易识别样本;在第二次分类中,将易识别样本作为补充参与训练,以此增加训练样本数量,并对易错样本进行第二次分类。
将高斯过程分步分类应用于AD诊断,通过对AD vs. HC、MCI vs. HC、pMCI vs. sMCI分类的结果表明,高斯过程分步分类的分类性能要优于常规高斯过程分类和SVM分类。
为验证高斯过程分步分类方法对AD诊断的有效性,本研究仅利用了结构性磁共振脑影像数据;后续工作将加入FDG-PET等其他模态数据,以进一步提高对阿尔茨海默病计算机辅助诊断的性能。
