7075-T651铝合金薄壁管件多轴低周疲劳行为及寿命预测

陈亚军，刘辰辰，褚玉龙，宋肖肖

(1 中国民航大学 中欧航空工程师学院，天津 300300； 2 中国航发上海商用航空发动机制造有限责任公司，上海 201306)

7075铝合金作为硬铝合金的一种，具有较高的比强度和硬度、较好的耐腐蚀性能和较高的韧性[1]，作为飞机结构材料，可用于制造蒙皮、翼梁、隔框、起落架及液压系统零部件等，被广泛应用于航空领域[2-3]。在服役过程中，飞机结构常常受到多轴疲劳载荷的作用，对材料的失效行为及机理进行分析至关重要[4-7]。

加载条件往往会对疲劳寿命产生影响[8-9]，赵凯等[10]对弹簧钢进行比例加载条件下的多轴疲劳实验，发现弯曲应力占等效应力的比值对寿命有显著作用。Zhang 等[11]利用2A12铝合金进行多轴高周疲劳实验，指出载荷高低会影响断裂形式，多轴加载常常形成混合型裂纹。Zhao等[12]对7075铝合金进行了不同加载条件下的单轴和多轴疲劳实验，发现轴向平均应力降低了材料疲劳强度。断裂形貌会受到加载条件的影响，对其进行分析可得失效形式和机理。韩剑等[13]利用7075-T651铝合金棒材进行拉压疲劳实验，发现裂纹源的产生有两种原因，一是生产和加工过程中产生的缺陷，二是夹杂的第二相颗粒与基体脱离。Jo等[14]对渗碳钢进行多轴疲劳实验，发现裂纹萌生于试样亚表面。陈涛等[15]对7075-T651铝合金的单轴疲劳断口进行分析，发现其主要断裂形式为微孔聚集韧窝型，且不同应力幅下的位错形态不同。

相对于单轴疲劳而言，多轴加载条件下的寿命预测更为复杂[16-17]。根据选取损伤参量和疲劳参数的不同，可以将多轴疲劳寿命预测准则分为4类，即应力准则、应变准则、能量准则和临界面准则[18-19]。Gough等[20]给出了椭圆方程应力准则，Lee等[21]考虑载荷间的相位差对其进行了修正。崔云等[22]将非比例度引入Basquin准则，预测AZ31镁合金多轴低周疲劳寿命。陈旭等[23]考虑附加强化提出基于应变参量的低周疲劳判据，Ellyin[24]利用总应变能密度预测疲劳寿命。临界平面法通过选取疲劳过程中特定平面的特征参数进行寿命预测，如最大正应力[25]、剪切应变[26]以及应力应变的乘积[27]等，但作为一种时域分析手段，疲劳过程中的计算较为复杂，因此，也有通过频域分析进行寿命预测的相关研究[28]。

目前，有关7075铝合金疲劳行为的研究，主要集中在单轴疲劳方面，关于加载条件对7075铝合金多轴疲劳性能影响的研究报道较少。本工作通过对7075-T651铝合金薄壁管件进行以等效应力幅、应力幅比和拉扭相位差作为变量的多轴疲劳实验，研究不同加载条件对多轴疲劳寿命的影响，分析疲劳过程曲线，结合宏观和微观断口形貌分析，对薄壁管件多轴疲劳失效机理进行探究，并提出改进的Basquin准则，对不同加载条件下的多轴疲劳寿命进行预测。

1 实验材料与方法

1.1 试样材料和尺寸

实验所用7075-T651铝合金化学成分如表1所示，采用挤压成型、直径为30mm的圆棒材，沿成型方向取材加工试样，测得材料常温下的基本力学性能为：屈服强度492.95MPa，抗拉强度538.90MPa，弹性模量70.36GPa。对于多轴疲劳实验，依照美国材料测试标准ASTME2207加工成薄壁管状试样，尺寸如图1所示。

表1 7075-T651铝合金化学成分(质量分数/%)Table 1 Chemical compositions of 7075-T651 aluminum alloy (mass fraction/%)

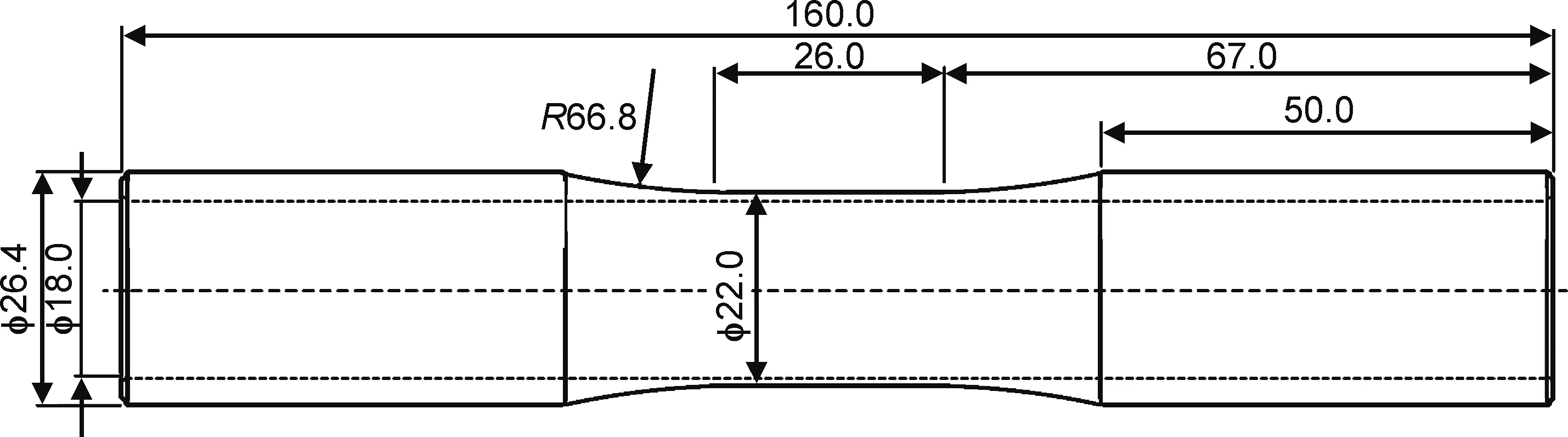
图1 疲劳管件试样尺寸图Fig.1 Tubular specimen geometry for fatigue tests

1.2 实验方法

利用SDN100/1000电液伺服拉扭复合疲劳试验机进行拉扭双通道应力控制的多轴疲劳实验，轴向和扭向的应力根据von Mises准则进行确定，表达式见式(1)：

(1)

其中:σeq为von Mises等效应力;σ为轴向应力；τ为扭转剪切应力。实验中均采取频率为5Hz的正弦波形加载，式(2)和式(3)分别为轴向应力和扭转剪切应力的表达式：

σ=σasinωt

(2)

τ=τasin(ωt-φ)

(3)

式中：σa为轴向应力幅；τa为扭转剪切应力幅；ω为加载角频率；t为加载时间；φ为轴向和扭转剪切应力之间的相位差。轴向应力和扭转剪切应力的关系通过应力幅比λ=σa/τa表示。分别选取不同的等效应力幅、应力幅比和拉扭相位差进行实验，具体加载条件如表2所示。图2给出了应力幅比和拉扭相位差变量实验的加载路径。实验在室温大气环境下进行，对于每种加载条件，均进行5次重复实验。试样断裂后将疲劳断口切下进行超声波清洗，利用Hitachi S-3400N扫描电子显微镜进行断口形貌观察，分析多轴疲劳断裂机理。

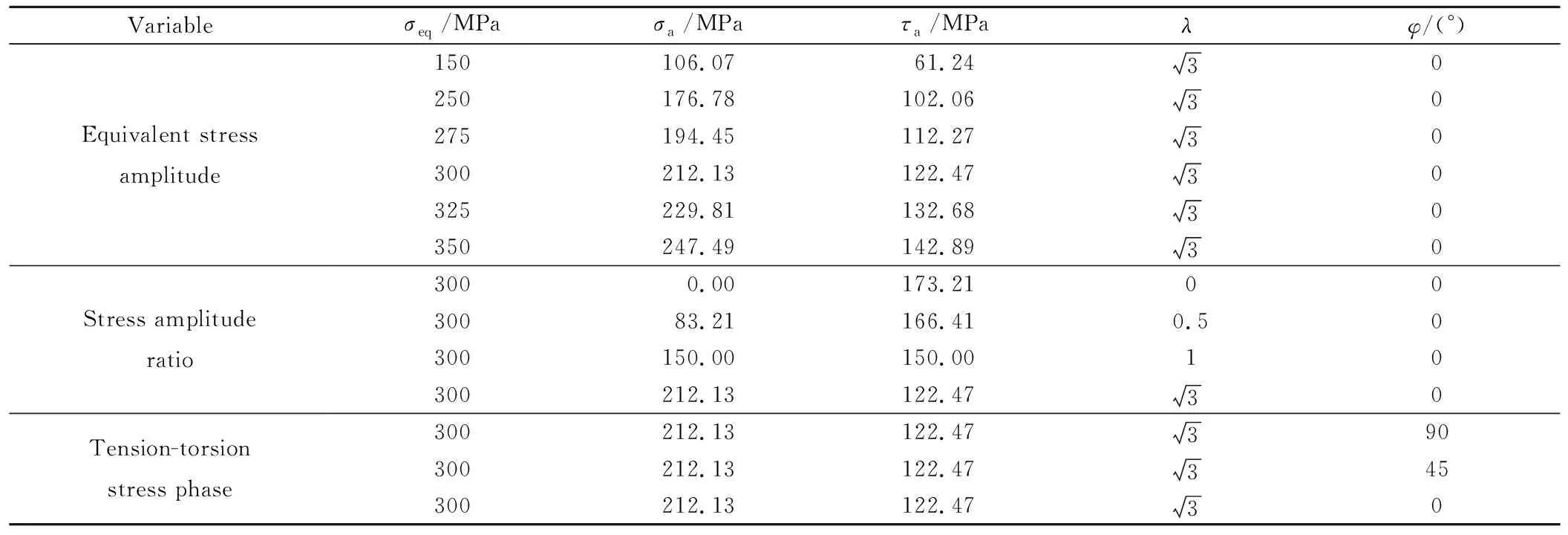
表2 多轴疲劳实验加载参数Table 2 Loading parameters of multiaxial fatigue tests

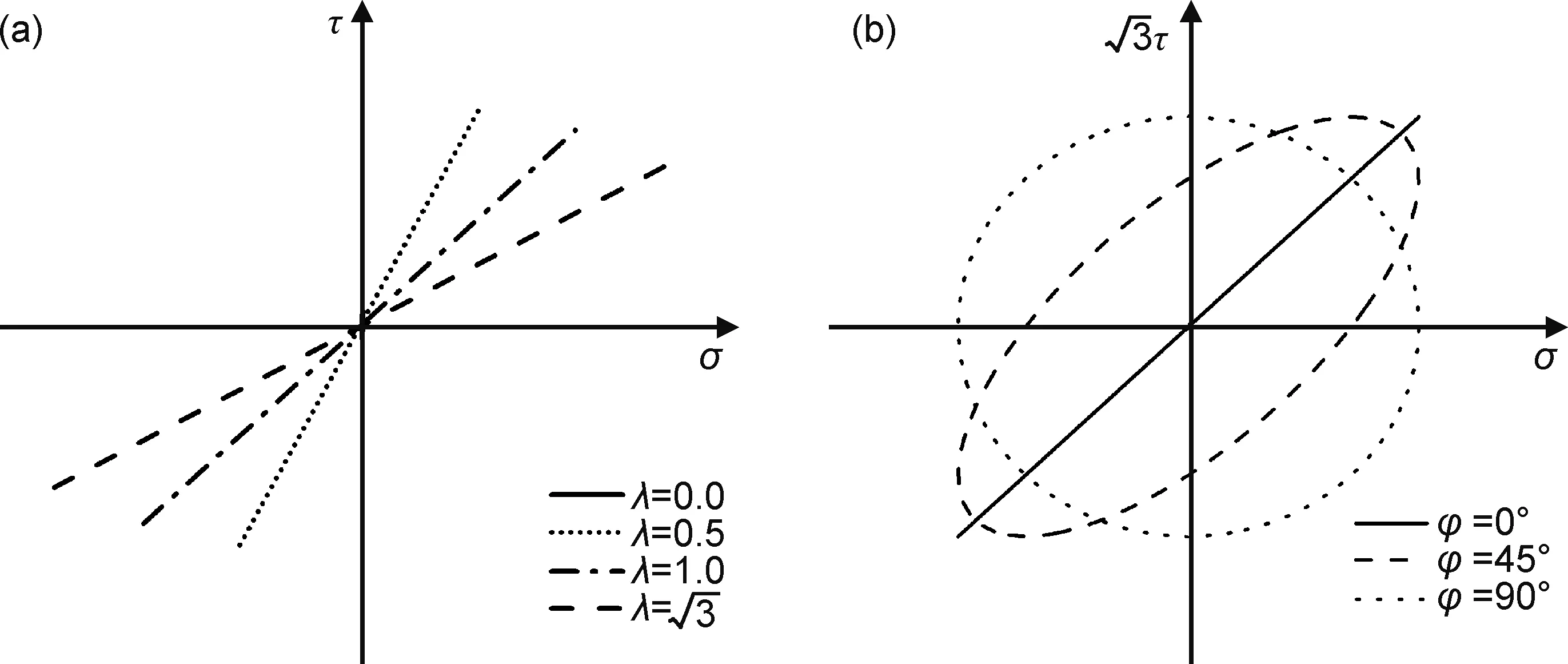
图2 多轴疲劳实验的加载路径 (a)应力幅比变量；(b)拉扭相位差变量Fig.2 Loading path of multiaxial fatigue tests (a)stress ratio amplitude variable;(b)tension-torsion stress phase variable

2 多轴疲劳行为

2.1 寿命规律和加载曲线

2.1.1 实验结果

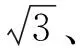
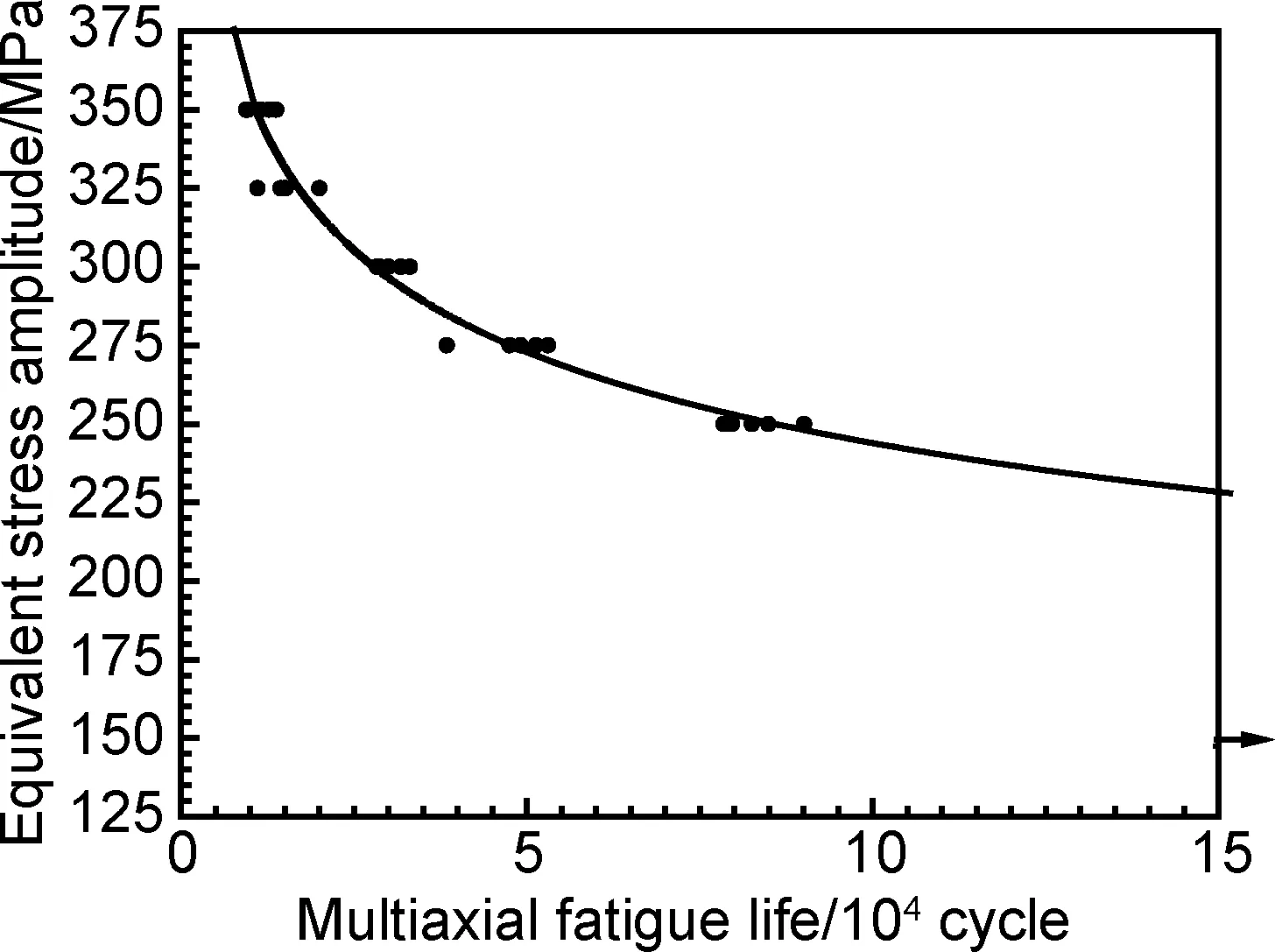
图3 应力幅比λ为相位差φ为0°时等效应力幅和多轴疲劳寿命的关系Fig.3 Relation between equivalent stress amplitude and multiaxial fatigue life with and φ= 0°

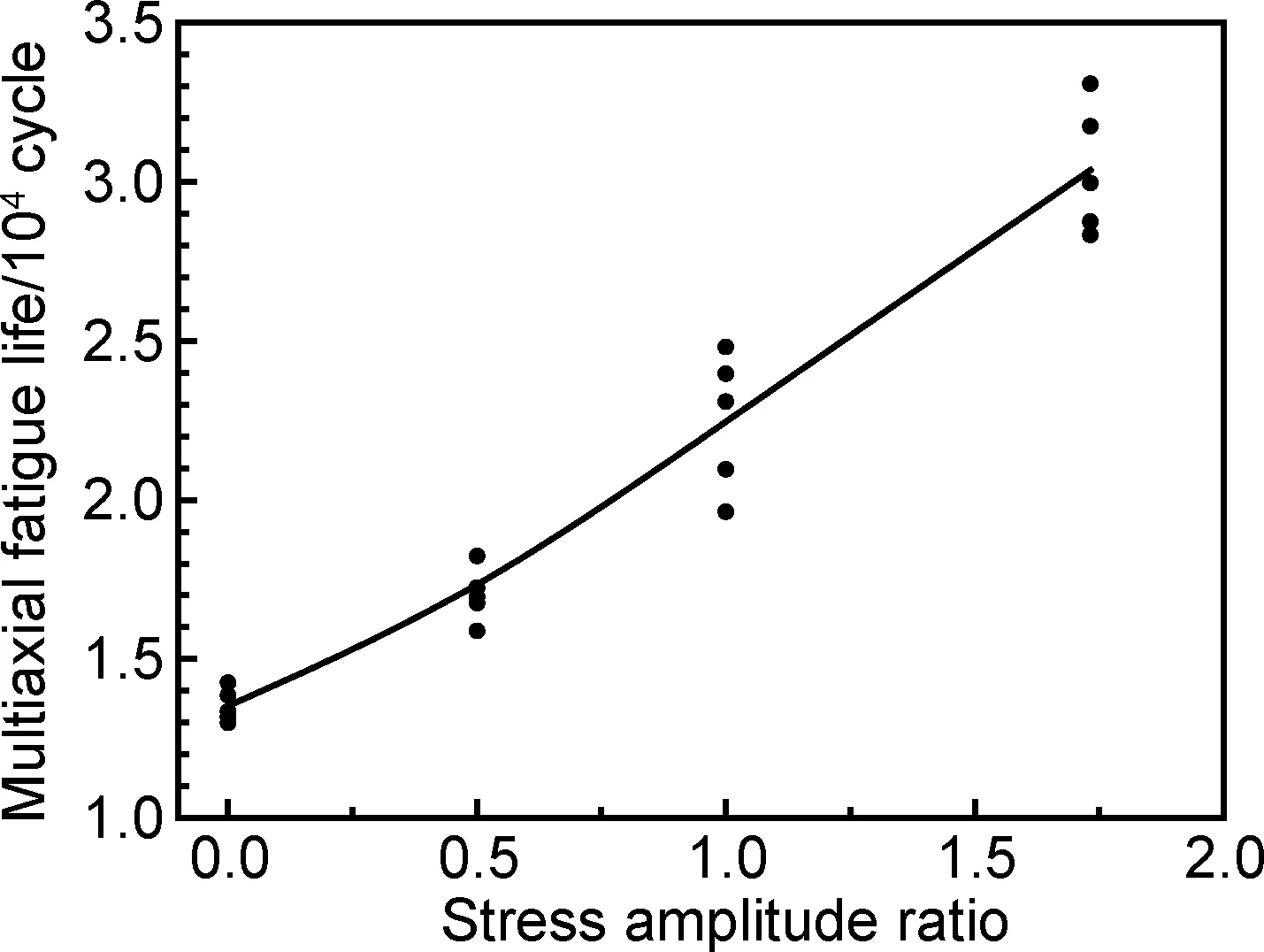
图4 等效应力幅σeq为300MPa、相位差φ为0°时应力幅比和多轴疲劳寿命的关系Fig.4 Relation between stress amplitude ratio and multiaxial fatigue life with σeq= 300MPa and φ= 0°

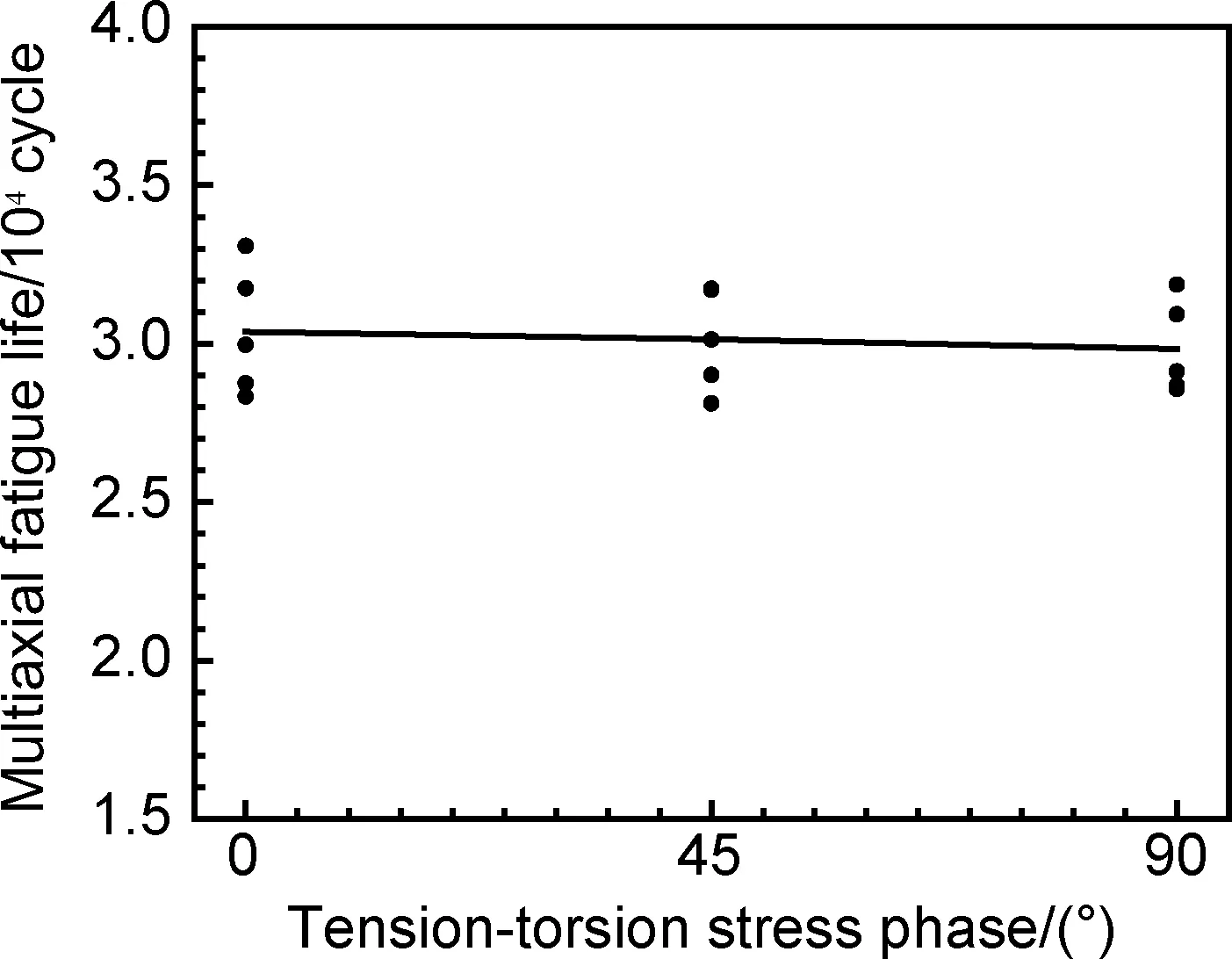
图5 等效应力幅σeq为300MPa、应力幅比λ为时拉扭相位差和多轴疲劳寿命的关系Fig.5 Relation between tension-torsion stress phase and multiaxial fatigue life with σeq= 300MPa and λ=

2.1.2 加载曲线分析

多轴疲劳实验过程中，加载稳定后每隔150s对轴向位移和扭转角度进行记录，以反映试样不同方向上的参量变化。图6是不同等效应力幅下的加载曲线。如图6(a)所示，随着等效应力幅的增大，轴向位移幅值整体有增加的趋势；不同的等效应力幅下，在加载初始阶段，轴向位移幅值均随时间增加，材料在该阶段轴向出现软化现象，其后轴向位移幅值随时间出现波浪形变化，材料轴向的硬化和软化交替出现；对于高应力幅条件，材料轴向主要以软化为主，寿命较短，对于低应力幅条件，由于轴向出现了多次硬化过程，对应寿命较长。如图6(b)所示，随着等效应力幅的增大，扭向角度幅值整体有增加的趋势；在350MPa高应力幅条件下，在初始阶段软化-硬化过程后，扭向角度幅值逐渐增加，材料在扭向出现持续软化现象，对应寿命最低；在250MPa低应力幅条件下，材料扭向的硬化和软化交替出现，直至断裂。

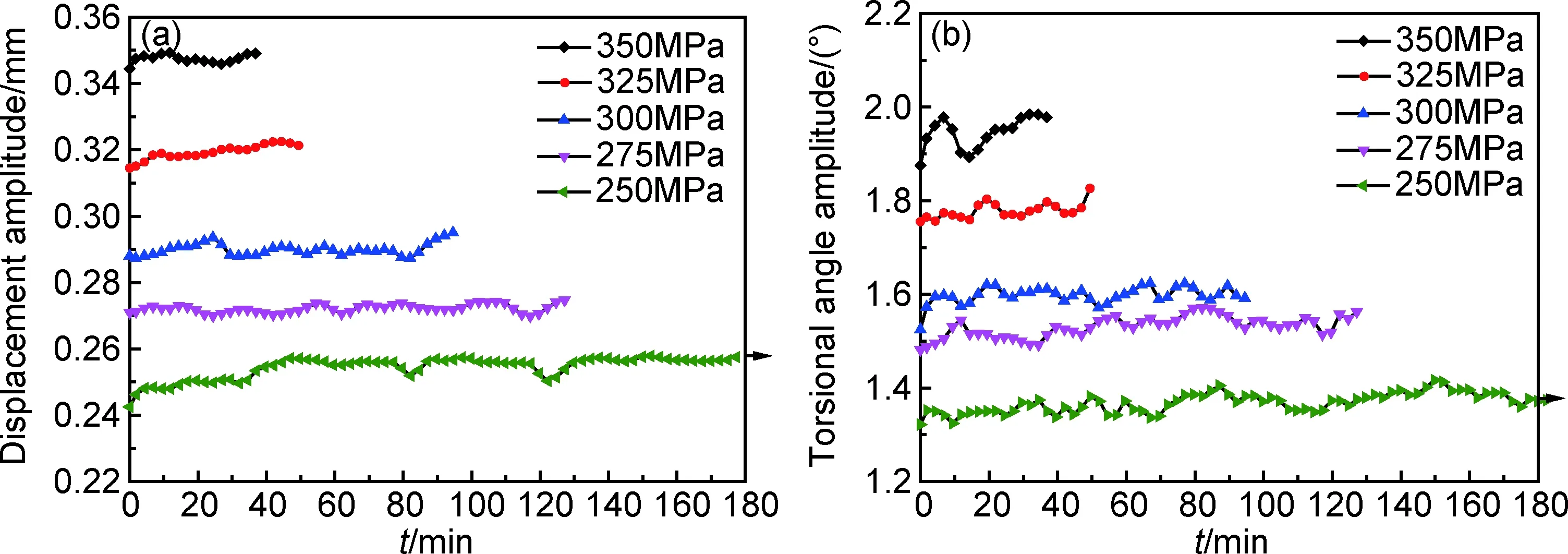
图6 应力幅比λ为相位差φ为0°时不同等效应力幅下的加载曲线(a)轴向位移幅值随时间的变化；(b)扭向角度幅值随时间的变化Fig.6 Loading curves under different equivalent stress amplitudes with and φ= 0° (a)variation of axial displacement amplitude with time;(b)variation of torsional angle amplitude with time

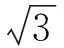
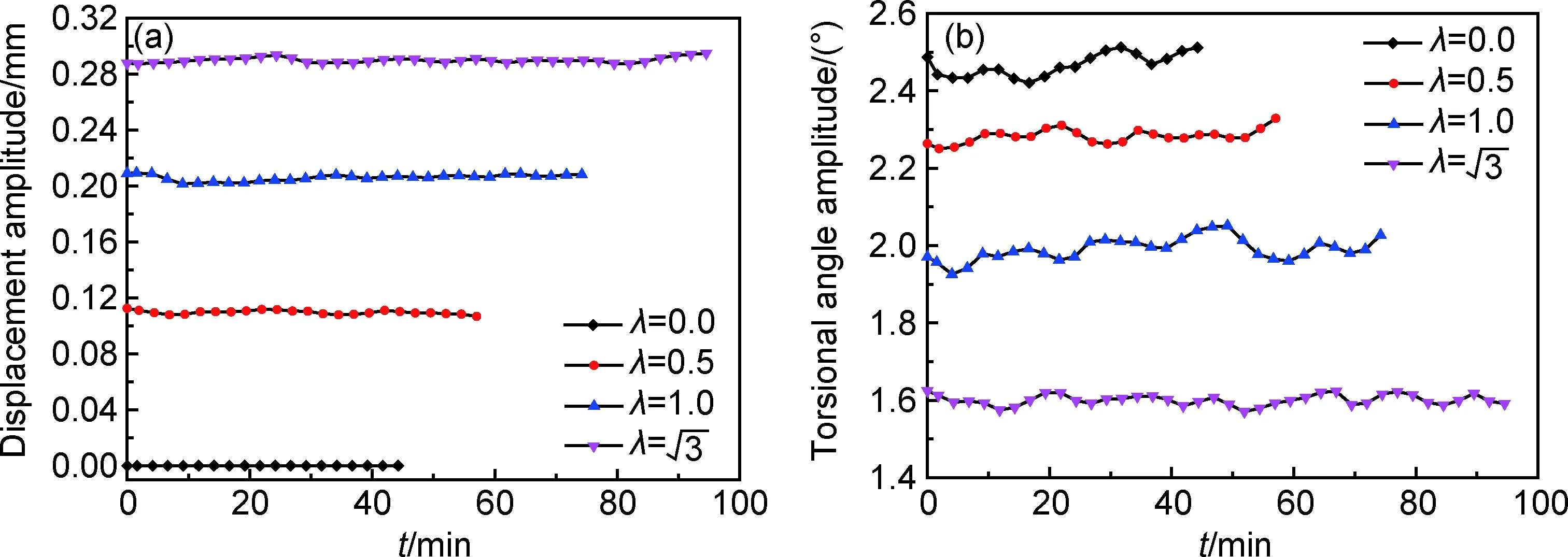
图7 等效应力幅σeq为300MPa、相位差φ为0°时不同应力幅比下的加载曲线(a)轴向位移幅值随时间的变化；(b)扭向角度幅值随时间的变化Fig.7 Loading curves under different stress amplitude ratios with σeq=300MPa and φ= 0° (a)variation of axial displacement amplitude with time;(b)variation of torsional angle amplitude with time

2.2 断口形貌分析

2.2.1 等效应力幅变量实验

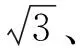
2.2.2 应力幅比变量实验

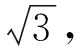
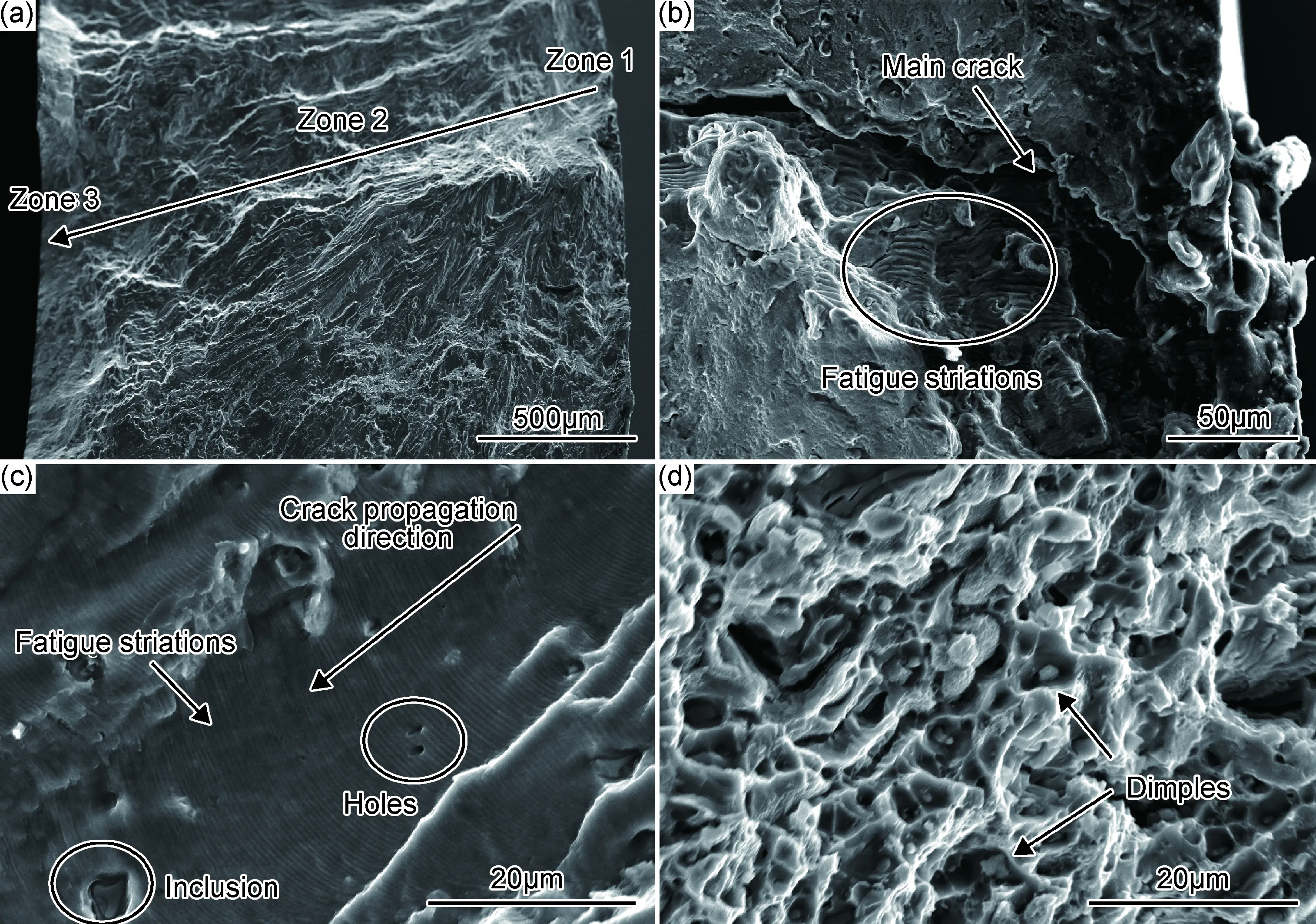
图8 250MPa等效应力幅下试样断口宏观和微观形貌a)宏观断口；(b)裂纹源区；(c)裂纹扩展区；(d)瞬断区Fig.8 Macro and micro fracture morphologies of specimen under equivalent stress amplitude of 250MPa (a)macro fracture;(b)crack initiation region;(c)crack propagation region;(d)instantaneous fracture region

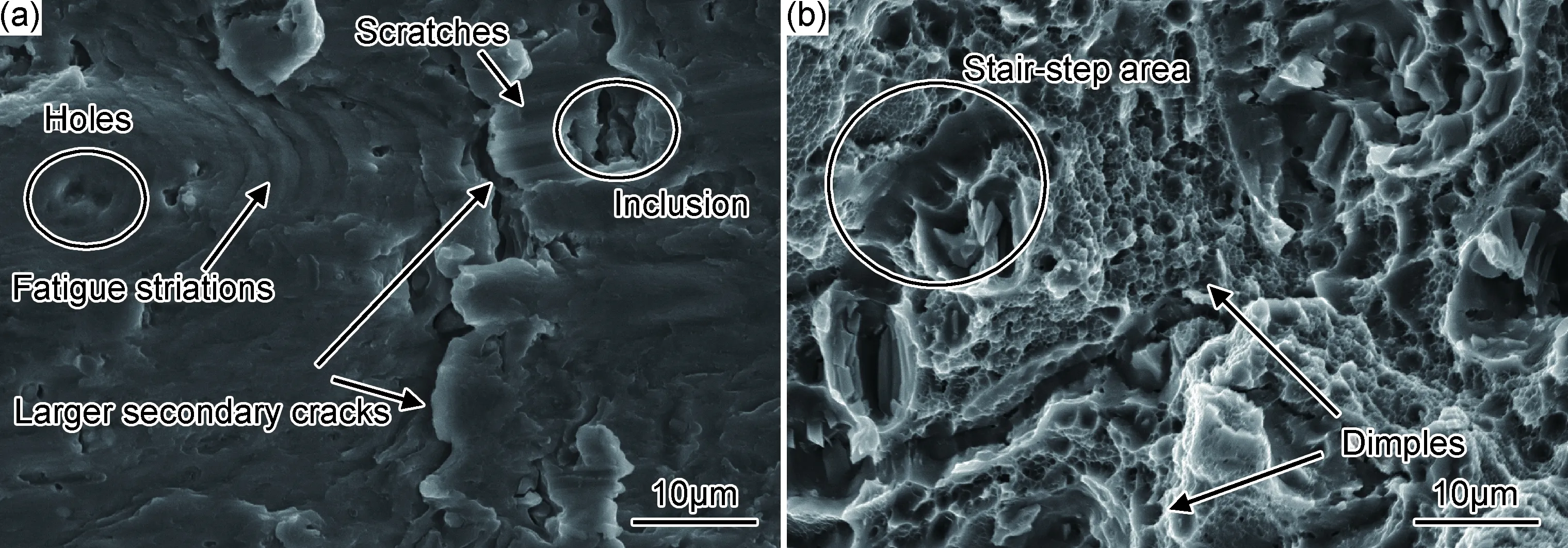
图9 350MPa等效应力幅下试样断口微观形貌(a)裂纹扩展区；(b)瞬断区Fig.9 Fracture morphologies of specimen under equivalent stress amplitude of 350MPa (a)crack propagation region;(b)instantaneous fracture region

图10 不同应力幅比下试样断口宏观特征(从左至右：Fig.10 Macro fracture of specimens under different stress amplitude ratios (from left to right:

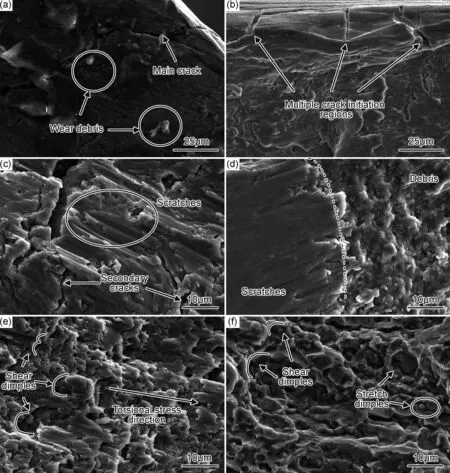
图11 不同应力幅比下断口微观形貌(a)疲劳源区(λ=0)；(b)疲劳源区扩展区(λ=0)；(d)扩展区瞬断区(λ=0)；(f)瞬断区Fig.11 Fracture morphology under different stress amplitude ratios (a)crack initiation region (λ=0)；(b)crack initiation region propagation region (λ=0)；(d)crack propagation region fracture region (λ=0)；(f)instantaneous fracture region

3 多轴疲劳寿命预测

考虑到拉扭相位差在多轴低周疲劳条件下对材料疲劳寿命的影响较小，下面仅针对等效应力幅和应力幅比两个变量对材料的多轴疲劳寿命的影响进行预测。

3.1 等效应力幅对寿命的影响

Basquin[32]针对单轴疲劳的寿命预测，提出了正应力幅和疲劳寿命之间的关系：

(4)

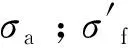
(5)

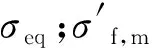
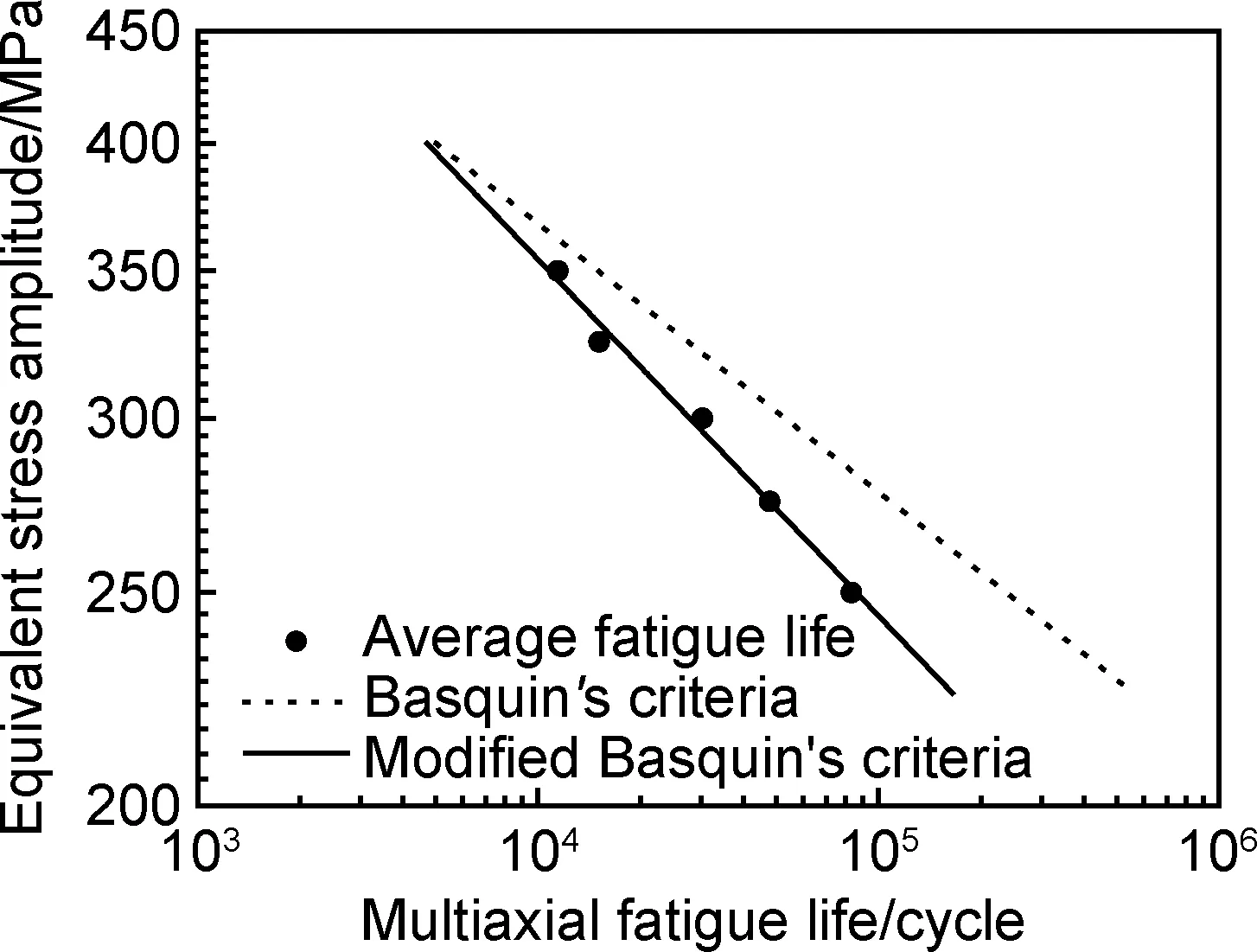
图12 原始Baquin准则和修正后准则的对比Fig.12 Comparison between original and modified Basquin’s criteria

3.2 应力幅比对寿命的影响

考虑应力幅比在等效应力恒定情况下对多轴疲劳寿命的影响，引入应力幅比因子μ，式(5)可写作：

(6)

应力幅比因子μ是应力幅比λ的函数，当应力幅比λ升高时，多轴疲劳寿命增加，而应力幅比因子应减小，具体关系如下：

(7)

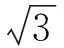
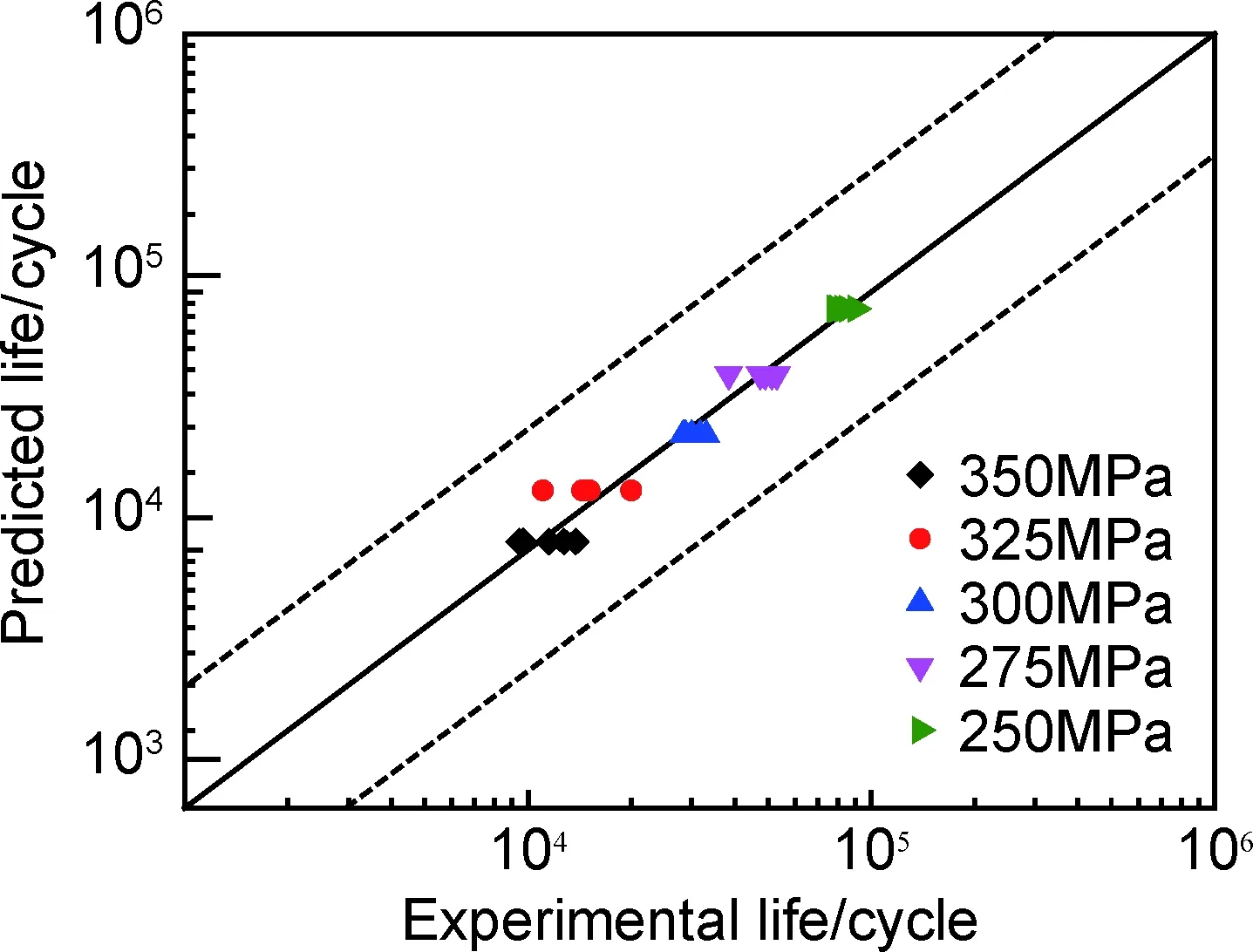
图13 不同等效应力幅条件下寿命预测结果Fig.13 Life prediction results under different equivalent stress amplitudes

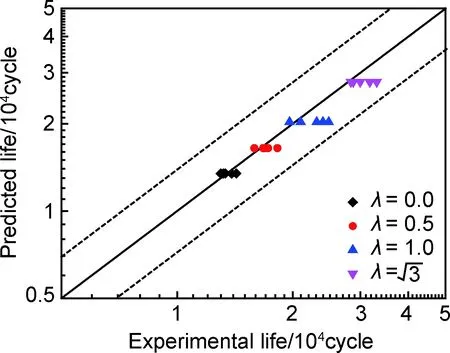
图14 不同应力幅比条件下寿命预测结果Fig.14 Life prediction results under different stress amplitude ratios

4 结论

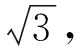
(2)不同加载条件下，裂纹源均位于管壁外侧，且呈现多裂纹源特征。低应力幅下扩展区可观察到密集的疲劳条带，瞬断区韧窝方向和深度不同；高应力幅下扩展区出现脱落颗粒并形成沟槽，瞬断区出现台阶状形貌。试样宏观断口在纯扭转条件下出现平台区域，随着应力幅比的增加，平台区域逐渐减小。较低应力幅比下，扩展区主要以擦痕和犁沟为主，且可以观察到二次裂纹；较高应力幅比下，扩展区出现较多碎屑。随着应力幅比的增加，瞬断区出现的韧窝呈现由剪切型到拉伸和剪切混合型的过渡。

(3)针对多轴加载条件，通过引入应力幅比因子，得到修正的Basquin准则，呈现出良好的寿命预测效果，所得寿命预测值均在两倍分散带以内。